M×M X信道与基本信道并存网络的自由度
王希超,刘 锋,郭倩倩,曾连荪
(上海海事大学 信息工程学院,上海 201306)
M×M X信道与基本信道并存网络的自由度
王希超,刘 锋,郭倩倩,曾连荪
(上海海事大学 信息工程学院,上海 201306)
研究了在各节点已知全局信道状态信息(Channel State Information,CSI)时,由M×MX信道(X Channel,XC)和基本信道构成的并存网络的自由度。此处基本信道涉及两种类型:点对点信道(Point to Point, PTP)、M用户广播信道(Broadcast Channel,BC)。XC每个发送端给每个接收端发送期望消息,BC只给对应接收端发送独立消息。基于符号扩展模型,通过分M个时隙讨论,在每个时隙采用渐进干扰对齐方案得到了M×MXC分别与上述两种基本信道并存网络的自由度下界。另一方面,该下界也被证明是自由度上界,故得出几种并存网络系统的自由度。
自由度;并存信道;符号扩展;渐进干扰对齐
0 引言
与单输入单输出系统相比,多输入多输出(Multiple Input Multiple Output,MIMO)系统[1-2]的容量有了很大的改善。根据自由度与信道容量公式C(SNR)=dlog(SNR)+o(log(SNR))可知,在高信噪比(Signal Noise Ratio,SNR)下,o(log(SNR))是log(SNR)的高阶无穷小,可以忽略,信道容量可用自由度近似线性表征。因此,可以通过研究自由度来替代研究信道容量,以规避从信息论本身出发研究信道容量的困难。
多输入多输出技术是从天线分集技术和智能天线技术演变而来,包含了两种技术的优势。上世纪末,由贝尔实验室E.Telatar与J.Foshini证明了MIMO系统比较于之前的MISO和SIMO两个通信系统,系统信道容量有明显的提高[3-5]。
国内外对于单个网络单个信道的理论研究已经非常成熟,而对于一般更复杂的多网络或多个信道并存网络的研究才刚刚开始。文献[6]针对两个BC共存时的自由度进行了研究。通过迫零方法得到两个小区相互干扰的K用户BC网络的自由度为d=min(2M,2KN,max(M,N),其中两个小区内的基站天线配置为M,小区内移动台的天线配置为N。推广到一般情况,文献[7]将两个小区扩展到多个小区互相干扰的BC自由度分析。对于两个PTP共存、PTP与BC共存以及基本信道与IC共存网络的研究,通过线性干扰对齐技术分析均有相应的结论。
1 系统模型

HM+1,M+1(k)VpkXpk+Zj(k))
(1)
其中,Yj(k)为第k个时隙第j个接收端的输出信号,k∈{1,2,…,M},j∈{1,2,…,M+1};Hj,i(k)表示第k个时隙从发送端i到接收端j的信道矩阵;Xl⊕(k-1),l和Xpk表示第k个时隙主信道和次信道发送的消息,它们对应的波束成形向量分别用Vl⊕(k-1),l和Vpk表示;Zj(k)为第k个时隙第j个接收端的噪声。

图1 M×M XC与PTP并存系数模型

HM+k,M+1VM+k,M+1XM+k,M+1+Zj(k)
(2)

图2 M×M XC与BC并存网络模型
2 M×M XC和PTP并存网络的自由度
2.1自由度下界
图1网络中的主信道XC发送M2个消息,次信道PTP发送1个消息。将PTP发送的消息分成M个独立的符号,用Xpk{k∈1,2,…,M}表示次信道PTP第k个时隙发送的符号。将所有M(M+1)个符号平均分配到M个时隙中发送,在第k个时隙发送的符号为Xl⊕(k-1),l(发送端l到接收端l⊕(k-1)的消息,l∈{1,2,…,M})和Xpk。若考虑M个时隙中的某一个时隙,则每个时隙相当于一个M+1用户干扰信道IC,如图3所示以第1个时隙为例证明自由度下界。为了便于描述,将第一个时隙的信道矩阵Hj,i(1)简记为Hj,i。

图3 第1个时隙收发消息示意图
定理1:M×MXC与PTP共存的网络模型,在M个时隙内总共可获得的自由度为dXC+dPTP=(M+1)/2。
证明:采用干扰对齐方案:
图3所示在接收端1,采用完美干扰对齐,将来自发送端2到发送端M+1的所有干扰消息与来自PTP发送端的消息完美对齐,约束关系如下式:
H1,2V2,2=H1,3V3,3=…=H1,MVM,M=H1,M+1VP1
(3)
在接收端k(k>1)采用渐进干扰对齐,将来自其他发送端的所有干扰渐进对齐到来自发送端1的干扰所在的空间维度上,得到如下约束关系:
(4)

(5)
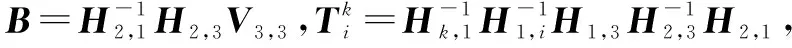
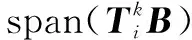
(6)
其中,k,i∈{2,3,…,M+1},k≠i。令w=[1 … 1 1]T是Mn,1×1的列向量。从下面的集合中选择B、V1,1,从而满足式(6)约束关系。

(7)
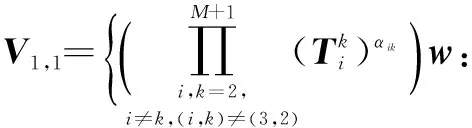
(8)
要保证期望信号空间和干扰信号空间不重叠,需证明每个接收端的期望信号空间和干扰信号空间是满秩的。
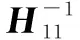
(9)
其中αk∈{0,1,2,…,n},βk∈{0,1,2,…,n-1},dl来自一个连续的分布。用反证法证明S是满秩的,即只需推出P(det(S)=0)>0不成立。
将矩阵S按第一行展开得到其行列式为:

(10)
其中,Cm,n表示矩阵S中第m行第n列元素的代数余子式。如果λ1k,β1k的值给定,那么S=0必将导致下面所述条件之一:
(1)d1是此方程的根;
(2)λ1k、β1k的各次乘积项系数都等于0。
由于d1来自于一个连续的分布,所以满足上述条件(1)的概率几乎为零,下面只需要证明满足上述条件(2)的概率大于零即可。即式(11)成立的概率大于零。
C1,(n+1)N+1+λ11C1,(n+1)N+2+…+
(11)
接下来考虑式(11),同理必将满足下面所述条件之一:
(1)λ1k是此方程的根;
(2)λ1k的各次乘积项系数都等于0。
满足上述条件(1)的概率几乎为零,故只需证明满足上述条件(2)的概率大于零。由此可推出其中一个充分条件是P(C1,(n+1)N+nN=0)>0。然后,通过第一行最后一列元素的代数余子式等于零构造一个方程,重复以上步骤Mn,1-1次后会推出矛盾。不失一般性,可假设w在第一列,则会推出“1=0”的矛盾。同理,在其他时隙采用相同方法,又因为系统总的自由度等于每个时隙的自由度相加再除以时隙数,所以每个时隙的自由度就等于系统总的自由度。
通过上述讨论可以得到M×M用户XC与PTP并存时的自由度为:dXC+dPTP=(M+1)/2。
2.2自由度上界
已知K用户IC自由度外界为K/2,本节研究的并存信道模型上界推导分M个时隙考虑,即M(M+1)个符号分M个时隙发送。在第i个时隙发送的符号为Xi⊕(M-1),i和Xpi,共发送M+1个符号,这样每时隙信道模型可以等价为一个M+1用户IC。所以每一个时隙发送消息的自由度上界为(M+1)/2,M(M+1)个符号在M个时隙内自由度上界为M(M+1)/2M=(M+1)/2。
由此可得,M×MXC与PTP并存网络模型可达到自由度上界(M+1)/2,即自由度上下界是紧的。
3 M×M XC与BC并存网络的自由度
3.1自由度下界
由图2所示主网XC发送M2个消息,次网BC发送M个消息。在第k个时隙发送的消息为Xl⊕(k-1),l和XM+k,M+1,l∈{1,2,…,M}。同理这里以第1个时隙为例证明自由度下界。同样,为了便于描述,信道矩阵Hj,i(1)简记为Hj,i。
定理2:M×MXC与M用户BC并存的网络模型,在M个时隙内总共可获得的自由度为:
证明:采用干扰对齐方案
在接收端1,采用完美干扰对齐将发送端2到发送端M+1的干扰消息完美对齐,约束关系如下:
H1,2V2,2=H1,3V3,3…H1,MVM,M=H1,M+1VB1
(12)
在接收端k(k>1)采用渐进干扰对齐,将来自其他发送端的干扰(除去来自发送端1的干扰外有M-1个干扰)渐进对齐到来自发送端1的干扰所在的空间维度上,得到如下约束关系:
(13)
这样每个接收端共有M-1个约束关系。与M×MXC与PTP并存同理,由式(12)和式(13)可得到:
(14)

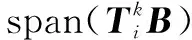
(15)
其中,k,i∈{2,3,…,M+1},k≠i。令w=[1 … 1 1]T都是Mn,1×1的列向量。从下面的集合中选择B、V1,1,从而满足式(15)。

(16)

(17)
与M×MXC和PTP并存网路模型对比,接收端信号空间矩阵是相同的。满秩证明与M×MXC和PTP并存网络相同。
3.2自由度上界
已知K用户IC自由度外界为K/2,本节研究的并存信道模型上界推导分M个时隙考虑,即M(M+1)个消息分M个时隙发送。每一个时隙发送M+1个消息,这样每个时隙的信道模型可以等价为一个M+1用户的IC。所以每一个时隙发送消息的自由度上界为(M+1)/2,M(M+1)个消息在M个时隙内自由度上界为(M+1)/2,此上界与自由度下界是紧的。
4 结束语
本文对M×MXC与基本信道(PTP,BC)并存时网络的自由度做了有关分析。首先分析了M×MXC与PTP共存网络模型的自由度下界和上界,其次研究了M×MXC与M用户BC共存时的自由度下界和上界。通过分析可知,本文所提出的干扰对齐方案可以使这两种并存网络模型的自由度下界与推导的自由度上界相等,即系统模型的自由度达到了(M+1)/2。
[1] BIGLIERI E,CALDERBANK R, CONSTANTINIDES A, et al. MIMO wireless communications[M].Cambridge University Press, 2007.
[2] 李韶华,王有政,周祖成. MIMO-OFDM中基于波束成形的天线选择研究[J]. 微计算机信息,2007,23(6):99-101.
[3] FOSCHINI G J,GANS M J. On limits of wireless communication in a fading environment when using multiple antennas[J].Wireless Personal Communications,1998,6(3):311-335.
[4] TELATAR I E. Capacity of multi-antenna Gaussian channels[J]. Bell Labs Tech MIMO, 1999,10(6): 585-595.
[5] CARLEIAL A. A case where interference dose not reduce capacity (corresp.) [J].IEEE Transactions on Information Theory, 1975, 21(5):569-570.
[6] KIM J, PARK S H, SUNG H, et al. Sum rate analysis of two-cell MIMO broadcast channels: spatial amultiplexing again[C].Proceedings of the Communications(ICC), 2010 IEEE International Conference on, IEEE, 2010: 1-5.
[7] SRIDHARAN G, YU W. Degrees of freedom of MIMO cellular networks: decomposition an dalinear beamforming design[J]. IEEE Transactions on Information Theory,2015,61(6):3339-3364.
王希超(1992-),男,硕士研究生,主要研究方向:MIMO。
刘锋(1976-),通讯作者,男,博士,副教授,主要研究方向:无线通信。
郭倩倩(1990-),女,硕士研究生,主要研究方向:MIMO。
贸泽开售Maxim MAX30004生物电势模拟前端助力可穿戴医疗,随时为健康把关
2017年8月29日-专注于新产品引入 (NPI) 并提供极丰富产品类型的业界顶级半导体和电子元器件分销商贸泽电子(Mouser Electronics)即日起开售 Maxim Integrated的 MAX30004 生物电势模拟前端(AFE)。MAX30004 AFE是针对可穿戴医疗应用的单通道生物电势心率监测AFE解决方案,可用于心率胸带和单导联无线心率贴片等产品,在剧烈运动时,无需在微控制器中提取和处理心电图(ECG)数据。
贸泽电子供应的Maxim MAX30004 AFE提供单个生物电势通道来测量心跳的 R-R波间距以确定心率。此生物电势通道提供静电放电(ESD)保护、电磁干扰(EMI)滤波和DC导联脱落检测。MAX30004为内置的自测功能提供广泛的校准电压,并且其软上电顺序可以确保没有大的瞬态信号注入电极。
MAX30004的全差分输入结构提供超过100 dB的高共模抑制比(CMRR)和超过500 MΩ的高阻抗,提高了共模到差模的转换能力。0.7 mA的导联开通功能允许AFE的微控制器保持深度睡眠模式,同时让实时时钟关闭,直至检测到有效的导联条件为止。可配置的中断允许微控制器仅在每次心跳时唤醒,从而降低了整体系统功耗。
(贸泽电子 供稿)
DoF of coexisting network with M×M X channel and the basic channel
Wang Xichao, Liu Feng, Guo Qianqian, Zeng Liansun
(College of Information Engineering, Shanghai Maritime University, Shanghai 201306, China)
This paper studied the degrees of freedom (DoF) for coexisting network composed byM×MX channel and basic channel with global channel state information (CSI) at each node. Here basic channel includes two types: point to point (PTP) andM-user broadcast channel (BC). Based on symbol extension model, we explore the asymptotic interference alignment approach to obtain the lower bound on the DoF of the coexisting network withM×MXC and the above two types of basic channels, respectively. On the other hand, this lower bound is proved to be the upper bound on DoF, so the DoF of the discussed coexisting networks is obtained.
degrees of freedom; coexisting channel; symbol extension; asymptotic interference alignment
TN929.5
:A
10.19358/j.issn.1674- 7720.2017.17.021
王希超,刘锋,郭倩倩,等.M×MX信道与基本信道并存网络的自由度[J].微型机与应用,2017,36(17):71-74,78.
2017-01-14)

