基于双噪声耦合技术的连续时间Sigma-Delta ADC设计

邓建飞，严海月，林福江

(中国科学技术大学 信息科学技术学院，安徽 合肥 230026)

基于双噪声耦合技术的连续时间Sigma-Delta ADC设计

邓建飞，严海月，林福江

(中国科学技术大学 信息科学技术学院，安徽 合肥 230026)

连续时间Sigma-Delta调制器被大量应用于音频电子系统及其他领域。设计采用单环二阶连续时间系统架构，包含分段式7 bit Flash量化器，提出了双噪声耦合结构。通过对系统结构的改进，二阶系统有很好的稳定性，能实现三阶的噪声整形效果，对DAC失配、环路延时、放大器有限带宽等非理想特性有着非常好的鲁棒性。仿真结果显示，在3 M的输入信号带宽，16倍的过采样率时，调制器信噪失真比(SNDR)达到96.9 dB,有效比特数(ENOB)为15.8 bit，输入信号动态范围(DR)为98 dB。

连续时间Sigma-Delta 调制器；双噪声耦合；分段式量化器

0 引言

目前，SAR ADC、Pipeline ADC和Sigma-Delta ADC是三种主流的模数转换器[1]，然而，SAR ADC因为比较器的噪声限制[2-3]，12 bit以上的精度实现起来相当困难，Pipeline ADC噪声被级间放大器逐级放大，一般能够实现的有效精度只有不到8 bit，随着现代音频系统、测量系统等对精度要求的提高，Sigma-Delta ADC逐渐成为研究的热门[4]。

然而，离散时间的Sigma-Delta ADC因为采用开关电容积分器，电容的充放电时间严重地限制了输入信号的信号带宽，连续时间架构采用 RC积分器，可以完美地解决带宽问题[5-7]，而且连续架构自带抗混叠滤波器，减小了一部分电路开销。当然，连续时间Sigma-Delta ADC也面临一些挑战：时钟抖动和环路延时对系统稳定性有一定影响，反馈DAC的失配也会影响系统的性能。

本文在数字滤波结构的基础上，创造性地提出了双噪声耦合结构，极大地提高了系统性能。

1 系统建模

连续时间Sigma-Delta ADC主要采用噪声整形技术和过采样技术。一般而言，环路滤波器的阶数越高，噪声整形效果越好，然而，当环路架构超过三阶时，系统的稳定性会急剧下降，系统的输入摆幅也会因此受到严重限制，多环路级联结构又会因为级间匹配性差而难以实现。所以如何在不影响系统稳定性的前提下提高噪声整形的阶数是设计的难点。另一方面，高OSR限制了量化器的位数，同时也限制了信号带宽，所以OSR和量化器位数也需要权衡。

综合考虑以上因素，本文采用二阶单环架构，过采样率为16，采用7 bit量化器，如图1所示。为了降低积分器输出摆幅，从而降低放大器的设计难度，节省功耗，加入了前馈通路。根据脉冲不变响应[8]和参数转换法[9]，连续系统传输方程可以由离散系统进行推导：

Y1(n)=STF(z)U(z)+NTF(z)E(z)

(1)

其中Y(n)表示数字输出，U(z)表示输入模拟信号，E(z)是量化噪声，STF(z)是信号传递函数，NTF(z)是噪声传递函数。根据系统推导得到：

STF(z)≃1； NTF(z)=(1-z-1)2

(2)

即系统对于信号是全通函数，而对于噪声是二阶高通函数，从而实现了噪声整形效果。

图1 单环二阶连续系统

1.1数字滤波技术

在单环二阶系统中，为了提高系统的转换精度，本文采用了7 bit的Flash量化器，然而这会导致环路反馈DAC的失配变得非常严重，针对该问题，采用了数字滤波技术[10]，如图2所示。

图2 数字滤波架构

图4 双噪声耦合架构

7 bit量化器被分成4 bit MSB和3 bit LSB两个部分，其中MSB部分依然反馈回环路滤波器，而LSB部分则通过与模拟滤波器匹配的数字滤波器来达到同样的滤波效果。数字滤波结构传输方程如下：

Y2(n)=Y1(n)+LSB(NTF(z)-

NTF(z)digital)

(3)

数字滤波器与模拟滤波器相匹配时，传输方程与式(1)结果一致，此时反馈DAC由7 bit减少到4 bit，DAC的失配减弱，输出信号谐波失真被极大地抑制，系统性能得到很大提高。

1.2数字噪声耦合技术

然而在实际中，由于受环路滤波器的影响，模拟滤波器和数字滤波器一般不能完美匹配，这会使得有一小部分噪声泄露出来。为了解决噪声泄露带来的影响，本文提出了数字噪声耦合技术。如图3所示。

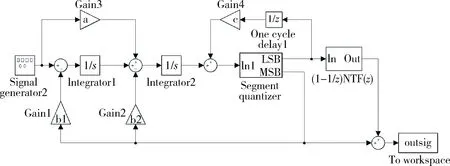
图3 数字噪声耦合架构

LSB经过一个采样周期的延时后重新送回到量化器的输入端，数字滤波器同时增加一阶，此时的系统传输方程中噪声泄露项为：

Y3(n)=Y1(n)+Δleak

(4)

Δleak=ΔmismatchLSB·(1-z-1)

(5)

可以看到，滤波器不匹配带来的噪声泄露乘以一个(1-1/z)的高通函数,相当于泄露的噪声有了一阶噪声整形效果，虽然比系统的二阶整形效果低了一阶，但是考虑到泄露噪声的能量本来就不高，所以仍然可以达到很好的效果。

1.3自噪声耦合技术

一般而言，在Sigma-Delta ADC中，噪声整形效果由环路滤波器阶数决定，其他手段都在解决系统非理想因素带来的影响。由于滤波器增加一阶滤波器需要付出的代价太大，所以考虑在量化器处增加一阶噪声整形，基于该思路本文提出双噪声耦合结构，在数字噪声耦合结构的基础上增加了自噪声耦合环路，构成了双噪声耦合结构，如图4所示。

将量化自身的量化噪声延迟一个周期后耦合到量化器输入端。系统传递函数为：

Y4(n)=STF(z)U(z)+(1-z-1)NTF(z)E(z)+Δleak

(6)

可以看出，噪声传递函数增加了(1-1/z)这样一个高通函数，相当于量化器获得了一阶噪声整形效果，这使得系统噪声性能提升一阶。需要特别指出的是，自噪声耦合环路反馈了所有的7 bit量化器输出，如果有一路存在DAC失配的问题，但是，该路被包含在两阶的环路滤波器中，所以DAC非线性误差会有两阶噪声整形效果，因此即使这一路没有数字滤波，失配依然不足以影响系统精度。另外，自噪声环路LSB部分也被送入模拟滤波环路，所以数字滤波器不用额外再增加一阶。图5显示了几种结构的性能对比，从图中可以看出，双噪声整形技术有效地提升了系统性能。

图5 噪声性能对比

2 系统性能分析

系统性能会受到其他的非理想因素影响，本节主要对系统性能作进一步分析，DAC失配问题已经通过系统设计得到很好的解决，因此主要需要考虑由积分器有限带宽、环路延时与时钟抖动和输入信号的幅值带来的影响。

2.1积分器有限带宽与有限增益

本设计采用的是RC积分器，主要非理想因素是积分器的有限带宽和有限增益。对于有限增益，因为系统的速度不是非常快，而且加入了前馈系统，所以对于增益的要求并不高，系统计算后，只需要放大器开环增益大于50 dB即可，这样一个增益要求很容易达到。相比而言，带宽影响占主要地位，由文献[11]可知，有限带宽的积分器传递函数可以表示为：

ITFGBWi=

(7)

其中i表示第i路反馈，k表示积分器反馈通路的增益因子，当运放的开环增益足够大时，式(7)可化简为：

(8)

其中：

(9)

(10)

由式(8)可以看出，带宽有限的积分器可以等效成一个理想积分器乘以一个增益误差和一个额外的积分器延时，增益误差可以通过调节RC常数解决。而根据文献[12]可以计算出本文系统带来的额外延时为0.05个采样周期，该延时带来的影响在下文中会进行讨论。

2.2环路延时与时钟抖动

在高速电路中，时钟抖动带来的影响会很大，而本文结构只有80 MHz的采样频率，时钟抖动的影响基本可以忽略。本文采用的分段式Flash量化器，其量化延时在0.08个采样周期以内，而积分器的延时通过计算在0.05个采样周期左右，因此系统环路延时大约在0.13个采样周期，图6体现了环路延时对系统SNDR的影响，可以看出，当环路总延时低于0.3个采样周期时，系统性能基本不会有太大衰减。

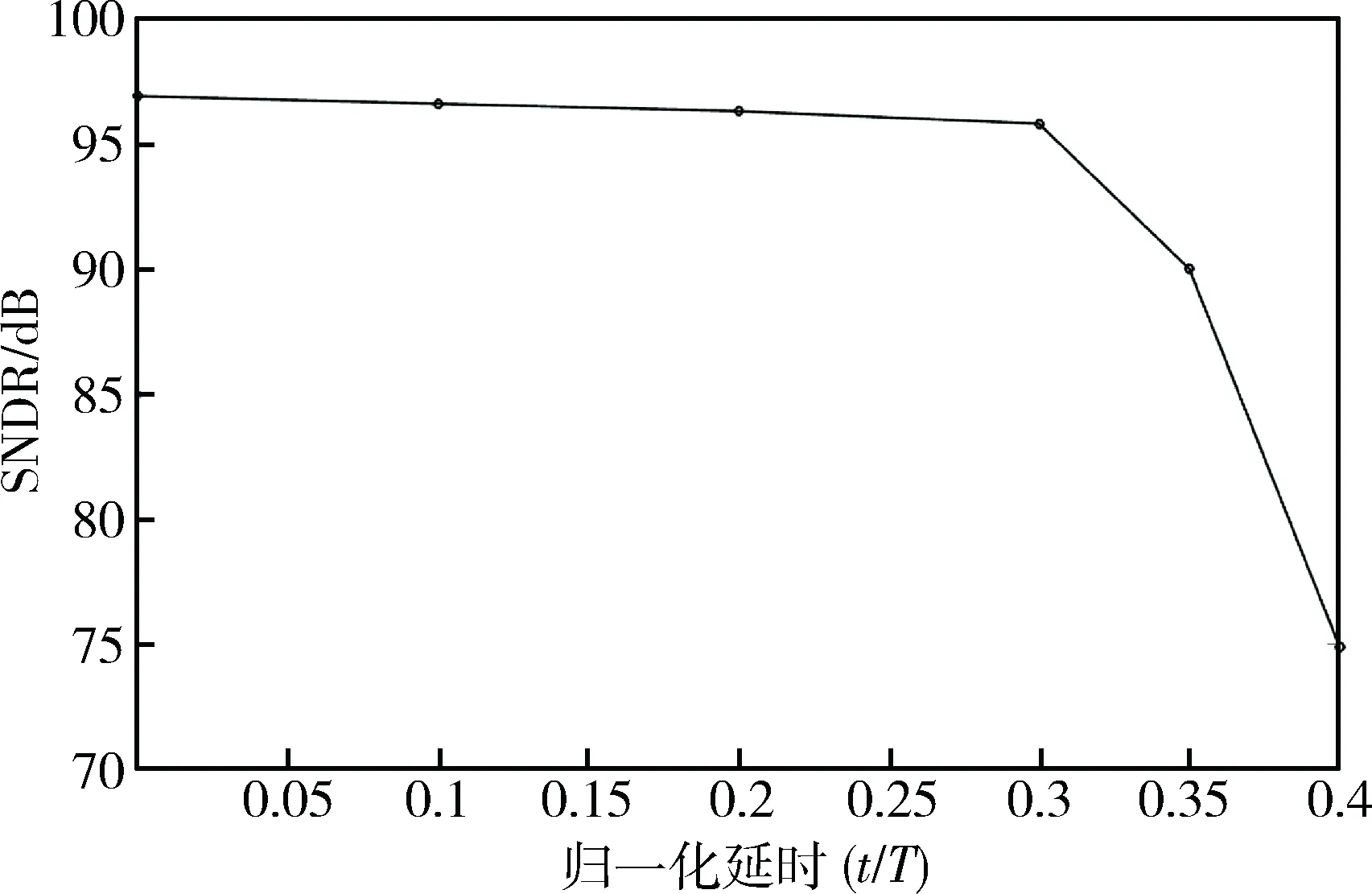
图6 环路延时对系统性能的影响

2.3输入动态范围

动态范围(Dynamic Range, DR)指的是最大信号功率和最小信号功率的比值，最小信号指的是SNDR为0 dB时的输入信号功率，即能检测到的最小输入信号。DR是ADC重要的指标之一，通过系统仿真，本设计的输入信号幅值与SNDR之间的关系如图7所示。

图7 输入信号幅值与SNDR的关系

由图7可以看出，输入动态范围为98 dB，系统有非常好的线性度。

3 结论

双噪声耦合技术很好地解决了噪声泄露的问题，并构造了具有噪声整形效果的量化器,在3 MB的信号带宽内，系统可以达到98 dB的动态范围和96.9 dB的SNDR,具有非常好的稳定性与线性度，且该技术具有良好的移植性，对Sigma-Delta ADC设计有一定借鉴意义。后续会就提高系统速率和降低系统功耗做进一步研究。

[1] MURMANN B. ADC performance survey 1997-2016[EB/OL].(2016-07-12)[2016-12-16]. Available:http://web.stanford.edu/～murmann/adcsurvey.html.

[2] 徐韦佳,施琴,田俊杰,等. 一种应用于10位SAR ADC的高精度比较器电路设计[J]. 微型机与应用,2017,36(4):32-35.

[3] 赵川,唐宁,翟江辉. 用于SAR ADC中的双通道逐次逼近寄存器的设计与实现[J]. 微型机与应用,2015,34(10):25-28.

[4] 郭红转. 一种数字陀螺中∑-△DAC的数字调制器设计和验证[J]. 电子技术应用,2015,41(4):53-55,59.

[5] SCHREIER R, ZHANG B. Delta-sigma modulators employing continuous-time circuitry[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1996, 43(4): 324-332.

[6] ORTMANNS M, GERFERS F, MANOLI Y. A continuous-time sigma-delta modulator with switched capacitor controlled current mode feedback[C]. Proceedings of the 29th European Solid-State Circuits Conference, 2003. IEEE, 2003: 249-252.

[7] KAUFFMAN J G, WITTE P, LEHMANN M, et al. A 72 db dr, ct ΔΣ modulator using digitally estimated, auxiliary dac linearization achieving 88 fj/conv-step in a 25 MHz bw[J]. IEEE Journal of Solid-State Circuits, 2014, 49(2): 392-404.

[8] GERFERS F, ORTMANNS M. Continuous-time sigma-delta A/D conversion: fundamentals, performance limits and robust implementations[M]. Springer Science & Business Media, 2006.

[9] MARQUES A, PELUSO V, STEYAERT M S, et al. Optimal parameters ΔΣ modulator topologies[J]. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 1998, 45(9): 1232-1241.

[10] LEE C C, ALPMAN E, WEAVER S, et al. A 66 dB SND 15 MHz BW SAR assisted ΔΣ ADC in 22nm tri-gate CMOS[C]. VLSI Circuits (VLSIC), 2013 Symposium on. IEEE, 2013: 64-65.

[11] ORTMANNS M, GERFERS F, MANOLI Y. Compensation of finite gain-bandwidth induced errors in continuous-time sigma-delta modulators[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(6): 1088-1099.

[12] KELLER M, BUHMANN A, SAUERBREY J, et al. A comparative study on excess-loop-delay compensation techniques for continuous-time sigma-delta modulators[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(11): 3480-3487.

Design of continuous-time Sigma-Delta ADC based on double noise coupling technology

Deng Jianfei, Yan Haiyue, Lin Fujiang

(School of Information Science and Technology, University of Science and Technology of China, Hefei 230026, China)

Continuous-time Sigma-Delta modulators are widely used in audio electronics and other applications. This paper adopts the single-ring second-order continuous-time system architecture, including a 7 bit segmented Flash quantizer, and proposes a double-noise coupling structure. The system can achieve the third-order noise shaping effect with a good stability, and has a quite good robustness to DAC mismatch, loop delay, amplifier bandwidth and other non-ideal characteristics. The simulation results show that the output Signal to Noise and Distortion Ratio(SNDR) of the modulator reaches 96.9 dB and the Effective Number of Bits(ENOB)is 15.8 bit when the input signal bandwidth is 3M and OverSamping Rate(OSR) is 16，and the dynamic range of input signal reaches 98 dB.

continues-time Sigma-Delta mudulators; double-noise coupling; segmented quantizer

TN431

：A

10.19358/j.issn.1674- 7720.2017.17.008

邓建飞，严海月，林福江.基于双噪声耦合技术的连续时间Sigma-Delta ADC设计[J].微型机与应用，2017,36(17)：27-30.

2017-03-12)

邓建飞(1991-)，通信作者，男，硕士研究生，主要研究方向：模拟集成电路设计。E-mail:jianfeid@mail.ustc.edu.cn。