机械转向器冲击试验台建模与仿真

陈云朋，麦云飞

(上海理工大学 机械工程学院，上海 200093)

机械转向器冲击试验台建模与仿真

陈云朋，麦云飞

(上海理工大学 机械工程学院，上海 200093)

EPS用机械转向器是实现汽车转向的主要部件之一，为保证车辆的安全性，需要了解其耐冲击性能。机械转向器冲击试验台主要用于对机械转向器的冲击试验。文中针对试验台的阀控非对称缸电液力控制系统进行了研究。通过对控制系统的各个环节的分析，建立各环节的数学模型。进而得到以力为控制量的电液伺服系统数学模型，并利用Simulink仿真平台对系统进行频域和时域分析。分析结果表明，试验台液压系统闭环稳定,满足性能要求。

冲击实验台；阀控非对称缸；电液力控制；Simulink仿真

电动助力转向器EPS(Electric Power Steering System)是助力转向器的一种，传统的助力转向还包括HPS液压助力转向[1]。EPS用机械转向器是汽车转向总成的重要部件。在实际应用中，机械转向器有可能会受到短暂的纵向剧烈冲击，从而造成机械转向器的功能失效。机械转向器冲击试验台用于在测试机械转向器的抗冲击性能。液压伺服控制系统是实现试验加载并保证加载力动态品质的关键环节[2]。试验台的液压系统为电液力控制系统，要求液压系统在输入控制信号后，能够快速的达到并稳定在设定压力。

本文主要针对电液力控制系统建立数学模型，并在Simulink仿真平台对控制系统模型进行时域和频域的仿真分析，进而分析系统的稳定性及其性能。

1 试验台电液力系统的控原理

机械转向器冲击试验台液压系统主要由伺服放大器、电液伺服阀、非对称液压缸及力传感器组成，其原理如图1所示。

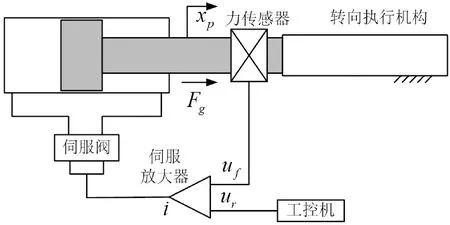
图1 试验台电液力控制系统

控制系统实现了力的闭环控制，其控制原理如下：当力控制信号ur与力传感器的反馈信号uf不等时，伺服放大器输出偏差电流i，控制电液伺服阀，进而电液伺服阀输出流量和压力，推动液压缸输出液压力Fg，液压缸的输出力Fg又作用在机械转向器上；当传感器的反馈信号与输入力信号相等时，输出力Fg被控制在某一希望的输出力上[3]。

2 电液力控制系统数学建模

2.1 阀控非对称缸的建模

2.1.1 阀控非对称缸的工作原理

非对称缸相对于对称缸来说具有体积小、结构简单、承载能力大等优点，在工程中应用广泛[4]。冲击试验需要较大加载力。同等条件下，非对成缸较对称缸更能产生大的加载力。对称阀控制非对称缸的液压系统的工作原理如图2所示。

图2 阀控非对称缸原理图

图2中，A1，A2为无杆腔和有杆腔活塞作用面积；p1，p2为无杆腔和有杆腔的压力；q1,q2为进出液压缸的流量；ps为供油压力；p0为回油压力；pL为负载压力；Cip为液压缸内泄漏系数；Cep为液压缸外泄漏系数；mt为负载质量；K为负载弹簧刚度；Bp为负载粘性阻尼系数；xv为阀芯位移；xp为活塞杆位移。

2.1.2 基本定义

在推导阀控非对称液压缸的基本方程之前，需做以下定义[5-6]：液压缸两腔活塞有效作用面积比

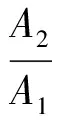
(1)

负载压力

pL=p1-np2

(2)

负载流量

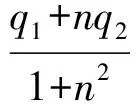
(3)

2.1.3 阀控非对称缸的基本方程

非对称缸活塞两侧面积不等,描述其正反向工作油路的数学模型也不同[7]。但本文所分析的是电液力控制系统，根据实际工况，只需分析活塞杆伸出的情况,以保证加载力不会丢失。因此本文仅在在活塞伸出方向上对阀控非对称缸的基本方程进行分析。

(1) 滑阀的流量方程。假设阀是零开口四边滑阀，4个节流窗口是匹配和对称的，供油压力ps恒定，回油压力p0为零。则阀的流量方程为

qL=Kqxv-KcpL

(4)

式中，Kq为伺服阀流量增益系数；Kc为伺服阀流量-压力系数；

(2) 液压缸的流量连续性方程[8-9]。流入液压缸无杆腔的流量q1为

(5)

流出液压缸有杆腔腔的流量q2为

(6)

式中，V1和V2为液压缸无、有杆腔的容积；βe为液压油弹性模量。

液压缸工作缸的容积可写为

V1=V10-A1xp

(7)

V2=V20-A2xp

(8)

式中，V10和V20为 液压缸无、有杆腔的初始容积。

在分析时，取使液压缸左右两腔初始容积相等的活塞位置作为初始位置。则有

(9)

式中，V0为初始容积；Vt为总压缩容积。因A1xp，A2xp≪V0故忽略不计。

由式(5)～式(9)可得液压缸的流量连续性方程为

(10)

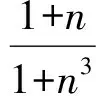
(3)液压缸和负载的力平衡方程。在本电液伺服系统中，由于活塞杆与负载固联，故负载力包括惯性力、粘性阻尼力和弹性力。则液压缸的输出力与负载力的平衡方程为

(11)

式中，Fg为液压缸输出力。

对式(4)，式(10)和式(11)进行拉普拉斯变换可得

QL=KqXv-KcPL

(12)

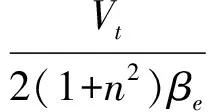
(13)

Fg=mts2Xp+BpsXp+KXp

(14)

2.2 伺服放大器的数学模型

因为伺服放大器的频宽较大，可将该环节视为比例环节。其传递函数为

ΔI=Ka(Ur-Uf)

(15)

式中，ΔI为放大器输出电流；Ka为放大器增益系数；Ur为系统设定输入电压；Uf为力传感器的输出反馈电压。

2.3 电液伺服阀的数学模型

本文选用的电液伺服阀是美国MOOG G761-3005。其主要参数：负载流量63 L/min；最大工作压力31.5 MPa；压降7 MPa；内泄漏2.4 L/min，额定电流40 mA。系统中执行元件固有频率低于50 Hz,伺服阀的传递函数可用一阶环节表示，即[10]

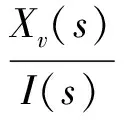
(16)

式中，I为伺服阀输入电流；Ksv为伺服阀增益系数；Tsv为伺服阀时间常数。

2.4 力传感器的数学模型

一般情况下，力传感器的频带都比系统固有频宽大得多，故传感器模型可以近似为比例环节，其传递函数可表示为

Uf=KfFFg

(17)

式中，Uf为传感器输出电压；KfF为传感器反馈增益系数；Fg为液压缸输出力。

2.5 系统结构框图的建立

根据式(12)～式(17)可得本系统框图如图3所示。

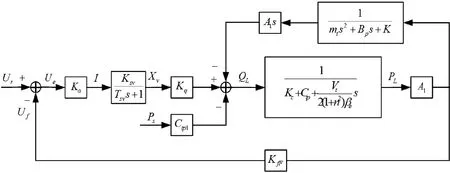
图3 力控制系统方框图

3 系统仿真与分析

稳定性是伺服系统的重要特性，因此，液压伺服系统的动态分析和设计是以稳定性要求为中心进行的[11]。而液压系统动态特性的研究方法主要有：传递函数分析法、实验研究法、模拟仿真法和数字仿真的方法[12]。本文采用仿真研究液压系统的动态特性，分析其稳定性及性能。

3.1 仿真模型的建立

近年来Matlab/Simulink在控制系统仿真、分析得到了广泛的应用[13]。Simulink可以方便地对系统进行建模、仿真与分析，从而使一个复杂模型的建立和仿真变得相当简单和直观[14]。本文利用Simulink仿真平台对本文建立的模型进行仿真与分析，系统参数如表1所示。

表1 力控制系统仿真参数

根据图3可绘出Simulink仿真模型如图4所示。

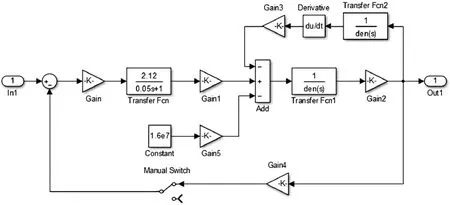
图4 力控制系统Simulink仿真模型

3.2 系统仿真结果分析

通过Simulink仿真，可得到系统的频域特性曲线和时域特性曲线，如图5和图6所示。

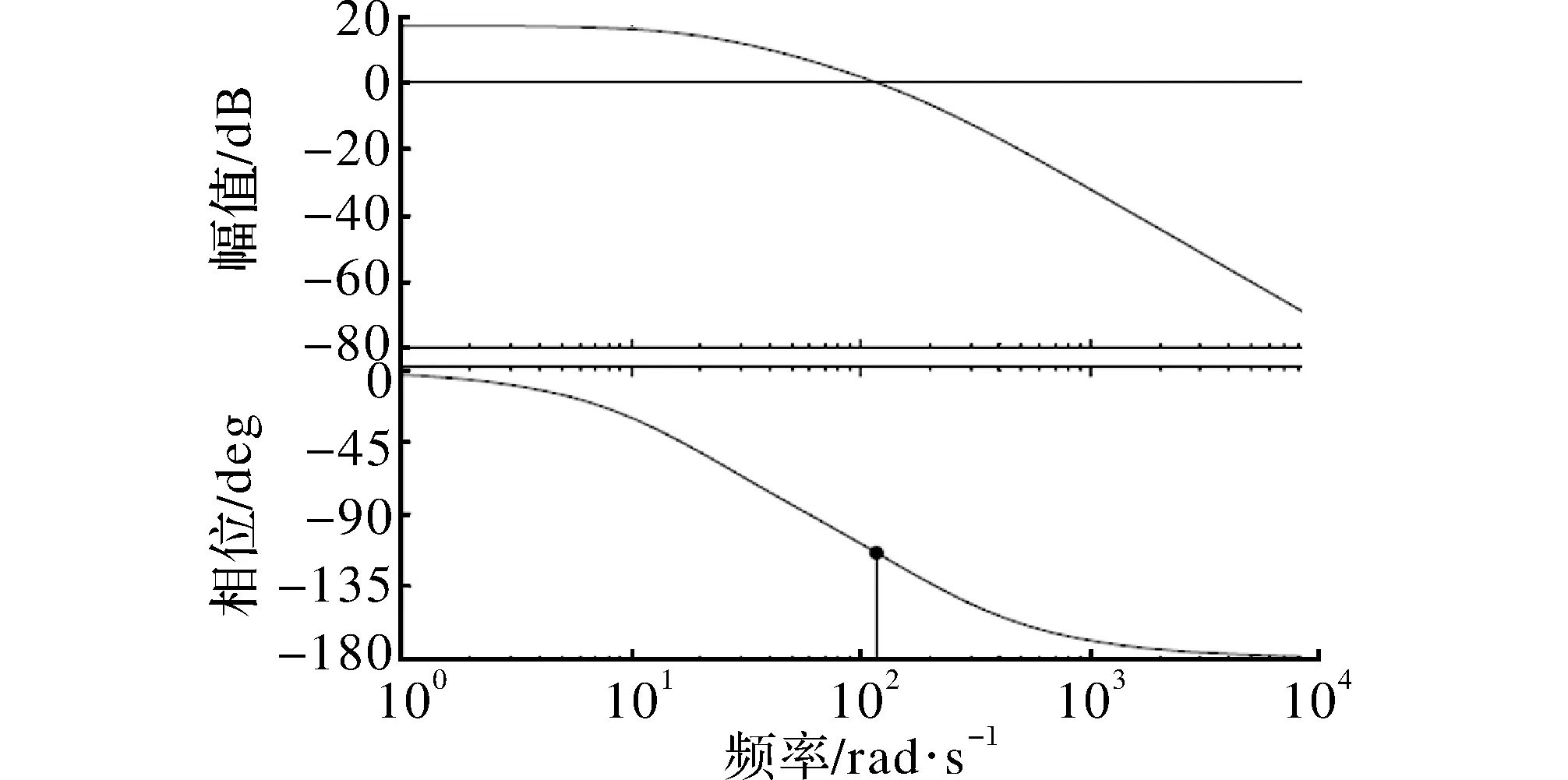
图5 力控制系统开环频率特性

图6 力控制系统时域阶跃响应曲线

由图5可知，幅值穿越频率ωc=117 Hz。本系统的开环系统为最小相位系统。若开环对数幅频特性达到0 dB时，其对数相频特性仍>-180°线，即相位不足-180°，则闭环系统稳定[15]。因此本系统是闭环稳定的。

由图6可知，本系统主要的时域性能指标为：最大超调量10.8%；调整时间0.034 9 s。由此可得系统的时域特性满足工程需要。

4 结束语

针对汽车转向器冲击试验台的电液伺服力控制系统建立了数学模型，并利Simulink对数学模型进行了仿真，对该系统进行了频域特性和时域特性分析。结果表明，本系统是闭环稳定的，其调整时间满足对系统响应快速性的要求。本文的研究对试验台的设计具有一定的理论参考价值，但是系统也存在超调的问题，后续可对此进行更深入的研究和优化，进而提高系统性能。

[1] Shriwastava.Electric power steering with permanent magnet synchronous motor drive used in automotive application [C].Passadina:2011 1st International Conference on Electrical Energy Systems,2011.

[2] 陈立群.疲劳试验台的液压伺服控制研究[D].合肥:合肥工业大学,2012.

[3] 吴振顺. 液压控制系统[M]. 北京:高等教育出版,2008.

[4] 叶小华,岑豫皖,赵韩,等.基于液压弹簧刚度的阀控非对称缸建模仿真[J].中国机械工程,2011(22):23-27.

[5] 汪首坤,彭建敏.带遗忘因子的预测迭代学习控制在阀控非对称缸系统中的应用研究[J].机械工程学报,2014,50(10):191-198.

[6] 王占林.近代电气液压伺服控制[M].北京:北京航空航天大学出版社,2005.

[7] 吕云篙.阀控非对称缸频域建模[J].机械工程学报,2007,43(9):122-125.

[8] 王春行. 液压伺服控制系统系统[M]. 北京:机械工业出版社,1999.

[9] 张晓明.42MPa电液伺服压力脉冲试验机的设计与研究[D]. 秦皇岛:燕山大学,2013.

[10] 刘丹丹,骆艳洁,麦云飞. EPS疲劳试验台电液位置建模与仿真[J]. 通用电源技术,2015,32(5):87-89.

[11] 李洪人.液压控制系统[M].北京: 国防工业出版社,1981.

[12] 李永堂,雷步芳,高雨茁.液压系统建模与仿真[M]. 北京:冶金工业出版社,2003.

[13] 宋志安,张鑫,宋玉凤,等.Matlab/Simulink机电系统建模与仿真[M].北京:国防工业出版社,2015.

[14] 宋志安.基于Matlab的液压伺服控制系统分析与设计[M].北京:国防工业出版社,2007.

[15] 杨叔子,杨克冲,吴波,等. 机械工程控制基础[M]. 武汉：华中科技大学出版社,2001.

Modeling and Simulation of Mechanical Steering Gear Impact Tester

CHEN Yunpeng，MAI Yunfei

(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

the mechanical steering gear of EPS is one of the main parts of the automotive steering assembly, in order to guarantee the safety of the vehicle, it is necessary to understand its impact resistance performance. The mechanical steering gear impact tester is mainly used for the impact test of the mechanical steering gear. For the valve controlled asymmetric cylinder electro hydraulic servo force control system used in the impact tester was studied. Through the analysis of all components of the control system, establishing their mathematical models. Then got the mathematical model of the electric hydraulic servo system who regarded force as the control object. And the system was analyzed in frequency domain and time domain by using the Simulink simulation platform. Analysis indicated that the hydraulic closed-loop system is stable and can meet the performance requirements.

impact test machine; valve controlled asymmetric cylinder; force servo control; Simulink simulation

2016- 09- 25

陈云朋(1987-)，男，硕士研究生。研究方向：电液伺服控制。

10.16180/j.cnki.issn1007-7820.2017.09.033

TN911.72;TH871.4

A

1007-7820(2017)09-122-04