基于脉冲压缩的高频超声信号实时增强系统

姜旭恒，郑 政，胡胜男

(上海理工大学 医疗器械与食品学院，上海 200093)

基于脉冲压缩的高频超声信号实时增强系统

姜旭恒，郑 政，胡胜男

(上海理工大学 医疗器械与食品学院，上海 200093)

高频超声成像具有高分辨率的优点，但其衰减速度过快导致探测深度过浅。编码脉冲压缩可以解决高频超声纵向分辨率和探测深度的矛盾。利用FPGA设计了一个线性调频脉冲的发射和实时压缩系统，通过发射大时宽-带宽积的线性调频脉冲来保证信号的能量,从而提高探测深度，在接收端通过脉冲压缩获得窄脉冲保证分辨率。实验表明，中心频率为10 MHz和50 MHz的高频超声回波信号，经过脉冲压缩以后的分辨率分别为0.3 mm和41 μm，旁瓣水平分别为48 dB和37 dB，信噪比分别提高15 dB和10 dB。

高频超声;编码脉冲压缩;线性调频脉冲;现场可编程门阵列;信噪比

超声成像的分辨率与探查深度之间相互制约。由于超声衰减系数和频率成正比，高频超声的衰减尤其显著，而超声发射声压受到医学安全标准的限制，所以提高回波能量需要延长超声脉冲的持续时间，显然这将导致纵向分辨能力的下降[1]。编码脉冲压缩可以在保证分辨率的前提下显著提高信噪比，从而改善分辨率和探查深度之间的矛盾[2-11]。线性调频信号的产生和处理均较容易，其脉冲压缩的形状和信噪比对多普勒频移不敏感，且技术成熟，所以采用线性调频信号作为发射脉冲[5]。以此为出发点设计了线性调频脉冲的发射和实时压缩系统，该系统可以满足临床常用的10 MHz、20 MHz和50 MHz等高频超声信号的实时处理要求。

1 线性调频信号的脉冲压缩原理

在实际系统中，脉冲压缩既可以在时域实现，也可以在频域实现。线性调频脉冲压缩实质上就是对回波进行频率延时，信号的起始频率部分延迟时间长，终止频率部分延迟时间短，这样可以保证调频信号的不同频率分量几乎同时从压缩网络输出，经过延时后形成窄脉冲[12]。

1.1 线性调频信号

射频信号的线性调频脉冲可以表示为

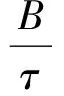
(1)

其复数表达式为

(2)

其中，A是信号幅度；f0是信号的中心频率；τ是脉宽；B是频带宽度。

该波形的瞬时频率fi(t)是相位函数的微分。很明显，在τ的脉宽内fi(t)线性地扫过了整个带宽B

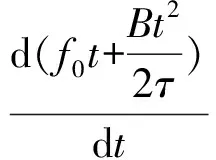
(3)

1.2 匹配滤波器

脉冲压缩滤波器是一个匹配滤波器，这是一种最大信噪比滤波器，当信号和噪声叠加在一起输入该系统时，匹配滤波使信号成分在某一瞬时出现峰值，而噪声成分受到抑制，即使输出的信噪比最大。

匹配滤波器的冲激响应可以表示为

h(t)=Φ×(τ-t)

(4)

它是激励信号的共轭、翻转并时移。匹配滤波器的输出表达式为

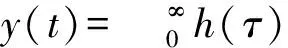
(5)

1.3 基带处理

将超声回波信号变换到基带并降采样后进行处理可以显著节省硬件资源，提高处理速度[6]。并且文献[7]证明8倍降采样后的基带脉冲压缩处理引入的误差为-36.8 dB，而4倍降采样的误差为-49 dB[7]。对于实际的系统，这样的误差已经能够满足要求。

设本地振荡器输出信号

zi(t)=cos2πf0t，0≤t≤τ

(6)

zq(t)=sin2πf0t，0≤t≤τ

(7)

射频回波信号s(t)与本地振荡器进行混频(IQ解调)

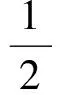
(8)

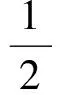
(9)

经过低通滤波以后得到基带复信号

(10)

其频域表达式为

(11)

匹配滤波器的频域表达式为

(12)

其中，td0为脉冲压缩网络的固定时延。匹配滤波器的频域输出表达式为

U(ω)=Y(ω)×H(ω)=|Y(ω)|2e-jωtd0

(13)

1.4 旁瓣抑制

具有矩形包络的线性调频信号通过匹配滤波后的波形具有sinc函数的形状，旁瓣高度为-13 dB。距离旁瓣的存在是有害的，大目标的距离旁瓣往往会压制附近小目标的主瓣，导致小目标检测不到。为此，需要旁瓣抑制技术来尽可能降低旁瓣高度。根据频谱分析，矩形包络的线性调频信号的频谱上带有菲涅尔波纹，该波纹会导致远端旁瓣的产生。对线性调频信号幅度加权Lanczos窗[11]可以有效的抑制远端旁瓣。同时对匹配滤波器加权切比雪夫窗[11]可以有效的抑制近端旁瓣。

2 系统设计

线性调频脉冲的发射和压缩系统框图如图1所示。线同步信号作为整个系统的控制信号。线性调频信号数据通过串口配置到FPGA中，在FPGA中与Lanczos窗加权后由数模转换器DAC转换为模拟信号经功率放大器、Expander后作用于换能器。回波信号经过Limiter、回波放大电路后由模数转换器ADC采集进入FPGA，进行脉冲压缩处理，脉冲压缩后的数字信号一路通过JTAG与PC端通信，便于从Signaltap软件观察数据，另一路通过数模转换器DAC连接到示波器便于实时观察。对于10 MHz中心频率的超声信号采样频率为50 MHz，对于50 MHz中心频率的超声信号采样频率为200 MHz，采样点数均为4 096点。电路中所使用的FPGA为Altera公司的CycloneV系列，ADC和DAC的精度为14 bit，最大采集速度为250 MHz。

图1 线性调频脉冲发射和压缩系统

射频回波信号s(n)经模数转换器ADC采集进入FPGA，由于射频信号的频率较高，过带通滤波器后进行IQ解调并降采样成为基带复信号，然后对其做快速傅里叶变换FFT，并与存在ROM中的失配滤波器参数相乘，将相乘后的结果做快速逆傅里叶变换IFFT，通过包络检测得到脉冲压缩结果。系统对不同中心频率超声信号的采集、处理参数如表1所示。

表1 不同中心频率超声信号的采集、处理参数

系统需要满足不同中心频率高频超声的实时脉冲压缩处理，而FPGA本身无法辨别信号的中心频率，如果不对信号中心频率和FPGA之间建立某种协议的话，将会导致后续脉冲压缩算法出错，所以如何准确的识别不同的超声中心频率成为系统设计的重要环节。上文中提到线性调频脉冲数据是由上位机配置到FPGA中，所以在每一帧线性调频脉冲数据之前都会加上一个8位二进制的帧头，即超声中心频率选择信号，不同中心频率超声对应不同的帧头，帧头数据通过串口配置到FPGA中，FPGA中的译码器模块会对上位机传来的数据进行译码，识别出频率选择信号和线性调频信号，并将频率选择信号分别送到脉冲发射模块控制数模转换器DAC的工作时钟，送到采集控制电路控制模数转换器ADC的工作时钟以及送到脉冲压缩模块控制IQ解调和失配滤波器模块中ROM的地址。通过此方法可以准确的识别不同中心频率的超声信号，在不改变脉冲压缩模块的情况下可以对不同中心频率的超声信号进行实时脉冲压缩处理。

3 实验结果与分析

3.1 实验设计

系统分别针对10 MHz和50 MHz换能器进行了实验。如图1所示，PC将配置参数写入FPGA，由脉冲发射电路输出线性调频脉冲，经过DAC后用射频功率放大器(BBA150)放大，经Expander激励换能器。回波信号经Limiter后由小信号射频放大器放大。脉冲压缩算法在数字域中实现，利用FPGA设计软件Quartus II中的SignalTap[13-15]在线调试和评估脉冲压缩效果。同时，为了方便实时观察靶线回波位置以及压缩结果，将包络检测后的压缩结果通过数模转换器DAC转换成模拟信号后连接到示波器做实时观察。

针对10 MHz换能器的线性调频脉冲频率为7～13 MHz，实验目标为两根平行靶线构成的线靶，两根靶线间距为6 mm。

针对50 MHz换能器的线性调频脉冲频率为35～65 MHz，实验目标为水层厚度为50 μm的层靶。

3.2 实验结果

图2分别为10 MHz超声和50 MHz超声的脉冲压缩实验结果示意图。

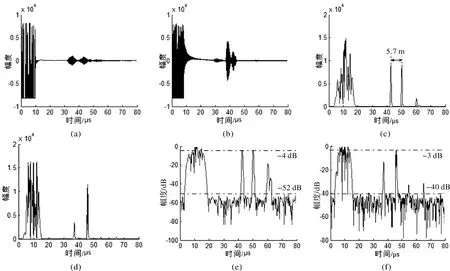
图2 脉冲压缩实验结果及靶目标示意图

10 MHz换能器的靶线回波和脉冲压缩结果如图2(a)和2(b)所示。图中横坐标表示回波的长度，纵坐标表示信号幅度。原始回波信号的信噪比为33 dB，从图2(c)中可以观察到，脉冲压缩后信噪比可达48 dB以上，至少提高了15 dB。如图2(b)所示，根据超声在水中的声速[16]计算得到两根靶线之间的距离为5.7 mm，与实际距离相比误差为5%。其-3 dB脉宽的纵向分辨力为0.3 mm，对应脉宽为400 ns，与10 MHz单脉冲纵向分辨力相当。

50 MHz换能器的层靶回波与脉冲压缩结果以及信噪比情况如图2(d)、图2(e)和图2(f)所示。原始回波信号的信噪比为27 dB，脉冲压缩后信噪比在37 dB以上，提升了10 dB以上。由于两片有机玻璃相隔较近，实际距离仅为50 μm，所以其前壁和后壁的实际回波混叠在一起难以辨别。通过脉冲压缩以后则可以区分两个目标，根据时间换算可知两壁之间的距离为56 μm，与实际距离相比误差为12%，其-3 dB脉宽的纵向分辨力为41 μm，对应脉宽为55 ns，与50 MHz单脉冲纵向分辨力相当。

4 结束语

利用FPGA实现了基于脉冲压缩的高频超声信号的实时增强系统，在满足浅表器官B型超声扫描仪的实时性需求的同时，可以较大的提升回波信号的信噪比。实际超声回波信号的包络呈梭型，这是发射端功率放大器和回波放大器的非线性以及超声换能器的频带特性共同作用的结果，可以使用线性度更佳的放大器以及频带特性更好的超声换能器来提高原始回波的质量，从而可以使脉冲压缩后信噪比的改善[17]以及旁瓣抑制效果更佳。

[1] 周浩,王友钊,郑音飞.医学超声编码激励技术研究进展[J].浙江大学学报:工学报,2011,45(2):387-391.

[2] Takeuchi Y.An investigation of a spread energy method for medical ultrasound systems.Part one: theory and investigation[J].Ultrasonics,1979,17(4):175-182.

[3] O’Donnell M.Coded excitation system for improving the penetration of real-time phased-array imaging systems[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1992,39(3):341-351.

[4] Rao N A.Investigation of a pulse compression technique for medical ultrasound: a simulation study[J].Medical & Biological Engineering & Computing,1994,32(2):181-188.

[5] 董亚清.基于GPU的线性调频信号脉冲压缩算法实现[J].电子科技,2013,26(12):12-16.

[6] Kolumban G,Krebesz T L,Lau F C M,et al.Theory and application of software defined electronics: design concepts for the next generation of telecommunications and measurement systems[J].IEEE Circuits and Systems Magazine,2012,12(2):8-34.

[7] Yoon C,Lee W,Chang J,et al.An efficient pulse compression method of chirp-coded excitation in medical ultrasound imaging[J].IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,2013,60(10):2225-2229.

[8] Misaridis T,Jensen J A.Use of modulated excitation signals in medical ultrasound. PartII: design and performance for medical imaging applications[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,2005,52(2):192-207.

[9] Misaridis T,Jensen J A.Use of modulated excitation signals in medical ultrasound. Part iii: high frame rate imaging[J].IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,2005,52(2):208-219.

[10] Jensen J A.Field: a program for simulating ultrasound systems[J].Medical & Biological Engineering & Computing,1996,34(6):351-353.

[11] Behar V, Adam D.Parameter optimization of pulse compression in ultrasound imaging systems with coded excitation[J].Ultrasonics,2004,42(10):1101-1109.

[12] 翟庆林,张军,付强.线性调频脉冲压缩技术及其在雷达系统中的应用[J].现代电子技术,2007,30(1):17-19.

[13] 王诚. Altera FPGA CPLD设计[M].北京:人民邮电出版社,2005.

[14] 刘可,徐伯庆,孙国强.基于FPGA的电子提花机控制系统[J].上海理工大学学报,2004,26(2):168-171.

[15] 蒋念平,李伟.现场可编程门阵列实现液晶显示控制的新方法[J].上海理工大学学报,2009,31(2):190-194.

[16] 冯若.超声诊断设备原理与设计[M].北京:中国医药科技出版社,1993.

[17] Machado T,Costa E.A comparative study using both coded excitation and conventional pulses in the evaluation of signal to noise ratio sensitivity and axial resolution in ultrasonic A-mode scan[J].Brazilian Journal of Medical Physics,2011,5(1):35-40.

The System of High Frequency Ultrasonic Signal Real-time Enhancement Based on Pulse Compression

JIANG Xuheng，ZHENG Zheng，HU Shengnan

(School of Medical Instrumentation and Food Engineering,University of Shanghai for Science & Technology, Shanghai 200093,China)

The high frequency ultrasound imaging has the advantage of high resolution, but it attenuates too fast to detect more information.The coding pulse compression can solve the contradiction between the resolution and the detection depth of high frequency ultrasound. A real-time compression and transmission system of chirp is designed by using field programmable gate array (FPGA),it will enlarge the signal energy to improve detection depth by transmitting a large time-bandwidth product’s(TBP) chirp,and narrow pulse guarantee resolution is obtained by pulse compression at the receiving end. The experimental results show that the resolution of the high frequency ultrasonic echo signals with center frequency of 10 MHz and 50 MHz are 0.3 mm and 41 μm after pulse compression, respectively. The sidelobe level is 48 dB and 37 dB respectively, and the SNR is increased by 15 dB and 10 dB, respectively.

high frequency ultrasonic; coding pulse compression; chirp; FPGA; signal to noise ratio

2016- 11- 28

姜旭恒(1991-)，男，硕士研究生。研究方向：医学超声成像。郑政(1961-)，男，博士，研究员。研究方向：超声影像等。

10.16180/j.cnki.issn1007-7820.2017.09.003

TN911.2;R445

A

1007-7820(2017)09-008-04