套管井井液中超声场的三维可视化数值模拟

安正林，周 武

(东北石油大学 地球科学学院，黑龙江 大庆 163318)

0 前 言

超声测井技术广泛应用于工程地质勘探行业。其理论基础为超声波检测理论，该理论建立在介质中弹性波的传播理论上，以人工激振向介质发生超声波，同时在一定的空间距离上接受介质物理特性调制的声波并进行分析，进而解决岩土工程问题[1-2]。但超声换能器的形状、工作频率、井孔大小等因素对超声波的衰减有一定的影响，导致超声测井图像对比度低、细节模糊。

沈永进用贝塞尔方程求解了套管井中二维声场的声场特性[3]。吕加利用三维应力—速度有限差分方法数值模拟了井孔中的声场[4]。秦正贵采用实轴积分方法研究了套管井井口声场[5]。胡文祥利用数值计算得出了套管井声场的声压模型[6]。这些研究为超声测井提供了理论基础，但是这些研究的模型都是在过井轴的二维平面上计算超声波的分布，很少有人在套管井的三维空间内进行超声场的运算。

套管井内的超声接受器接收到的声场是由套管井壁壁面反射回来的超声波，仅从二维平面内进行计算超声波的分布会带来很大的误差，不利于超声测井技术的改进与优化。本文利用COMSOL软件实现了套管井中超声场的三维可视化仿真，得出套管内的超声场声压等值面，导出井轴上的声压级分布曲线，同时通过数值计算结果的对比，旨在为更加精确、图像对比度更高的的超声波测井技术提供理论基础。

1 超声测井原理与理论模型

实际油井井眼及周围情况较为复杂，为了分析实际问题而建立的物理模型只能近似的模拟井下情况。本文研究井外介质厚度及径向尺寸为无限大的介质模型。图1显示了套管井内的超声波传递模型。本文假设井眼为无限长的规则圆柱状，井内为理想流体，井外介质可以看作完全弹性体，在井轴上某一位置放置一个单源超声波探头，距离该探头一定距离处设置一个接收器接收回波，将受到的回波进行处理和分析可以得到井下的情况。

本文取套管井的套管内径为4.7 cm，井液密度为1.2 kg/m3，井液中纵波声速为1 680 m/s[7]。为了讨论换能器在不同的频率工作时对套管井内超声场分布的影响，分别建立3个几何模型，分别计算换能器在20，30，40 kHz情况下工作时的超声场。

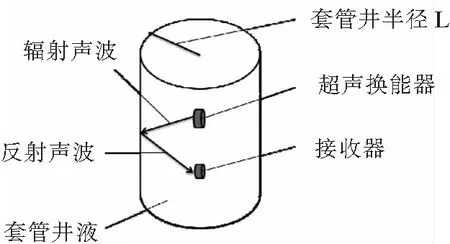
图1 套管井内超声波传递的物理模型

2 仿真模型建立与网格划分

2.1 建立模型

运用comsol创建几何模型，该模型为轴对称模型，为了简化计算，本研究取模型的一半进行计算。在几何模块中长度单位设置为“mm”，角度单位设置为“度”。首先创建一个高度为500 mm，半径为L=47 mm的半圆柱体，在距离模型上端的套管井横截面50 mm处，创建一个半径为5 mm的圆面。图2显示了套管井的几何模型。

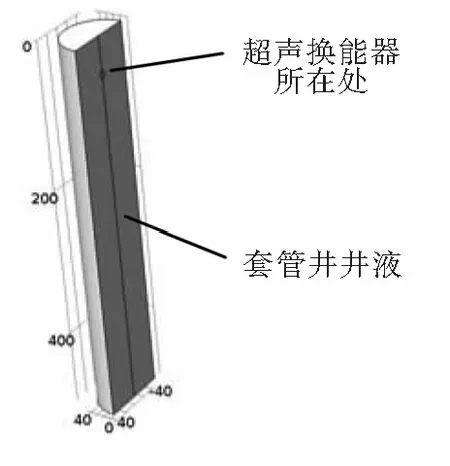
图2 套管井的几何模型

2.2 网格划分

在“组件”模块下进行网格划分，为了避免严重的失真，我们取网格最大单元格尺寸为“波长/频率/5”，最小单元格尺寸为0.01 mm。因为该模型结构简单，不存在复杂的交界面，因此直接使用自由剖分四面体网格功能。图3显示了网格剖分效果。

3 数值模拟计算及结果分析

3.1 数值模拟计算

本研究针对每个模型，分别计算超声频率f为20，30，40 kHz的情况下，套管井内的超声场分布。

图3 网格剖分结果

本文选取换能器端面振幅为a=10 μm，井液密度为ρ=1.2 kg/m3，井液纵波声速为c=1 680 m/s。根据公式P=ρcωa，ω=2πf可以计算得到3种频率下换能器端面的声压值P1、P2、P3。

根据公式Z=ρc可以计算得到套管井外壁面的声阻抗[8]。

本文选用“压力声学—频域”模块进行计算，该模型所需参数如下：密度1 200 kg/m3；声速1 680 m/s；P1为2 532.096 Pa；P2为3 798.144 Pa；P3为5 064.192 Pa；阻抗2 016 000 Pa·s/m；温度293.15 K。

换能器端面设置为inlet1，组件耦合设置为积分intop1，积分源设置为边界，选取inlet1。局部变量输入变量为“ ”。换能器模型边界条件设置为球面波辐射，套管井外壁面设置为阻抗，球面波辐射下的入射压力场输入不同频率对应的声压值，研究设定中频率设置为对应频率，设置完成后进行计算。

3.2 结果分析与对比

模拟完成后，在结果功能下调出声压等值面，在等值面功能中表达式处输入 可以得到声压等值面。不同频率下工作的换能器，在套管井中辐射声场如图4。

(a) 20 kHz; (b) 30 kHz; (c) 40 kHz图4 换能器在不同频率下工作时辐射的声场

根据图4我们可以发现，当换能器端面半径为5 mm时，随着频率增大，等值面的整体数值明显增大。这是因为辐射声压相同的换能器，随着工作频率的增加，其辐射的超声波功率也增大。30 kHz工作时声压最大值比20 kHz工作时增加352.70%，40 kHz工作时比30 kHz工作时最大声压值高25.07%。这是因为在30 kHz工作时，套管井壁面的阻抗引起的声衰减增幅较小，当频率增大到40 kHz时，套管井壁面的声阻抗引起的衰减量的增幅较大。实际工程应用中，我们希望远场声场整体较强，提高回波检测的信号的可靠性，同时希望衰减较小，减少误差。

工程上采样数据以声压级为单位，因此本文进一步分析套管井轴线上的声压级分布。在数据集中建立一个三维截线，起始点为超声换能器中心，并使该截线与井轴重合。在结果模块中建立一维绘图组，选取线图，在该模块表达式中输入acpr.pt，导出从换能器中心沿井轴方向的声压级分布图，如图5所示。

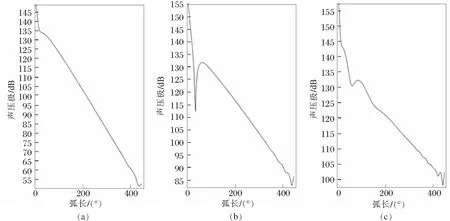
(a) 20 kHz; (b) 30 kHz; (c) 40 kHz图5 从换能器中心沿井轴方向的声压级分布

由图5可以看出，当频率为20 kHz时，井轴上声压级分布较为平滑；当频率为30 kHz时，在近场区域声压级会发生突变，2倍波长至5倍波长距离内的声压级分布较为平滑；当频率为40 kHz时，近场区域声压级不稳定，3倍波长距离至5倍波长距离内的声压级分布较为平滑。随着频率的增大，远场声压级越来越大，近场区域不规律性也越来越大。

实际工程应用中，很少在近场区域设置超声接收器。但是近场区域稳定性越差，越不利于超声换能器本身工作的稳定性。根据在该模型的计算结果，20 kHz时套管井内声压太小，容易受到外界环境噪声的干扰，40 kHz时衰减太大，会在测井过程中引起较大的误差，因此选取最佳的工作频率为30 kHz，采样处设置在距离换能器中心4倍波长处。

4 结 语

本文应用COMSOL对套管井内的超声场分布进行了数值计算，得到了套管井内换能器在不同频率下工作时辐射的超声场。对比不同频率下的超声场对设计超声测井设备以及修正超声成像有积极意义，进行三维空间内的超声场声压分布可以预测套管井壁面阻抗引起的衰减，对比井轴上的声压级分布可以得到较好的工作频率和采样位置。本论文可以为更精确的超声测井技术提供参考依据。