三参数幂函数在水位—流量关系曲线中的应用
王新刚
(辽宁省锦州水文局,辽宁锦州121000)
三参数幂函数在水位—流量关系曲线中的应用
王新刚
(辽宁省锦州水文局,辽宁锦州121000)
利用规划求解的方法,通过三参数幂函数来拟合水位~流量关系曲线,虽然拟合精度较高,但在低水处误差较大,定线精度不够好,有的甚至不能通过关系曲线检验。作者通过分段拟合关系曲线,并将涉及参数通过归纳解析的方法,将参数从常数转变成与水位相对应的系列参数,最后利用三参数幂函数公式求得流量,建立单一水位~流量关系曲线,提高了拟合精度。
拟合;定线精度;水位~流量关系曲线
1 概况
水文工作者一直以来利用三参数幂函数来拟合水位—流量关系曲线,试图利用计算公式对给定的水位计算其相应的流量。三参数幂函数的公式(1):

其中:a,b为求解参数;c通常认为是河底高程,m;y为水位,m;x为流量,m3/s。
根据实测水位、流量资料,利用规划求解方法,可以得出最优解,从而确定参数a,b,最后按照公式y=axb+c,获得水位~流量关系曲线的函数公式,并求得相应水位的流量。
利用三参数幂函数公式虽然拟合精度较好,但在低水处误差较大,并且在定线精度上,仍不符合《水文资料整编规范》关于定线精度的要求,在关系曲线检验时也存在一定的问题。下面是锦州水文局缸窑口水文站(二类精度水文站)2011— 2014实测数据,利用规划求解方法,拟合的水位~流量关系线,并进行定线精度检验。发现除L3标准差与随机不确定度接近精度指标以外,其他关系线均与定线精度指标相差较大。

表1 缸窑口水文站历年水位-流量关系线拟合成果表
2 解决方法
2.1 分段拟合
以缸窑口水文站水位—流量关系线样本数最多的L2为例,按照水位从低到高排列,每组包含5个样本,每次计算向高水位滑动3个样本,以此类推。分别求解参数,并计算其标准差与随机不确定度。根据每组滑动数据,确定拟合精度最高的水位作为参数的特征水位。下面就两组数据作为实例,详见表2,3。
2.2 建立水位与参数a,b之间关系
将八组数据归纳后,可以看出,发现参数a取值与水位成反比,参数b取值与水位成正比。水位40.18,40.66在其参与的两组计算中拟合精度都是最高,按照水位与参数a,b的关系舍去不符值。分段拟合后,数据定线精度较高,均符合《水文资料整编规范》关于定线精度的要求。详见表4。
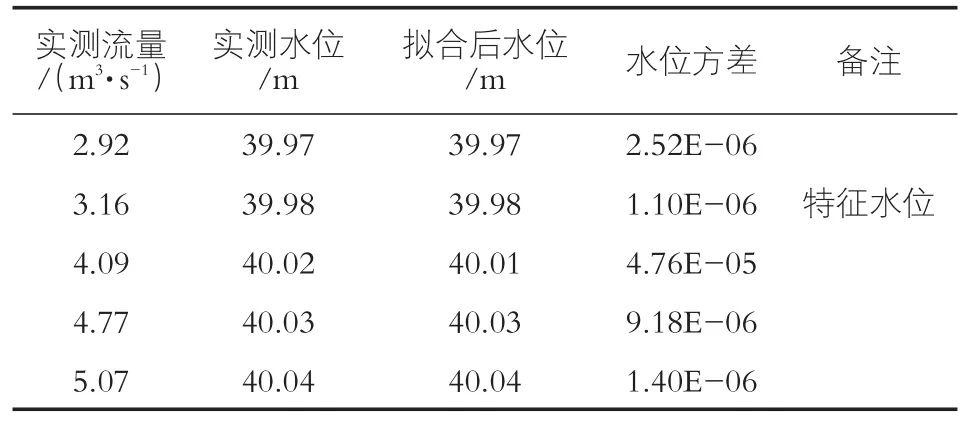
表2 L2关系线第1组数据一览表

表3 L2关系线第2组数据一览表
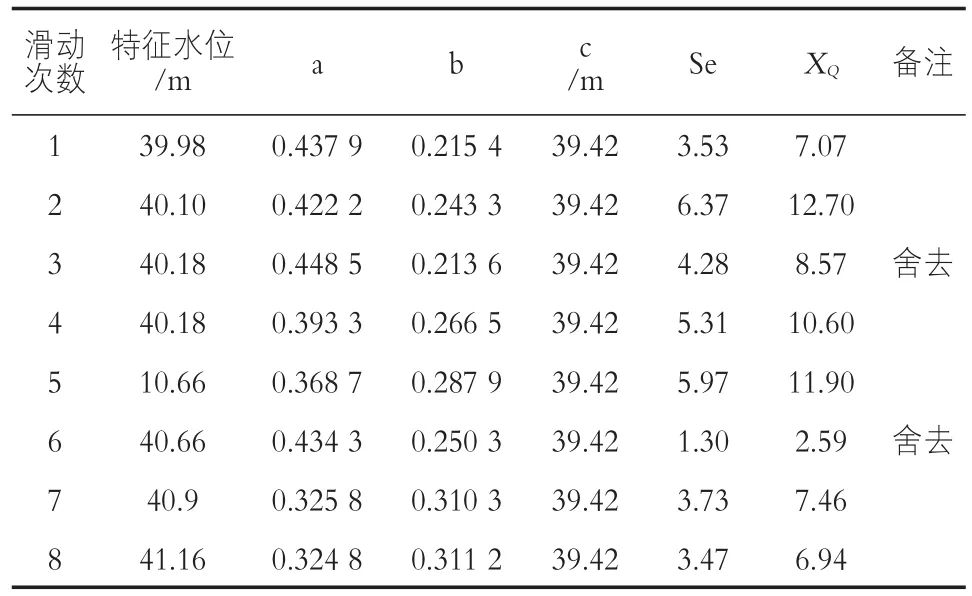
表4 L2关系线分段拟合成果
建立水位 y与参数a,b的关系,如图1所示。利用excel导出公式可以看出y与a,b之间关系符合y=a′x2+b′x+c′函数。运用规划求解,解出函数最优解为式(2)(3)。
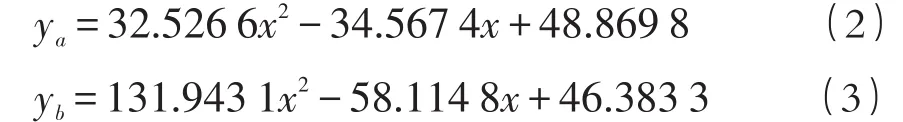
其中:y为水位,m;x为式1-1中的参数a或b。
2.3 复核拟合结果
根据L2实测系列水位通过公式(2)(3)计算对应的参数a,b值,形成系列值。然后利用式(1)计算相应流量。详见表5。
依据《水文资料整编规范》中定线精度的规

图1 水位与参数关系图
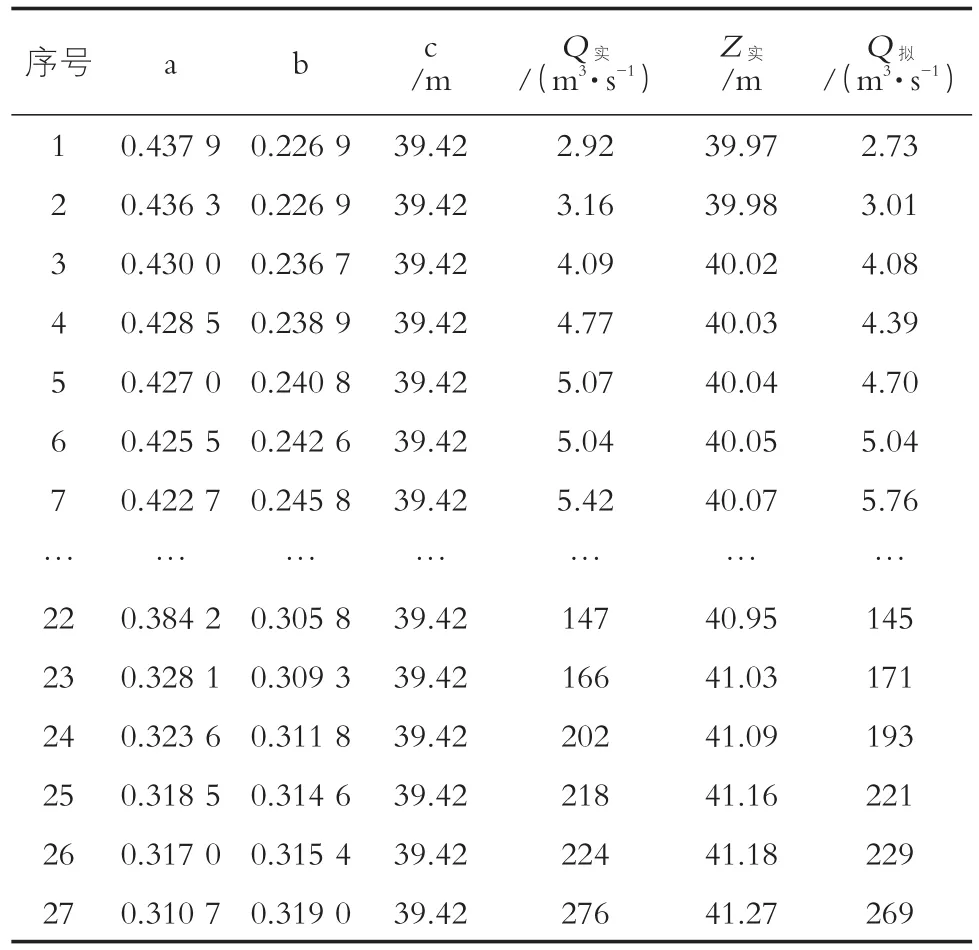
表5 缸窑口L2水位~流量关系线最终拟合成果表
注:Q实为实测流量,Z实为实测水位,Q拟为计算流量值定,标准差的公式为:

其中:Se——实测点标准差;Qi——第i次实测流量,m3/s;Qci——第i次实测流量Qi相应的曲线上的流量,m3/s;n——测点总数。
求得Se等于5.41,XQ为10.82。符合二类精度站XQ<12的要求,定线合理。
3 结论与存在问题
3.1 结 论
利用上述方法将其余4条关系曲线做公式拟合时,虽L1与L4线仍未达到精度标准。但关系线精度都有不同程度的提高,大多数关系拟合较好。利用公式拟合水位流量关系曲线,能够方便查出流量值,并对人工画线具有指导意义。能够得出结论:
1)样本数越多且水位变幅较小的关系线拟合精度较高;
2)进行水位滑动后,精度均有大幅提升。
3.2 存在问题
利用公式拟合可以较好的将水位流量关系曲线进行简化,更方便快捷的得出水位流量关系。但在建立水位与参数a,b关系时,确定其相应参数较为关键,当关系线实测水位变幅较大时,容易产生突出点,误差点较大主要发生在峰值时,导致精度偏差过大。应合理分析参数a,b或进行分段拟合。
利用分段拟合水位与参数a,b,选取拟合精度最高的作为代表值,但在有些关系曲线上,仍不能很好的代表水位与参数a,b之间关系。如何取得更具代表性的水位与参数a,b之间的关系,仍是下一步应该研究重点。
[1]张云辉.三参数幂函数在水位~流量关系曲线拟合中的应用[J].东北水利水电,2012(06):43-44.
[2]刘云程.用对数函数选配水位流量关系曲线[J].水文,1984(06):39-41.
[3]程雪源,范永波.河流水位-流量关系的Excel拟合方法研究[J].吉林水利,2013(08):24-25+28.
[4]SL 247-1999,水文资料整编规范[S].
TV 122 < class="emphasis_bold"> [文献标识码]B
B
1002—0624(2017)09—0031—02
2016-08-17

