基于手征超材料的90◦TH z极化偏转器

续凯凯,肖中银,刘德君,唐敬瑶,马孝龙,王子华

(上海大学通信与信息工程学院,上海200444)

基于手征超材料的90◦TH z极化偏转器

续凯凯,肖中银,刘德君,唐敬瑶,马孝龙,王子华

(上海大学通信与信息工程学院,上海200444)

提出了一种新的手征结构,该结构由介质板及其上下表面的双L谐振器组成.仿真结果表明,该结构在THz波段可实现对x-极化波的宽频段、多频段的90◦极化偏转.特别是在2.56 THz处,这种新的结构能够实现对线极化波(x-极化波和y-极化波)的90◦极化偏转,而此时的椭圆度约为0◦.基于线极化波的电场分布,详细分析了极化偏转的物理机制.理论上,该手征结构也可以用来设计微波波段或近红外波段的90◦极化偏转器.

手征超材料;极化偏转;线极化波;太赫兹波

近年来,手征超材料因其独特的电磁特性引起了许多科研工作者的关注[1].自2004年Pendry[2]利用具有手征性的超材料结构首次实现负折射以后,手征超材料的研究已成为电磁领域研究的新热点.之后,在微波波段、THz波段,甚至在光频段,许多结构复杂的手征超材料被相继提出[3-7].2006年,Fedotov等[8]在平面手征超材料中首次发现了非对称传输特性.这一新的特性再次引发了人们对手征超材料的研究热情,并迅速获得了许多有意义的成果,不仅实现了线极化波[9]、圆极化波[8]的非对称传输,而且还可以由一种结构同时实现对线极化波和圆极化波的非对称传输[10-11].除了负折射、非对称传输特性[12-14]以外,手征超材料也拥有其他奇异特性,例如,巨大的光活性[15-18]、圆二色性、极化偏转特性等.目前,在微波波段对线极化波实现90◦极化偏转的手征结构已经被提出,但在THz波段可实现90◦极化偏转的手征结构却不多,且已有的手征结构仅能实现对x-极化波或y-极化波的90◦极化偏转,可以同时实现对x-极化波和y-极化波90◦极化偏转的手征结构还鲜有报道.因此,研究THz波段手征超材料的极化偏转特性具有非常重要的意义.

本工作提出了一种平面手征结构,实现了对线极化波的90◦极化偏转.本工作分析了所提出手征结构实现极化偏转时的旋光角及椭圆度,发现在2.56 THz时,椭圆度幅值大小约为0◦,实现了对线极化波(无论是x-极化波还是y-极化波)的90◦极化偏转.

1 理论分析

假设一束线极化波沿+z方向垂直入射到具有双L谐振器的手征结构中,入射波电场可表示为Ei(r,t)=(Ix,Iy)Tei(kz-ωt),其中ω为角频率,k为波矢,Ix和Iy分别为入射波沿x-极化方向和沿y-极化方向的复振幅.通过手征结构后的透射波电场可表示为Et(r,t)=(Tx,Ty)Tei(kz-ωt),其中Tx和Ty分别为透射波沿x-极化方向和沿y-极化方向的复振幅.入射波电场与透射波电场之间的关系可由T矩阵[19]来表示:

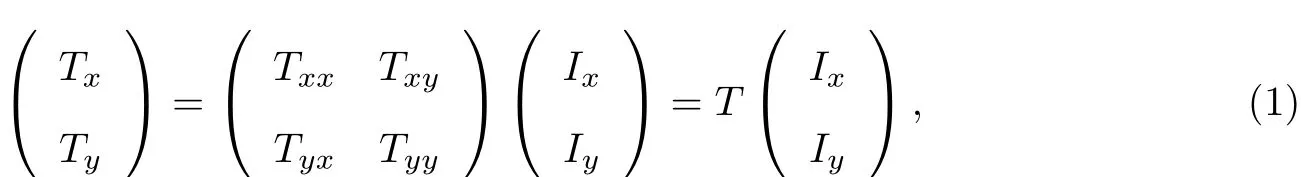
式中,Tij中的下标i,j分别表示沿x-极化方向或y-极化方向的透射波和入射波,其中矩阵主对角线元素Txx和Tyy为共极化传输系数,逆对角线元素Txy和Tyx为交叉极化传输系数.

对于手征结构可实现的极化偏转角θ及椭圆度η可通过以下两个公式[20]进行计算:

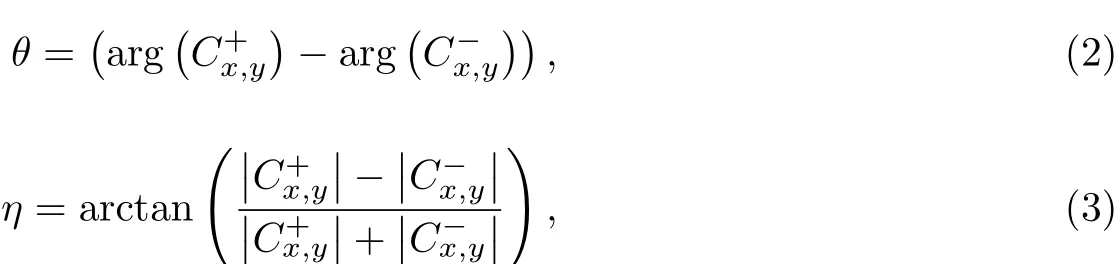
式中,

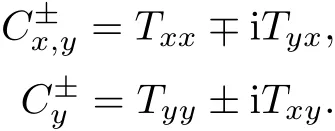
2 仿真实现及分析

图1为手征超材料的微单元结构,该结构的介质板采用相对介电常数εr=2.7的硅材料(理想介质),厚度d=10µm.结构仿真采用基于时域有限差分法的商业软件——CST微波工作室(Computer Simulation Technology Microwave Studio)来完成.在仿真实验中,在x和y方向设置周期边界条件,在z方向设置吸收边界条件.

手征单元结构的参数详述如下:ax=ay=80µm,L=64µm,w=10µm,g=22µm.金属银的厚度t=5µm,其金属结构在THz波段的色散损耗关系利用Drude模型[21]模拟:

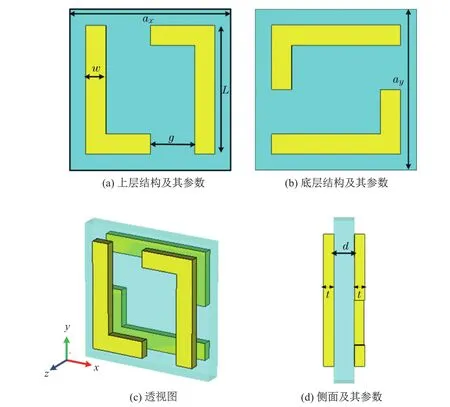
图1 手征材料的结构单元Fig.1 Geometry of unit cells of the designed chiral structure

式中,ωp=2π×2.175×1015rad/s,ωc=2π×4.35×1012rad/s.

根据上述结构,本工作仿真了线极化波入射到平面手征材料后的传输特性,结果如图2所示,其中图2(a),(b)分别表示线极化波沿+z和–z方向传输时的曲线.可以看出,在全频段内共极化传输系数几乎完全相等(Txx=Tyy),除了f=1.14以及2.84 THz两频点外,交叉极化在各频点的幅值均有较大的差别(Tyx/=Txy).

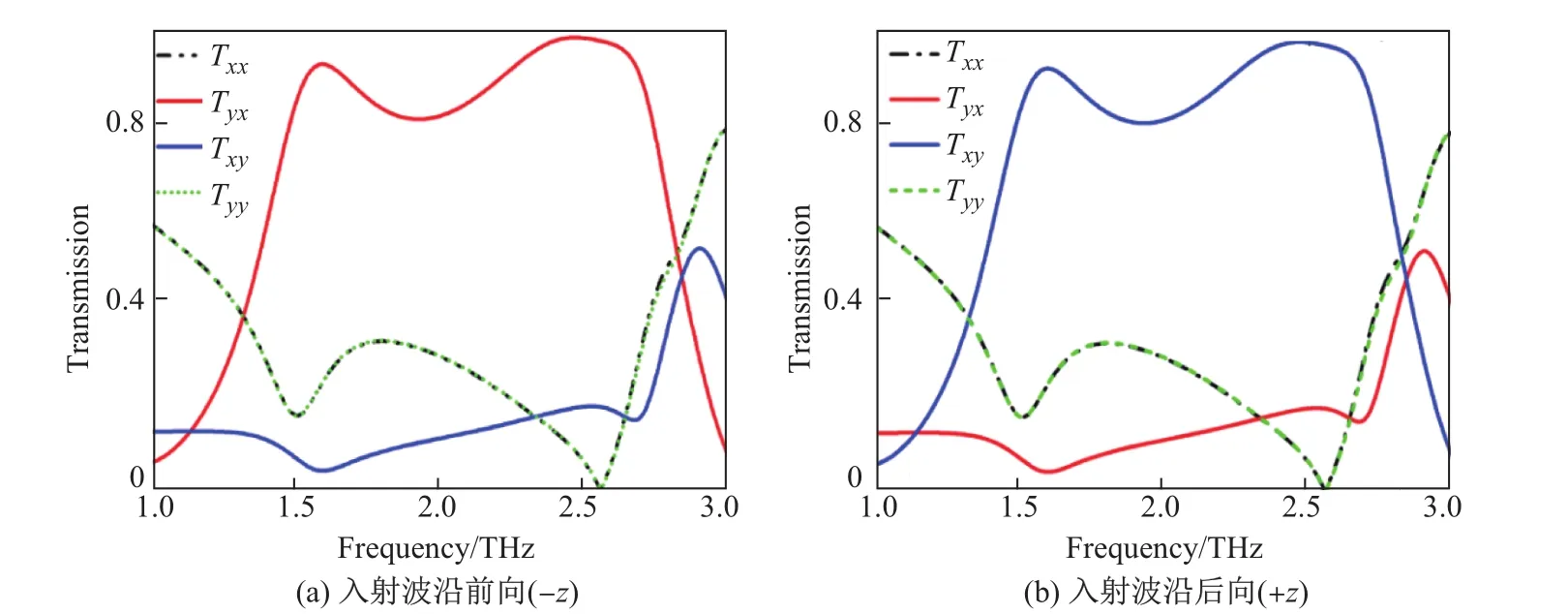
图2 入射波沿前向(-z)和后向(+z)的传输系数的幅值F ig.2 Magnitudes of the transmission coeffi cients of forward(-z)and backward(+z)

根据图2中的传输系数随频率的变化关系,本工作利用式(2)和(3)计算得到手征结构的极化偏转角和椭圆度随频率变化的曲线,结果如图3所示.可以看出:x-极化波在较宽的频段(1.67～2.71 THz)内实现了良好的极化偏转效果,在1.67～2.36 THz频段内实现了约-90◦的极化偏转,而在2.36～2.71 THz频段内实现了约+90◦的极化偏转.因此,本工作提出的手征结构实现了对x-极化波宽频段、双频段近90◦的极化偏转,而y-极化波在该频段内的极化偏转角度逐渐增大,在2.56 THz处可达到约90◦的极化偏转.

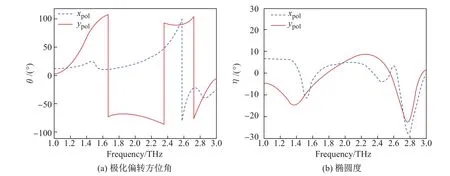
图3 极化偏转方位角和椭圆度Fig.3 Polarization rotation azimuth angles and ellipticity

从图3中还可以看出,在1.56～2.56 THz频段范围内,椭圆度的幅值也较小.为了直观地比较手征结构的极化偏转方位角和椭圆度的对应关系,本工作选择了3个频点:1.59,2.47, 2.56 THz,记录各频点对应的椭圆度及极化偏转方位角,结果如表1所示.可以看出,在3个频点,手征结构均能实现对x-极化波约90◦的极化偏转,而此时各频点对应的椭圆度分别为-6.69◦,4.84◦,-0.43◦.由此可见,本工作提出的手征结构对x-极化波可实现多频点处的90◦极化偏转,而此时的椭圆度均小于10◦.对y-极化波来说,在3个频点处的椭圆度幅值也不大,在1.59和2.47 THz处的极化偏转方位角分别为9.14◦,65.01◦,不能实现90◦极化偏转;但在2.56 THz处,手征结构实现了椭圆度为-0.05◦(约为0◦),极化偏转角约为90◦的极化偏转.综合上述分析,在2.56 THz处,本工作提出的手征结构很好地实现了对线极化波(x-极化波和y-极化波)的90◦极化偏转.

表1 3个频点处椭圆度及极化偏转方位角Tab le 1 Ellipticity and polarization rotation azimuth angles of the three frequency points

为了验证本计算结果的正确性,同时更好地理解所提出手征结构实现极化偏转的物理机制,本工作详细分析了线极化波入射时的入射波及透射波的电场分布.通过对1.59,2.47及2.56 THz处入射电场及透射电场方向的分析,进一步说明所提出手征结构实现90◦极化偏转的作用机理,结果如图4所示.

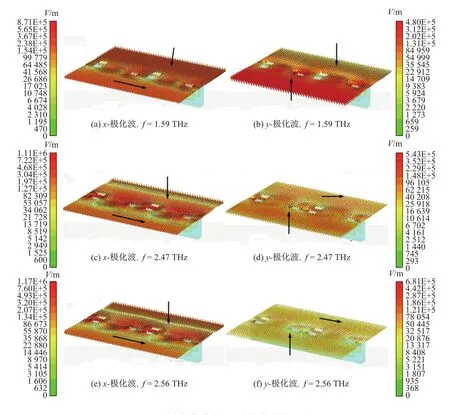
图4 线极化波在不同频率的电场分布Fig.4 Electric field distributions of linearly polarized wave at diff erent frequencies

从图4中可以直观地看出,对x-极化波,在2.47及2.56 THz(见图4(a)和(e))处均能实现对电场的约90◦极化偏转(入射电场沿+x方向,透射电场沿-y方向);而在1.59 THz(见图4(c))处,可实现的极化偏转角大于90◦(计算值为102.20◦).对y-极化波,在1.59 THz处,电场方向发生了反向偏转;在2.47 THz处,电场方向由+y向+x方向偏转,但由图4(d)容易看出,此时的偏转方位角小于90◦(计算值为65.01◦);而在2.56 THz处,电场方向由+y偏转为+x方向,实现了对y-极化波的90◦极化偏转.以上结果表明,理论计算结果与仿真结果十分相近.在f=2.56 THz处,所提出手征结构实现了对线极化波(x-极化波和y-极化波)的90◦极化偏转.

3 结束语

本工作提出了一种由介质板及其上下表面的双L谐振器构成的新型手征结构,在THz波段实现了对线极化波的90◦极化偏转.通过分析极化偏转方位角及椭圆度随频率变化的曲线,得出在2.56 THz处,所提出手征结构可实现对x-极化波和y-极化波90◦的极化偏转,而此时该频点所对应的椭圆度均约为0◦.为了便于理解极化偏转的物理机制,分析了不同频点(1.59, 2.47,2.56 THz)处的电场分布,证明了本实验结论.理论上,利用所提出的征结构同样可以在其他频段(如微波波段、近红外波段)实现对线极化波的90◦极化偏转.

[1]徐晓雪,肖中银,马全文,等.手征负折射媒质对称平板波导的色散特性[J].上海大学学报(自然科学版),2015,21(2):206-212.

[2]PENDRY J B.Achiral route to negative refraction[J].Science,2004,306:1353-1355.

[3]ZHANG S,PARK Y S,LI J,et al.Negative refractive index in chiralmetamaterials[J].Phys Rev Lett,2009,102(2):023901.

[4]DONG J,ZHOU J,KOSCHNY T,et al.Bi-layer cross chiral structure with strong optical activity and negative refractive index[J].Opt Express,2009,17(16):14172-14179.

[5]ZHOU J,DONG J,WANG B,et al.Negative refractive index due to chirality[J].Phys Rev B, 2009,79(12):121104.

[6]PLUME,ZHOU J,DONG J,et al.Metamaterial with negative index due to chirality[J].Phys Rev B,2009,79(3):035407.

[7]LI Z,ZHAO R,KOSCHNY T,et al.Chiralmetamaterials with negative refractive index based on four“U”split ring resonators[J].Appl Phys Lett,2010,97(8):081901.

[8]FEDOTOV V A,MLADYONOV P L,PROSVIMIN S L,et al.Asymmetric propagation of electromagnetic waves through a planar chiral structure[J].Phys Rev Lett,2006,97:167401.

[9]LIU D J,X IAO Z Y,MAX L,et al.Dual-band asymmetric transmission of chiralmetamaterial based on complementary U-shaped structure[J].Appl Phys A,2015,10:1007.

[10]MENZLE C,HELGERT C,ROCKSTUHL C,et al.Asymmetric transmission of linearly polarized light at opticalmetamaterials[J].Phys Rev Lett,2010,104(25):253902.

[11]LIUD J,X IAO Z Y,MAX L,et al.Asymmetric transmission of linearly and circu larly polarized waves in metamaterial due to symmetry-breaking[J].Applied Physics Express，2015,8:052001.

[12]PLUN E,FEDOTOV V A,ZHELUDEV N I.Planarmetamaterialwith transmission and refl ection that depend on the direction of incidence[J].Appl Phys Lett,2009,94(13):131901.

[13]SINGHR,PLUME,MENZELC,et al.Terahertzmetamaterialwith asymmetric transmission[J]. Phys Rev B,2009,80(15):153104.

[14]FEDOTOV V A,SCHWANECKE AS,ZHELUDEV N I,et al.Asymmetric transmission of light and enantiomerically sensitive plasmon resonance in planar chiralnanostructures[J].Nano Lett, 2007,7(7):1996-1999.

[15]YE Y,HE S.90◦polarization rotator using a bilayered chiralmetamaterial with giant optical activity[J].Appl Phys Lett,2010,96(20):203501.

[16]X IONG X,SUNW H,BAO Y J,et al.Construction of a chiralmetamaterial with a U-shaped resonator assemb ly[J].Phys Rev B,2010,81(7):075119.

[17]KWOND H,W ERNER P L,W EMERD H.Optical planar chiralmetamaterial designs for strong circular dichroismand polarization rotation[J].Opt Express,2008,16(16):11802-11807.

[18]PLUME,FEDOTOV V A,SCHWANECKE AS,et al.Giant optical gyrotropy due to electromagnetic coupling[J].Appl Phys Lett,2007,90(22):223113.

[19]MENZEL C,ROCKSTUHL C,LEDERER F.Advanced Jones calculus for the classification of periodic metamaterials[J].Phys Rev A,2010,82:053811.

[20]MUTLU M,AKOSMAN AE,SEREBRYANNIKOV AE,et al.Asymmetric chiral metamaterial circular polarizer based on four U-shaped split ring resonators[J].Opt Lett,2011,36(9):1653-1655.

[21]LINDEN S,ENKRICH C,W EGENER M,et al.Magnetic response of metamaterials at 100 terahertz[J].Science,2004,306:1351-1353.

90◦TH z polarization rotator based on chiral metamaterials

XU Kaikai,XIAO Zhongyin,LIU Dejun,TANG Jingyao, MAXiaolong,WANG Zihua
(School of Communication and Information Engineering,Shanghai University,Shanghai200444,China)

This paper proposes a novel chiral structure consisting of double L resonators fabricated on both sides of the dielectric substrate.Simu lation results reveal that the structure can achieve broadband and multi-band 90◦polarization rotation of x-polarization wave in a THz band.In particular,the chiral structure can realize 90◦polarization rotation for x-polarized and y-polarized waves at 2.56 THz.Meanwhile,ellipticity of the linear polarization wave isabout 0◦.The physicalmechanismof linearly polarized wave conversion based on electric fields isanalyzed.The structure can also beused to design 90◦polarization polarizer in other bands,for instance,microwave and near in frared regions.

chiralmetamaterial;polarization rotation;liner polarization wave;THz wave

O 441.4

A

1007-2861(2017)04-0517-07

DO I:10.12066/j.issn.1007-2861.1679

2015-09-01

国家自然科学基金资助项目(61275070);上海市自然科学基金资助项目(15ZR 1415900)

肖中银(1964—),男,教授,博士生导师,研究方向为手征特异材料、光波导表面模特性等.

E-mail:zhyxiao@staff.shu.edu.cn