引信MEMS微结构可靠性仿真及实现方法

涂宏茂，孙志礼，姬广振，刘 勤

(1．东北大学机械工程与自动化学院，辽宁 沈阳 110819；2．中国兵器科学研究院，北京 100089)

引信MEMS微结构可靠性仿真及实现方法

涂宏茂1,2，孙志礼1，姬广振2，刘 勤1,2

(1．东北大学机械工程与自动化学院，辽宁沈阳110819；2．中国兵器科学研究院，北京100089)

针对目前引信MEMS微结构设计中缺乏高效的可靠性量化仿真方法的问题，提出了基于结构性能仿真的可靠性仿真分析及其实现方法。该方法以ANSYS软件为例给出CAE程序的集成方法和实现步骤，解决可靠性分析程序对有限元软件工具的自动调用问题；采用试验设计和近似建模相结合的方法，有效降低可靠性分析程序对有限元仿真的调用次数，在此基础上，给出结构可靠度计算和灵敏度分析的基本原理；提出可靠性仿真实现的总体程序框架，给出各主要模块的功能及其主要函数的伪代码。实际验证结果表明，该仿真方法具有可行性和实用性。

引信可靠性；MEMS微结构；可靠性仿真；有限元方法；可靠度

0 引言

目前，有限元等数值仿真方法越来越多地应用到引信MEMS的设计分析中。尤其是对于MEMS微结构(如引信用的MEMS悬臂梁、弹簧等，结构特征尺寸在1 μm至1 mm范围内)而言，它们常具有相对的运动或相互的表面作用，利用有限元等仿真方法可以在设计阶段很好地揭示其运动规律和力学特性[1-5]，并发现潜在的失效模式和失效原因，为设计改进与优化提供了有益的参考。如果能在此基础上，进一步开展量化的可靠性分析，一方面给出结构设计方案的可靠性水平，另一方面明确影响结构可靠性的主要因素，对于实现设计阶段的可靠性预测和改进，具有重要的工程意义。从国外的一些研究文献[6-8]来看，解决这一工程需求的基本思路是：将结构可靠性理论与有限元仿真方法相结合，进行MEMS微结构的可靠性仿真分析与优化设计。但在实践过程中，仍然存在两个方面的问题：一是如何在可靠性分析程序中方便地集成CAE仿真程序或工具(如ANSYS、COMSOL Multiphysics等，后续简称为CAE程序)，从而提高计算效率；二是如何减少可靠性分析程序对有限元软件的调用次数，从而降低计算成本。本文结合上述的基本思路，并针对如何在可靠性分析中高效集成CAE程序且有效减少调用次数问题，给出引信MEMS微结构可靠性仿真和实现方法。

1 主要问题及其解决思路

根据结构可靠度理论[9]，引信MEMS微结构失效概率模型可以写为：

Pf=P(g(x)<0)

(1)

式(1)中，P(*)表示事件*发生的概率；g(x)是表征微结构状态的函数，常称为功能函数，g(x)<0表示微结构失效，g(x)>0表示微结构安全，g(x)=0表示极限状态；x(x1,…,xn)T为随机变量向量。对应的可靠度模型为：

R=1-Pf=P(g(x)≥0)

(2)

在实际应用中，功能函数g(x)可以进一步改写为

g(x)=s(x)-y(x)

(3)

式中，s(x)为广义强度，可以是微结构材料强度、允许最大变形量、允许最大应力值等；y(x)为广义应力，可以是微结构应力响应、应变响应等；二者都可以是随机变量向量x的函数。

将式(3)代入式(1)可以得到

Pf=P(s(x)-y(x)<0)

(4)

本文主要讨论基于有限元仿真获得广义应力y(x)的情况。针对式(4)所示的失效概率模型的求解，需要解决两个方面问题：一是如何在计算中集成CAE程序，方便地将可靠性分析的过程数据(如变量样本值)传递给CAE程序作为输入数据，又可以及时获得CAE程序的求解结果，作为可靠性分析下一步骤的输入数据；二是如何用尽可能少的CAE程序调用次数，完成预定的可靠性分析功能。

针对第一个问题，本文将以ANSYS软件为例说明CAE集成方法，包括命令流文件更新、软件调用、求解结果获取等。针对第二个问题，本文将构建y(x)的近似模型，再利用蒙特卡洛法模拟法或迭代方法(如一次二阶矩法及其改进方法等)进行可靠性求解。其中，近似建模所需要的样本数据由试验设计方法获得。

2 可靠性仿真方法

2.1 仿真流程

结合上述问题及其相应的解决思路，可以得到基于有限元仿真的引信MEMS微结构可靠性仿真流程，如图1所示。

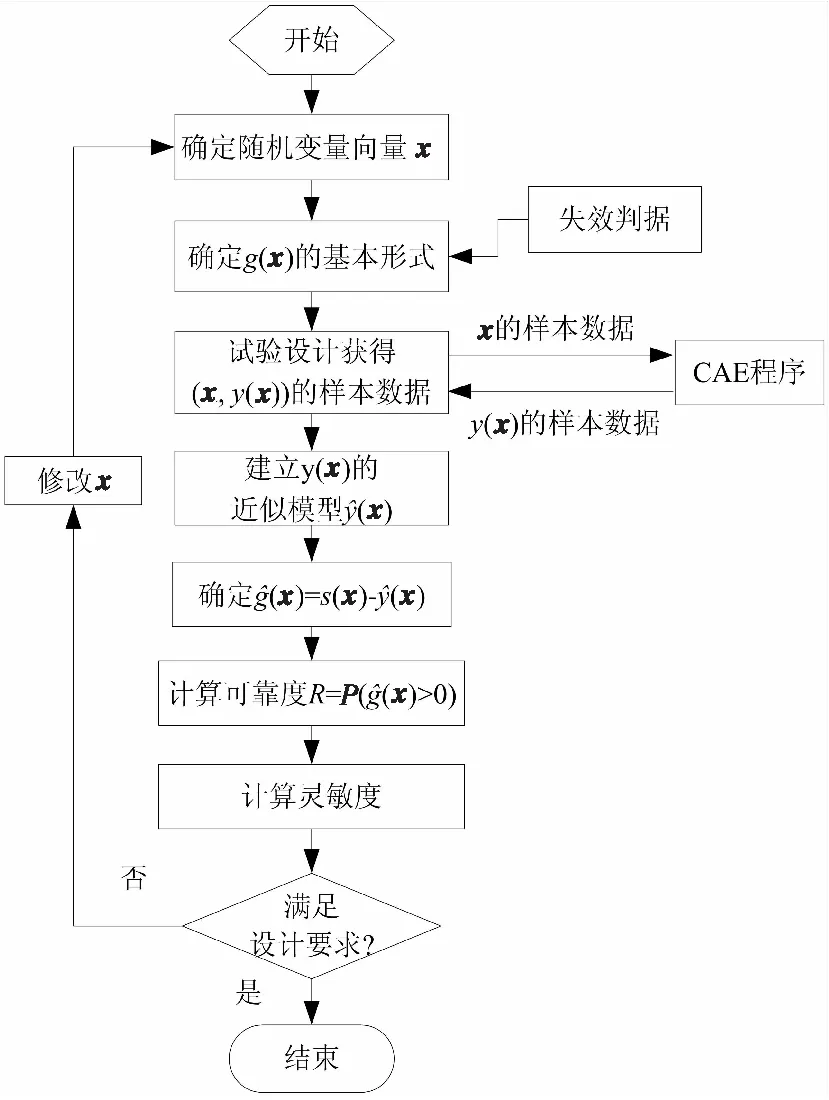
图1 引信MEMS微结构可靠性仿真流程Fig.1 Reliability simulation procedure for micro-structure in fuze

图1中，需要结合引信MEMS微结构失效判据，以及应力-强度干涉的基本理论，得到功能函数g(x)的基本表达形式。常见的功能函数的基本形式如表1所示。

表1 常见的功能函数的基本形式

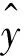
2.2CAE集成方法

在试验设计中，采用全因子设计或部分因子设计等方法[10-11]获得x的样本数据，针对每一组样本数据，调用一次CAE程序进行求解，获得y(x)的一组输出数据。对所有的x样本数据进行同样的操作，可以得到(x,y(x))的样本数据。以ANSYS为例，给出各组样本计算的流程，如图2所示。

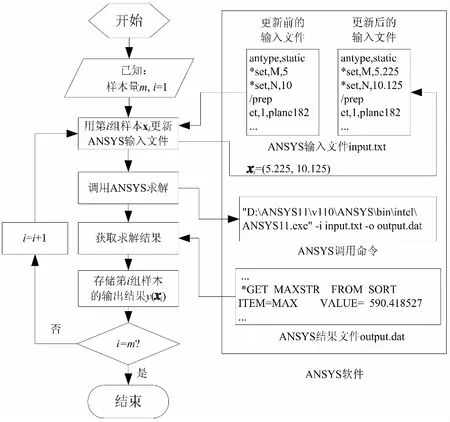
图2 集成ANSYS的样本计算流程Fig.2 Samples calculation procedure based on ANSYS

可以看出，在每一次的ANSYS调用过程中，需要完成三个核心的步骤：

1)依据i组样本数据xi修改ANSYS输入文件中的变量值，即将命令流中的“*set,M,5”与“*set,N,10”分别修改为“*set,M,5.225”和“*set,N,10.125”。在具体实现时，可以通过搜索关键字符串(如“*set,M”或“*set,N”)的方式，获取待处理的数据文本在命令流文件中的位置，然后用新的样本数据替换之，形成新的命令流文件。

2)以批处理方式(Batch Mode)调用ANSYS进行求解，这是采用后台调用的方式，避免ANSYS软件界面的反复闪现问题。在具体实现时，若采用Windows系统，那么可以将调用命令写入后缀名为bat的文件，然后执行该文件，即可实现ANSYS的后台调用。

3)获取本次ANSYS计算结果，如最大应力值或应变值等。在具体实现时，与命令流文件更新方法类似，可以通过搜索关键字符串(如“ITEM=MAX VALUE”)，获取待提取数据文本所谓的位置，然后依据该位置信息获取相应的结果数据。

其他的CAE软件，如ADAMS、HyperWorks等，尽管各自的输入、输出文件格式，以及后台调用命令的都不尽相同，但是都可以采用这一方式进行集成。

2.3 近似建模

为了便于后续的可靠性分析，在获得(x,y(x))样本数据的基础上，需要构造y(x)的近似模型。常用的近似建模方法有曲线(面)拟合法和插值法，其中拟合法包括最小二乘法、正交多项式法等，插值法包括Kriging法[11-13]、径向基函数插值等。考虑到后续算例将采用Kriging法建立近似模型，下面简要介绍该方法的基本原理，其他方法可以参考有关的文献。

假设系统的响应值与自变量之间的真实关系可以表示成如下的形式：

y(x)=fT(x)b+z(x)

(5)

式中，fT(x)=[f1(x),f2(x),…,fp(x)]T，fi(x)为回归模型的基函数，通常取为多项式函数，b=(b1,…,bp)T，bi为回归系数，i=1,…,p；z(x)为一个平稳的高斯过程，均值为0，协方差为：

cov(z(xi),z(xj))=σ2R(xi,Xj)

(6)

式中，i,j=1,2,…,m，m为试验次数；R(·,·)为相关函数；σ2为随机过程的方差值。

依据文献[12]，可以得到b和σ2的估计值

(7)

式中，F是由样本点得到的p×m矩阵，F=[fT(x1) …fT(xm)]；Y是各样本点对应的输出，即Y=[y(x1),…,y(xm)]T；R=[Rij]m×m为样本点的相关性矩阵，Rij表达式如下：

(8)

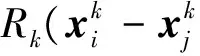
在利用样本数据获得未知参数的估计值后，Kriging的近似模型可以表达为：

(9)

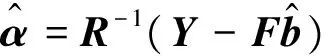
2.4 可靠度与灵敏度分析

结合式(3)和式(9)，可以g(x)得到的近似函数

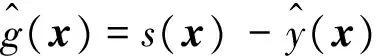
(10)

(11)

式中，β为可靠度指数，满足R=Φ(β)；y为x的等效标准正态随机变量向量，一般通过构造Nataf分布，并进行相应变换得到[14]；L为y的相关系数矩阵经过Choleskey分解得到的下三角矩阵；u是与y相对应的独立标准正态随机变量向量，满足u=L-1y。

参数灵敏度的计算表达如下。

(12)

式中，θ为随机变量x对应的均值或标准差向量；T(x)为u与x的变换函数[13]；σ=[σij]n×n，当i=j时，σij为第i个随机变量的标准差，当i≠j时，σij。

由式(11)和式(12)可以看出，灵敏度计算的核心在于偏导数∂β/∂u的求解。若采用不同的可靠度计算方法时，则该偏导数的计算也有所不同。当采用一次二阶矩等迭代方法时，由于计算过程含有梯度的求解，因此∂β/∂u可以直接获取。当采用蒙特卡洛等抽样方法时，则需要结合可靠度计算公式作进一步推导，得到∂β/∂u的计算结果[15-17]。另外，如果要获得失效概率或可靠度关于随机变量的灵敏度，则可以通过二者与可靠度指数的函数关系，利用复合函数求导获得。

3 可靠性仿真实现

根据上述的方法和流程，可以确定可靠性仿真实现的总体程序框架(如图3所示)，主要包括：仿真工作流、试验设计、近似建模和可靠性分析四个模块，分别命名为Graph、DOE、Model和REL模块。

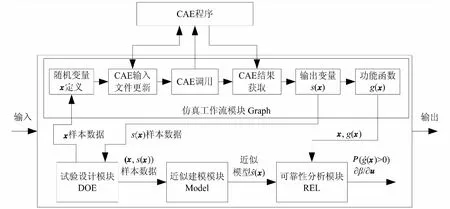
图3 可靠性仿真程序框架Fig.3 Program framework of reliability simulation

下面按模块分析其主要功能及核心函数的框架代码：

1)仿真工作流模块。主要用于定义单次仿真的流程，它包含：输入变量的定义，主要包括随机变量的分布类型、分布参数等；中间过程的定义，包括CAE输入文件、CAE调用命令、CAE求解结果获取等；输出变量的定义，包括广义应力s(x)和功能函数g(x)。该模块核心功能为单次的仿真计算，定义相应的计算函数为Graph.Execute()，框架代码如下：

X = GetSample() '获取随机变量样本值

InputFile = GetCAEInputFile() '获取CAE输入文件

InputFile = RefreshFile(X) '用X数据更新文件

StartCAE(InputFile) '调用CAE进行求解

ResultFile = GetCAEOutputFile() '获取CAE结果文件

S = GetResult(ResultFile) '获取最大应力等结果数据

G = Calculate(S) '计算功能函数值

2)试验设计模块。该模块一方面需要集成各类试验设计的算法用于生成输入变量的样本数据，另一方面需要与仿真工作流模块进行交互，将各组样本数据发送给仿真工作流进行求解，然后获取相应的计算结果，最后得到全部的样本数据。该模块核心功能为输入输出变量样本数据的获取，定义相应的计算函数为DOE.Execute()，框架代码如下：

Xs = CreateSamples() '依据算法生成样本数据

For i=0 to (Xs.Length-1)

'调用工作流进行仿真计算

Y[i]=Graph.Execute(X[i]) '第i组样本数据

End

return (X,Y)

3)近似建模模块。该模块一方面需要集成各类近似建模的算法，另一方面以试验设计模块的样本数据为基础，构建近似模型。该模块核心功能为建模与预测，其中与建模相对应的计算函数定义为Model.Execute()，框架代码如下：

(Xs,Ys)= DOE.Execute () '获取DOE的样本数据

model = SelectModel() '选择模型的类型

beta = GetBeta(model, Xs, Ys) '依据样本计算待定系数

与模型预测相对应的函数定义为Model.Evaluate()，框架代码如下：

X=GetSample()'获取输入变量的一组样本数据

Y=Predict(model, beta, X) '预测

return Y '返回预测结果

4)可靠性分析模块。该模块一方面需要集成各类可靠性算法(包括蒙特卡洛法、一次二阶矩法等)，另一方面需要与近似建模模块交互获得近似模型，并将其用于可靠性分析。该模块核心功能为可靠性分析，定义相应的计算函数为REL.Execute()，框架代码如下：

f=GetFunction()'获取功能函数基本形式

m=GetModel()'获取功能函数的近似模型

x=GetRandom()'获取随机变量向量

R=Solve(f, m, x) '进行可靠度计算

S=GetSensitivity()'进行灵敏度计算

4 算例

某引信MEMS安全保险机构设计方案如图4所示。弹丸发射后，当离心转速w达到30 000 rpm时，在离心力的作用下，离心保险解除。 弹丸继续飞行一定距离或时间后，根据有关传感器信息解除电保险(电保险闭锁簧片被推开)，滑块在离心力作用下，克服平面弹簧抗力向卡座位置滑动，直至锁入卡座。至此，传爆序列对正，引信处于待发状态。

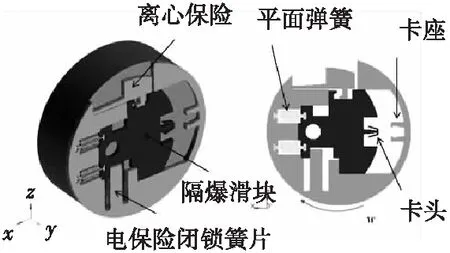
图4 引信MEMS安全保险机构示意图Fig.4 Schematic diagram of micro-fuze safety mechanism

通过仿真分析发现闭锁结构的卡头是该安全保险机构的薄弱环节，其与卡座完成闭锁的瞬间出现最大的弯曲应力，如图5所示。针对这一薄弱环节，综合考虑外部载荷、材料参数和尺寸参数等的影响，进行闭锁结构的可靠性仿真分析。

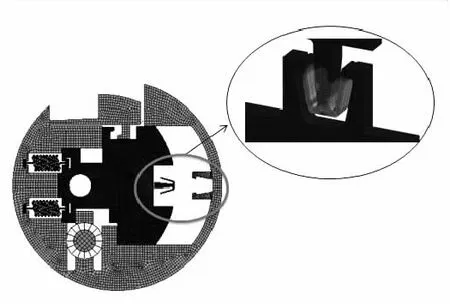
图5 闭锁结构仿真分析结果Fig.5 Locking structure simulation result

1)仿真工作流建立

建立如图6所示的单次仿真分析的工作流，为后续的试验设计等提供输入。其中采用HyperMesh软件进行仿真模型的建立，利用LS-Dyna进行闭锁过程的仿真分析，再由LS-PrePost读取仿真分析的结果数据。

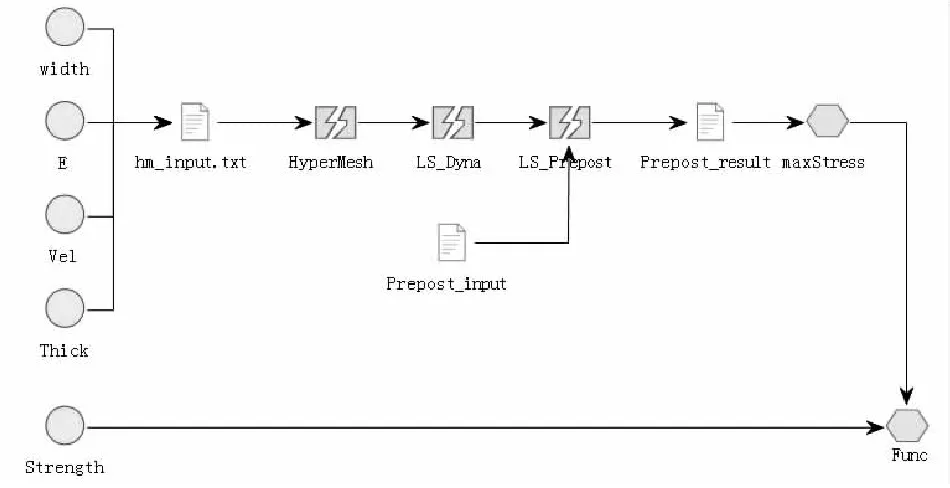
图6 闭锁结构仿真工作流Fig.6 Locking structure simulation workflow

图6中的各节点的说明见表2，其中冲击速度Vel由离心转速w和卡头质量换算而来；箭头表示仿真计算的顺序。

表2 仿真工作流各节点说明

2)试验设计与近似建模

首先，选择width 、E 、Vel 和thick为试验设计的输入变量， maxStress为试验设计的输出变量。输入变量的取值范围为[μ-3σ,μ+3σ]，其中μ和σ分别为随机变量的均值和标准差。采用三水平全因子(三水平为：μ-3σ,μ,μ+3σ)试验设计，在4个输入变量的情况下，共计需要进行81次仿真试验，总耗时约36 min。

然后，选择零阶多项式函数为回归模型的基函数、Gauss函数为相关性函数的核函数，进行Kriging模型的建立。取width=0.058 mm、thick=0.25 mm时，maxStress与E、Vel的Kriging曲面如图7所示(图中黑点为样本点)。

同时，增加五组样本数据用于检验Kriging近似模型，获得该模型的MSE(Mean Squared Error均方差)为1.790 5×10-4GPa，表明其具有较好的精度。

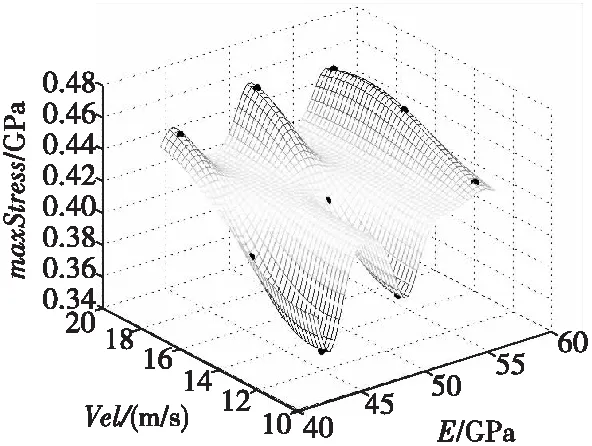
图7 maxStress与E、Vel的Kriging曲面Fig.7 Kriging surface of maxStress, E and Vel

3)可靠性分析

将概率表达式P(Strength-maxStress>0)中的maxStress替换为上述的Kriging模型，再利用一次二阶矩法进行可靠度和灵敏度的计算，结果分别如表3和表4所示。同时，为验证可靠度结果的正确性，基于式(4)所示的可靠性模型(不采用近似模型的情况)，采用蒙特卡罗法对进行抽样计算。为减少标准蒙特卡罗法的抽样次数(抽样次数106的情况下，总耗时将达305天)，采用文献[18]的重要抽样法以较少的抽样次数获得收敛的可靠度结果。

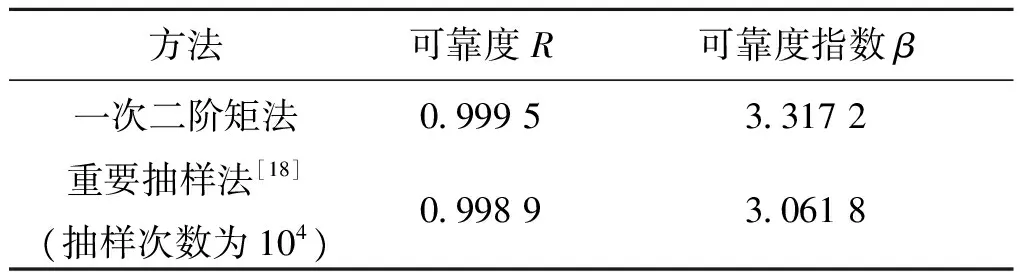
表3 可靠度结果

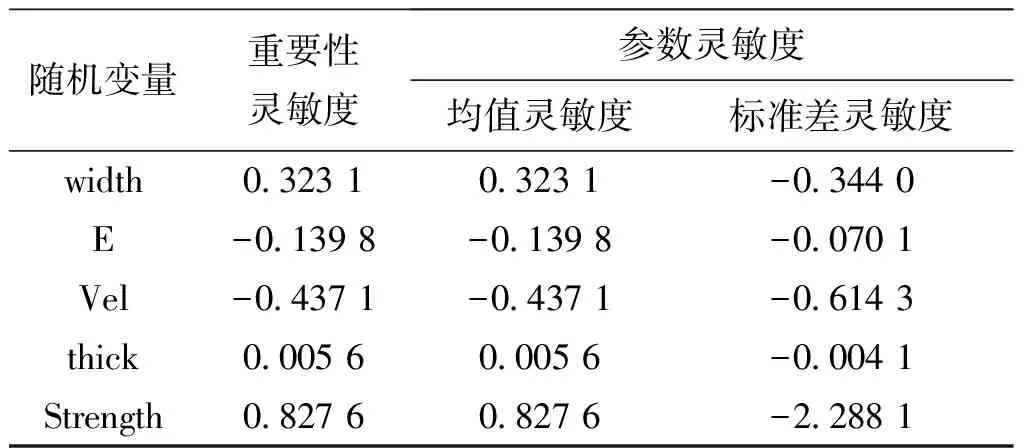
表4 灵敏度结果

(注：重要性灵敏度和均值灵敏度均已做归一化处理)

从表3可以看出，采用近似模型的分析方法可以获得较高精度的可靠度结果。在安全保险机构作用可靠度要求为0.99，且不考虑离心保险、电保险失效的情况下，闭锁结构可靠度满足要求。由于不考虑随机变量之间的相关性，表4所示的重要性灵敏度和均值灵敏度结果是一致的。其中，材料强度，以及闭锁结构宽度和厚度参数对于可靠性结果均呈“正”作用，即提高这些参数的均值，将有利于结构可靠性水平的提高；而材料和速度参数则呈“反”作用。且各变量的重要性水平可以从量化的数值大小进行比较。由标准差灵敏度结果可以看出，缩小各变量的标准差均有助于提高结构可靠度。

另外，在具体应用中，若单次有限元计算时间较长，那么采用蒙特卡罗法获得可靠性结果是不可行的。因此，在利用本文方法进行可靠性分析时，建议从两个方面保证结果的准确性：一是采用具有较高拟合精度的近似模型；二是采用经过验证的可靠度和灵敏度计算方法。

5 结 论

本文提出了基于有限元法的引信MEMS微结构可靠性仿真分析及实现方法。该方法可以在结构性能仿真分析的基础上，进一步开展量化的结构可靠性分析。其中，为实现可靠性分析程序对有限元软件工具的自动调用，以ANSYS软件为例给出CAE程序的集成方法和实现步骤；为降低可靠性分析程序对有限元仿真的调用次数，采用试验设计和近似建模相结合的方法，构建功能函数的近似函数。提出可靠性仿真实现的总体程序框架，给出各主要模块的功能及其主要函数的框架代码。实际算例表明了该可靠性仿真方法的可行性和实用性。

[1]景华, 牛兰杰, 宋永强. 小口径榴弹引信微机电安全系统设计与仿真方法[J]. 弹箭与制导学报, 2010, 30(2): 129-132.

[2]李晓杰, 牛兰杰, 翟蓉, 等. S型MEMS平面微弹簧垂直弹性系数[J]. 探测与控制学报, 2010, 32(1): 57-60.

[3]田中旺, 赵旭, 宋永强, 等. 改善强度的MEMS隔爆装置悬臂梁和卡头[J]. 探测与控制学报, 2011, 33(5): 1-4.

[4]孙诚诚, 牛兰杰, 赵旭, 等. 引信杆状弹簧质量块微机电离心保险装置[J]. 探测与控制学报, 2014, 36(1): 17-20.

[5]孙彩云，张康. 机电引信安保机构解除保险过程动态仿真[J].四川兵工学报, 2014(6):111-114.

[6]Rohit Pathak, Satyadhar Joshi. Optimizing reliability modeling of MEMS devices based on their application [J]. Work Journal ofModeling and Simulation, 2011(2): 139-154.

[7]Adam Martowicz, Tadeusz Uhl. Reliability- and performance-based robust design optimization of MEMS structures considering technological uncertainties [J]. Mechanical Systems and Signal Processing, 2012, 32: 44-58.

[8]Viviana Mulloni, Francesco Solazzi, Giuseppe Resta, etc. RF-MEMS switch design optimization for long-term reliability [J].Analog Integrated Circuits and Signal Processing, 2014, 78(2): 323-332.

[9]秦权, 林道锦, 梅刚. 结构可靠度随机有限元-理论及工程应用[M]. 北京：清华大学出版社, 2006.

[10]Akira Todoroki，Tetsuya Ishikawa．Design of experiments for stacking sequence optimizations with genetic algorithm using response surface approximation [J]．Composite Structures，2004，64：349-357.

[11]Sei-Ichiro Sakataa, Fumihiro Ashidaa, Masaru Zakob. Approximate structural optimization using kriging method and digital modeling technique considering noise in sampling data [J]. Computers & Structures, 2008, 86(13): 1477-1485.

[12]Soren N Lophaven, Hans Bruun Nielsen, Jacob Sondergaard. DACE A Matlab Kriging Toolbox：Report IMM-REP-2002-13[R] Informatics and Mathematical Modeling， Technical University of Denmark, 2002. http://www.imm.dtu.dk/～hbn/dace/.

[13]Irfan Kaymaz. Application of kriging method to structural reliability problems [J]. Structural Safety, 2005, 27: 133-151.

[14]Ditlevsen O, Madsen HO. Structural Reliability Methods [M].West Sussex, England: John Wiley & Sons Ltd., 2007: 94-101.

[15]Melchers RE, Ahammed M. A fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Computers & Structures, 2004, 82: 55-61.

[16]Wu YT, Sitakanta M. Variable screening and ranking using sampling-based sensitivity measures[J]. Reliability Engineering & System Safety, 2006, 91: 634-47.

[17]Jensen H A, Mayorga F, Papadimitriou C. Reliability sensitivity analysis of stochastic finite element models [J]. Computer Methods in Applied Mechanics and Engineering, 2015, 296: 327-351.

[18]Frank Grooteman. Adaptive radial-based importance sampling method for structural reliability [J]. Structural Safety, 2008, 30: 533-542.

ReliabilitySimulationMethodforMEMSMicro-structureinFuze

TU Hongmao1,2, SUN Zhili1, JI Guangzhen3, LIU Qin1,2

(1. College of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China； 2. Ordnance Science and Research Academy of China, Beijing 100089, China)

Reliability simulation method for MEMS micro-structure in fuze and its implementation details for further quantitative reliability assessment based on the corresponding performance simulation were proposed in this paper. By taking ANSYS as an example, the CAE program integration method and its implementation procedure were presented to facilitate the finite element tools utility during reliability simulation. It used design of experiment method and approximation modelling to reduce the number of times of finite element simulations in the whole reliability analysis procedure. Then, basic principles of reliability and sensitivity calculation issues were given. Programme framework for the reliability simulation method and its main code block were also presented. An engineering example demonstrated the feasibility and practicality of the proposed method were feasible and practical.

fuze reliability; MEMS micro-structure; reliability simulation; finite element method; reliability

2017-01-21

:国防技术基础项目资助(Z092014B001)

:涂宏茂(1981—)，男，福建泉州人，博士研究生，副研究员，研究方向：MEMS可靠性。E-mail：bjthm@126.com。

TB114.3

：A

：1008-1194(2017)04-0005-07