基于多点故障行波检测的改进分布式故障测距方法研究
王 博, 谷昌瑞, 吉晓筱, 王 俊
(1. 扬州科宇电力有限公司,江苏 扬州 225000;2. 南京理工大学自动化学院,江苏 南京 210094)
基于多点故障行波检测的改进分布式故障测距方法研究
王 博1, 谷昌瑞1, 吉晓筱2, 王 俊2
(1. 扬州科宇电力有限公司,江苏 扬州 225000;2. 南京理工大学自动化学院,江苏 南京 210094)
在对高压输电线路进行故障定位的方法中,行波法因其具有较好的抗干扰性和较高的测距精度而受到国内外关注。传统的行波测距法在输电线路发生多点故障时行波混叠可能引起测距误差增大,难以实现准确定位。针对上述问题,文中通过分析输电线路行波的波动过程及其传输特性,给出了常规行波测距算法的适用范围,在此基础上,提出了改进的分布式行波测距方法。该方法通过获取故障后多个测量点的行波到达时刻,拟合出行波波头传输特性曲线,然后利用该曲线去求解故障点的具体位置。最后运用PSCAD构建500 kV输电线路仿真模型对文中的方法进行仿真,验证了其有效性。
高压输电线路; 故障测距; 分布式行波测距; 多点故障; PSCAD
1 引言
阻抗法和行波法是用于测距的两类方法。其中行波法依据输电线路故障时产生的行波传播特征(传播速度、路径、时间等)来进行测距[1]。目前,行波测距法主要包括A-F这6类[2],其中A,C,E和F型利用的是行波到达同一个检测点的时间差,属于单端测量方法,B和D型则是利用故障行波到达不同检测点所用时间的不同来检测,属于双端测量方法[3]。
行波测距的准确性依赖于突变信号检测算法来标定行波波头的到达时刻,常见的波头检测方法有小波变换[4]、希尔伯特-黄变换[5]和数学形态学[6]等方法。其中,小波变换因其多分辨率、且在时、频域都具有表征信号局部特征的能力等优点得到了广泛采用。在行波测距中,通常使用小波变换模极大值与信号突变点相对应的方法来检测波头[7]。
传统的行波测距法在线路单点故障时具有较好的准确性,但是当发生多点故障时,由于行波混叠可能引起传统的行波测距法测距误差增大,难以实现准确定位[8]。
针对上述问题,文中通过分析输电线路行波的波动过程及其传输特性,给出了常规行波测距算法的适用范围,在此基础上,针对传统行波测距法的局限性,提出改进的分布式行波测距方法。该方法通过获取故障后多个测量点的行波到达时刻,拟合出行波波头传输特性曲线,然后利用该曲线去求解故障点的具体位置。最后,运用PSCAD构建500 kV输电线路仿真模型对文中的方法进行仿真,验证了其有效性。
2 行波测距法的适应性分析
2.1 单端行波测距原理分析
利用单端行波检测的测距方法中,根据故障测距时选用的反射波的不同,可将单端行波测距分为基于故障点反射波的单端行波法和基于对端母线反射波的单端行波[9]。其主要原理都是利用行波第一次到达测量端与其从故障点反射回的时间差进行故障距离的计算。
基于故障点反射波的单端行波法是通过检测初始行波与该行波经故障点反射后到达母线端的时间差,来实现测距,运用该方法进行测距的原理示意图如图1所示。该方法适用于故障点处反射系数较大(即故障电阻较小)的情况[10]。

图1 利用故障点反射波的单端行波测距原理示意图Fig.1 Single-ended traveling wave fault location using its reflected waves
设行波传播的正方向为由母线到故障点,则故障初始行波波头到达测量端时的时刻为TM1,其为反向行波,该行波经母线反射后,传播到故障点经再次反射传播回母线,设再次到达母线的时间为TM2。则故障距离为:

(1)
式(1)中:XM为故障点与M端母线的距离;v为行波传播的速度。
2.2 双端行波测距原理分析
双端行波测距方法的原理:输电线路故障时发出的行波信号,由于距两端距离的不同,从而使得到达线路两端的时间也不一样。双端行波测距就是利用这个时间的差值来计算出故障点位置的[11]。其测距原理示意图如图2所示。

图2 双端行波测距原理示意图Fig.2 Double-ended traveling wave fault location
图2中,在高压输电线路的两端即M,N端均装设行波测量装置,故障发生在F点处,设L为线路的全长,TM与TN分别为故障产生的行波波头到达M,N端的时间,则根据图示可得:
(2)
式(2)中:XM为故障点距离M端母线的距离;XN为故障点距离N端母线的距离;v为行波波速。
则可以得到:
(3)
双端行波测距原理简单,且由于其仅需识别两端检测到的第一个波头到达时刻,无需对行波的折反射信号进行识别,而具有较高的可靠性。
2.3 传统行波测距方法的适应性
传统行波测距法的研究主要从波速、信号分析、奇异点时刻获取以及对有分支线路、光纤电缆混合线路的测距方法等方面[12,13]进行了深入的研究,但大都针对发生单处故障进行研究。高压长距离输电线路由于途径的很多气候环境比较恶劣的地区,故障类型相对也较为复杂,一条输电线路很可能会发生不止一处故障[14],当输电线路上发生多重故障时,将会产生复杂的行波过程,且以2处故障为例,对传统行波测距法的适应性进行分析。输电线路上发生2处故障的示意图如图3所示。

图3 输电线路两处故障示意图Fig.3 Two faulty transmission lines

(5)
根据式(5)可以得到M端测量点行波通过折反射到达的时间与波头首次到达的时间差,各时间差为:
(6)
运用单端行波测距法时,需要检测初始行波浪涌到达母线端时刻与故障点反射波(或对端母线反射波)到达时刻的时间差来实现测距。因此使用单端行波测距就必须准确获取待测距故障点的初始行波和反射行波到达测量端的时间[15]。初始行波浪涌到达时刻为故障点F1正向行波首次到达时间,故障点F1的位置Lx1的准确测量依赖于母线反射波到达时刻的测量,因此只有当不等式条件(7)成立时,单端行波测距才能测量出故障点F1的位置。
(7)
由上可以看出,当故障点距离Lx1,Lx2满足Lx1≤Lx2,且Lx1≤(2/3)L-(1/3)Lx2时运用单端行波测距可以准确地测得故障点F1的故障距离。
对于双端行波测距,其测量的是线路两端M,N端的信号突变量即行波到达时刻,设故障发生在t0时刻,则故障行波传输到输电线路M端的时间为t1,传输到N端的时间为t2,该传输时间满足的关系为:
(8)
由方程组只能求得Lx1+Lx2的距离,对于线路发生两处故障的情况下,双端行波测距必须在单端行波测距测得其中一个故障后,再测出另一个故障距离。
综上可知,当线路发生2处故障时,由于线路上叠加了2个行波波头从线路不同地点朝两端传输,同时在2个故障点都将发生行波的折反射,传统行波测距方法将面临一定的局限性。
3 基于分布式行波检测的改进故障测距方法
3.1 改进方法原理
故障时产生的行波波头向两端传播,在时刻t1,两端波头达到的位置距离M端的距离为XM(t1)、距离N端的距离为XN(t1),同理t2时刻,故障行波波头分别到达XM(t2),XM(t2)。以此类推则可以得到以时间为横坐标的曲线XM=m(t)和XN=n(t)。2条曲线分别描述了各时刻故障行波波头到达的位置,其描述了行波波头在线路上的传播特性,称为行波波头传播特性曲线[16]。如图4所示。

图4 行波波头传播特性曲线原理图Fig.4 Propagation characteristics of traveling wave head
根据故障点两端行波波头的传播特性曲线可以确定故障点的具体位置,具体流程图如图5所示。
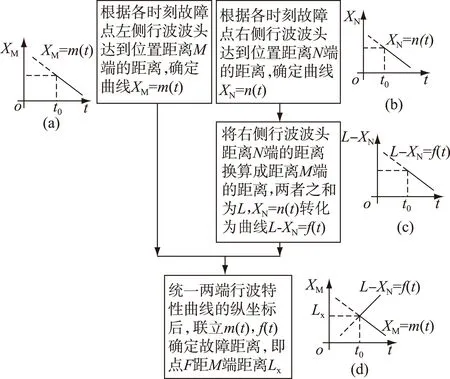
图5 行波波头传播特性曲线和故障位置求解示意图Fig.5 Propagation characteristics of traveling wave head and fault location solution
图5中t0时刻为故障时刻。由于t0时刻前的传播特性曲线实际并不存在,故用虚线表示。图5中的(a)图纵坐标XM是故障点左侧行波波头距离M端的距离;图5中(b)图的纵坐标XN则是故障点右侧行波波头距离N端的距离。要统一两曲线的纵坐标,即都以行波波头距M端的距离为纵坐标,需要对图5中(b)图的纵坐标进行转换,见图5中(c)图。则XM=m(t)与曲线XN=n(t)的交点就表示故障发生的时刻和位置,见图5中(d)图。
由图5中(d)图可知,XM=m(t)和L-XN=f(t) 两曲线交点所在位置的纵坐标就是故障点距输电线路M端的距离,其横坐标是故障时刻t0。
利用行波波头传播特性曲线求解故障位置消除了波速因素对传统测距方法的精度造成的影响,同时针对多点故障的情况,可以通过分别构建不同故障点的行波波头传播特性曲线来求解各自的位置,从而解决了传统测距方法在多处故障时不适用的问题。但是如何获取行波波头传播特性曲线是需要重点解决的问题。对此,文中提出了基于分布式行波检测的改进故障测距方法。该方法通过在输电线路沿线的不同位置安装多组故障信号检测装置,利用各装置获取检测点处行波波头到达的时刻,然后通过拟合的方法来构建行波波头在该输电线路上的传播特性曲线,从而定位故障发生的位置。
3.2 改进方法在2处故障时的具体应用
设线路MN中设有A1,A2,A3,…An个测量点,当线路发生2处故障时,故障点分别为F1和F2,假设F1位于测量点Ai和Ai+1间,F2位于测量点Aj和Aj+1间,且i 图6 分布式故障测距检测系统示意图Fig.6 Distributed traveling wave fault location system (9) Aj+1,Aj+2,…An的各个故障行波到达时间顺序也是惟一确定的,其时序关系为: (10) 对于2故障点之间的检测点Ai+1,…Aj,根据2故障点的位置分为3种情况讨论,即故障发生位置处于同一分段中,故障发生在相邻的分段中,故障发生在不相邻的分段中。 (1) 当i=j时,分布式故障测距检测系统示意图如图7所示。 图7 分布式故障测距检测系统示意图(i =j)Fig.7 Distributed traveling wave fault location system(i =j) 对于测量点有Ai+1=Aj+1,该测量点行波到达时间满足式(10)。构建行波波头传输特性曲线,如图8所示。 图8 i=j时的行波波头传播特性曲线Fig.8 Propagation characteristics of traveling wave head while i=j (2) 当i+1=j时,分布式故障测距检测系统示意图如图9所示。 图9 分布式故障测距检测系统示意图(i=j -1)Fig.9 Distributed traveling wave fault location system(i=j -1) 此时,对于测量点Ai+1有Ai+1=Aj,且点Ai+1初始行波到达时间顺序为: 由此可以根据测量点Ai,Aj+1检测到的第一个行波的时间判断测量点Ai+1的行波时序。确定行波波头传输特性曲线,如图10所示。 图10 i +1=j时的行波波头传播特性曲线Fig.10 Propagation characteristics of traveling wave head while i +1=j 图10中直线l1为L-XN=f2(t);直线l2为L-XN=f1(t);直线l3为XM=m2(t),直线l4为XM=m1(t)。点Lx1,Lx2分别为故障点F1,F2距M端距离。 此外,在构建行波波头传播特性曲线前,需要先确定2个故障点的故障区间。关于故障区间判断,研究学者提出了较多的方法[17,18]。文中采用了文献[19]所提出的利用工频故障电流之间的偏离度和波头到达时间来判断故障区间的方法,以确定故障区间。 该方法利用行波到达时刻来初步判断故障可能出现的区段,同时利用输电线路上各点电流之间偏离度来确定线路故障的具体区段。在得到故障区间2故障点的位置关系后,利用前述的结论,拟合出各自的行波波头传播特性曲线,就可以实现各故障点的准确定位。 4.1 仿真条件 在PSCAD中搭建500 kV双端供电系统,仿真模型如图11所示。其中,左侧电源系统阻抗为9.19+j52.1 Ω,右侧电源的系统阴抗为8.19+j42.11 Ω,线路MN全长为300 km,且对输电线路采用分布参数的仿真模型。仿真时间0.3 s,故障起始时刻0.2 s,故障持续时间0.1 s。小波变换采用db小波对分解过的信号进行模极大值变换以获得行波信号的突变信息[20]。 图11 分布式行波测距系统仿真模型图Fig.11 Simulation model of the distributed traveling wave fault location system 在仿真过程中,模拟不同故障类型包括模拟单相接地、相间短路、两相接地短路和三相短路等的故障,同时在不同过渡电阻、不同故障距离对故障测距的影响,具体测距流程如下: (1) 设置故障类型、故障距离等参数,利用PSCAD进行高压输电线路故障情况仿真,获取测量点故障信息。 (2) 取故障前后一段时间的数据,利用matlab对采样数据利用小波变换进行处理,并对得到的故障高频分量提取模极大值,得到各检测点故障行波信号。 (3) 根据分布式行波测距原理,利用获取的故障信号拟合行波波头传输特性曲线,从而求出故障的距离。 (4) 分析利用基于分布式行波测距算法测得的故障距离,分析该方法测距的故障距离与实际故障距离,并将其同常规测距算法测得的结果进行比较。 4.2 单处故障仿真分析 以距离M端70 km处发生A相接地故障为例,PSCAD仿真系统中故障发生在0.2 s时刻。 图12为M端测量点A1的电流仿真波形,对该电流I1进行相模变换后,然后取变换后的线模分量进行小波变换取模极大值,模极大值图如图13所示。 图12 测量点A1的电流波形Fig.12 Current wave at measuring point A1 图13 测量点A1的电流波形取模极大值结果Fig.13 Modulus maxima of current wave at measuring point A1 对于检测点A1,其第一个模极大值对应的时刻为0.200 232 s。同理可得到检测点A2,A3,A4的电流仿真波形及其模极大值图,从而可以得到各个检测点第一个极大值对应的时间分别为0.200 098 s,0.200 433 s,0.200 768 s。计算故障的行波波头特性曲线为: (11) 又由于Xm=L-Xn,则可得Xm=69.99 km,从测距结果看,距M端69.99 km处故障测得的故障距离为69.99 km,结果具有很高的精度,符合测距要求。 分别设置故障点在10 km,70 km,130 km和270 km处,行波波速取2.96×108m/s。通过分布式行波测距的测距结果如表1所示。 表1 单处故障时的分布式行波测距结果Table 1 Results of distributed traveling wave fault location when single fault happens 由表1可知,运用基于小波变换的分布式行波测距对故障位置测量有着很高的测量精度,同时对故障位置、故障类型和过渡电阻都有一定的适应性,并且检测误差基本均在0.1%以内,满足工程需要。其较常规行波测距方法而言,由于消去了波速对故障测距的影响,具有更高的测量精度。 4.3 2处故障仿真分析 系统发生2处故障时的仿真模型如图14所示。依然设在输电线路上距离M端40 km和170 km处发生了A相接地故障,PSCAD仿真系统中故障发生在0.2 s时刻。 图14 系统发生2处故障的仿真模型图Fig.14 Simulation model of the system with two faults 图15为M端测量点A1的电流仿真波形。对该电流I1进行相模变换后,然后取变换后的线模分量进行小波变换取模极大值,模极大值图如图16所示。 图15 测量点A1的电流波形Fig.15 Current wave at measuring point A1 图16 测量点A1的电流波形模极大值Fig.16 Modulus maxima of current wave at measuring point A1 对于检测点A1,其第一个模极大值对应的时刻为0.200 232 s。同理可得检测点A2,A3,A4的电流仿真波形及其模极大值图,各个检测点第一个极大值对应的时刻分别为0.200 100 s,0.200 200 s,0.200 534 s。其中检测点A3检测到的第二个模极大值对应的时间为0.200 434 s,结合故障区间的判别结果,该模极大值点对应着故障F1的反向行波到达检测点A3的时间。则故障的行波波头特性曲线为: (12) 式(12)中:Xm1=L-Xn1,Xm2=L-Xn2,且Xm1,Xm2分别为故障点F1,F2距M端的距离。 对式(12)的方程组进行求解,可得2故障点距M端的距离分别为70.06 km,140.12 km。 分别设置故障点在70 km,140 km;65 km,240 km;140 km,260 km;50 km,80 km;150 km,170 km;240 km,275 km处。通过双端行波测距法的测距结果如表2所示。 由表2可知,运用基于小波变换的双端行波测距对故障位置、故障类型和过渡电阻都有一定的适应性,并且检测误差基本小于0.3%,满足工程测试的需求。 表2 2处故障时的分布式行波测距结果Table 2 Results of distributed traveling wave fault location when two faults happen km 文中针对现有的常规故障测距方法在线路发生两处故障时准确度较低的问题,提出了一种基于分布式改进的行波测距方法。该方法避开了对输电线路中行波波速值的依赖,具有更强的抗噪声干扰特性和更高的测量精度。仿真结果表明,该行波测距方法对输电线路不同位置的故障均能实现高精度的故障测距。 [1] 黄 震, 江泰廷, 张维锡, 等. 基于双端行波原理的高压架空线-电缆混合线路故障定位方法[J]. 电力系统自动化, 2010 34(14): 88-91. HUANG Zhen,JIANG Taiting,ZHANG Weixi,et al. A fault location method for high-voltage overhead lines combined with underground power cables based on double-ended travelling wave principle[J]. Automation of Electric Power System,2010 34(14): 88-91. [2] 谭文展, 关均康. 基于北斗卫星定位系统的高压输电线路双端故障定位研究[J]. 电工技术, 2008 (5): 27-29. TAN Wenzhan,GUAN Junkang. Research on double end fault location technology of high voltage transmission line base on beidou satellite positioning system.[J]. Electrician technology,2008 (5): 27-29. [3] 季玉中. 关于输电线路的故障测距方法的探讨[J]. 电子世界, 2013, (20): 44-45. JI Yuzhong. Discussion on fault location method of power transmission line[J]. Electronic World, 2013, (20): 44-45. [4] 林 圣, 何正友, 陈 鉴, 等. 基于行波时频特征的单端故障测距方法[J]. 电网技术, 2012, 36(1): 258-264. LIN Sheng,HE Zhengyou,CHEN Jian, et al. A single terminal fault location method based on time-frequency characteristic of traveling wave[J]. Power System Technology, 2012, 36(1): 258-264. [5] 于玉泽, 覃 剑, 李功新, 等. 电缆-架空线混合线路故障测距方法综述[J]. 电网技术, 2006, 30(17): 64-69. YU Yuze,TAN Jian,LI Gongxin,et al. A survey on fault location methods for hybrid transmission lines consisting of power cables and overhead lines[J]. Power System Technology, 2006, 30(17): 64-69. [6] 束洪春, 程春和, 赵文渊, 等. 形态学与HHT检测相结合的行波波头准确标定方法 [J]. 电力自动化设备, 2009, 29(7): 1-7. SHU Hongchun,CHENG Chunhe,ZHAO Wenyuan,et al. Accurate traveling-wave front detection based on morphology and HHT[J]. Electric Power Automation Equipment, 2009, 29(7): 1-7. [7] 陈学伟. 500 kV输电线路精确故障定位技术研究[D]. 济南:山东大学, 2013. CHEN Xuewei. Research on accurate fault location technology for 500 kV transmission lines[D]. Jinan: Shandong- U-n-i-v-e-r-sity, 2013. [8] 何军娜, 陈剑云, 艾颖梅, 等. 电力系统行波测距方法及其发展[J]. 电力系统保护与控制, 2014, 42(24): 148-154. HE Junna,CHEN Jianyun,AI Yingmei,et al. Fault location methods based on traveling wave theory for power system and its development[J]. Power System Protection and Control, 2014, 42(24): 148-154. [9] BRAHMA S M, GIRGIS A. Fault location on a transmission line using synchronized voltage measurements[J]. Power Delivery, IEEE Transactions on, 2004, 19(4): 1619-1622. [10] DE MORAIS-PEREIRA C E, ZANETTA L C. Fault location in transmission lines using one-terminal postfault voltage data[J]. Power Delivery, IEEE Transactions on, 2004, 19(2): 570-575. [11] 刘亚东, 盛戈皞, 孙 岳, 等. 基于故障电流信息综合分析的分布式单相接地故障测距方法[J]. 电网技术, 2012, 36(8): 87-94. LIU Yadong,SHENG Geao,SUN Yue,et al. A distributed fault location algorithm for single-phase ground fault by comprehensive analysis on fault current information[J]. Power System Technology, 2012, 36(8): 87-94. [12] 李 勇. 基于暂态电流行波的输电线路继电保护及故障定位系统研究[D]. 沈阳:东北大学, 2012. LI Yong. Research of transmission line relay protection and fault location system based on transient current travelling waves[D]. Shenyang: Northeastern University, 2012. [13] 刘洪正, 高厚磊, 韩志骏, 等. 输电线路加权数据融合故障测距算法研究[J]. 电力系统保护与控制, 2014, 42(15): 15-20. LIU Hongzheng,GAO Houlei,HAN Zhijun,et al. Transmission line fault location algorithm based on weighted data fusion[J]. Power System Protection and Control, 2014, 42(15): 15-20. [14] 王利平, 王晓茹, 王 伟, 等. 输电线路加障测距实用算法研究[J]. 电力系统保护与控制, 2014, 42(16): 24-30. WANG Liping, WANG Xiaoru, WANG Wei, et al. Study of faultslocation algorithm on power transmission lines[J]. Power System Protection and Control, 2014, 42(16): 24-30. [15] 周 鑫, 吕飞鹏, 吴 飞, 等. 基于小波变换的T型线路故障测距新算法[J]. 电力系统保护与控制, 2010 38(2): 8-11. ZHOU Xin,LYU Feipeng,WU Fei,et al. A new fault location method for T-connection transmission lines based on wavelet transform[J]. Power System Protection and Control, 2010 38(2): 8-11. [16] 刘亚东. 输电线路分布式故障测距理论与关键技术研究[D]. 上海:上海交通大学, 2012. LIU Yadong. Distributed fault location theory and the key technologies for transmission line[D]. Shanghai: Shanghai Jiao Tong University, 2012. [17] 朱 翔, 解 大, 高 强, 等. Db8小波在电力系统谐波分析中的应用[J]. 电力科学与技术学报, 2011, 26(2): 67-71. ZHU Xiang,XIE Da,GAO Qiang,et al. On the application of analyzing power system harmonics using Db8[J]. Journal of Electric Power Science and Technology, 2011, 26(2): 67-71. [18] 李小鹏, 何正友, 武 骁, 等. 计及故障测量装置失效的输电网固有频率故障定位方法[J]. 电网技术, 2013, 37(5): 1217-1222. LI Xiaopeng,HE Zhengyou,WU Xiao,et al. Natural f-r-e-q-u-e-n-cies based fault location method for transmission network considering measurement device invalidation[J]. Power System Technology, 2013, 37(5): 1217-1222. [19] 逯怀东, 许 磊, 刘宗杰, 等. 电缆-架空线混合线路故障行波定位及自适应重合闸控制[J]. 电力科学与技术学报, 2013, 28(4): 31-35. LU Huaidong, XU Lei, LIU Zongjie,et al. New method of traveling wave fault location and adaptive reclosing for cable-overhead mixed lines[J]. Journal of Electric Power Science and Technology, 2013, 28(4): 31-35. [20] 郑 州, 吕艳萍, 王 杰, 等. 基于小波变换的双端行波测距新方法[J]. 电网技术, 2010, 34(1): 203-207. ZHENG Zhou,LYU Yanping,WANG Jie,et al. A new two-terminal traveling wave fault focation method based on wavelet transform[J]. Power system technology, 2010, 34(1): 203-207. (编辑徐林菊) Research on Improved Distributed Fault Location Method based onMulti-point Fault’s Traveling Wave Detection WANG Bo1, GU Changrui1, JI Xiaoxiao2, WANG Jun2 (1. Yangzhou Keyu Electric Power Co. Ltd., Yangzhou 225000, China;2. Nanjing University of Science & Technology, Nanjing 210094, China) In traditional locating fault methods using on high voltage lines, the traveling wave method has drawn attention at home and abroad with better anti-interference and higher ranging accuracy. However, when multiple faults occur on the transmission line, its error will become large because of traveling wave’s overlap. In order to solve this problem, this paper proposes the improved distributed traveling wave fault location method after analyzing the transmission characteristics of traveling wave on transmission line in fluctuation process and conventional method’s limitations. Firstly, this improved method fits the characteristic curve of the traveling wave head using its arriving time which reaches the multiple measurement points. And then, it uses the curve above to solve the specific position of the fault occurs. Finally, the effectiveness of this method is verified by using PSCAD to construct and simulate the 500 kV transmission line model. HV transmission lines; fault location; distributed traveling wave fault location; multiple faults; PSCAD 王 博 2017-04-22; 2017-05-28 TM726 :A :2096-3203(2017)05-0120-08 王 博(1981—),男,江苏南京人,高级工程师,从事智能化电器以及配网自动化的研究工作(E-mail:4832455@qq.com); 谷昌瑞(1985—),男,江苏扬州人,工程师,从事智能化电器以及配网自动化的研究工作(E-mail:278700738@qq.com); 吉筱筱(1991—),女,江苏盐城人,工程 师,研究方向为电力系统继电保护(E-mail:937818260@qq.com); 王 俊(1992—),男,江苏南京人,硕士研究生,研究方向为微电网保护(E-mail:535462103@qq.com)。




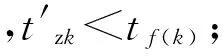
4 仿真验证

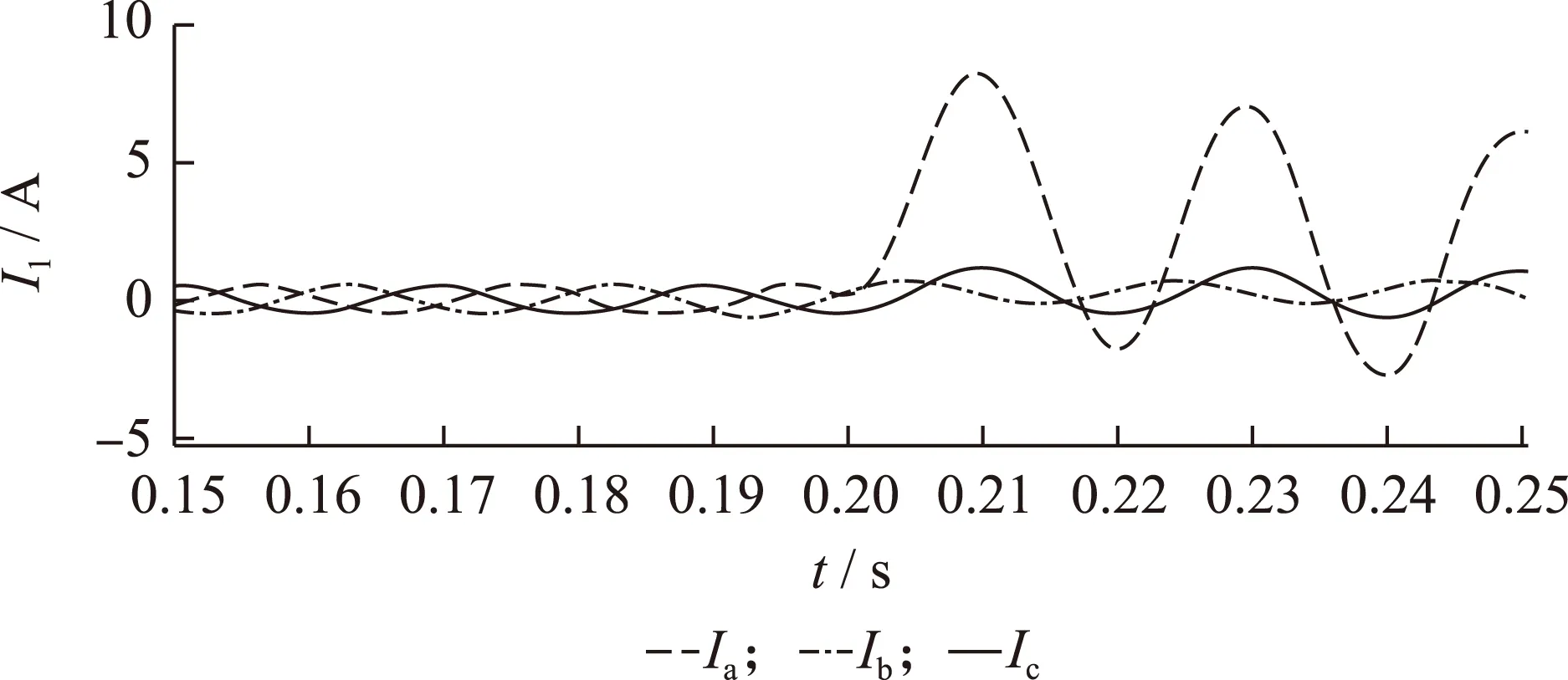



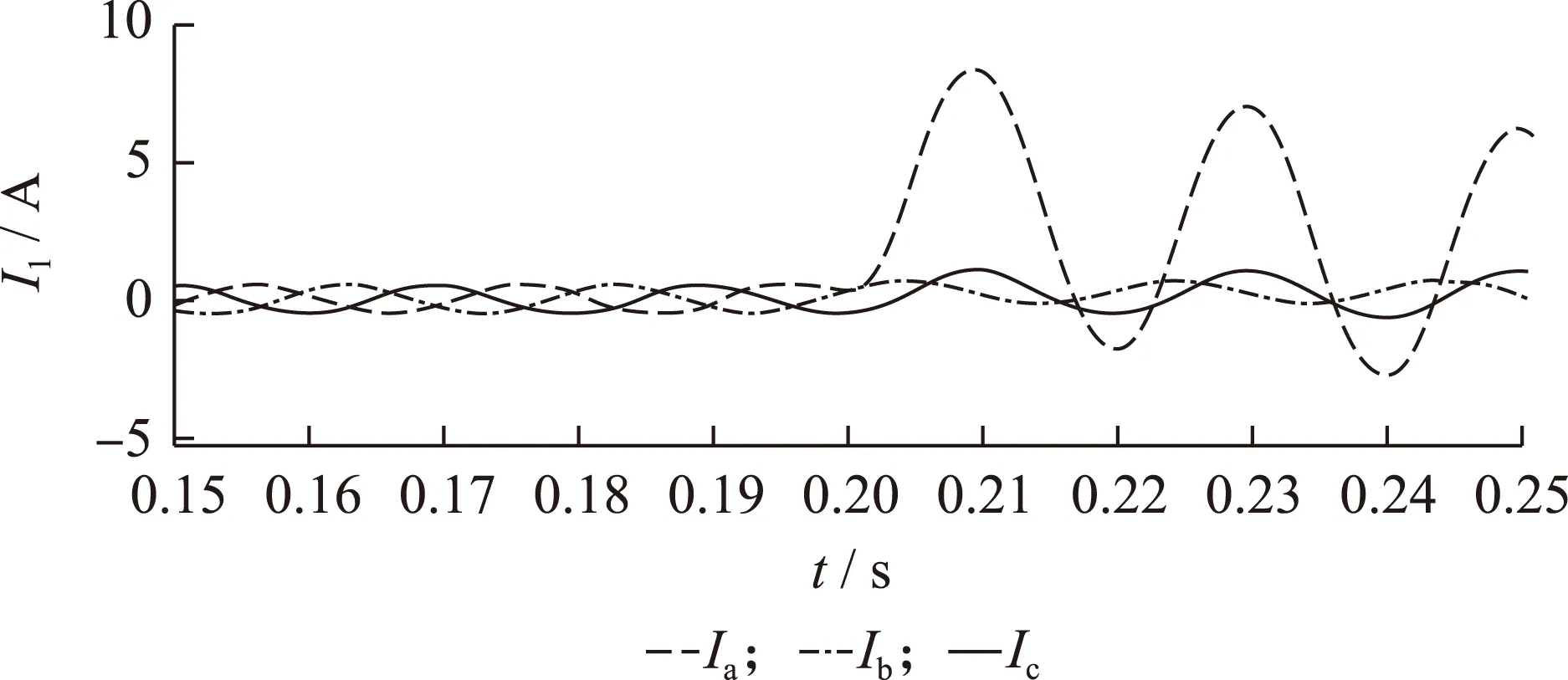


5 结论


