自步学习在确定含水层参数中的应用

杨陈东,常安定,张 明

(1.西安航空学院理学院,陕西 西安 710077; 2.长安大学理学院,陕西 西安 710061)

自步学习在确定含水层参数中的应用

杨陈东1,常安定2,张 明1

(1.西安航空学院理学院,陕西 西安 710077; 2.长安大学理学院,陕西 西安 710061)

通过分析受到误差影响的抽水试验数据进行含水层估计,为含水层参数估计提供方法支持。以机器学习领域的自步学习方法为基础,构造了基于差分进化算法优化的自步学习方法,并将其应用到含水层参数确定中；在不同误差水平下,与其他方法进行对比试验。结果表明,在不同误差水平下,估计参数值与传统估计值之间以及仿真数据与原始数据之间均保持较小差异；基于抽水试验数据估计含水层参数的自步学习方法估计结果有效可靠,算法对误差的稳定容错性强。

水资源;含水层参数;抽水试验;自步学习;差分进化算法

在地下水资源评价与开发过程中,导水系数和储水系数等含水层参数是非常重要的基本数据,分析非稳定流抽水试验数据是确定含水层参数的重要途径之一。针对Sushil方法及直线图解法等[1-2]传统方法的局限性,将智能优化算法应用在确定含水层参数中,表现出一定的优越性[3-4],由于此类方法目标函数均采用最小二乘形式,这里将其统称为最小二乘方法。最小二乘方法均没有考虑实测数据的误差,事实上,误差是普遍存在的,数据在获取和传输过程中都存在误差污染的可能。当数据存在较大误差时,以最小二乘为目标函数的优化问题将严重偏离真实结果。因此,如何从含有比较严重的误差和奇异值的抽水试验数据中,确定更加有效、可靠的含水层参数,具有十分重要的意义。

受人类学习原则启发,2009年,Bengio等[5]提出一种全新的机器学习框架,其核心思想是逐渐将样本序列加入学习,简单样本先学习,较难的样本后学习。这种先易后难的学习策略对应于人类(及其他动物)在不同成长阶段学习不同难度知识的规律。2010年,Kumar等[6]提出了自步学习(self-paced learning,SPL),并将其应用到潜变量模型中。之后SPL框架被广泛应用到各个领域[7-10]。2015年,Zhao等[11]将选择样本中的二值权值推广到实值权重,使得学习方式更加灵活。本文构造基于差分进化(differential evolution, DE)算法优化的自步学习模型,并将其应用于含水层参数确定中，可为含水层估计提供方法支持。

1 自步学习

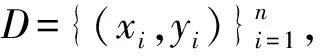
(1)

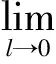
(2)

式中引入参数γ>0来控制用于选取样本的权重的强度。

利用泰斯公式及其近似表达式[4],可计算在含水层中距抽水井距离为r处的水位降深sei。在应用自步学习时,要求待估计的参数值能使下式表示的目标函数达到最小：

(3)

式中：soi为抽水开始后第i个时刻观察到的实际水位降深;θ为待估参数。

2 DE算法优化的自步学习模型

2.1 基本思想

DE算法是一种全局并行优化算法,具有记忆个体最优解和种群内部信息共享的特点[13],这种算法主要包括交叉、变异和选择等操作算子。其基本思想是运用当前种群个体的差分变异和交叉重组得到的中间种群,然后基于贪婪选择策略对父代种群和中间种群中的个体进行选择操作得到具有更佳适应度的子代个体。

将式(3)作为目标函数,对待估参数向量θ=(T,μ)、样本的权重(v1,v2,…,vn)进行编码得到(θ,v1,v2,…,vn)作为决策变量,利用DE算法进行优化。同时,年龄系数随着迭代次数增加而不断增大。这使得在迭代前期,算法结果不精确的情况下,算法选择简单样本进行训练;在迭代后期,算法将考虑更多更为复杂的样本,从而趋向成熟。

2.2 算法步骤及流程

步骤1:初始化种群规模N、交叉因子C、输入求解参数的上界和下界、 最大迭代次数kmax以及满足精度要求的迭代次数k。

步骤2:利用式(3)计算各个体的适应度fi及其对应位置gi,从其中确定全局最优适应度f及其对应位置g。

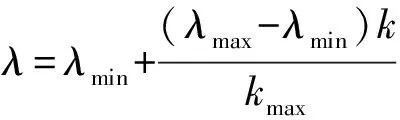
步骤4:由DE算法得到变异个体mi,k+1,试验个体ui,k+1 和下一代个体xi,k+1。计算并比较ui,k+1 与xi,k+1 相应的适应度值,将新的最优位置赋给xi,k+1;并且在新的历史最优位置中确定全局最优位置g。

步骤5:如果满足终止条件,则停止迭代;否则k=k+1,转向步骤3。

步骤6:输出全局最优适应度f及其相应位置g。

算法流程图如图1所示。

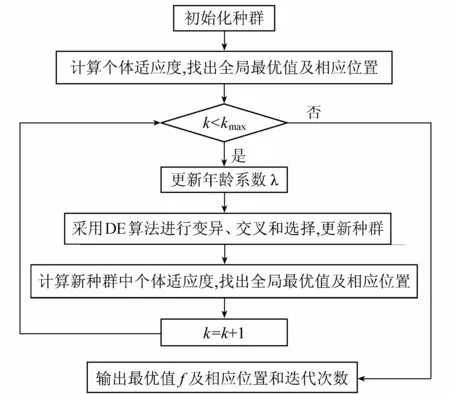
图1 DE算法优化的自步学习方法流程

3 数值试验

3.1 试验一

为验证本文方法的有效性,采用文献[2]的数据作为原始数据进行验证试验，试验中抽水流量为0.073 m3/s,持续时间为800 min。含水层类型、含水层介质、抽水试验的基本情况等水文地质条件详见文献[2]。表1为距抽水井30.48 m处观察孔中的水位降深观测数据。由于测量误差不可避免,给此原始数据添加较小的测量误差。考虑到实际情况,前50%数据添加服从N(0,1)分布的高斯误差,后50%添加服从N(0,10)分布的高斯误差。利用MATLAB语言编程进行数值试验。将采用DE算法的最小二乘法和本文方法进行对比,两种方法均采用相同参数(N=80,kmax=3 000,CR=0.8)进行求解,运行20次,所得参数T和μ均取20次结果的平均值。所得参数值代入式(3)中,模拟水位降深结果如图2所示。引入残差平方和RS对模拟结果进行评价:

(4)

式中:sRi为抽水开始后第i个时刻观察到的真实水位降深;sei为利用泰斯公式及其近似表达式[4]计算得到的第i个时刻水位降深。RS越小,说明模拟数据越接近原始数据。

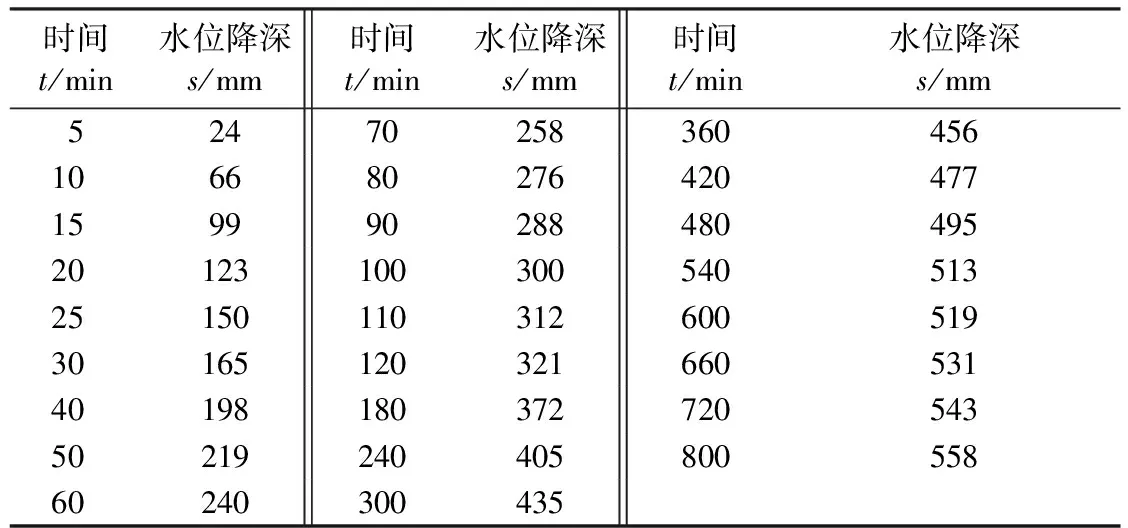
表1 水位降深观测数据

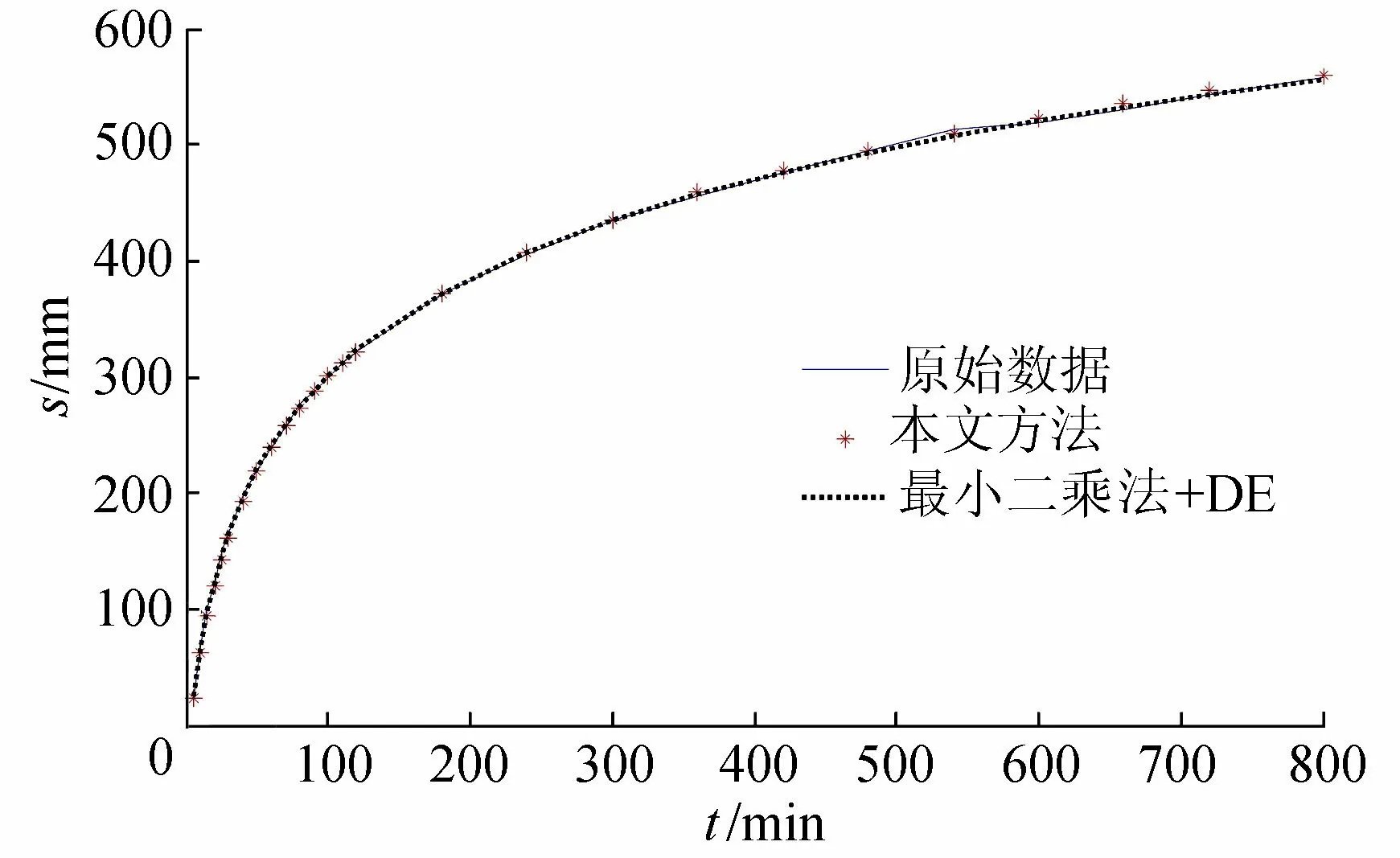
图2 试验结果对比(小误差)

在实测数据包含较小误差的情况下的试验结果对比如图2所示。由图2可知,本文方法与最小二乘法在相同的条件下,模拟数据与原始数据非常接近。将不同方法的计算结果列于表2。可以看出,两种方法所求参数值、残差平方和均相差不多。这表明,在误差较小的情况下,本文方法与最小二乘法均可以有效求解含水层参数。

3.2 试验二

考虑实际数据包含较大误差的情况,将原始数据前50%添加服从N(0,10)分布的高斯误差,后50%添加服从N(0,100)分布的高斯误差,然后随机选取约40%(10个)的数据作为缺失数据。在与试验一相同试验条件下,分别以最小二乘法和本文方法进行对比试验,所得模拟水位降深结果如图3所示。

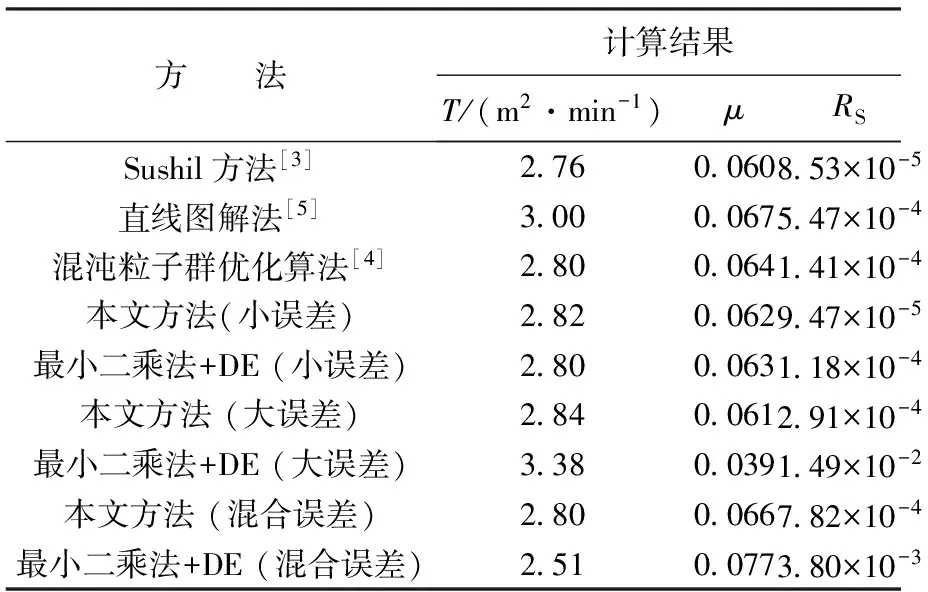
表2 不同方法计算结果

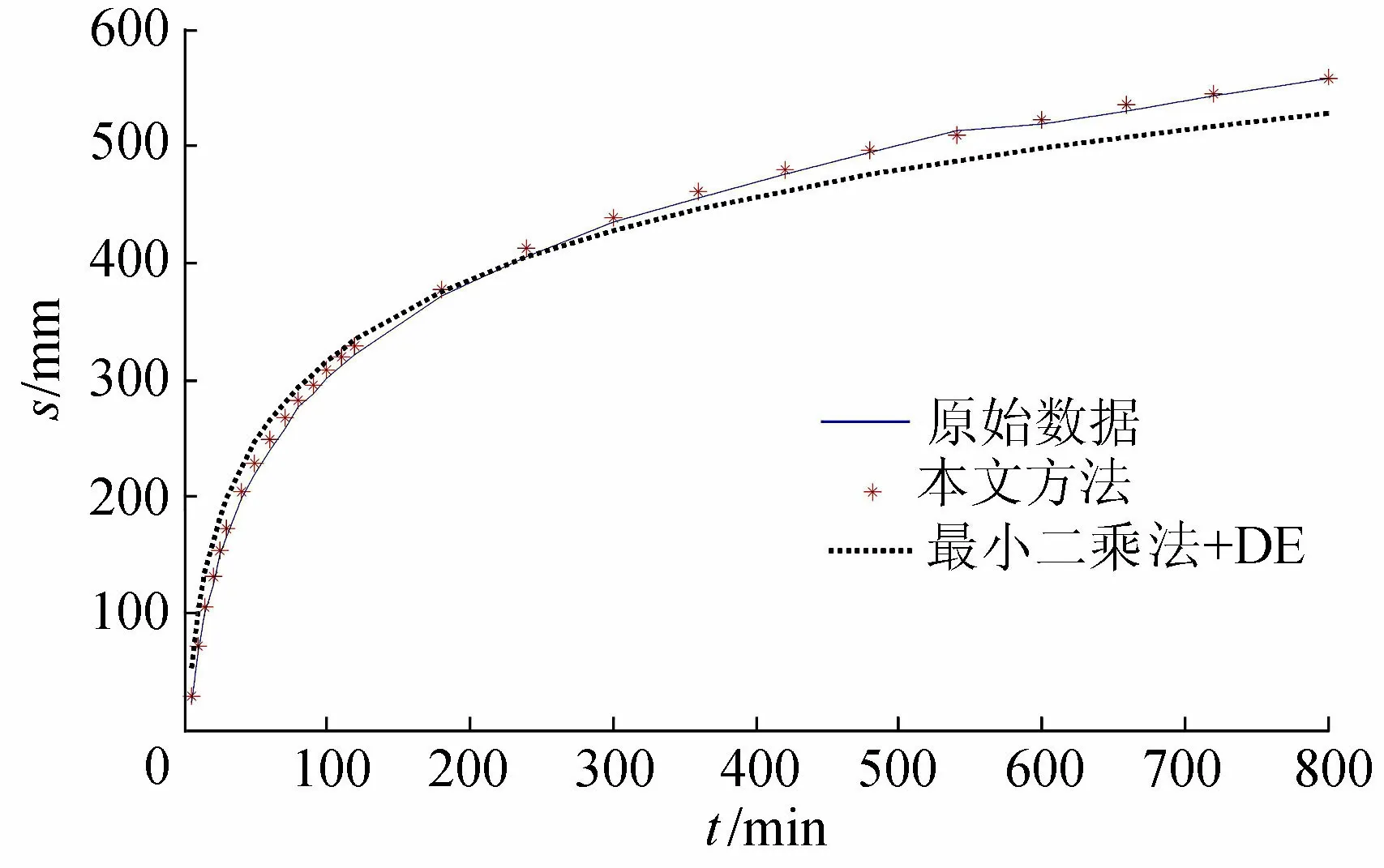
图3 试验结果对比(大误差)

由图3可以看出,当数据包含较大误差时,最小二乘法法计算结果严重偏离实际情况,而本文方法仍然可以较好地逼近原始数据。由表2可知,在参数值和残差平方和方面,本文方法均得到较好的结果。这表明,本文方法在数据误差较大时,可以有效地减小误差对计算结果的影响,保持较好的稳定性。

3.3 试验三

考虑到实际数据可能包含随机混合误差,将原始数据随机选取35%添加服从N(0,1)分布的高斯误差,随机选取35%添加服从N(0,10)分布的高斯误差,随机选取30%添加服从N(0,100)分布的高斯误差,然后随机选取约40%(10个)的数据作为缺失数据。在与试验一相同试验条件下,分别以最小二乘法和本文方法进行对比试验,所得模拟水位降深结果如图4所示。

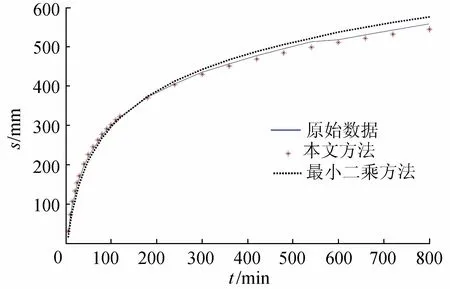
图4 试验结果对比(混合误差)

由图4可以看出,当测量数据包含随机混合误差时,最小二乘法方法计算结果和本文方法均有偏差,但本文方法更加逼近原始数据。表2中,本文方法所求参数值和残差平方和均接近传统方法并且优于最小二乘法。这表明,本文方法在实测数据包含混合随机误差时,可以有效地减少误差对计算结果的影响,保持较好的稳定性。

4 结 论

针对以往确定含水层参数的研究中没有考虑误差影响的情况,本文尝试将机器学习中自步学习方法引入到确定含水层参数中,构造了基于差分进化算法优化的自步学习方法,数值试验结果表明:①在误差较小的情况下,自步学习方法的精度与最小二乘方法相当的结果;②在误差较大的情况下,自步学习方法可以有效减少误差的影响,使得所求参数更加接近真实情况;③在实测数据包含随机混合误差情况下,此方法同样可以达到满意结果。因此,自步学习方法可以有效确定含水层参数,并保持良好稳定性。

[ 1 ] SUSHIL K S. Confined aquifer parameters from temporal derivative of drawdowns[J]. Journal of Hydraulic Engineering, 2001, 127 (6): 466-470.

[ 2 ] U. S. Department of the Interior (USDI). Groundwater Manual[M]. Washington,D. C.: U. S. Govment Printing Office,1977.

[ 3 ] 江思珉,蔡奕,王敏,等. 基于和声搜索算法的地下水污染源与未知含水层参数的同步反演研究[J].水利学报,2013,43 (12):1470-1477.(JIANG Simin, CAI Yi, WANG Min, et al. Simultaneous identification of groundwater contaminant source and aquifer parameters by harmony search algorithm[J]. Journal of Hydraulic Engineering, 2013,43(12):1470-1477.(in Chinese)).

[ 4 ] 周秀秀,常安定,郭建青,等.混沌粒子群优化算法在确定含水层参数中的应用[J].水资源与水工程学报,2013,24(1):96-99.(ZHOU Xiuxiu, CHANG Anding, GUO Jianqing, et al. Application of chaos particle swarm ptimization algorithms to estimation of aquifer parameters[J]. Journal of Water Resources & Water Engineering,2013,24(1):96-99. (in Chinese))

[ 5 ] BENGIO Y, LOURADOUR J, COLLOBERT R, et al. Curriculum learning[C]//International Conference on Machine Learning. New York:ACM, 2009:41-48.

[ 6 ] KUMAR M P, PACKER B, KOLLER D. Self-paced learning for latent variable models[C]//Proc of the Neural Information Processing Systems, New York:Curran Assciates, 2010:1189-1197.

[ 7 ] TANG K, RAMANATHAN V, LI F F, et al. Shifting weights: adapting object detectors from image to video[J]. Advances in Neural Information Processing Systems, 2012:638-646.

[ 8 ] KUMAR M P, TURKI H, DAN P, et al. Learning specific-class segmentation from diverse data[J]. Proceedings, 2011, 58(11):1800-1807.

[ 9 ] YONG J L, GRAUMAN K. Learning the easy things first: self-paced visual category discovery[C]//IEEE Conference on Computer Vision and Pattern Recognition. Piscataway:IEEE Computer Society, 2011:1721-1728.

[10] Supancic Iii J S, RAMANAN D. Self-paced learning for long-term tracking[J]Computer Vision & Pattern Recognition, 2013, 9(4):2379-2386

[11] ZHAO Q, MENG D, JIANG L, et al. Self-paced learning for matrix factorization[C]//Twenty-Ninth AAAI Conference on Artificial Intelligence. California:AAAI Press, 2015.

[12] JIANG L, MENG D, MITAMURA T, et al. Easy samples first: self-paced reranking for zero-example multimedia search[C]//ACM International Conference on Multimedia. New York:ACM,2014:547-556.

[13]王晓晨,常安定,王静云,等.各向异性含水层参数估计的差分进化算法[J]. 西北农林科技大学学报(自然科学版), 2015,43(4):223-228. (WANG Xiaochen, CHANG Anding, WANG Jingyun, et al. Differential evolution method for estimating the anisotropy aquifer parameters[J]. Journal of Northwest A&F University(Natural Science Edition), 2015,43(4):223-228.(in Chinese))

Applicationofself-pacedlearningtoestimationofaquiferparameters

YANG Chendong1, CHANG Anding2, ZHANG Ming1

(1.SchoolofScience,Xi’anAeronauticalUniversity,Xi’an710077,China; 2.SchoolofScience,Chang’anUniversity,Xi’an710061,China)

Through analysis of the pumping test data, which were affected by errors, an aquifer was investigated in order to present a new method for estimating the aquifer parameters. Based on the self-paced learning method in the machine learning field, a self-paced learning method based on the differential evolution algorithm was established and applied to the determination of aquifer parameters. This method was compared with other methods under errors of different levels. The numerical experimental results show that under errors of different levels, the differences between the values estimated with this method and traditional methods are small, and there are minor differences between the simulation data and original data. The results of the self-paced learning method, which was used for estimation of aquifer parameters based on pumping test data, are effective and reliable. The established algorithm is highly stable and it is seldom affected by data errors.

water resources; aquifer parameters; pumping test; self-paced learning; differential evolution algorithm

陕西省教育厅科研计划(16JK1394)

杨陈东(1990—),男,助教,硕士,主要从事最优化理论与方法研究。E-mail:yangchendong525@163.com

10.3880/j.issn.1006-7647.2017.05.013

TV211.1+2

：A

：1006-7647(2017)05-0074-04

2016-08-12 编辑：郑孝宇)