基于斐波那契迭代算法的贝叶斯软件可靠性验证测试方案

马振宇,， 吴 纬， 张 威， 刘福胜， 韩 坤

(1. 装甲兵工程学院技术保障工程系， 北京 100072； 2. 装甲兵工程学院信息工程系， 北京 100072；3. 北京特种车辆研究所， 北京 100072)

基于斐波那契迭代算法的贝叶斯软件可靠性验证测试方案

马振宇1,2， 吴 纬3， 张 威2， 刘福胜1， 韩 坤3

(1. 装甲兵工程学院技术保障工程系， 北京100072；2. 装甲兵工程学院信息工程系， 北京100072；3. 北京特种车辆研究所， 北京100072)

针对软件可靠性验证测试方案不能真实反映软件可靠性水平的问题，首先，根据贝叶斯原理构建了可靠性验证测试方案框架，并给出超参数的求解办法；然后，分析斐波那契排序规律，提出了斐波那契迭代算法；最后，提出了基于斐波那契迭代算法的贝叶斯软件可靠性验证测试方案，并对其进行实例验证。结果表明：斐波那契迭代算法能够真实地反映软件实际失效概率；在相同的置信度条件下，基于斐波那契迭代算法的贝叶斯软件可靠性验证测试方案能够明显减少测试所需的测试用例数。

斐波那契迭代算法； 贝叶斯方法； 可靠性验证测试； 软件可靠性

软件产品进行验收时，为检测软件的可靠性指标是否达标，必须要通过软件可靠性验证测试[1]。通常情况下，验证结果的置信度越高，软件的可靠性越好，但会大幅增加测试人员的工作量。特别是针对一些技术复杂、成本高和可靠性高的软件产品，验收时所产生的经济成本、人力成本和时间成本难以接受，导致软件可靠性验证测试难以进行。然而，使用贝叶斯方法(Bayesian method)可有效利用先验信息，在保证高置信度的条件下，能够显著减少可靠性验证测试的工作量。

目前，研究者针对贝叶斯软件的可靠性验证测试方法进行了大量工作。如：覃志东等[2-3]应用构造共轭分布的贝叶斯方法进行可靠性验证，利用先验信息为后验提供大量的实验信息，进而提出了基于先验动态整合的可靠性验证测试方法，该方法可很好地应用到实际工程中；王学成等[4]提出了基于减函数的先验分布构造法进行测试验证的方案，该方案在测试条件相同的情况下，可大幅缩短所需要的测试时长；刘广等[5]提出了基于减函数的多层贝叶斯软件可靠性验证测试方法，该方案通过双层贝叶斯方法进一步缩短了测试时长。

虽然前人[2-8]已进行了许多相关研究，但均在事先设定软件可靠性指标的前提下开展软件可靠性验证测试工作，这使得测试结果难以真实客观地反映软件实际的可靠性。尽管已有的二分(折半)查询法可解决该问题，但斐波那契迭代算法的查询平均性能更优。因此，笔者通过斐波那契迭代算法，预期得到软件的实际失效概率，并同时为软件的验证方法提供可靠性验证测试方案。

1 基于贝叶斯方法的可靠性验证测试方案

1.1基于贝叶斯方法的可靠性验证测试方案框架

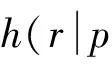
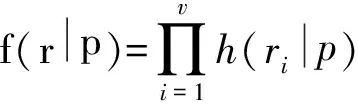
(1)

式中：p为被测软件的可靠性参数。本文设定p为失效概率。

假设p的先验分布函数为π(p)，则由失效概率和失效次数构成的联合分布函数为

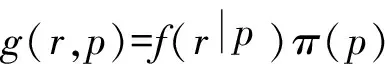
(2)

该函数将先验信息和样本信息有效地结合在一起。为了对p做出统计决策，引入条件分布(后验分布)

(3)

将联合分布函数进行变形，则有

(4)

式中：

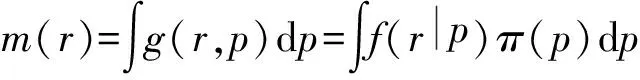
(5)

为边缘分布函数。

设定软件可靠性验证测试方案的指标为(p0，c，rm)，其中p0为规定的软件失效概率、c为置信度、rm为通过验证测试时的最大失效次数，则验证测试所需要的最小测试用例数nm为满足下列不等式的最小整数解，即有

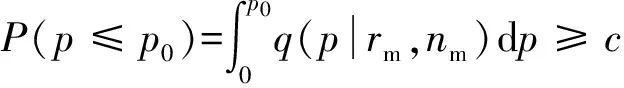
(6)

假设每次软件测试均符合n重伯努利实验[9-10]，那么在软件可靠性验证测试中，累计出现X次失效次数的概率符合二项分布，即

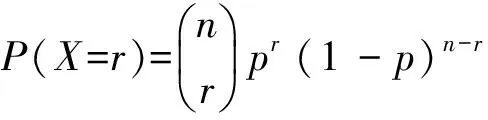
(7)

进一步推导出失效概率的先验分布为贝塔分布，即

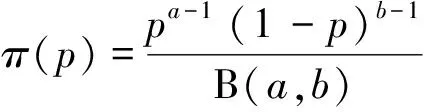
(8)

通常在结束软件测试后，会得到n′个测试用例，其中共有r′次失效，则失效概率的后验分布应为B(a+r′,b+n′-r′)，即

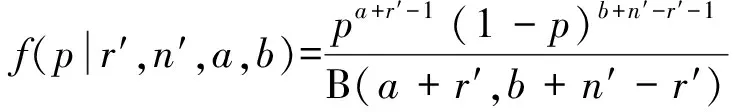
(9)

进行软件可靠性验证测试时，要求验证结果不能出现失效。在无失效的情况下，最少测试用例数应为满足下列不等式的最小整数解nm，即

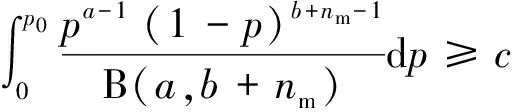
(10)

1.2超参数求解

根据超参数的求解原理[3]，可得超参数的具体估计过程为：首先，选用以往测试过程中遗留下的最后m组测试记录作为先验信息，每组含有l个测试用例；然后，统计每组测试用例中造成软件失效的数量，分别记作k1,k2,…,km；最后，求得失效概率的经验值tj=kj/l(j=1,2,…,m)。

结合式(5)、(7)、(8)，根据样本的边缘分布，可得

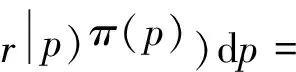
(11)

进而求得m(r)对应的一阶矩为

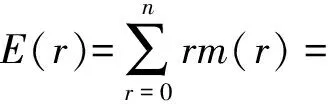
(12)

同理，可得h(r)的二阶矩，即

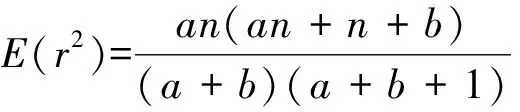
(13)

将E(r)、E(r2)记作w1、w2，则有

(14)

式中：D=(n-1)w12+n(w1-w2)。

w1、w2可通过经验样本值的期望估计得到，即

(15)

将式(15)代入式(14)中，即可估计出超参数a、b的值。

2 基于斐波那契迭代算法的贝叶斯验证方案

2.1斐波那契迭代算法

斐波那契(Fibonacci)算法是依据对有序表进行斐波那契查找[11]演变而来，而斐波那契查询法是在原有的二分(折半)查询法基础上改进而来，该方法在计算过程中只进行加减运算，不进行除法运算，因此斐波那契迭代算法查询平均性能要比二分查询法更优。

首先构造斐波那契序列，即

0,1,1,2,3,5,8,13,21,34,…。

(16)

由于任意一个有序序列的2个端点和中位点均与斐波那契数有联系。根据斐波那契排列规律提出如下定义：

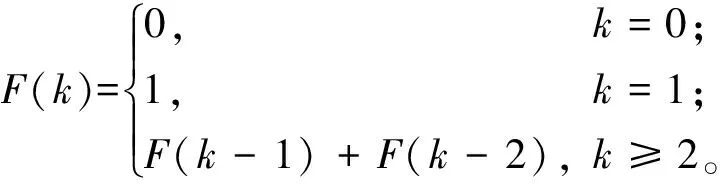
(17)

假设一个有序序列内共有m′个元素，且元素的个数等于某一个斐波那契数减去1，即m′=F(k)-1。若m′≠F(k)-1,则将该有序序列的最后1个元素重复填充到该序列，直到填充后序列中元素的个数与邻近的斐波那契数减1相等为止。

斐波那契迭代算法的基本原理为：对于一个序列中元素个数为F(k)-1的有序序列，令中位点为Fmid=Fmin+F(k-1)-1，(其中Fmin为该有序序列中最小元素的值)，得到分割以后的序列，其中左子序列中元素的个数为F(k-1)-1，右子序列中元素的个数为(F(k)-1)-(F(k-1)-1)-1=F(k-2)-1。由此可以看出：2个子序列中元素的个数依旧满足某一个斐波那契数减1，因此能够反复对该序列进行分割。具体过程如下：

1)对相关变量进行初始化。Fmin=a′;Fmax=F(k),为该有序序列中最大元素的值，其中F=F(k)-1为该有序序列的长度;b′=F(k-1)-1，为中位点的相对偏移量。

2)若Fmin>Fmax，则查询失败；否则，Fmid=Fmin+b′。

3)若F(k)Fmid，则F=F-b′-1,b′=b′-F-1,Fmin=Fmid+1，继续转入步骤2)；若F(k)=Fmid，则表示查寻成功，结束该迭代过程。

2.2算法实现

一般来说，基于贝叶斯方法的软件可靠性验证测试均提前对其失效概率进行了假设，通常未考虑软件本身实际的失效概率。为此，笔者在进行贝叶斯验证之前，通过斐波那契算法来确定被测软件的实际失效概率，这样既可使用软件实际的失效概率代替原来假设的失效概率，使软件可靠性验证测试过程更贴近实际；也可很好地利用先验贝叶斯的优势，在不降低试验结果置信度的前提下，有效减少所需测试用例数。

首先，对软件可靠性进行评估，可通过以往经验估计出该软件失效概率大致的取值范围，并设定两端的阈值；然后，通过斐波那契迭代算法找到实际失效概率的大致范围(误差不会超过1个数量级)；最后，确定软件的实际失效概率。图1为基于贝叶斯验证的斐波那契迭代算法实现步骤，具体过程如下：

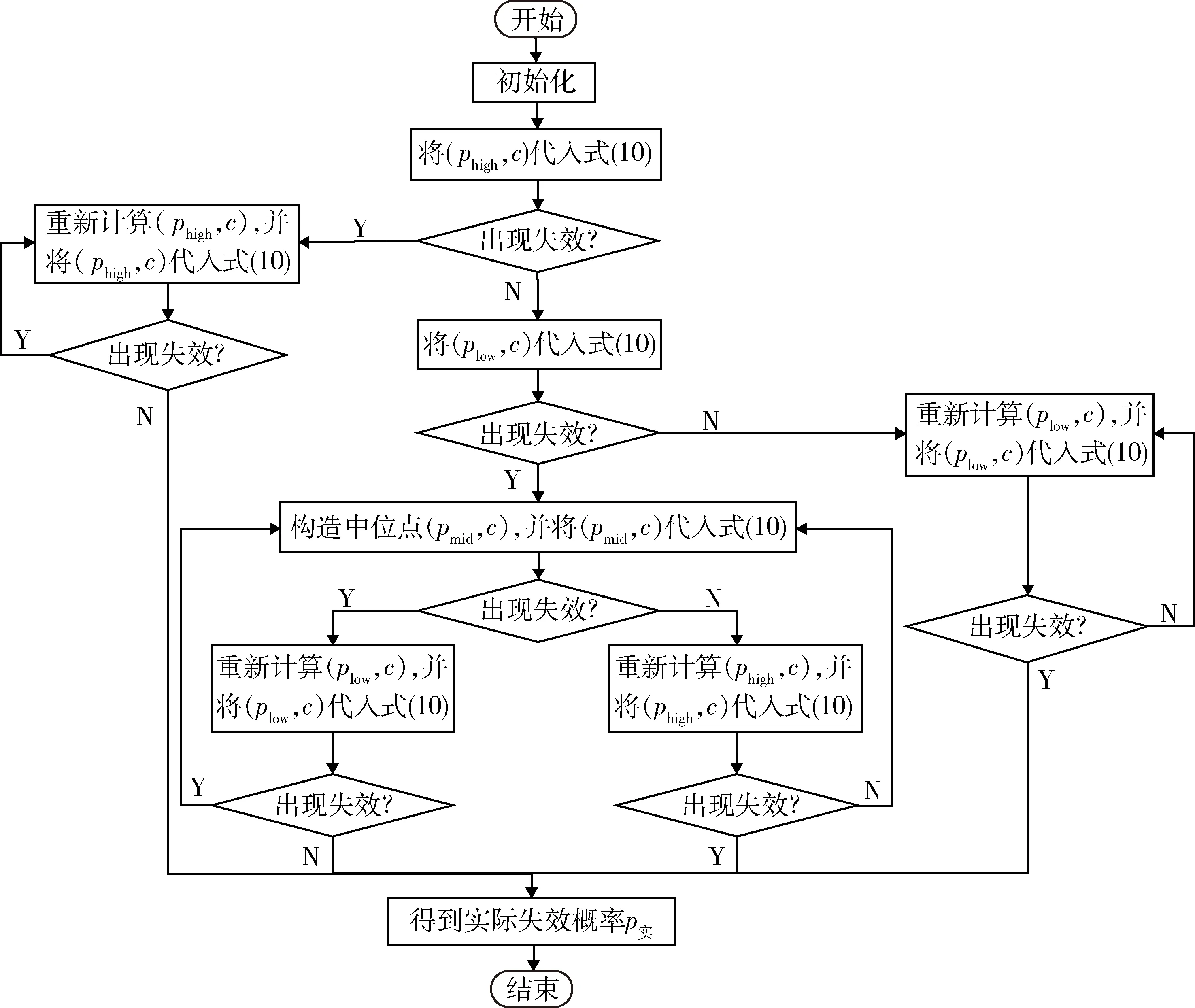
图1 基于斐波那契迭代算法的贝叶斯验证实现步骤

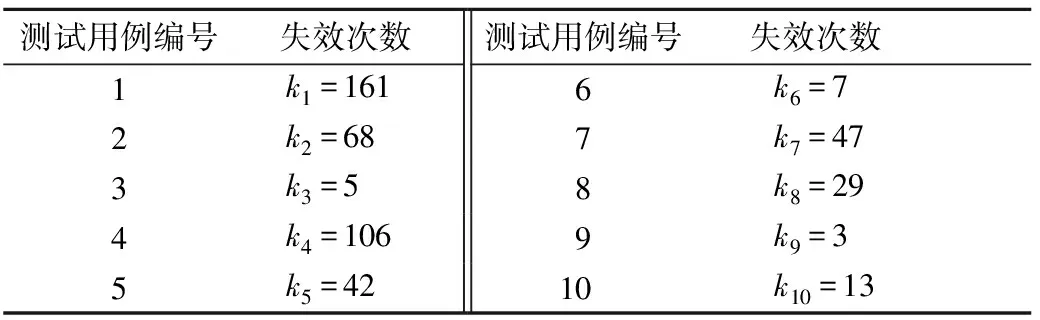
2)将(phigh,c)代入式(10)。若未出现失效，则p实

3)将(plow,c)代入式(10)。若未出现失效，则p实

4)令Fmid=Fmin+F(k-1)-1，将(pmid,c)代入式(10)。(1)若出现失效，则pmid≤p实

5)令Fmin=Fmin-1,phigh=10-Fmin，将(phigh,c)代入式(10)。若未出现失效，再将(0.1phigh-ε,c)、(0.1phigh+ε,c)分别代入式(10)，若结果分别是未失效、失效，则p实=0.1phigh，否则p实=phigh，此时迭代结束，求出最少测试用例数nm；若出现失效，则继续重复执行步骤5)。

6)令Fmax=Fmax+1,plow= 10-Fmax,将(plow,c)代入式(10)。若出现失效，再将(plow-ε,c)、(plow+ε,c)分别代入式(10)，若结果分别是未失效、失效，则p实=plow，否则p实=10plow，此时迭代结束，求出最少测试用例数nm；若未出现失效，则继续重复执行步骤6)。

3 实例验证

试验数据来自特种车辆软件测评中心对某项目进行实测得到的数据结果。首先，根据斐波那契迭代算法求解出实测软件的失效概率，假设Fmin=1,Fmax=12，构造一个差值为1的等差数列，那么phigh=10-1、plow=10-12，软件自身的失效概率计算结果如表1所示；然后，收集软件可靠性测试过程中最后10组数据作为先验信息的历史数据，每组测试用例数均为100000，每组出现的失效次数如表2所示；最后，依据本文提出的软件可靠性验证测试方案所得到的实验结果，验证该方法的有效性。

表1 基于斐波那契迭代算法的软件自身失效概率计算结果

表2 先验信息失效数据

由表1可知：在置信度为99%的条件下，实测软件的失效概率为0.001。根据表2中的历史信息，并结合式(12)-(15)，算出超参数a=1,b=2 067。

根据求得的软件本身实际的失效概率值以及超参数的估计值，设定软件可靠性验证测试方案的可靠性指标(p0，c，rm)=(0.001，0.99，0)，即置信度为99%，失效概率为0.001，最大允许失效次数为0。结合式(10)可得：在有先验信息的条件下，软件可靠性测试所需测试用例数为2 536，在无先验信息条件下所需测试用例数为4 602。这说明在保证置信度不变的条件下，所需测试用例数减少了2 066个，即可完成软件可靠性验证测试，论证了该方案的有效性。

4 结论

笔者基于斐波那契迭代算法求得被测软件的自身实际失效概率，且客观真实地反映出实测软件的实际可靠性。另外，在保证相同的置信度条件下，基于斐波那契迭代算法的贝叶斯软件可靠性验证测试方案能够显著降低可靠性验证测试所需测试用例数量。然而，对测试用例的选用如何做到完全随机性选择，还需要在以后的研究中进一步完善。

[1] 李海峰,刘畅,郑军.安全关键软件可靠性验证测试研究[J].航空标准化与质量,2013(3):46-50,58.

[2] 覃志东,雷航,桑楠,等.连续执行软件可靠性验证测试方法[J].计算机科学,2005,32(6):202-205.

[3] 覃志东,雷航,桑楠,等.安全关键软件可靠性验证测试方法研究[J].航空学报,2005,26(3):334-339.

[4] 王学成,陆民燕,李海峰,等.带减函数的连续型软件可靠性验证方案[J].重庆大学学报(自然科学版),2012,35(10):136-143.

[5] 刘广,黄百乔,刘畅,基于减函数的多层贝叶斯离散型软件可靠性验证测试方案[J].计算机应用研究,2017,33(3):761-764.

[6] 张文杰,杨华波,张士峰.基于Bayes混合验前分布的成败型产品可靠性评估[J].兵工学报,2016,37(3):505-511.

[7] 刘解放,刘思峰,方志耕.成败型产品可靠性评价的加权Bayes方法[J].中国机械工程,2013,24(24):3371-3374.

[8] 冯文哲,刘琦.成败型产品的Bayes可靠性验证试验设计[J].航空动力学报,2012,27(1):110-117.

[9] 刘海涛,张志华,董理.成败型产品可靠性的Bayes验收方案研究[J].兵工学报,2016,37(3):565-569.

[10] 刘琦,王囡,唐旻.成败型产品基于验后概率的Bayes序贯检验技术[J].航空动力学报,2013,28(3):494-500.

[11] 齐悦,夏克俭,姚琳.数据结构、算法与应用[M].北京：清华大学出版社,2015.

(责任编辑: 尚菲菲)

BayesianSoftwareReliabilityDemonstrationTestingSchemeBasedonFibonacciIterationAlgorithm

MA Zhen-Yu1,2, WU Wei3, ZHANG Wei2, LIU Fu-Sheng1, HAN Kun3

(1. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing100072, China；2. Department of Information Engineering, Academy of Armored Force Engineering, Beijing100072, China;3. Beijing Special Vehicle Research Institute, Beijing100072, China)

The software reliability demonstration testing cannot really reflect the software reliability level. To solve that problem, the framework of software reliability demonstration testing is constructed according to the Bayesian principle, and the solution of parameters is also given. Then the Fibonacci sort principle is analyzed, and Fibonacci iteration algorithms proposed. Finally, a Bayesian software demonstration testing scheme based on Fibonacci iterative algorithms put forward and verified. Examples show that the Fibonacci iterative algorithm can reflect the actual software failure probability, Bayesian software demonstration testing scheme based on Fibonacci iterative algorithm can obviously reduce the number of testing cases at the same confidence level.

Fibonacci iteration algorithm; Bayesian method; reliability demonstration testing; software reliability

1672-1497(2017)04-0116-05

2017-05-04

军队科研计划项目

马振宇(1991-)，男，博士研究生。

O213.2；TP311.5

：ADOI：10.3969/j.issn.1672-1497.2017.04.022