基于稀疏贝叶斯学习的电力线载波通信接收机设计

吕新荣，李有明，余明宸

（1. 宁波大学信息科学与工程学院，浙江 宁波 315211；2. 浙江工商职业技术学院，浙江 宁波 315012）

基于稀疏贝叶斯学习的电力线载波通信接收机设计

吕新荣1,2，李有明1，余明宸1

（1. 宁波大学信息科学与工程学院，浙江 宁波 315211；2. 浙江工商职业技术学院，浙江 宁波 315012）

针对多径信道和脉冲噪声对电力线载波通信系统性能影响的问题，提出了一种能有效对抗多径信道和脉冲噪声影响的电力线通信系统接收机设计方案。该方案将时域上的电力线信道参数和脉冲噪声联合视作稀疏向量，然后利用稀疏贝叶斯理论联合估计电力线信道和脉冲噪声，从而在接收端得以去除脉冲噪声及补偿信道增益。仿真结果表明，与传统将信道估计与脉冲噪声抑制单独考虑的传统接收机相比，本文提出的接收机方案在误符号率和误比特率等性能指标上有较好的提升。

电力线载波通信；信道估计；脉冲噪声；稀疏贝叶斯学习；正交频分复用

1 引言

新一代智能电网需要具有双向互动功能的通信基础设施作为保障。电力线通信（power line communication，PLC）技术借助于现有电力线网络传输数据信号，相较于其他通信技术，天然具有覆盖面最广及无需重新布线的优势。为了促进PLC技术的发展和应用，一些国际标准已经被推出，如PLC G3、PRIME、HomePlug和IEEE P1901等[1,2]。电力线通信的广泛应用还受到诸多限制，其中电力线信道的多径特性及信道中丰富的脉冲噪声是制约电力线通信系统性能的主要因素[3-5]。

正交频分复用（orthogonal frequency division multiplexing，OFDM）技术由于具有良好的对抗多径信道的能力，已经被各种PLC标准采纳作为物理层的传输技术[6]。完备的信道状态信息（channel state information，CSI）是保证OFDM接收机性能的关键，因此信道估计技术一直是研究的热点。现有的信道估计方法中绝大部分需要借助于导频或训练序列[7]。为了降低导频数量，提高频谱使用效率，基于压缩感知（compressed sensing，CS）理论的稀疏信道估计技术引起了广泛关注[8,9]。这类技术在无线通信技术领域获得了巨大成功，但由于电力线通信系统中存在丰富的脉冲噪声，这些信道估计技术的性能会极大降低。

即使可以获得完备的信道状态信息，脉冲噪声的出现也会导致OFDM接收机性能急剧恶化。为了消除脉冲噪声的影响，人们提出许多抑制脉冲噪声的方法，这些方法中比较典型的有限幅（clipping）、消隐（blanking）及基于压缩感知的方法。限幅或消隐法的原理基本相同，利用时域脉冲噪声的高幅值特点，将高于某个阈值的信号采样值判断为含有脉冲噪声，然后进行幅值限制或置零，这类方法性能的关键是阈值的确定[10]。由于脉冲噪声是突发的并且幅值远高于背景噪声，经过时域采样后具有明显的稀疏性，因此近几年开始研究利用压缩感知技术去估计接收信号中的脉冲噪声分量。参考文献[11]利用稀疏贝叶斯学习（sparse Bayesian learning，SBL）技术去抑制单输入单输出（single input single output，SISO）PLC系统中的脉冲噪声。参考文献[12]将该方法应用到多输入多输出（multiple input multiple output，MIMO）PLC系统中。这些方法都假设电力线信道状态信息在接收端是已知的，由于电力线信道是一种时变信道，要想在接收端获得准确的信道状态信息不是一件容易的事情。

在实际中，电力线信道的多径特性与脉冲噪声的影响是同时存在的，信道估计与脉冲噪声估计无法独立分开，因此联合估计信道和脉冲噪声逐渐引起重视。参考文献[13]利用因子图（factor graph）和消息传递方法联合估计信道和脉冲噪声，该设计方案假设信道服从瑞利分布并且信道的先验分布是已知的。由于电力线信道不服从瑞利分布[14]而且先验分布也无法得知，因此限制了该方法在实际电力线通信系统中的应用。参考文献[15]先用阈值方法去除脉冲噪声，然后利用DFT变换方法估计信道脉冲响应，这种方法需要预先知道信道的脉冲响应长度，并且假设信道在一个帧之内是不变的。参考文献[16]假设信道脉冲响应和脉冲噪声没有交迭，从而将信道脉冲响应和脉冲噪声之和视作一个稀疏向量，然后利用压缩感知技术估计信道脉冲响应和脉冲噪声。

本文通过分析基于OFDM的电力线通信系统特性，提出了一种联合信道估计、脉冲噪声抑制和数据符号检测的算法。该算法将电力线时域信道参数与脉冲噪声时域采样值联合视为一个稀疏向量，然后通过压缩感知理论去联合估计信道参数和脉冲噪声。为了提高估计性能，将发送的数据符号视为未知参数，在SBL[17]框架中利用期望值最大化（expectation maximization，EM）算法进行参数估计，从而在不增加导频数量的前提下，提高了算法的估计性能。

与传统方案相比，本文提出的方法的贡献主要有：无需获得电力线信道和脉冲噪声的正确先验分布信息，因而在实际电力线通信应用中具有更好的顽健性；能充分利用数据子载波的信息去提高估计性能，因而降低了导频需求，提高了频谱使用效率；仿真结果表明，本文提出的方法能在典型的电力线信道情况下较显著地提升PLC系统的误符号率和误比特率等性能指标。

2 系统模型

基于OFDM的PLC系统模型如图1所示，本文提出的信道估计与脉冲噪声联合估计模块位于 FFT模块之后，信道均衡模块之前，其他模块与传统PLC相同，这样可以尽量减少现有系统的改动。

信号源产生的二进制数据流b经过信道编码后映射为OFDM频域符号x=(x0,x1,…,xN-1)T，N为OFDM子载波数目。频域符号经过IDFT运算转换为 OFDM 时域符号，时域符号插入循环前缀（cyclic prefix，CP）后送入PLC信道。接收信号可以表示为：

其中，H是一个N×N循环矩阵，矩阵第一列是经过对信道脉冲响应向量 hL=(h0,h1,…,hL-1)T进行尾部零元素填充后构成，本文假设PLC的信道时延扩展长度为L；F表示离散傅里叶变化矩阵，F*是F的共轭转置；i表示脉冲噪声的时域采样值；g代表电力线信道的背景噪声，通常近似为加性高斯白噪声（AWGN），即

在接收端，首先去掉每个OFDM时域符号的循环前缀，然后经过FFT运算转变为OFDM频域符号y，该过程可以表示为：

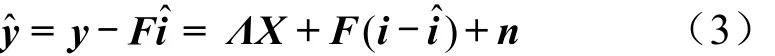
图1 基于OFDM的PLC系统模型

在文献中，电力线脉冲噪声通常使用Bernoulli-Gaussian（BG）、Gaussian-Mixture（GM）、Middleton Class A（MCA）3种模型描述。由于其他两种模型可以由GM模型表示，因此本文采用GM模型仿真脉冲噪声。在GM模型中，脉冲噪声采样值是若干个均值为0、方差不同的随机变量的总和。如用复数随机变量 z表示，相应的概率密度函数f(z)可以表示为：

其中，pk表示第 k个成分发生概率，满足是均值为0、方差为γk的复高斯分布。

3 基于SBL的联合估计算法

表示OFDM频域接收符号的式（2）可以重新表示为：

其中，X=diag(x)是对角矩阵，对角元素由OFDM子载波的数据符号组成。为了对抗电力线多径信道的时延扩展造成的符号间干扰，现在大多数PLC标准将OFDM符号的循环前缀（CP）长度设置为远大于信道时延扩展的长度，而 CP长度一般设置为OFDM符号长度的1/4，因此可以认为N≫L。经过填充（N-L）个零元素后的信道脉冲响应扩展为，可以认为是近似稀疏的。相应的式（5）可扩展为：

其中，矩阵Φ是一个欠定矩阵，同时注意到脉冲噪声变量i是稀疏的，进而联合构成的向量w可以视作稀疏的，因此式（7）形成了一个典型的压缩感知问题。在各种实际应用的压缩感知技术中，SBL技术因为独特优点受到了广泛关注，本文基于SBL技术提出了两种电力线信道与脉冲噪声联合估计算法。

3.1 非数据子载波的信道与脉冲噪声联合估计算法（JCI-SBL）

实际电力线通信系统中，由于电磁兼容的原因通常会将一部分子载波屏蔽，这部分子载波称为空子载波；在可用的子载波中，一部分子载波会发射导频符号用于信道估计，这部分子载波称为导频子载波；剩余子载波用于发射数据符号，称为数据子载波。将空子载波和导频子载波的索引集合记为，数据子载波索引集合记为D。当利用非数据子载波估计未知向量w时，式（7）中对应非数据子载波部分为：

在SBL中，假设未知向量w的先验概率服从独立高斯分布：

则w的后验概率仍旧服从高斯分布：

其中，均值μ和协方差矩阵Σ分别为：

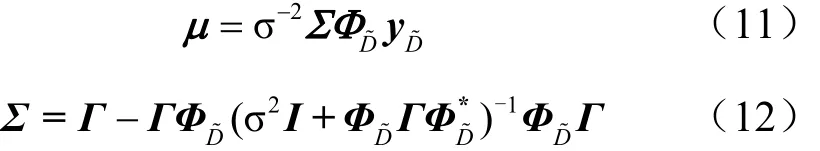
SBL将均值μ作为w的MAP（最大后验概率）估计。由于在式（11）和式（12）含有未知超参数Г和σ2，因此均值μ和协方差矩阵Σ无法直接计算。为了估计这些超参数，通常使用Type-Ⅱ最大似然估计方法，该方法通过最大化接收信号y的边缘概率求解超参数。由于这种方法无法直接获得超参数的闭式解，需要利用EM算法迭代逼近最优解。

利用EM算法求解超参数Г和σ2的步骤分为E步骤和M步骤。

· E步骤：将未知向量w视作隐含变量，计

· M步骤：利用先固定一个参数再求解另外一个参数的方式，交替求解最优超参数Г(k+1)和(σ2)(k+1)，其中k表示迭代的次数：

Г(k+1)和(σ2)(k+1)的解分别为：

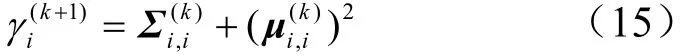
其中，N表示非数据子载波的数目。求得Г(k+1)和(σ2)(k+1)后将结果代入式（11）和式（12），计算后验概率分布p (w| y)的均值μ和协方差矩阵Σ，然后将新的μ和Σ值代入式（15）和式（16）重新估计超参数值。上述步骤交替执行，当达到算法的收敛条件后，算法终止。这时最终的均值μ即w的MAP估计值。根据w的定义，电力线信道的估计为=[1:N]，脉冲噪声的估计为

3.2 同步数据符号检测的信道和脉冲噪声联合估计算法（JCIS-SBL）

JCI-SBL算法的性能受到非数据子载波数目的限制，然而增加非数据子载波的数目则会减少系统的数据子载波数量，进而降低系统通信容量。如果能使用OFDM符号中的所有子载波联合估计信道和脉冲噪声，那么就可以期望在不降低系统通信容量的情况下提高算法的估计性能。

当使用全部子载波后，系统模型如式（7）所示，因此w的后验概率的均值μ和协方差矩阵Σ分别为：

其中，c是与X无关的量，Tr(.)表示求矩阵的迹。结合Φ、μ、Σ的定义可得：

在实际中，信道与脉冲噪声可以认为是互相独立且不相关的，为了防止过拟合，将式（22）中的Σih和Σhi强制为零矩阵，将式（22）代入式（21），利用X和矩阵迹的性质，可得：

其中，j∈D，Ω表示发射信号星座点组成的集合，F(j,:)表示矩阵F的第j行。上述推导过程为了简化书写已将表示迭代过程的上标省略。

JCIS-SBL的初始化需要提供X的初始值，如果随机选择星座点作为 X的元素，会导致算法不收敛，因此可以先采用仅需要非数据子载波的 JCI-SBL估计出信道和脉冲噪声，然后经过均衡和判决后得到X的估计值X(0)，将这个估计值和JCI-SBL的输出一同作为JCIS-SBL的初始值输入。

4 仿真结果与分析

为了验证算法的性能，利用MATLAB进行仿真。电力线的信道频域响应采用广泛应用的多径信道模型[14]：

其中，A、K2、K、α0、α1、v和 Np都是常数；gi、ci、ℓi都是随机变量。本文仿真参数设置如下：Np=10，最大路径长度为800 m，每条路径长度服从[0,800]区间的均匀分布，频带范围为[35,91] kHz。按照式（24）生成信道频域响应H(f)后，对H(f)进行IDFT运算得到复数信道时域响应 h(t)，本文假设信道的最大时延扩展长度L=32，因此需要对h(t)截断取前32位。

OFDM的仿真参数设置为：总载波数为256，其中循环前缀的长度为64，导频子载波数分别为32（即循环前缀长度的一半）和64（即循环前缀的长度），空子载波数为100，数据子载波数为124。信号调制模式采用4QAM。脉冲噪声采用GM 模型，其中

在仿真结果中，“JCI”和“JCIS”分别代表本文提出的 JCI-SBL、JCIS-SBL两种算法。“MMSE”代表在已知准确的信道参数和脉冲噪声的统计信息下利用LMMSE算法估计时域脉冲噪声，代表线性估计中的最优估计性能；“DFT”代表接收机已知信道准确信息下但未抑制脉冲噪声时的系统性能；“LS”代表先利用空子载波抑制脉冲噪声后再基于导频符号利用最小二乘法估计信道参数时系统性能，代表脉冲噪声抑制和信道估计独立进行时系统性能；“FG”代表参考文献[13]提出的基于因子图的联合估计方法性能。

现在主流的电力线通信系统标准既支持信道编码也支持不使用信道编码，因此本文首先对各种方法的误符号率（symbol error rate，SER）性能进行对比，图2给出导频数为32和64时不同方法的SER和SNR的曲线变化情况。

图2 不同方法的SER和SNR的曲线变化情况

从图2可以看出，本文提出的JCI和JCIS算法表现出了良好性能。使用JCIS和JCI算法的系统性能要比未抑制脉冲噪声的系统性能显著提高15 dB。由于JCIS利用了所有子载波信息，因此比仅利用非数据子载波信息的JCI性能有明显提高。同时JCIS性能与MMSE算法的性能基本一致。此外还可以看出，LS算法的性能比DFT算法的性能要差，而DFT算法比JCI和JCIS算法性能差，这说明在准确信道状态信息已知的情况下，OFDM具有一定的对抗脉冲噪声性能，但是如果能够去除脉冲噪声的影响，系统性能可以得到显著提高，同时还表明脉冲噪声抑制的效果会显著影响信道估计的性能。由于 JCI和 JCIS利用非零子载波来联合估计信道和脉冲噪声，因此与传统独立进行脉冲噪声抑制和信道估计的方案相比，性能有显著提高。由于FG算法需要知道电力线信道和脉冲噪声的先验分布信息，本文采用GM分布作为电力线信道和脉冲噪声的先验分布，由于先验分布与实际分布的不匹配，因此 FG算法的性能很差。

图2(b)和图2(a)相比，增加导频数目有助于提高系统性能，但是增加导频数目会降低系统的频谱利用率，因此在实际中需要根据实际情况进行平衡。

卷积码是现代许多电力线通信系统采用的信道编码技术。因此本文也在基于卷积码的系统上进行了误比特率（bit error rate，BER）性能测试。图3给出基于卷积码系统的导频数为32和64时不同方法的BER和SNR的曲线变化情况。

从图3可以看出，在导频数为32时本文提出的JCIS和JCI算法的系统性能要比DFT和LS方法的性能显著提高15 dB，当导频数为64时，性能要提高近20 dB。这表明与传统独立进行脉冲噪声抑制和信道估计的方案相比，本文提出的联合估计信道和脉冲噪声的新型接收机的性能有显著提升。通过图3的对比可以看出，随着导频数的增加，JCI的性能有明显提升。当导频数为64时，JCI的性能与JCIS的性能比较接近，这是因为信道编码具有纠错功能，可以提升系统对信道和脉冲噪声估计的误差的顽健性。选择更优秀的信道编码技术可以提高PLC系统的性能和顽健性，但需要考虑信道编码实现的复杂性。

图3 不同方法的BER和SNR的曲线变化情况

5 结束语

本文基于稀疏贝叶斯技术设计了一种能联合估计信道、脉冲噪声和数据符号的SISO-PLC接收机。与传统将脉冲噪声抑制和信道估计分开进行单独考虑的思路相比，本文将脉冲噪声抑制和信道估计同步进行。利用信道和脉冲噪声的稀疏性，构建了一个利用压缩感知模型去联合估计电力线信道和脉冲噪声的估计方法。仿真结果表明，该接收机具有较好的性能。特别在低信噪比情况下，本文提出的算法相比其他算法具有显著的性能提升。

[1] CANO C, PITTOLO A, MALONE D, et al. State of the art inpower line communications: from the applications to the medium[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(7): 1935-1952.

[2] BERGER L T, SCHWAGER A, PAGANI P, et al. MIMO power line communications[J]. IEEE Communications Surveys & Tutorials, 2014, 17(1): 106-124.

[3] CORCHADO J A, CORTÉS J A, CAÑETE F J, et al. An MTL-based channel model for indoor broadband MIMO power line communications[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(7): 2045-2055.

[4] ZIMMERMANN M, DOSTERT K. A multipath model for the powerline channel[J]. IEEE Transactions on Communications, 2002, 50(4): 553-559.

[5] ZIMMERMANN M, DOSTERT K. Analysis and modeling of impulse noise in broadband powerline communications[J]. IEEE Transactions on Electromagnetic Compatibility, 2002, 44(1): 249-258.

[6] 杨昉, 何丽峰, 潘长勇. OFDM原理与标准-通信技术的演进[M].北京: 电子工业出版社, 2013. YANG F, HE L F, PAN C Y. OFDM principles and standards: evolution of communications techniques[M]. Beijing: Publishing House of Electronics Industry, 2013.

[7] LIU Y, TAN Z, HU H, et al. Channel estimation for OFDM[J]. IEEE Communications Surveys & Tutorials, 2014, 16(4): 1891-1908.

[8] PRASAD R, MURTHY C R, RAO B D. Joint approximately sparse channel estimation and data detection in OFDM systems using sparse bayesian learning[J]. IEEE Transactions on Signal Processing, 2014, 62(14): 3591-3603.

[9] DING W, LU Y, YANG F, et al. Spectrally efficient CSI acquisition for power line communications: a bayesian compressive sensing perspective[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(7): 2022-2032.

[10] ZHIDKOV S V. Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers[J]. IEEE Transactions on Communications, 2008, 56(1): 5-9.

[11] LIN J, NASSAR M, EVANS B L. Impulsive noise mitigation in powerline communications using sparse Bayesian learning[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(7): 1172-1183.

[12] 呙涛, 胡国荣. 基于稀疏贝叶斯学习的MIMO电力线脉冲噪声消除[J]. 电力系统自动化, 2014, 38(14): 95-100. GUO T, HU G R. Impulsive noise mitigation on MIMO power line based sparse Bayesian learning[J]. Automation of Electric Power System, 2014, 38(14): 95-100.

[13] NASSAR M, SCHNITER P, EVANS B L. A factor graph approach to joint OFDM channel estimation and decoding in impulsive noise environments[J]. IEEE Transactions on Signal Processing, 2014, 62(6): 1576-1589.

[14] TONELLO A M, VERSOLATTO F, BÉJAR B, et al. A fitting algorithm for random modeling the PLC channel[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1477-1484.

[15] CHIEN Y R. Iterative channel estimation and impulsive noise mitigation algorithm for OFDM-based receivers with application to power-line communications[J]. IEEE Transactions on Power Delivery, 2015, 30(6): 2435-2442.

[16] MEHBOOB A, LI Z, KHANGOSSTAR J, et al. Joint channel and impulsive noise estimation for OFDM based power line communication systems using compressed sensing[C]//IEEE International Symposium on Power Line Communications and its Applications, March 24-27, 2013, Johannesburg, South Africa. New Jersey: IEEE Press, 2013: 203-208.

[17] WIPF D P, RAO B D. Sparse bayesian learning for basis selection[J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153-2164.

Design of transceivers based on sparse Bayesian learning for power line carrier communications

LV Xinrong1,2, LI Youming1, YU Mingchen1
1. College of Information Science and Engineering, Ningbo University, Ningbo 315211, China 2. Zhejiang Business & Technology Institute, Ningbo 315012, China

Aiming at the problem of the influence of multipath channel and impulse noise on the performance of power line carrier communication system, a transceiver scheme for power line communication system was proposed which could effectively combat the influence of multipath channel and impulse noise. Firstly, the power line channel impulse response and the impulsive noise in the time domain were jointly viewed as a sparse vector. Then, the sparse Bayesian learning theory was adopted to estimate the power line channel and impulse noise jointly. The impulse noise was removed and the channel gain was compensated at the receiver. The simulation result shows that the proposed receiver scheme has better performance than traditional receiver considering channel estimation and impulse noise suppression separately.

power line carrier communication, channel estimation, impulsive noise, sparse Bayesian learning, orthogonal frequency division multiplexing

s: The National Natural Science Foundation of China (No.61571250), Ningbo Natural Science Foundation of China (No.2015A610121)

TN913

：A

10.11959/j.issn.1000-0801.2017196

吕新荣（1976-），男，宁波大学信息科学与工程学院博士生，主要研究方向为电力线通信、稀疏信号处理、压缩感知。

李有明（1963-），男，宁波大学信息科学与工程学院教授、博士生导师，主要研究方向为宽带通信、电力线通信、协作中继、认知无线电等。

余明宸（1991-），男，宁波大学信息科学与工程学院硕士生，主要研究方向为电力线通信系统脉冲干扰。

2017-03-20；

：2017-06-07

李有明，liyouming@nbu.edu.cn

国家自然科学基金资助项目（No.61571250）；宁波市自然科学基金资助项目（No.2015A610121）