Application of binding theory for seepage of viscoelastic fluid in a variable diameter capillary*
Er-long Yang (杨二龙), Ting-ting Gu (谷婷婷), Mei Wang (王梅), Huan Li (李欢)
1.Key Laboratory on Enhanced Oil and Gas Recovery of the Ministry of Education, Northeast Petroleum University, Daqing 163318, China, E-mail: yel13796988396@126.com
2.Daqing Oilfield of China National Petroleum Corporation, Daqing 163000, China
3.School of Computer and Information Technology, Northeast Petroleum University, Daqing 163318, China
4.Second Oil Production Plant of Daqing Oilfield of CNPC, Daqing 163511, China
Application of binding theory for seepage of viscoelastic fluid in a variable diameter capillary*
Er-long Yang (杨二龙)1, Ting-ting Gu (谷婷婷)2, Mei Wang (王梅)3, Huan Li (李欢)4
1.Key Laboratory on Enhanced Oil and Gas Recovery of the Ministry of Education, Northeast Petroleum University, Daqing 163318, China, E-mail: yel13796988396@126.com
2.Daqing Oilfield of China National Petroleum Corporation, Daqing 163000, China
3.School of Computer and Information Technology, Northeast Petroleum University, Daqing 163318, China
4.Second Oil Production Plant of Daqing Oilfield of CNPC, Daqing 163511, China
The polymer solution for polymer flooding is a viscoelastic fluid. There exist both shear flow and elongational flow when the polymer solution flows in a porous medium, where an additional dissipation is involved. The additional dissipation caused by elongational deformation is often ignored while studying the flow of the fluid in a porous medium. For a complex polymer solution, the generated elongational pressure drop cannot be ignored. In a capillary of fixed diameter, the polymer solution is only impacted by the shear force, and its rheological property is pseudoplastic. Therefore the variable diameter capillary and the converging-diverging flow model with different cross sections are required to describe the flow characteristics of the polymer solution in porous media more accurately. When the polymer solution flows through the port, we have the elongational flow and the polymer molecules undergo elongational deformation elastically. By using the mechanical energy balance principle and the minimum energy principle, a mathematical model of non-Newtonian fluid inlet flow was established by Binding. On the basis of the Binding theory, with the application of the theory of viscoelastic fluid flow in the circular capillary and the contraction - expansion tube, the relations between the viscoelastic fluid flow rate and the pressure drop are obtained.
Binding theory, viscoelastic fluid, abrupt contraction capillary, permeability rule
Introduction
To accurately describe the constitutive equations of the viscoelastic fluid is the key in this study. In particular, the indoor measurement for the characterization of the elongational viscosity is quite difficult[1,2]. That is why Liang Jizhao applied correction factors as done by Bagley to eliminate the elongational viscosity in his study[3]. Wever et al.[4]presented experimental results of shearing and stretching flows and the first normal-stress difference of the PAM in detail,together with the seepage rule of the polymer solution in four ideal porous media.
When the polymer solution flows in porous media, there exist both the elongational flow and the shear flow during the oil displacement. The additional dissipation due to the elongational deformation is often ignored in the studies of the fluid flow in porous media. For the laminar flow of the Newtonian fluid, this result is supported by experiment. But for the polymer solution the situation is more complex, the elongational pressure drop of the fluid flow through porous media can not to be ignored.
In the capillary of a fixed diameter, the polymer solution is only affected by the shear force, and its rheological property is pseudoplastic. Therefore the variable diameter capillary and the converging-expansion flow model of different cross section shapes are used to describe the flow characteristics of the polymer solution in porous media more accurately. When flowing through these flow channels, the polymersolution generates an elongational flow, and the polymer molecules have elongational deformations elastically[5-8]. Under the condition that the elongational viscosity is assumed as a constant, Sienz et al.[9]gave an analytical solution of the pressure drop in the contracting channel by using the cylindrical coordinates and the infinitesimal force balance method[10].
With the principles of the mechanical energy balance and the minimum energy, Binding established a mathematical model of the non-Newtonian fluid inlet flow convergence[11].Although the original intention of the method is to analyze the extension viscosity of the eupolymer, this method can be used to calculate the relationship between the pressure drop and the flow rate in variable diameter capillaries, under the condition that the elongational and rheological properties of the polymer solution are known and the flow in porous media meets the assumption of macroscopic continuum mechanics.

Fig.1 Schematic diagram of abrupt contraction capillary
1. Work of binding
1.1 Model building
As shown in Fig.1, the abrupt contraction capillary is a kind of representative porosity models. The capillary length isL, the entrance radius isR0, the exit radius isR1, and the ratio of the pore throats is. When a non-Newtonian fluid flows from a large cross section channel into a small cross section channel, because of the abrupt contraction of the channel’s cross section, the fluid flow line is not parallel and forms a cone boundary. The fluid’s natural convergence half angle between the tangent to the boundary line and the center line of the passage is not all equal to the entrance half angle of the passage. When the current angle is less than the latter, before the entrance of the flow channel area, a so-called“circulation area” will be formed, in which the fluid will be in a vortex motion[12]. The circulation of the fluid movement is prone to induce unstable flow phenomenon, and lead to additional energy consumption, a serious concern.
1.2 Method development
Assume that the boundary flow line of the convergent flow in the entry of the capillary tube shown in Fig.1 is a curved cone, and is in an axial symmetry. The busbar of the cone can be represented as:R=f(z).When the cylindrical coordinates are used, the velocity field can be expressed as:

The strain rate components are:

In Eq.(6), (dR/dz)2and d2R/d2zare ignored, and the following conditions are satisfied: whenZ=0,R=R1, if the shear viscosity and the elongational viscosity of the polymer solution obey the power law relationship, according to the principle of the minimum energy, the boundary flow line can be decribed as
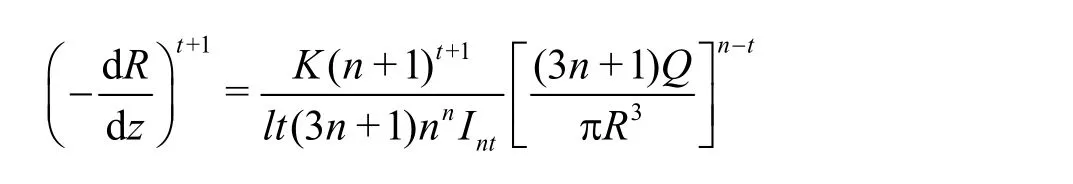
With the introduction of the Binding’s approximate method, the length of the spiralLvis given as follows


Table 1 Rheology parameters for various concentration PAM

In Eq.(7),is the tube wall shear rate at the exit of the capillary. The pressure drop of the whole capillary is
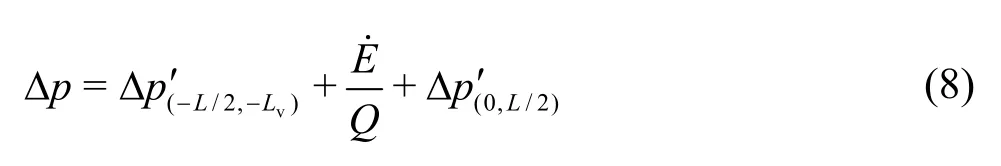
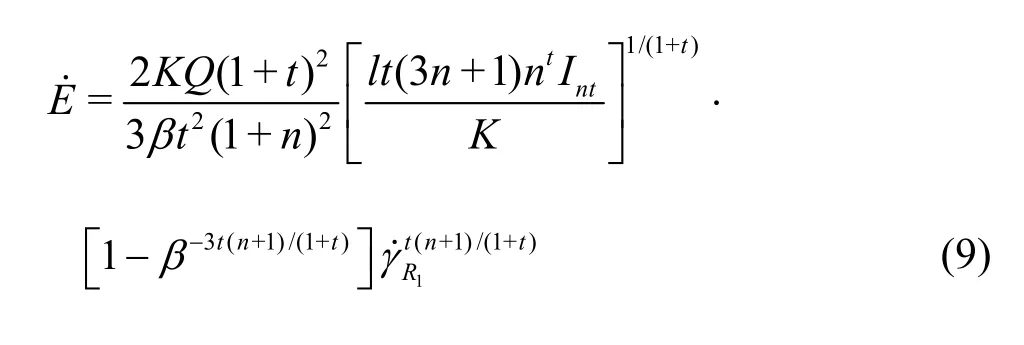
Given the geometric parameters of the capillary model and the rheological parameter of the fluid, the pressure drop of the abrupt contraction capillary can be calculated by Eq.(8).
2. The influence of pore throat ratio and throat radius on pressure drop of converging capillary
To study the effects of the pore throat ratio on the pressure drop of a converging capillary, the polymer solution with a concentration of 1 000 mg/L is used as an example. The rheological parameters are shown in Table 1. The length of the capillary modelL=100μ m, the entry radiusR0=40μm, the flow quantityQ=5× 10-14m3/s. Figure 2 shows the pressure drop gradient of the polymer solution in different converging capillaries with the pore throat ratioβ. In Fig.2,Ais entrance pressure drop gradient andBis average pressure drop gradient.
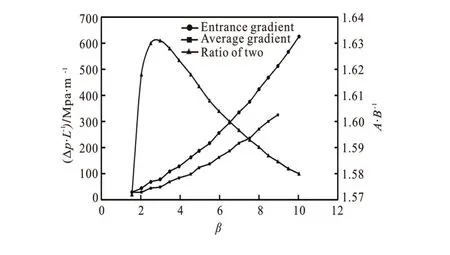
Fig.2 Pressure drop gradients as a function ofβ
Figure 2 shows that the entrance pressure drop gradient and the average pressure drop gradient both increase with the increase of the pore throat ratio. The larger the pore throat ratio, the greater the pressure drop gradient. This is because the larger the pore throat ratio, the greater the stretching effect and the resulting additional pressure gradient. Besides the enhanced stretch, with the increase of the pore throat ratio, the downstream export radius is reduced, which increases the pressure drop gradient of the laminar flow period, and which is another reason for the increase of the average pressure gradient. The ratio of the entrance pressure drop gradient to the average pre-ssure drop gradient is only related to the pore throat ratio, and the ratio first increases later drops along with the increase of the pore throat ratio. In the case of a low pore throat ratio, with the increase of the pore throat ratio, the stretching of the polymer solution increases, therefore the additional pressure gradient increases quickly. The growth rate beyond that of the laminar flow pressure drop gradient caused by the decrease of the downstream export radius increases the ratio of the entrance pressure drop gradient to the average pressure drop gradient as the pore throat ratio increases. With the further increase of the pore throat ratio, although the elongational flow is stronger, the pressure drop gradient increases faster due to the sharp decrease of the downstream radius. Therefore, the ratio of the entrance pressure drop gradient to the average pressure drop gradient decreases with the increase of the pore throat ratio. However, when the exit radius is a constant value, the results are the opposite, namely, the ratio of the entrance pressure drop gradient to the average pressure drop gradient decreases along with the increase of the pore throat ratio. The reason is that while the pore throat ratio increases, the average radius increases, with the same flow rate, the pressure drop gradient will surely decrease. And under the condition of a fixed entrance radius, while the pore throat ratio increases, the average radius decreases, with the same flow rate, the pressure drop gradient will increase.
Take the polymer solution of a concentration of 1 000 mg/L as an example. The length of the capillary modelL=100μ m , the pore throat ratioβ=4, the flow quantityQ=5× 10-14m3/s . As shown in Fig.3, the throat radius has a significant effect on the pressure drop gradient.

Fig.3 Pressure drop gradients as a function of throat radius (r)
With the increase of the throat radius, the entrance pressure drop gradient and the average gradient are both reduced rapidly. Therefore, the smaller the throat, the larger the additional pressure gradient caused by the elongational properties of the polymer solution, namely, the larger the percolating resistance.
3. The application of binding’s theory
The analysis of the Binding’s method shows that the pressure drop in the whole capillary is proportional to the flow rate. That means that using the minimum energy principle to determine the length of the vortex, the result will not be accurate, and cannot accurately predict the phenomenon that the resistance increases while the velocity of the viscoelastic fluid is greater than the critical one. In the study of the rheology and the flow of the polymer solution in porous media, except for the abrupt contraction capillary and abrupt enlargement capillary models, the gradual contraction capillary and gradual enlargement capillary models, as well as the pore models are constantly used. The characteristics of these pipes are as follows. The pore radius changes slowly along thezaxis, the flow of the fluid in the pipe contains both the radial flow and the axial flow, but the radial flow can be consi- dered as with a symmetry[13]. In this case, the wall velocity is assumed as zero, and there are no secon- dary flow and vortex. As the fluid boundary is known, the energy dissipation in the whole capillary can be directly calculated without applying the principle of the minimum energy. The calculation results show that the improved method can reflect the seepage characteristics of the viscoelastic fluid.
The pressure drop of the whole capillary can be obtained by integration

Equation (10) is replaced as[14]
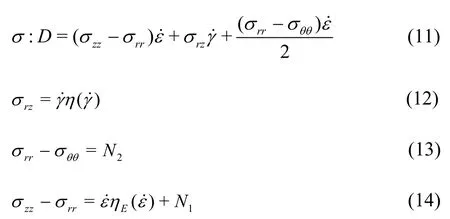
Substituting Eqs.(12)-(14) into Eq.(11), and in view of the fact that, we obtain the following equation

For the polymer solution,N2is much smaller thanN1, andis also much smaller thanso, in Eq.(15), the related terms can be ignored.
When the constitutive equation of the viscoela-stic polymer solution can be described by, Eq(15) can be replaced by

By Eq.(16), the following equations can be obtained:
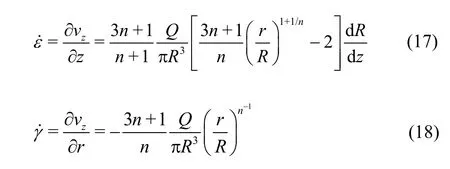
Substituting Eq.(16) into Eq.(10), the right hand side of the equation becomes

With the integration of the equation over the whole capillary volume or the volume between the entrance and exit cross sections, we obtain Eqs.(20), (21) and (22). The three equations are, respectively, with respect to the shear pressure drop Δps, the elastic pressure drop caused by the first normal stress difference Δpelaand the elongational pressure drop Δpe.R0andRL, respectively, represent the cross section radii of the inlet side and the outlet side of the capillary.


Equation (20) shows that, it is an elastic relation, namely, the pressure drop caused by the first normal stress difference is only related to the section radii of the inlet side and the outlet side, and has no relation to the change of the capillary onZaxis.

In Eq.(21)is a function of the power-law indexnand the elongational indext, which can be obtained by the function quad8 in MATLAB, as shown in Fig.4. The hollow diamond, the rectangle and the triangle in the figure, respectively, correspond to the polymer solutions with mass concentration of 500 mg/L, 1 000 mg/L and 1 500 mg/L.

Fig.4Intas functions ofnandt

Fig.5 Schematic diagram of converging capillary
3.1 Parameters of capillary model
In this paper, the converging capillary (Fig.5) and the converging-diverging capillary (Fig.6) are studied. Without special mentions, the parameter selection of the capillary is as follows: the lengthL=100μ m , in the converging capillaryRL=10μm , in the converging-diverging capillaryRmin=10μm .

Fig.6 Schematic diagram of converging-diverging capillary
3.2 Flow in contraction capillary
For the converging capillary shown in Fig.5, we have

θis the convergent angle, so

The pressure drop caused by the viscoelastic fluid flowing in the converging capillary includes 3 parts, namely, the shear pressure drop, the elastic pressure drop and the elongational pressure drop. Substituting Eq.(24) into Eqs.(20), (21) and (22), we can obtain the following equations:
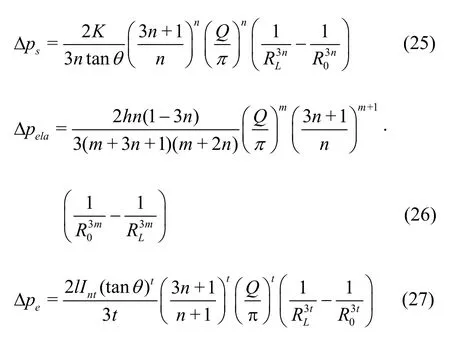
For the Newton fluid, there is no flexibility, therefore, Δpela=0. The situation discussed in this paper can be seen as in a uniaxial tension. According to the Trouton ratio, the elongational viscosity of the Newtonian fluid is three times of the shear viscosity. While 3K=l=3μ,n=t=1 , the shear pressure drop and the elongational pressure drop of the Newton fluid can be expressed as

After deformation, Eq.(28) is the same as the pressure drop equation of the Newtonian fluid while flowing in a gradually converging capillary given by Bird[14]. But due to the elongational deformation in the converging capillary, the total pressure drop should also include the elongational term, namely, as in Eq.(29).
According to Eq.(28) and Eq.(29), we obtain the ratio of the elongational pressure drop gradient to the shear pressure drop gradient

The total pressure drop gradient is as follow

Equation (30) shows that, along with the increase of the convergent angle, the ratio of the elongational pressure drop gradient to the shear pressure drop gradient also increases. And for whatever the capillary radius, its contribution to the total pressure drop is the same whenθ=35.26o. Ifθ>35.26o, the pressure drop caused by the stretching begins to dominate.
Equation (31) shows that the total pressure drop gradient is a function of the flow rate, the viscosity, the capillary radius and the convergent angle. In order to study the effect of the convergent angle on the total pressure drop gradient, the fluid viscosity is fixed as 1 mPa·s, the rate of flowQ=5.0× 10-15m3/s ,R0=50μm ,RL=10μm . With various convergent angles, the corresponding total pressure drop gradients can be calculated. In fact, the convergent angle is adjusted by changing the length of the capillary. But with different the lengths, the average capillary radius is the same.
Figure 7 shows the change of the shear pressure drop gradient, the elongational pressure drop gradient and the total pressure drop gradient along with the convergent angle calculated by Eq.(28) and Eq.(29). It can be seen that with the same flow rate, the shear pressure drop gradient does not change with the convergent angle. But as the convergent angle increases, the stretching rate increases and the elongational viscosity increases. So, as a mass, the elongational pressure drop gradient increases with the increase of the convergent angle. When the convergent angle is nearo35, the contributions of the pressure drops caused by the shear stress and the elongational stress to the total pressure drop tend to be equal. The total pressure drop gradient increases with the increase of the convergent angle. When the convergent angle iso45, the elongational pressure drop accounts for two-thirds of the total pressure drop, the total pressure drop increases with the increase of the convergent angle, as is very close to the conclusion of Durst[15-20], namely, the pressure drop of the viscous fluid in the porous media is produced by 25% of the pressure drop caused by the shear stress and 75% of that caused by the elongational stress.

Fig.7 Pressure drop gradients (Δp/Δl) for flow of Newtonian fluid through converging tube as a function ofθ
Equations (28) and (29) show that both the shear pressure drop and the elongational pressure drop are proportional to the flow rate. For a capillary of a particular size, the curve of the flow pressure differential is a straight line through the origin. But for a viscoelastic fluid, the seepage law is more complicated, the flow rate and the differential pressure are controlled by multiple factors in a comprehensive way. The polymer solutions in table 1 are with three mass concentrations of 500 mg/L, 1 000 mg/L and 1 500 mg/L. The contributions of the shear, elastic and elongational movements to the total pressure drop in a converging tube can be analyzed by studying these solutions. The pressure drop can be, respectively, calculated by Eqs.(25), (26) and (27), the result is shown in Fig.8. The convergent angle of the capillary model is 20o.

Fig.8 Shear, extensional and total pressure drop gradients for flow of various concentrations polymer solutions through converging tube withθ=20o
The solid point in Fig.8(a) stands for the elongational pressure drop gradient (C), and the hollow point stands for the shear pressure drop gradient. The figure shows that the polymer solution’s shear pressure drop gradient increases with the increase of the flow rate, while the elongational pressure drop gradient (D) increase along with the increase of the flow rate. When the fluid flow rate is beyond a critical value, the elongational pressure dropʼs contribution to the total pressure drop (M) will be larger than that of the shear pressure drop. The critical value depends on the shear and elongational properties of the polymer solution and the capillary shape, as the physical parameters of the pore medium. The critical flow rateQcis as follow
where
According to Eq.(32), the critical flow rate of the polymer solutions of the three kinds in the capillary with different convergent angles is calculated, as shown in Table 2. For the actual need, the flow rate isconverted into the average flow velocity of international unit.
As shown in Table 2, the critical velocity decreases with the increase of the convergent angle. This is because with the same velocity, the larger the convergent angle, the greater the extension rate, therefore the elongational viscosity will be higher, which makes the elongational pressure drop increase faster and can be equal to the shear pressure drop at a lower flow rate.

Table 2 Critical average flow velocity for polymer solution (10-2m/s)
Calculation result of the elastic pressure drop shows that, when the polymer solution flows through a contractive capillary, the contribution of its elastic pressure drop caused by the first normal stress to the total pressure drop takes a negative value. On the contrary, when it flows in an expanding capillary, the elastic pressure drop is positive. With a low flow rate, the difference between the elastic pressure drop and the total pressure drop is 3-4 orders of magnitude, and the elastic pressure drop can be neglected. But the absolute value of the elastic pressure drop also increases with the increase of the flow rate, so in the area near the wellbore, because of the large seepage velocity, the shear rate and the elongational rate are both very high, The proportion of the elastic pressure drop will be increased.
Figure 8(b) shows the change of the total pressure drop gradient (including the elastic pressure drop) of polymer solutions with different mass concentrations in a converging capillary whoseθiso20 along with the change of the flow rate. The calculation results follow the general law of the polymer solution seeping in the core. The figure shows that while the solution composed of the same type of polymer flows through the same converging capillary, the increase of the seepage pressure drop of a high concentration polymer solution along with the increase of the flow rate is also larger. Especially under the condition of a high speed flow, the linear relationship is not valid, which is the performance of the viscoelastic polymer solution’s strong elongational property.
3.3 Flow in converging-diverging capillary
The contraction and expansion sections of the converging-diverging capillary in Fig.6 are of the same size. Analysis shows that the shear pressure drop and the elongational pressure drop of the fluid in the contraction section are equal to the pressure drops in the expansion section. At the same time, due to the sizes of the inlet and the outlet of the convergingdiverging capillary are the same, for a viscoelastic fluid, the pressure drop produced by the first normal stress difference is zero.
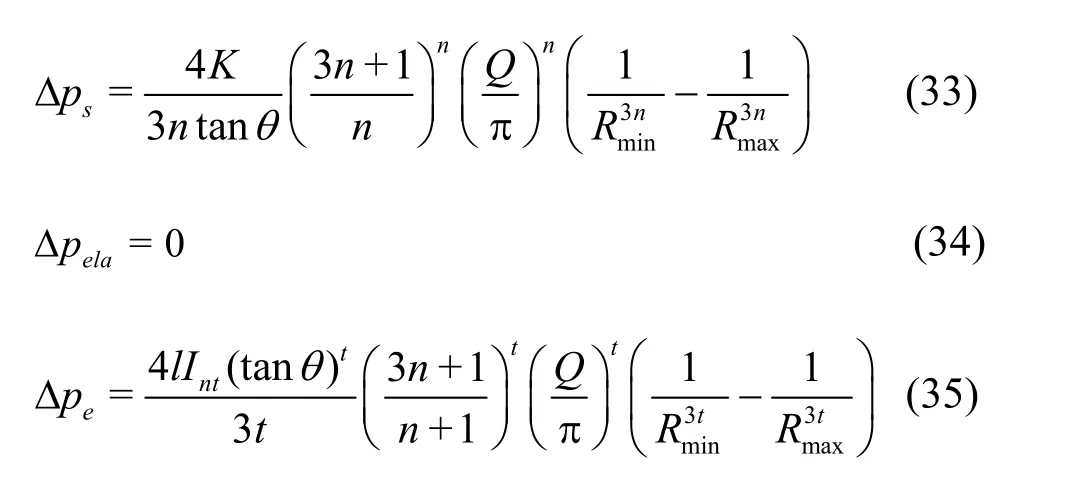

Fig.9 Shear, elongational and total pressure drop gradients for flow of various concentrations of polymer solutions through converging-diverging tube withθ=20o
Figures 9(a) and 9(b) show the curve of the extensional pressure and total drop gradient, the elongational pressure drop gradient and the total pressure drop gradient along with the flow rate of the polymer solution with concentrations of 500 mg/L, 1 000 mg/L and 1 500 mg/L flowing through theconverging-diverging capillary with the convergent angle ofo
20. Compared with the contraction capillary with the same contract angle, with the same flow rate, the pressure drop gradient is about 100 percent higher. The average radius of the contraction capillary is larger than that of the converging-diverging capillary, which is the main reason.

Fig.10 Shear and elongational pressure drop gradients for flow of various concentrations of polymer solutions through converging tube and converging-diverging tube withθ=20o
By comparing the shear and elongational pressure drop gradients of various concentrations of polymer solutions through the converging tube and the converging-diverging tube withθ=20o, which are shown in Figs.10(a) and 10(b). It can be seen that both the shear pressure drop gradient and the elongational pressure drop gradient of the converging-diverging tube are larger than those of the converging tube. The larger the concentration is, the larger the gap between the two kinds of tube.
4. Flow of viscoelastic fluid in porous media
We believe that the porous medium is composed of multiple sinusoidal capillary bundles (as shown in Fig.11).

Fig.11 Schematic diagram of sinusoidal capillary
The sinusoidal capillary can be expressed as follows

Substituting Eq.(26) into Eq.(24) and Eq.(36), and assuming that 3K=l=3μ,n=t=1, the shear pressure drop and the elongational pressure drop of Newtonian fluid flowing in the sinusoidal capillary can be obtained as

As the inlet and outlet radii of the sinusoidal capillary are the same, for the polymer solution, we have Δpela=0. The shear pressure drop and the elongational pressure drop are as follows:
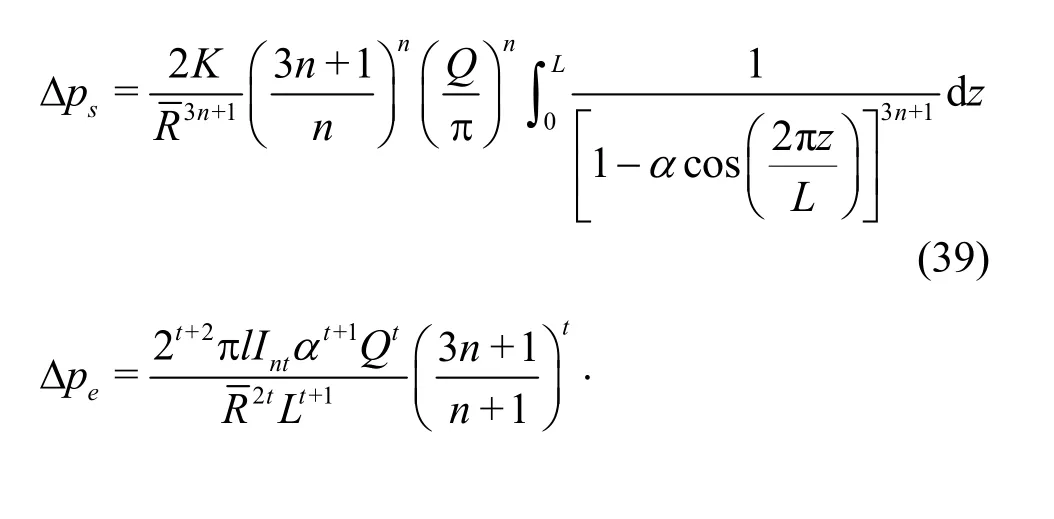

For the viscoelastic fluid, when only considering the shear flow, by Eq.(39), the average flow velocityinNcapillaries can be obtained as

In Eq.(41), the average particle diameter is used to replace the average radiusThe apparent velocity of the porous media is

whereL′=NL,τis the tortuosity.
By Eq.(42), the shear pressure drop gradient of the porous medium can be represented as

When only considering the elongational flow

The equation is written in a similar form as

The total pressure drop gradient in the case of flowing through the porous medium is

The coefficientsaandbneed to be determined through the indoor experiment.

Fig.12 Pressure drop vs. flow rate for PAA solution
Koshiba et al.[21]measured the pressure drop of the PAA of the mass concentration of 1.0% flowing in the packed bed P1 along with the flow rate through the indoor experiment (Fig.12). The power-law index of the PAA solution of a mass concentration of 1.0% takes a value of 0.3. According to the relationship between the elongational viscosity and the elongational rate, the elongational index is regressed to be 1.58. With the regression type (41), the experimental data is found to be fitted with this method very well, which verifies that the pressure drop gradient of the viscoelastic fluid flowing in the porous media is consistent with the type (41).
5. Conclusions
(1) The pressure drop formula for the viscoelastic polymer solution flowing in an abrupt contraction capillary is obtained based on the Binding’s minimum energy principle, and the polymer solution of the mass concentration of 1 000 mg/L is especially considered. The results show that the inlet pressure drop gradient and the average pressure drop gradient increase along with the pore throat ratio, the ratio of the two pressure drop gradients first increases with the increase of the pore throat ratio and then decreases, and the ratio is only related to the pore throat ratio.
(2) The inlet pressure drop gradient and the average pressure drop gradient of the viscoelastic polymer solution in an abrupt contraction capillary first sharply decrease with the increase of the throat radius, and then level off. That means that, if the throat radius is too small, the flow resistance will rapidly be aggrandized.
(3) On the basis of the Binding’s work, the relationship between the pressure difference and the flow rate of the viscoelastic polymer solution in capillaries of slowly changing diameter along the axial direction is obtained. The capillary models include the gradual contraction capillary and the converging-di-verging capillary.
(4) The elastic pressure drop produced by the first normal stress difference is only related to the radii of the two ports. For the polymer solution studied in this paper, the elastic pressure drop is several orders of magnitude smaller than those of the shear and elongational pressure drops and it can be ignored.
(5) The elongational pressure drop of the viscoelatic polymer solution in a capillary of variable cross-section increases along with the increase of the convergent angle of the gradual contraction capillary and the converging-diverging capillary. There exists a critical flow rate value, if the flow rate is beyond that value, the pressure produced by the elongational stress will be larger than the shear pressure drop. The value depends on the rheological parameters of the polymer solution and the properties of the porous media.
(6) Instead of the straight pipe, we consider the corrugated pipe model to establish the seepage model of the viscoelastic fluid flowing in the porous media. Under the condition that the rheological parameters of the polymer solution is known, the pressure drop of the viscoelastic fluid flowing in the porous media can be predicted with the model.
[1] Petrie C. J. S. One hundred years of extensional flow [J].Journal of Non-Newtonian Fluid Mechanics, 2006, 137(1-3): 1-14.
[2] Petrie C. J. S. Extensional viscosity: A critical discussion [J].Journal of Non-Newtonian Fluid Mechanics, 2006, 137(1-3): 15-23.
[3] Liang J. Z. Quantitative description of entry converging flow of polymers [J].Special Purpose Rubber Products, 2004, 25(3): 29-32(in Chinese).
[4] Wever D. A. Z., Picchioni F., Broekhuis A. A. Polymers for enhanced oil recovery: A paradigm for structureproperty relationship in aqueous solution [J].Progress in Polymer Science, 2011, 36(11): 1558-1628.
[5] Shen M. X. Synthesis and adhesion of polymeric hydrogels [D]. Doctoral Thesis, Shanghai, China: East China University of Science and Technology, 2014(in Chinese).
[6] Dressler M. Shear flow properties of polymer blend models with and without droplet inertia [J].Journal of non-Newtonian Fluid Mechanics, 2013, 200: 147-167.
[7] Feng S. D. Study on controlling factors of viscosity of polymer solution in Daqing Oilfield [D]. Doctoral Thesis, Daqing, China: Northeastern Petroleum University, 2013(in Chinese).
[8] Forest M. G., Heidenreich S., Hess S. et al. Dynamic texture scaling of sheared nematic polymers in the large Ericksen number limit [J].Journal of Non-Newtonian Fluid Mechanics, 2010, 165(13): 687-697.
[9] Sienz J., Bates S. J., Pittman J. F. T. Flow restrictor design for extrusion slit dies for a range of materials: Simulation and comparison of optimization techniques [J].Finite Elements in Analysis and Design, 2006, 42(5): 430-453.
[10] Liang F., Bao R. D., Jin Y. et al. Dynamic stability of a fluid-conveying carbon nanotube embedding in linear viscoelastic medium [J].Journal of Vibration and Shock, 2015, 34(1): 140-144.
[11] Habla F., Obermeier A., Hinrichsen O. Semiimplicit stress formulation for viscoelastic models: Application to threedimensional contraction flows [J].Journal of Non-Newtonian Fluid Mechanics, 2013, 199: 70-79.
[12] Kozdon J. E., Mallison B., Gerritsen M. et al. Multidimensional upwinding for multiphase transport in porous media [J].Society of Petroleum Engineers, 2011, 16(2): 263-272.
[13] Tian Z. P., ZHANG B., CUI H. Q. etal. Mathematical model and numerical calculation for viscoelastic fluid flow through fractal porous media [J].Acta Petrolei Sinica, 2014, 35(1): 118-122(in Chinese).
[14] Binding D. M., Phillips P. M., Phillips T. N. Contraction/expansion flows: The pressure drop and related issues [J].Journal of Non-newtonian Fluid Mechanics, 2006, 137(1-3): 31-38.
[15] Yang F. L. Mechanism of polymer flooding and a new enhanced oil recovery ofhigh-concentration polymer flooding [D]. Doctoral Thesis, Daqing, China: Daqing Petroleum Institute, 2004(in Chinese).
[16] Zhang H. F., Wang D. M., Wang L. J. Flow laws of polymer solution in porous media and their mechanism on enhancing displacement efficiency [J].Petroleum Geology and Oilfield Development in Daqing, 2002, 21(4): 57-60(in Chinese).
[17] Xia H. F., Wang D. M., Liu Z. C. Study on the mechanism of polymer solution with visco-elastic behavior increasing microscopic oil displacement efficiency [J].Acta Petrolei Sinica, 2001, 22(4): 60-65(in Chinese).
[18] Wang D. M., Chen J. C., Yang Q. Y. Viscous-elastic polymer can increase micro-scale displacement efficiency in cores [J].Acta Petrolei Sinica, 2000, 21(5): 45-51(in Chinese).
[19] Baag S., Acharya M. R., Dash G. C. et al. MHD Flow of a visco-elastic through a porous medium between infinite parallel plates with time dependent suction [J].Journal of Hydrodynamics, 2015, 27(5): 738-747.
[20] Hayat T., Awais M., Obaidat S. Similar solution for threedimensional flow in an Oldroyd-B fluid over a stretching surface [J].International Journal for Numerical Methods in Fluids, 2012, 70(7): 851-859.
[21] Koshiba T., Hashimoto T., Mori N. et al. Pressure loss of viscoelastic surfactant solutions under the flow in a packed bed of particles [J].Journal of the Society of Rheology, 2007, 35(1): 21-26.
(Received May 7 2015, Revised November 11, 2015)
* Project supported by the National Natural Science Foundation of China (Grant No. 51574085), the Natural Science Founaation of Heilongjiang Province (Grant No. F2015020) and the Science and Technology Research Project of Department of Education of Heilongjiang Province (Grant No. 12521059).
Biography:Er-long Yang (1976-), Male, Ph. D., Professor
Mei Wang,
E-mail: wmmay@sina.com
- 水动力学研究与进展 B辑的其它文章
- ICHD’ 2018 The 13th International Conference on Hydrodynamics First Announcement
- Cavitation erosion in bloods*
- A GPU accelerated finite volume coastal ocean model*
- Mixing features in an electromagnetic rectangular micromixer for electrolyte solutions*
- A numerical study of violent sloshing problems with modified MPS method*
- Numerical investigation of entropy generation and heat transfer of pulsating flow in a horizontal channel with an open cavity*

