全球高程系统的统一问题

许厚泽

中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，湖北 武汉 430077

全球高程系统的统一问题

许厚泽

中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，湖北 武汉 430077

Global Unification Problem of the Height System

XU Houze

State Key Laboratory of Geodesy and Earth’s Geodynamics，Chinese Academy of Sciences, Wuhan 430077, China

讨论了建立全球统一高程系统的若干基本问题，包括正常高的几何定义和重力定义，区域水准测量高程系统的全球统一问题以及大地水准面位W0的确定。结果表明：①几何水准高程和重力定义的正常高存在差别，由GNSS/重力得到的正常高并不等于几何水准给出的正常高，而要加上一与高程有关的改正项，并且在山区这一改正不可忽略；②由GNSS/重力/区域几何水准融合可以给出一个相对的全球统一高程系统，而要得到绝对的统一系统，还须知道大地水准面的位W0；③现代大地测量技术可以以一定精度求出W0，但它是时变的，因此只能定义出某个历元的全球绝对统一高程系统。

高程系统；正常高；大地水准面位

1 正常高的几何定义和重力定义

目前，高程测量中的正常高可以从两种方法得到：一是传统的水准测量方法；二是以GNSS观测中得到大地高h，从重力测量中给出高程异常ζ，由两者之差求得正常高H=h-ζ。反过来也可以从GNSS/水准结合重力测量来精确确定区域似大地水准面。通常，在国内外文献中，均认为这两种方法给出的正常高是完全相等的，但是严格地讲，这两者从理论上是有差别的，也就是说，重力和水准定义的正常高是不一致的。

1.1 重力学定义的正常高[1]

(1)

图1 高程系统的定义Fig.1 The definition of height system

根据莫洛金斯基理论，A′点的选取满足以下条件

UA′-U0=WA-W0

(2)

显然，似大地水准面不是一个等位面。根据条件式(2)，有

(3)

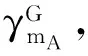
(4)

于是重力学定义的正常高

(5)

(6)

由条件式(2)，定义扰动位

(7)

这里W0、U0分别为大地水准面和正常水准椭球面上的位，就静态问题而言，可视为一常数，由于在选择正常地球椭球体时，要求U0≈W0，因此W0-U0是一微小量，可足够近似地在式(7)中以γ0(正常地球椭球面上γ的平均值)取代γA。于是有

(8)

式中，TA可根据重力测量边值问题的解，由重力异常值Δg按Stokes-Molodensky公式求得。需要指出的是，通常在讨论该问题时，从边界条件到解算都是球近似解。理论上还应考虑到扁率项的修正，但由于目前常应用所谓“移去-恢复”技术，需要处理的是扣除重力场模型的残差重力异常和高程异常，于是扁率项影响可以忽略不计。

1.2 几何水准定义的正常高

水准测量中正常高的定义是由正高的概念演化而来的，由于正高系统中平均重力值gmA难以精密测定，莫洛金斯基于1945年提出用正常重力的平均值γmA来代替[1]，从而给出几何水准定义的正常高，即

(9)

(10)

将式(9)中的水准测量路线上的重力g写为

(11)

式中，γ为水准路线上地面点的正常重力，以足够的近似可假设正常重力随高程线性变化，于是有

(12)

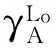
(13)

而水准路线上的两点的高程应为

(14)

式中，ε为正常位水准面不平行引起的高差改正项；λ为扰动重力高差改正项。经推导[2]，有

(15)

(16)

以及

(17)

式中，hAB为A和B两点的概略高程差，这就是当前我国水准测量规范所实行的改正。

比较式(5)和式(9)可以看出，重力定义的正常高和几何水准定义的正常高是不相同的，其区别在于使用的正常重力平均值是不同的，重力定义用的是近似地表面点到地球椭球点A′A0的平均，几何水准定义用的是地球表面点到几何水准起算面点AA2的平均，两种定义的正常高之差为

(18)

(19)

式中，ζ单位为m;γ单位为mGal。代入式(18)有

(20)

(21)

其单位为m，还要注意的是，GNSS和重力ζ的地球椭球参数应保持一致。

2 区域全球高程系统的转换

为此，国际大地测量协会(IAG)实行的全球大地测量观测系统(GGOS)计划中明确提出，要建立全球与重力相关的全球垂直参考系统[3]，其目的是：

(1) 支持厘米级高精度全球物理和几何高程系统的统一。

(2) 统一现存的所有区域高程系统。

(3) 保证全球的一致性和长期稳定性(任何地方、任何时间有同等精度)。

全球高程系统的统一与以下两个重要参数相关：

(1) 在水准测量中，由于区域高程零点选在水准测量起始点(G点，例如青岛验潮站的平均海平面)，而非O点(大地水准面上的点，见图1)，因此人们只能测量出由G到A的位差，即

(22)

于是区域系统水准测量所给出的正常高将为

(23)

(24)

(2) 在重力正常高解算中，对于W0≠U0时，须考虑W0-U0的影响。注意到式(7)和式(21)，式(24)可写成

(25)

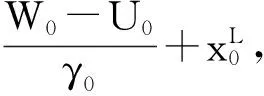
3 大地水准面位W0的确定

大地水准面是反映地球内部质量分布和运动的等位面，其定义可以是：

(1) 物理上现实存在的实际大地水准面。其定义为在最小二乘意义下，与全球海洋上各点的静止平均海水面相一致的等位面，这样定义的现实大地水准面是时变的。

(2) 仅具理论意义的理论大地水准面。按照重力学，其定义为与选定的地球椭球面上正常位U0相等的等位面，即W0=U0，这样定义的理论大地水准面是静态的，其位值W0唯一的由地球椭球的几何与物理参数确定a(长半径)，J2(动力学扁率)，GM(万有引力常数与地球质量的乘积)及ω(地球旋转角速度)确定

(26)

式中，e为椭球第一偏心率，可根据a、J2以及GM由式(27)迭代求出

(27)

现代大地测量技术的发展已使人们可以利用卫星定位、卫星测高以及重力位的观测确定出实际的大地水准面位值W0，按大地水准面的定义，有

(28)

这里SST为海面地形，积分沿整个地球的海域S

式中，j为海面上的某点，γj为其正常重力值。

(29)

迄今，国际大地测量学会(IAG)所属垂直基准标准化工作组，根据上述方法确定的大地水准面位的参数值为[8,9]

W0=62 636 854.2±0.2 m2s-2(epoch：2005.0)

(30)

并且发现，不同的MSS模型及积分海域S对此位值的确定影响较大，而不同的重力场模型则影响很小，此外，采用不同的潮汐系统与结果无关。但要特别指出的是，由式(29)确定的W0使用的MSS资料是与所使用的大地坐标系统有关的，式(30)的值是在WGS-84系统中给出的。同时，计算表明，大地水准面位W0还是时变的，其值为[8]

(31)

(32)

按式(26)及式(30)

U0=62 636 851.67 m3s-2

(33)

由我国GNSS、水准及重力得到的我国85黄海高程系统相对于全球绝对高程系统的系统差为[10]

(34)

4 讨 论

通过上面的分析，本文得到如下的认识:

(1) 正常高的几何定义和重力定义是不一样的，在融合GNSS、水准及重力资料进行区域似大地水准面精化时要考虑其差别，加上与高程有关的改正项。

(2) 把区域的水准测量高程系统转换到全球统一的高程系统。需要确定常数x0及W0-U0，在假定W0=U0时，x0可以由GNSS/重力/水准定出。即可以建立一个相对的全球统一高程系统。

(3) 要确定相对和绝对全球统一高程系统的系统差，需要测定大地水准面的位值W0，W0值可以用现代大地测量技术确定。它是时变的，与观测的历元以及选用的大地坐标系统有关。

[1] HEISKANEN W A, MORITZ H. Physical Geodesy[J]. Bulletin Géodésique, 1967, 86(1): 491-492.

[2] 党亚民, 章传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015. DANG Yamin, ZHANG Chuanyin, CHEN Junyong, et al. Modern Geodetic Datum[M]. Beijing: Surveying and Mapping Press, 2015.

[3] KUTTERER H, NEILAN R, BIANCO G. Global Geodetic Observing System (GGOS)[J]∥Journal of Geodesy, 2012, 86(10): 915-926.

[4] FÖRSTE C, BRUINSMA S, SHAKO R, et al. EIGEN-6—A New Combined Global Gravity Field Model Including GOCE Data from the Collaboration of GFZ-Potsdam and GRGS-Toulouse[R]. [S.l.]: [s.n.], 2011.

[5] LEMOINE F G, KENYON S C, FACTOR J K, et al. The Development of the Joint NASA GSFC and the NIMA Geopotential Model EGM96[J]. 1998.

[6] MENEMENLIS D, CAMPIN J M, HEIMBACH P, et al. ECCO2: High Resolution Global Ocean and Sea Ice Data Synthesis[C]∥AGU Fall Meeting. [s.l.]: AGU, 2008.

[7] 赫林, 李建成, 褚永海. 1985国家高程基准与全球高程基准之间的垂直偏差[J]. 测绘学报, 2016, 45(7): 768-774. HE Lin, LI Jiancheng, CHU Yonghai. The Vertical Shift Between 1985 National Height Datum and Global Vertical Datum[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 768-774. DOI: 10.11947/j.AGCS.2016.20160029.

[8] DAYOUB N, EDWARDS S J, MOORE P. The Gauss-listing Geopotential ValueW0and Its Rate from Altimetric Mean Sea Level and GRACE[J]. Journal of Geodesy, 2012, 86(9): 681-694.

[10] ZHANG Chuanyin, DANG Yamin, JIANG Tao, et al. Heterogeneous Gravity Data Fusion and Gravimetric Quasigeoid Computation in the Coastal Area of China[J]. Marine Geodesy, 2017, 40(2-3): 142-159.

[11] 翟振和, 李达, 欧阳明达. 大地水准面重力位的确定[J]. 测绘科学与工程, 2015, 35(1): 14-18. ZHAI Zhenhe, LI Da, OUYANG Mingda. Determination of Gravity Potential of the Geoid[J]. Geomatic Science and Engineering, 2015, 35(1): 14-18.

(责任编辑：陈品馨)

Author： XU Houze(1934—), male, academician,majors in the areas of geodesy and geophysics including gravimetry and solid earth tide.

E-mail： hsuh@asch.whigg.ac.cn

欢迎订阅《测绘学报》

《测绘学报》创刊于1957年，是由中国科协主管、中国测绘地理信息学会主办、《测绘学报》编辑部编辑、测绘出版社出版的反映我国测绘地理信息科学技术发展水平的综合性学术刊物，影响因子和被引频次居中文核心期刊测绘地理信息类前列，是美国《工程索引》 (Ei)核心期刊，曾荣获百种中国杰出学术期刊、中国精品科技期刊、中国国际影响力优秀学术期刊、全国优秀测绘期刊等称号，连续多年入选中国科协精品科技期刊工程项目，并被国内外多个重要数据库收录，是我国测绘地理信息科学领域具有重要影响力的学术期刊。

《测绘学报》着重报道我国测绘地理信息科技最新的重要研究成果及其应用，内容涉及大地测量与导航、工程测量、摄影测量与遥感、地图学与地理信息、矿山测量、海洋测绘、地籍测绘、地图印刷、测绘仪器、信息传输等测绘地理信息学科及其相关相邻学科。

《测绘学报》设有综述、快报论文、学术论文、博士论文摘要等栏目。

《测绘学报》(月刊)2017年定价：40.00元/期,邮发代号：2-224。

编辑部地址：北京市西城区三里河路50号，邮编：100045，订阅电话：010-68531192(金老师)，010-68531317(传真)。

网址：http:∥xb.sinomaps.com

许厚泽.全球高程系统的统一问题[J].测绘学报，2017,46(8)：939-944.

10.11947/j.AGCS.2017.20170406. XU Houze. Global Unification Problem of the Height System[J]. Acta Geodaetica et Cartographica Sinica,2017,46(8):939-944. DOI:10.11947/j.AGCS.2017.20170406.

P

A

1001-1595(2017)08-0939-06

2017-07-17

许厚泽(1934—)，男，中国科学院院士，主要从事地球重力学、地球固体潮等大地测量与地球物理学科方面的研究工作。

修回日期： 2017-08-10