大跨度PC连续梁桥预应力管道摩阻试验研究

牛黎明

（甘肃长达路业有限责任公司，甘肃 兰州 730050）

大跨度PC连续梁桥预应力管道摩阻试验研究

牛黎明

（甘肃长达路业有限责任公司，甘肃 兰州 730050）

针对预应力混凝土梁管道摩阻损失测试的必要性和重要性，介绍了预应力管道摩阻损失的测试原理和方法。应用最小二乘法原理，由规范中的公式推导预应力管道摩阻系数μ和偏差系数k的算式，结合某大跨预应力混凝土连续箱梁桥预应力管道摩阻的现场测试，计算出实际预应力管道摩阻系数，并与设计值和规范值比较，分析了测试方法的合理性和试验结果的可靠性。

预应力混凝土；管道摩阻系数；管道偏差系数；最小二乘原理

0 引言

预应力混凝土结构，尤其是预应力混凝土桥梁结构中，预应力损失值直接关系到预应力钢筋中的有效预应力是否满足结构使用阶段的要求。而预应力损失的五个主要因素（混凝土收缩徐变、预应力筋松弛、锚头变形及预应力筋回缩、摩阻、混凝土弹性压缩）中，摩阻的损失所占比例很大，尤其是对弯曲长束管道的摩阻损失可达40%以上[1]。所以，设计要求在预应力混凝土梁正式张拉前，应对结构进行管道摩阻现场测试，并根据测试结果对张拉力及管道进行调整，将设计张拉力准确施加至梁体。管道摩阻损失是后张预应力混凝土梁的预应力损失的主要部分之一，对它的准确估计将关系到有效预应力是否能满足梁使用要求，影响着梁体的预拱变形，在某些情况下将影响着桥梁的整体外观等。过高的估计会使得预应力张拉过度，导致梁端混凝土局部破坏或梁体预拉区开裂，且梁体延性会降低；过低的估计则不能施加足够的预应力，进而影响着桥梁的承载能力、变形和抗裂度等。

工程中对预应力管道摩阻损失采用管道摩阻系数μ和管道偏差系数k来表征。大跨度预应力混凝土箱型梁桥需施加的预应力以及施加后在结构中所产生的有效预应力的确定是保证预应力结构安全性能的关键，而相关设计规范中只提供了一般条件下预应力的摩阻损失数据，对于大曲率预应力筋混凝土结构，其管道摩阻损失都必须进行专门的管道摩阻试验测试[2-5]。本文通过对某特大预应力混凝土连续梁桥纵向预应力束管道摩阻的现场测试，计算出实际预应力管道摩阻系数，并与设计值和规范值比较，进而分析测试方法的合理性和试验结果的可靠性。

1 预应力管道摩阻基本理论

1.1 管道摩阻

预应力箱梁采用后张法张拉工艺时，预应力钢筋布置一般分为直线布置和曲线布置两种。因此管道摩阻引起的预应力损失可分为长度影响和弯道影响，即管道偏差效应和曲率效应。理论上讲，直线管道无摩擦损失，但由于施工时因振动等原因而使管道变成波形，加之预应力筋因自重下垂，与管道有实际接触，故当张拉预应力筋有相对滑动时就会产生摩阻力，此项称为管道走动影响（或偏差影响、长度影响）。对于管道弯转影响除了管道走动影响之外，还有力筋对管道内壁的径向压力所产生的摩阻力，该部分称为弯道影响，随力筋弯曲角度的增加而增加。因此曲线管道的摩擦损失应为管道偏差效应与曲率效应之和[4]。

1.2 计算公式推导

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTGD 62-2004）第6、2、2条规定[2]，后张法构件张拉时，预应力钢筋与管道壁之间摩擦引起的预应力损失，可按下式计算：

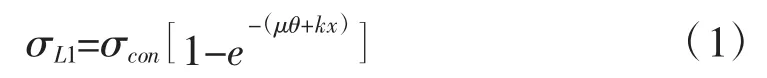
式中：σcon为预应力钢筋锚下的张拉控制应力（MPa）；θ为从张拉端至计算截面曲线管道部分切线的夹角之和（rad）；x为从张拉端至计算截面的管道长度，可近似取该管道在构件纵轴上的投影长度（m）；μ为预应力钢束与管道壁的摩擦系数；k为管道每米局部偏差对摩擦的影响系数。

设张拉端传感器测试值为FZ，锚固端传感器测试值为FB，此时为管道长度l，θ为管道全长的曲线包角，则式（1）可写为：

对式（2）两边取对数得：

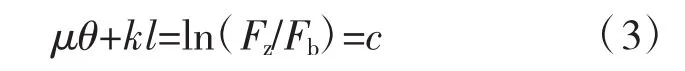
一般情况下，预应力施工采用一种制孔方法，这时管道质量比较均匀，可以不考虑摩阻系数μ和k变异。由于设计和实际施工存在差异，故不可避免的产生误差，假设误差为Δ，即：

若有n束预应力钢束，则：

利用最小二乘法原理，全部预应力钢束误差的平方和为：

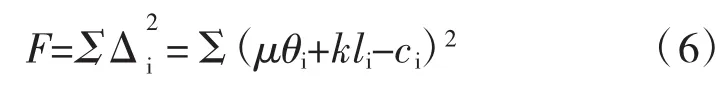
欲使试验误差最小，应使

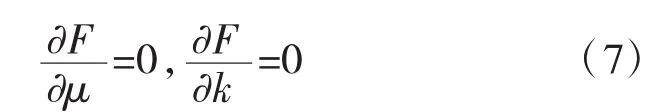
由式（7）对式（6）求导，并整理得：

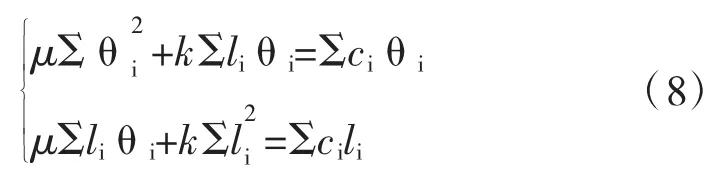
根据式（8）可求得参数μ和k。需要指出的是，由于μ和k是相互耦联的，故试验中必须至少测试2束以上的预应力钢束才能计算出μ和k。

2 管道摩阻测试

图1为管道摩阻试验布置图，所需试验仪器、设备可见图1。试验时采用一端张拉，也就是说，仅主动端用千斤顶进行张拉，被动端不张拉，并在主动端和被动端各设一台应变仪，以精确测出张拉过程中两端的应变，从而求出应力。在此基础上，可计算出预应力损失大小，进而再反算出管道摩阻系数。

图 1管道摩阻试验布置图

本次测试中，在177＃墩1＃块选择一个直线管道T1和一个曲线管道W1（腹板束）共2个测试管道，每个管道内选择2根预应力钢绞线作为测试束。测试束在箱梁横断面及沿桥纵向的位置示意分别见图2、图3。

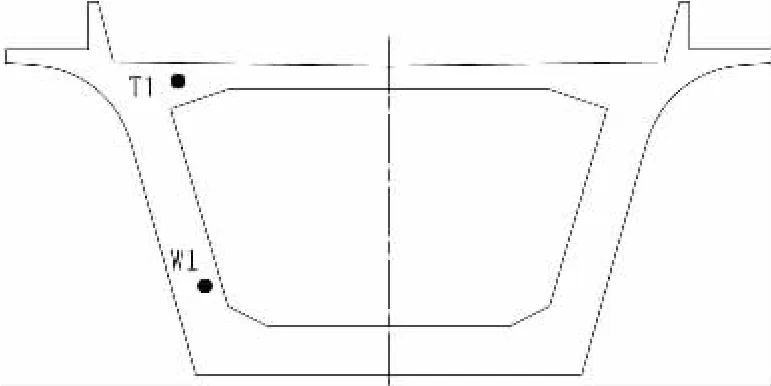
图2 测试束在横断面上的位置示意图

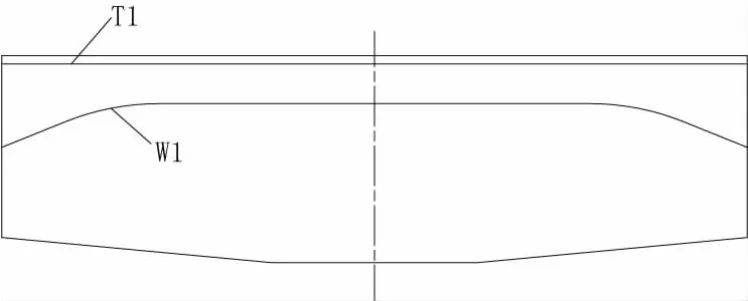
图 3测试束在沿桥纵向布置示意图

本试验共分3级加载，各级荷载分别为设计张拉控制应力的10%、30%和50%（即281.232 kN、843.696 kN和1 406.16 kN）。根据千斤顶油表读数控制张拉荷载级，同时校核传感器读数。安装传感器与千斤顶时，应确保两者中线位置与锚垫板保持一致，张拉时与钢绞线脱离接触。

3 测试结果分析

在177＃墩1＃块选取了一个直线束T1和一个曲线束W1，对每一束中的两根钢绞线粘贴应变片，作为测试对象。根据直线束T1按式（3）计算管道偏差系数k，根据分级张拉荷载即50%σcon所得测得的应变值进行计算。T1束测试结果分析见表1。

表1 T1束测试结果分析

根据表1可得管道偏差系数k=0.002 78，将直线束T1与曲线束W1组合，求出管道摩阻系数μ。因测试过程中张拉至50%σcon时因钢绞线摩擦导致测试线被拉断，故按张拉至30%σcon时测得数据进行分析。曲线束W1测试结果分析见表2。

表2 W1束测试结果分析

根据试验所得管道偏差系数k=0.002 78和管道摩阻系数μ=0.161，计算设计摩阻力与实测摩阻力的比值以及实测摩阻力与锚下控制应力的比值，见表3。原设计管道偏差系数k=0.002 5，管道摩阻系数μ=0.14。

表3 设计摩阻力/实测摩阻力与

设计摩阻力/实测摩阻力与实测摩阻力/锚下控制应力计算结果见表3，钢束设计伸长量、实测伸长量与计算伸长量计算结果见表4。

表4 钢束设计伸长量、实测伸长量

从以上试验结果可以看出：

（1）计算的预应力管道局部偏差影响系数值为0.002 78，管道摩阻系数为0.161，与设计值接近。

（2）设计管道摩阻力与实测管道摩阻力相差很小

（3）根据实测k，μ计算的钢束设计伸长量与原设计伸长量的偏差为-0.2 mm。

说明了试验方法的合理性和试验结果的可靠性。

4 结语

（1）管道摩阻损失是后张法预应力损失的重要组成部分，对其准确估计十分必要。

（2）本文采用的试验方法和最小二乘原理计算摩阻参数的方法合理可靠，简单易行。

（3）实际工程中，在预应力正式张拉前，应尽可能的进行现场测试以获取准确的摩阻参数，并根据实测结果进行施工控制。

（4）按最小二乘法计算实际预应力管道摩阻系数可以满足工程实际的需要，应选择数目不小于2的不同线形的预应力管道进行测试，选择的预应力管道应具有全面性、代表性，这样计算出的摩阻系数更与实际相符。

[1]杨孟刚,文永奎,陈政清.32m双线铁路简支箱梁管道摩阻试验研究[J].铁路标准设计,2001(11):3-4.

[2]JTGD 62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[3]GB 50010-2002,混凝土结构设计规范[S].

[4]王鹏,楼普增,范厚彬.悬臂浇筑施工中连续箱梁预应力管道摩阻测试研究[J].铁道建筑,2006(11):58-61.

[5]王强,何惟煌,林志春,等.后张预应力混凝土梁管道摩阻参数识别与分析[J].公路交通科技,2007,24(1):65-68.

U446

B

1009-7716（2017）08-0090-03

10.16799/j.cnki.csdqyfh.2017.08.027

2017-04-06

牛黎明（1983-），男，甘肃甘谷人，工程师，从事公路工程建设管理工作。