侧入式导光板网点半径分布函数及网点设计

周士康，周君玮，杜 金，陈春根

(上海三思科技发展有限公司 上海 201100)

侧入式导光板网点半径分布函数及网点设计

周士康，周君玮，杜 金，陈春根

(上海三思科技发展有限公司 上海 201100)

本文导出了单边、对边和四边进光的矩形导光板网点半径分布的实用函数表达式。其中单边进光导光板的半径分布函数是基于导光板的基本原理直接导出，对边和四边进光导光板的半径分布函数则是用改型的高斯函数由导光板的边条件求得的函数解。半径分布函数以物理意义明确的导光板参数如导光板的边长，边缘和中心网点半径为自变量，可以直接用于不同边长的矩形导光板的网点设计。为了进一步改善导光板的表面亮度的均匀性，本文还提出一种非常简单的新方法来优化网点位置的分布，称之为“局域随机化方法”。对三种进光情况的仿真和以对边进光为例的实际灯具的测量结果发光均匀度很好，证明本文的方法是一个成功的导光板设计方法。

导光板；侧入式；散射网点；网点设计; LED; 照明

引言

侧入式导光板相对于直下式导光板最大的优点是厚度薄、重量轻、成本低。目前，侧入式仍是导光板生产的主流型式，特别是中小尺寸导光板几乎全部是侧入式的。对侧入式导光板的研究一直没有停止过，包括新的模组设计方法[1]和新的工艺[2]。但侧入式导光板由于其光源位于边缘，因此易于造成导光板表面亮度不均匀，因此网点设计就成了侧入式导光板设计的关键所在。

对于侧入式导光板散射网点的设计，绝大部分厂家的都是给定一个经验网点分布，依赖商用光学仿真模拟软件，根据仿真和实测的结果不断人工修改规则分布的网点的大小或修改网点的分布位置。这样做的问题是效率较低、耗时长。为此许多网点工作[1-9]都试图从理论出发给出网点分布的数学计算模型。但这些理论工作绝大多数只对单边进光的导光板。而实际上大部分导光板如电脑、平板灯等稍为大一些的都是多边进光，不能用单边进光的理论。高双红等人[3]研究了多边进光的情况，其方法是四边进光时把矩形导光板分成四个小区域，但这就不可避免存在区域间的“边界效应”[8]，使得亮度不够均匀。庞晓峰用Tracepro对一个小尺寸的导光板进行了优化，提高了均匀度[10],但仍是从单边进光出发，应用范围较小。黄逸峰等提出基于模糊化理论的自动化设计的方法，但过程较复杂且只举了一维函数的例子[11]。

本文对单边、对边和四边进光的三种情况导出了网点半径的分布函数，这就可以一次性计算得到所有网点的半径。而且使用的自变量都是有明确物理意义的基本参数，如导光板的边长、边缘网点半径，实用性强。

对单边进光的情况，本文在推导基本公式的基础上，用边条件把公式变为以导光板边长和网点半径为自变量的实用公式。对于对边和四边进光的情况，我们提出用改型的高斯函数作为试探函数，用边条件来解得网点半径分布函数。这使得在各种情况下我们都有了网点半径分布的实用数学表达式，这就给导光板的设计工作带来了极大的方便。

网点分布位置的随机化可以进一步改善导光板的亮度均匀度。本文提出了一个非常简单有效的方法，称为“局域随机化方法”代替了目前较流行但比较复杂的如斥力缓和法和动态分子法。

由于决定侧光式导光板某处亮度的是该处网点的对光的散射程度，也就是网点的填充率(网点面积与其占有的面积的比)，因此只要控制填充率的分布，不管等半径而不等间距的网点或等间距而不等半径的网点都可以给出完全相同的结果。本文的方法采用的方案是等间距而不等半径的圆形网点，计算的结果是网点半径大小的分布，对于其他形状的印刷式或立体网点，本文的基本原理同样是可以使用的。

1 单边进光网点半径分布函数

对单边进光的情况，下面我们直接从导光板的基本原理出发推导出均匀出光要求下网点半径(r)和位置(x)的关系。

侧入式导光板中，进入导光板的光线在导光板中多次全反射不断向前传输，而导光板上的网点则改变了光线全反射的特性，使得照射在网点上的光线散射，由导光板的正面射出，导光板正面的光线就来自于这些散射光。

单边近光导光板内的光通量是单个自变量x的函数，设其为Φ(x)。由于不断散射，它是逐渐变小的，Φ(x)经过一个无限小的距离dx后其减少的部分可以用微分描述为-dΦ(x)。设单位长度散射到导光板外面的光通量为φ0，忽略吸收时光在经过dx长度后的损失部分-dΦ(x)当然就应该是散射到导光板外面的光φ0dx，这就得到了方程(1)：

(1)

我们希望导光板是均匀出光，因此φ0为与位置无关的常数。这样在经过距离x后，散射到导光板外的总光通量应该是φ0x，设起始光通量为Φ0，因此光通量Φ(x)是从Φ0开始随坐标x的增加而线性减少的，即

(2)

另一方面，散射光的多少应该与该处的光通量Φ(x)成正比，即

注意比例系数代表该处总光通量有多少散射出去了，它是一个与位置有关的函数，称为出光效率σ(x)：

(3)

把式(1)和式(2)代入式(3)得单边进光时出光效率函数为

(4)

值得注意的是我们的推导没有引入任何假定，仅仅是从导光板基本原理和均匀出光的要求出发而得到的，式(4)是一维导光板的基本公式。

对于圆形网点情况，设网格为间距是Δx的小正方形，则按照定义，填充率η(x)应该是园面积除以正方形面积，即

(5)

而出光效率显然是应该是正比于该处的填充率，设比例系数为k，即

(6)

由式(4)式(5)式(6)可得到了网点半径函数为

(7)

设矩形导光板长边的长度为2Lx，把坐标原点放在矩形正中心，则x的变化范围为-Lx到Lx，则出光效率函数(4)和网点半径分布函数(7)就分别变成为

(8)

(9)

文献[5-7]也得到了类似的单边进光导光板等直径网点分布公式。但由于是其参数k和φ0是未知的，在使用上很不方便。我们发现可以从导光板的边界条件出发可以把k和φ0消去，代之以网点半径和导光板长度，从而把分布函数式(9)变为更实用的公式。

首先把r(x)写成多元函数的形式：

(10)

其中r1和r2为x=-Lx和x=Lx时网点半径，以k和φ0为未知变量，由下列两个边条件联立方程求k和φ0的符号解：

(11)

可以得到

(12)

代入式(9)经简化后可以得到半径分布函数的表达式(13)。

(13)

式(13)就是最后的实用公式。由于联立方程式(11)的解式(12)已经把自变量给取代了，使得φ0和物理意义不清晰的k也消失了，自变量变成了物理意义清晰的r1,r2,Lx，这将十分有利于导光板设计。

注意到自变量Φ0自动消失了，这在物理意义上是很合理的结果，反映了起始光通量Φ0是一个相对值，不应该影响半径的分布。另外Δx也消失了，这反映了半径分布函数的连续性，即与网点间距Δx无关。还有，由式(12)还可以看到，要使得光通量φ0>0必须r2>r1，也就是离光源越远网点越大。以上这些数学和物理的一致性还可以在一定程度上反过来证明了我们所得函数的合理性。此外，所得公式的简单性，对称性也令人满意。

这样，只要给定r1,r2,Lx的具体数值，立刻就可以由式(13)得到网点分布函数。例如，对于半边长为50 mm，边缘网点半径为0.5 mm和1 mm的导光板，其网点半径的分布应该为函数r(x,0.5,1,50)，如图1所示。

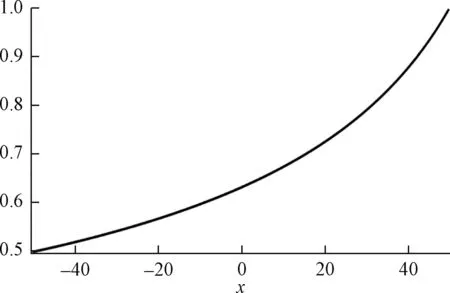
图1 单边进光导光板网点半径分布函数举例Fig.1 The dot radius distribution function of light guide plate with unilateral edge lighting

2 对边进光网点半径分布函数

对于对边进光的情况，考虑是否可以由单边进光推广到双边呢？基于非相干光的可叠加性原理，的确可以把通过网点散射出来的光通量分成两部分之和。这时，式(1)和式(2)应该分别对两部分成立，但是这样得到的是两个函数，而网点分布函数必须是一个。可见我们不能通过上面单边进光的公式推广从而求得对边进光时的通解。我们的解决方法是用一个试探函数求得在给定边条件下的一个特解，只要此解满足导光板是均匀出光的要求就可以了。

分析这一试探用的函数应该符合几个要求，一是离开光源越远则网点应越大，这是侧面进光导光板的一般规律；二是左右对称性，这是在对边进光是显然的；三是平滑性，即不能有突变，这就要求函数的定义域包括整个导光板。这就可以大致知道试探函数应该是中间大边缘小的左右对称的钟形曲线。我们在此联想到，在数理统计理论中，如果一个量是由许多小的独立随机因素影响的结果，那么就可以认为这个量具有高斯分布函数的性质，而高斯函数正是上面所说的左右对称的钟形曲线，这就自然想到有很多个网点的随机散射的导光板的网点分布具有高斯函数的性质。这里要说明，虽然每条光线的散射方向是独立随机的，但我们却不能严格证明网点半径分布是符合高斯分布的。不过本文不去证明网点半径分布是高斯分布，而是假定网点分布符合高斯分布，反过来看这种网点分布是否能够给出均匀的照度分布？其答案是能。

下面从高斯分布函数出发，再由矩形导光板的边条件求得网点半径分布函数。

高斯函数的标准形式为

将此函数用在导光板网点半径分布时，其系数的意义就应该是中心点的半径，令其为r1。将此式略加改型,即

(14)

式(14)中w是表示分布宽度的一个量，其系数为r1表示导光板中心点的网点半径。而原来的指数2改成了变量ax，其目的是可以在2附近的一个小范围内变化，以便在保持高斯函数性质的前提下人工地略微改变函数的分布，从而达到高均匀度。为了使函数仍然左右对称，必须把x变为│x│。

令导光板边缘的半径为r2，则求解方程

(15)

可得w的符号解为

(16)

把式(16)代入式(14)，并把函数的形式改为多元函数，就得到了对边进光时的x方向网点半径rx的分布函数的符号形式为

(17)

举一个例子，半边长为50的导光板，其中心和边缘网点半径分别为0.3和0.02，半径分布就应该简洁地表示为

rx(x,0.3,0.02,50,2)=

(18)

作图可得图2。

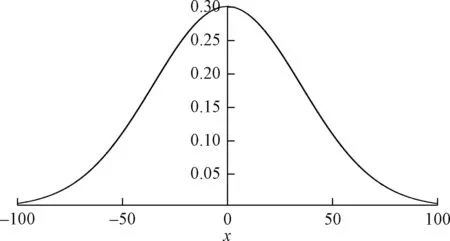
图2 对边进光导光板网点半径分布函数举例Fig.2 The dot radius distribution of light guide plate with bilateral edge lighting

对于一个给定长度Lx的导光板，令ax=2，只要调节r1和r2的大小，用式(17)比较容易满足均匀分布的要求，还可以略微调节ax来微调亮度分布。

3 四边进光网点半径分布函数

设矩形导光板两个方向的半长度为Lx和Ly，可以直接把式(17)推广到y方向，立刻可以写出y方向网点半径分布函数为

(19)

这里x和y是独立的，在数学上是可以分离的变量，因此总的函数可以写为

(20)

举一个例子，矩形导光板长度为1 000 mm×600 mm，中心和边缘网点半径为0.5和0.1 mm，代入式(20)，得到网点半径的分布函数表示为rxy(x,y,0.5,0.1,2,500,300)，计算此函数并作图如图3所示。

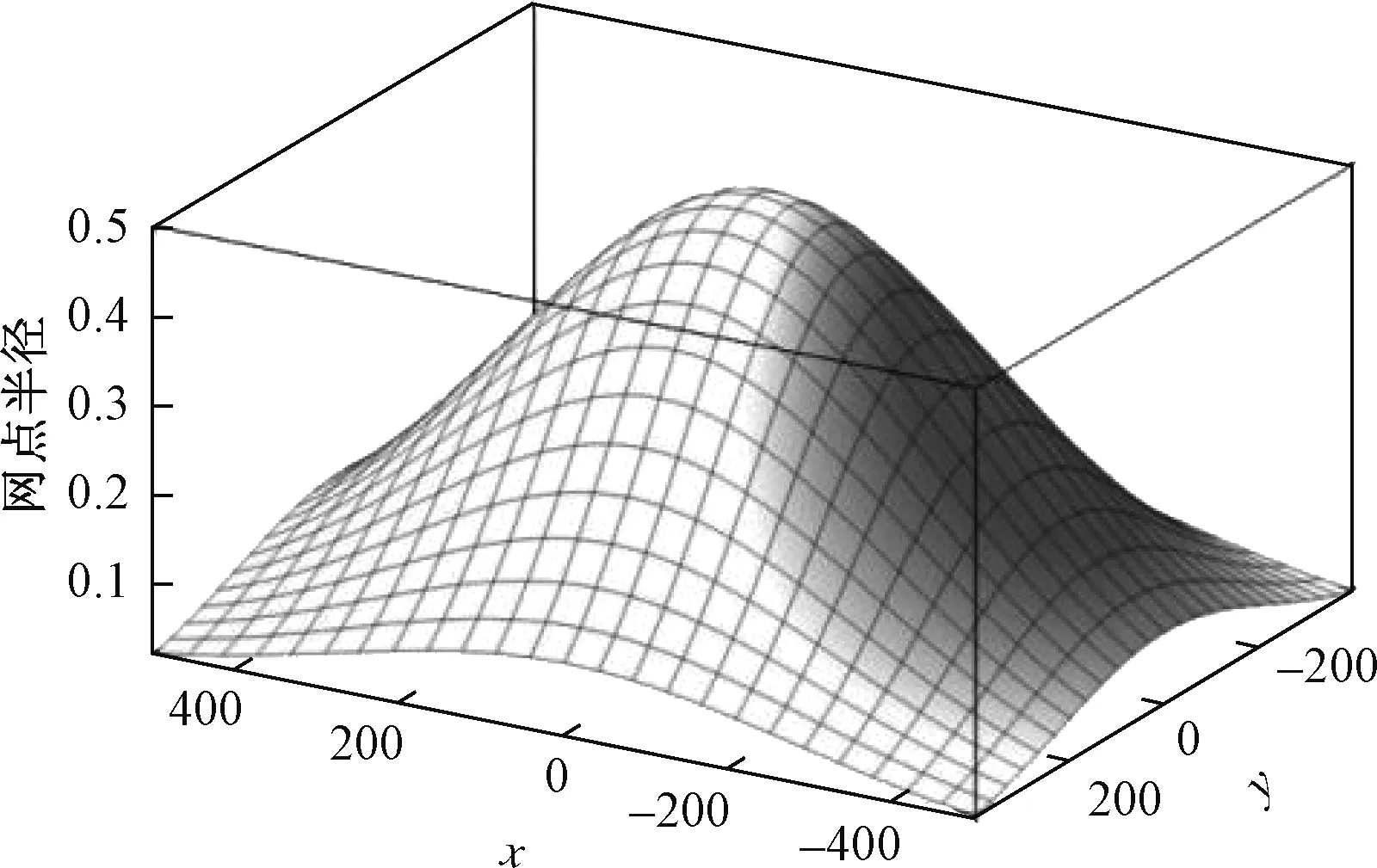
图3 四边进光导光板网点半径分布函数举例Fig.3 The dot radius distribution of light guide plate with quadrilateral edge lighting

4 网点半径分布表

现在，求网点分布的问题就变成有了函数求自变量各个值时的函数值的简单问题。可以先列出一个以x,y,r三个变量为三列的空表。网格的间距是可以根据工艺水平等因素选择，后面的例子中都是针对圆形网点和正方形网格。

以对边进光为例，网点计算结果见图4所示。这里为了读者看清规律，计算的网点数目比实际结果小了100倍。

图4 对边进光导光板网点原理图Fig.4 Principle map of the dot-pattern of light guide plate with bilateral edge lighting

实际上网格的形状可以为正方形、长方形、三角形或多边形，由于这些形状的规律性很强，用简单的程序就可以解决此问题，这就不难在各种网格形状下填充半径分布表中的所有x和y值。

得到网点半径分布表以后，还可用商用仿真程序如TracePro或LightTools进行仿真，这当然还要把上述分布表简单地变成符合你使用的仿真程序具体格式要求的表格，这里也不必细说。

5 网点分布的局域随机化方法

规则的网点分布有可能会产生莫尔条纹[18],从而影响导光板的均匀性。在网点间距较大时，可以用进一步优化网点分布的方法改善均匀性。优化网点分布的理论工作比较多[6-19]，如斥力缓和法、动态分子法、超均匀分布理论等。其中较先进的方法是动态分子法，这种方法可以理解为把网点看成一个个气体分子，按分子动力学的理论，网点就像气体分子那样，距离远了则引力起主要作用，将其拉近，距离近了则斥力起主要作用，则将其推远，最后达到平衡时的距离，同时也达到一个随机分布。但动态分子法循环周期长，耗时多。而且有人还对等半径的网点做过试验[16]，用动态分子法做无数次循环，最终结果反倒是所有分子(网点)都达到了平衡状态，结果造成一个事与愿违的均匀网点分布。总之，由于这些工作的复杂性高，因此实用性较低，大都还是停留在理论层面上。

我们使用的方法称为局域随机化的方法，是一个非常简单可靠的方法，就是用数学上的随机函数产生一个随机数，让网点在局部范围内抖动一个有限的距离。实际结果证明这种简单的的方法也完全可以满足随机化的要求。我们尝试了多个随机化的方法，最终采取的方法是分别对网点的x和y坐标在周围没有被网点占用的范围内随机性移动一个距离，逐个对所有网点进行这个操作，就得到了新的网点分布。

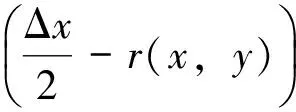
(21)

这样，对每个(x,y)都进行相同的操作，就会得到抖动后的网点分布。这一过程在求网点分布表的程序中只要增加很小的一段程序就可以完成。而且用局域随机化方法得到的新的网点基本上不会与附近的网点重叠。

由于抖动的距离比起导光板尺寸来说非常小，而半径分布函数是一个缓变函数，即函数值随位置的变化不大，可以只抖动改变x和y的值而不改变r值。因此它也可以在得到网点分布表以后进行。

采用本文的局域随机化方法对图4的结果进行处理，结果见图5。

图5 网点随机化原理Fig.5 Dot randomization principle

6 导光板仿真和实测

为了得到出光表面均匀的照度，在给定网格间距后要按照度仿真结果调整r1和r2。好在本方法需要调整的变量很少，而且实践证明很快就可以得到满意的结果，可以参照文献[12]的方法进行调整。

以上看起来相对简单的公式能够得到均匀出光的导光板吗？首先是用商用软件进行仿真来证明。

6.1 单边进光导光板仿真

举例，导光板尺寸为100 mm×60 mm,坐标原点在正中心，点间距采用1.5 mm，用式(13)计算网点半径。仿真的结果表明，当r1=0.3,r2=0.37时导光板亮度均匀度可以得到较好的结果。此时的半径分布函数为r(x,0.3,0.37,50)，整个导光板的半径分布函数如图6所示。

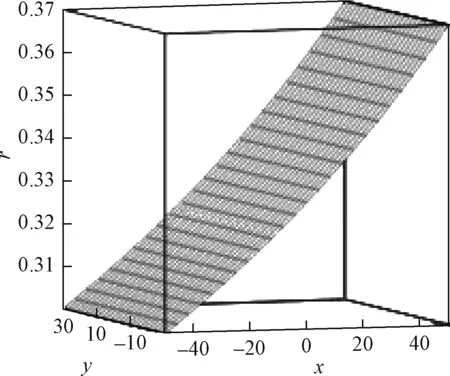
图6 单边进光导光板网点半径分布函数Fig.6 The dot radius distribution function of light guide plate with unilaternal edge lighting

在98 mm×58 mm的范围内计算可得2 680个网点，用第5节的方法进行随机化运算，结果见图7所示。

图7 单边进光100 mm×60 mm导光板网点图Fig.7 Dot map of 100 mm×60 mm light guide plate with unilaternal edge lighting

在TracePro中仿真的导光板表面照度分布,所用光线数为700 000，结果见图8。

6.2 对边进光导光板仿真

对于对边进光的情况，我们以发光天花板用的平板灯为实际目标，计算了一个边长为为270 mm，正方形网格的导光板，点间距Δx=Δy=1.4 mm，用式(17)计算网点半径。

图8 单边进光导光板照度分布仿真结果Fig.8 Illuminance simulation result of the light guide plate with unilaternal edge lighting

仿真的结果表明，当中心网点r1=0.31 mm，边缘网点r2=0.14 mm，而ax=2时导光板亮度均匀度就可以得到较好的结果,此时半径分布函数为rx(x,0.31,0.14,135,2)，整个导光板的半径分布函数如图9所示。

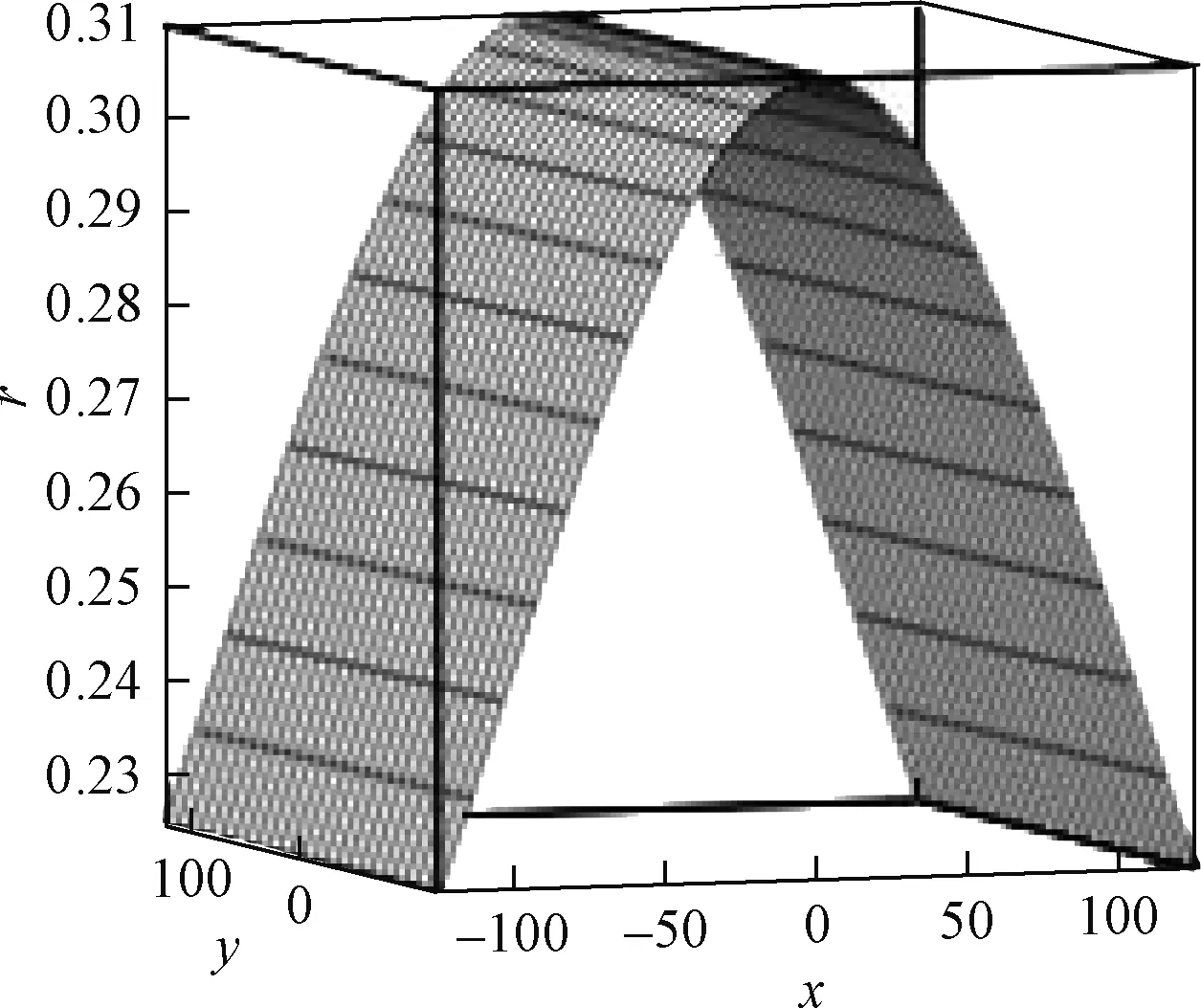
图9 双边进光导光板网点半径分布函数Fig.9 Dot radius distribution function of the light guide plate with bilateral edge lighting

图10 对边进光270 mm×270 mm导光板网点图Fig.10 Dot map of 270 mm×270 mm light guide plate with bilateral edge lighting

在268 mm×268 mm范围内的网点总数为32 014个，采用局域随机化方法优化计，图10为计算结果。图11为在TracePro中仿真的导光板表面照度分布。

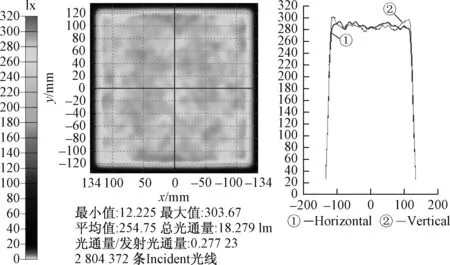
图11 对边进光导光板照度分布仿真结果Fig.11 Illuminance simulaton result of the light guide plate with bilateral edge lighting

仿真结果是在未经区域性修正情况下得到的，均匀度达到了97%，这也说明本文的方法是较成功的。

6.3 四边进光导光板仿真

四边进光可以用于相对较大的导光板，但此时要达到较好的均匀性就更困难，用本文的式(20)却可以较好地解决此问题。以1 000 mm×1 000 mm的正方形导光板为例。这里直接给出其网点半径分布函数、22万个圆形网点分布、仿真亮度分布等结果分别见图12、图13和图14所示，不再详细说明。

6.4 对边进光导光板制造和测量

我们用6.2节计算结果制作了270 mm×270 mm对边进光的导光板，网点为圆形，黑色油墨印刷，分别使用PMMA和钢化玻璃两种材料进行试制，并组装成300 mm×300 mm的平板灯，可以用在发光天花板等地方。图15为我们试制的平板灯灯具。

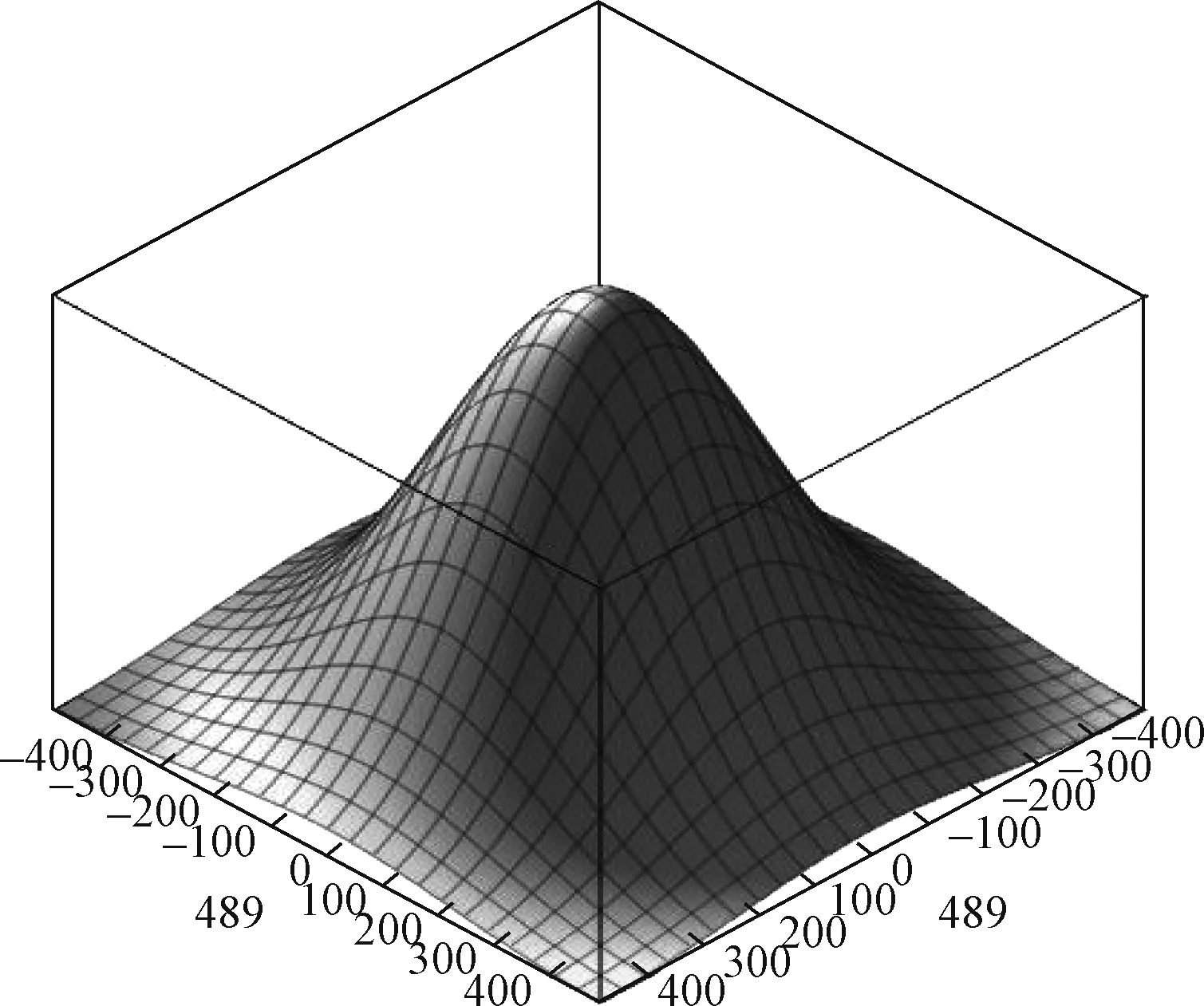
图12 四边进光导光板网点半径分布函数Fig.12 Dot radius distribution function of the light guide plate with quadrilateral edge lighting

图13 四边进光1 000 mm×1 000 mm导光板网点图Fig.13 Dot map of 1 000 mm×1 000 mm light guide plate with quadrilateral edge lighting

图14 四边进光导光板照度分布仿真结果Fig.14 Illuminance simulation result of light guide plate with quadrilateral edge lighting

图15 侧发光导光板组装的面光源平板灯Fig.15 The panel lamp with plance light source assembled by the light guide plate with edge lighting

该样品实际加工后测量的表面照度均匀度如表1所示，均匀度为92.1%，与仿真结果有差别，分析主要是由于仿真是按照材料吸收为零进行的。表面亮度正比于照度。

经验证明，矩形导光板边缘的四个角容易和中间的照度不同，而令人高兴的是，在我们加工的例子中，没有发生这种情况，一轮计算就得到了很好的均匀度。在其他情况下，如果出现了不均匀的情况，或需要更高的均匀度，则还可以进行局部调整，也就是对某些位置的网点修改其r值。我们已经给出了具体的局部调整的计算方法和程序，但不在本文中给出，只需说明基于网点半径分布表，只要判断x，y是否在修改的范围内就可以用计算机辅助来进行修正了。

表1 面光源平板灯表面照度实测结果

7 讨论

1)本文对光源的性质没有要求，冷阴极荧光灯(CCFL)或发光二极管(LED)都可以用。对网格的形状也没有要求。本文的公式是以印刷式圆形网点为对象，而对于非圆形或非印刷式网点则根据情况对式(5)略加修改。

2)本文的公式是基于连续函数得到的，公式中没有网点间距这个自变量，这意味着我们的实用函数实际上适用于任何网点间距。但实际上太大的间距会违反统计分布原理，而且导致网点半径太大使得均匀度降低，太小的间距会导致半径太小而不利与加工。

3)本文的公式是针对圆形网点的。但对其他形状的印刷式网点，只要所有网点形状都一样，则决定网点面积的仍然是单个长度量，只需要把r改为另一个长度量即可。而对单边进光的情况要根据简单的几何关系修改式(5)。

4)商用软件TracePro 2013年以后的版本有一个插件，其中采用了高斯函数来作为“占空比”的分布函数。但它只能用于旋转对称的分布，因此它并不适合矩形导光板，特别是对边进光的情况。而且其高斯函数的具体形式不能变，也就是调节分布时只能函数的中心值和边缘值两个点。因此不能得到令人十分满意的结果。

5)用多项式代替高斯函数也是可能的，但前者有明显的缺点，那就是参数太多，使用不便。

[1] 黄碧云，林志贤，陈恩果，等.侧入式LED背光模组中光耦合模块的设计与实现.光学学报，2016，36(2)：195.

[2] 张启，高慧芳，李忠良，等.提高侧背光液晶显示器光效的方法.光电子技术，2017，37(1)：44.

[3] 高双红，杨俊逸，王蕾，等.用于照明的侧光式导光板网点设计[J].照明工程学报，2012,23(6):103-105.

[4] 林晓新，项颖，庞晓峰.侧入式LED背光源导光板网点设计与仿真[J].广东工业大学学报，2014，41(4)：95-99.

[5] 骆健忠，陈哲，张永林，等，侧光平板式导光板散射网点设计及仿真分析[J].液晶与显示，2006,21(3)：206-212.

[6] 智佳军，梁铭泉，陈俄振，等. LED单边侧入式导光板的网点设计[J].照明工程学报，2012,23(3):60-63.

[7] 纪玲玲，王洪，张威，等. 一种导光板网点分布的计算方法与仿真[J].现代显示, 2010,113: 38-41.

[8] 黄翀，姜言森，沈奕，等. 侧光式LED背光源的导光板网点设计[J].应用光学，2008，29(5)：690-692.

[9] 康敏武，郭康贤，刘佐濂，等.实现导光板网点合理性分布的研究[J]. 广州大学学报，2010，9(2):26-31.

[10] 庞晓峰.导光板网点设计与优化.光电·材料，2015，28(11)：67.

[11] 黄逸峰，李潇，高培丽，等.侧入式导光板网点全自动优化设计研究.发光学板，2016，37(6)：751.

[12] 黄炳乐，郭太良，陈思果，等.导光板网点平均密度范围的最优化研究.光学学报，2015，35(5)：306.

[13] CHANG JG, SU MH, LEE CT, et al. Generating random and no overlapping dot patterns for liquid-crystal display backlight light guides using molecular-dynamics method[J]. J App. Phy., 2005,98(11):114910.1-114910.8

[14] IDÉ T, MIZUTA H, NUMATA H, et al. Dot pattern generation technique using molecular dynamics[J]. J. Opt. Soc., 2003,20(2):248-255.

[15] 臧金浩,侯瑶.侧入式LED导光板结构的设计与优化[D].西安：西北大学, 2008.

[16] 赵星星.导光板网点随机分布和矢量性研究[D].北京：北京交通大学，2008.

[17] 史永胜,魏文君，王秀峰.基于TracePro软件的LCD导光板网点分布仿真与研究[J].液晶与显示, 2007,22(4):463-466.

[18] LAU D L, KHAN A M, AREE G R. Proceedings of the 2001 Imaging Processing, Image Quality, Image Capture Systems Conference[C]. Society for Imaging Science and Technology, Springfield, Va. 2001.

[19] 王大巍，王刚，李俊峰，等. 薄膜晶体管液晶显示器件的制造[M]. 北京：机械工业出版社，2007.

Dot Radius Distribution Function and Dot-pattern Design of Light Guide Plate with Edge Lighting

ZHOU Shikang, ZHOU Junwei, DU Jin, CHEN Chungen

(ShanghaiSansiTechnologyCo.Ltd,Shanghai201100,China)

The dot radius distribution functions of light guide plate with edge lighting are derived in this paper for unilateral, bilateral and quadrilateral edge lighting. The function with unilateral lighting is derived based directly on the basic principle of light guide plate, while the functions with bilateral and quadrilateral edge lighting are the solutions of the modified Gaussian distribution function under the boundary value conditions of the plate. The functions, with the variables having definite physical meaning such as length of the light guide plate and the radius of the bordered and central dots, can be directly used for the design of rectangle light guide plate with different size. In order to further optimize the luminance uniformity of the light guide plate, a kind of very simple optimizing method called "local area randomization method" are proposed. The simulation results for three types of edge lighting and the measure results of actual manufacture lamps for bilateral edge lighting as an example have very good luminance uniformity. It is shown that the above method is a successful design method for light guide plate.

LGP; edge lighting; scattering netted dots; dot-pattern design; LED; lighting

O43 TN312

A

10.3969/j.issn.1004-440X.2017.04.020