吸气式高超声速飞行器反演自适应控制

贾二勇， 袁 涛， 王鹏飞， 何 维

(68206部队， 甘肃 临夏 731800)

吸气式高超声速飞行器反演自适应控制

贾二勇， 袁 涛， 王鹏飞， 何 维

(68206部队， 甘肃 临夏 731800)

针对吸气式高超声速飞行器纵向平面控制问题， 提出一种反演自适应控制设计方法。 将飞行器结构的弹性振动转化为运动方程中的不确定项， 基于反演控制思想分别设计了速度和高度控制器。 通过对模型中不确定项的上界进行自适应估计， 消除弹性振动对控制系统的影响。 引入滑模微分器对虚拟导数进行求解， 避免出现传统反演控制中的虚拟导数计算量膨胀问题。 仿真结果表明， 所设计控制器能够在模型存在不确定的情况下实现对速度和高度参考输入的高精度稳定跟踪。

吸气式高超声速飞行器; 反演控制; 自适应控制; 弹性振动; 滑模微分器

0 引 言

吸气式高超声速飞行器(Air-Breathing Hypersonic Vehicle, AHV)是指飞行在临近空间， 以超燃冲压发动机为动力， 飞行马赫数大于5的一类新型飞行器。 在军事领域， 其作为一种新的高空高速突防打击利器， 必将在未来空天一体化战争中起到首当其冲的作用； 在民用领域， 可开发能够重复使用的空天往返飞行器， 大大降低空天探测成本， 为民用航天运载提供全新途径。

相比传统飞行器， AHV大量使用轻薄材料， 且多采用乘波体构型， 因此AHV在气动/结构/推进之间存在严重的耦合效应， 导致其动力学特性呈现显著的非线性和非最小相位行为[1]， 传统的控制方法难以满足AHV飞行控制需求。 目前， AHV的飞行控制系统设计问题已成为控制科学领域的前沿问题之一。

由于反演设计方法在处理非匹配不确定性方面的独特优势， 现已成为AHV控制系统设计的主流方法之一[2-7]。 文献[8]提出一种指令滤波反演控制方法， 并结合动态逆策略设计了动态状态反馈控制器， 该控制器解决了传统反演控制中存在的“微分项”膨胀问题。 文献[9]在反演设计框架下， 针对模型中存在的不确定扰动， 设计了一种自适应干扰估计算法， 有效地提高了干扰估计的准确性。

如何抑制AHV模型中的弹性振动是控制系统设计必须解决的难题。 由于弹性振动无法直接测量， 因此难以直接应用于控制器的设计。 目前， 通常的做法是将弹性振动视为未知扰动， 通过控制系统的鲁棒性来抵消其对控制稳定性的影响。 因此， 如何处理模型中的不确定项， 提升控制器的鲁棒性， 成为设计控制器中必须考虑的问题。

本文首先从反演设计方法对模型的需求出发， 基于AHV的纵向平面动力学原理模型， 通过对模型中的各种作用力进行多项式拟合， 形成适合反演设计方法的仿射控制模型， 然后针对如何提高控制系统鲁棒性这一设计目标， 基于反演设计方法开展吸气式高超声速飞行器飞行控制系统的设计。 为降低弹性振动对控制器的影响， 将振动对刚体状态的影响转化为有上界不确定干扰问题， 通过设计自适应估计策略， 对未知扰动实现自适应估计。 区别于传统的动态面法， 文中引入滑模微分器对虚拟控制量的导数进行求解， 避免反演控制中虚拟导数计算量膨胀的问题。 最后， 通过相关的轨迹跟踪仿真实例对控制器的有效性进行了检验。

1 系统建模

定义飞行器刚体动力学系统状态量x=[V,h,γ,θ,Q]T。 其中：V和h分别为飞行速度和高度；γ和θ分别为航迹角和俯仰角；Q为俯仰角速率；θ=γ+α，α为飞行攻角。 飞行器的动力学方程为[10]

(1)

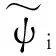
基于曲线拟合的思想， 将推力、 气动力和力矩表示为虚拟控制量和控制量的非严格仿射形式[10]：

(2)

其中：

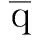
为方便后续控制器设计， 将式(1)转换为下述形式：

(3)

式中：

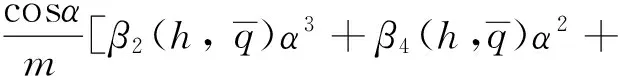
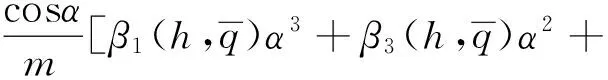
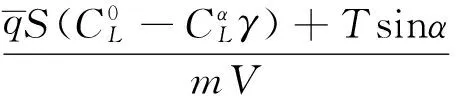
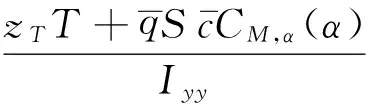
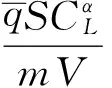
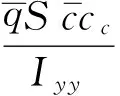
其中：dV,dγ和dQ均为模型的不确定项。

从式(3)可以看出， 速度V主要由燃料当量比Φ所控制， 而高度h主要受升降舵偏角δe的影响。 因此， 通常在形式上将速度控制器和高度控制器分开设计， 分别设计Φ和δe的控制律实现V→Vref和h→href， 即实现速度和高度对各自参考轨迹Vref和href的稳定跟踪。

2 控制系统设计及其稳定性判定

为便于后续控制系统分析， 做如下假设：

2.1 速度控制器设计

定义速度相关子系统的跟踪误差：

(4)

对其求导得

(5)

选取控制量Φ为

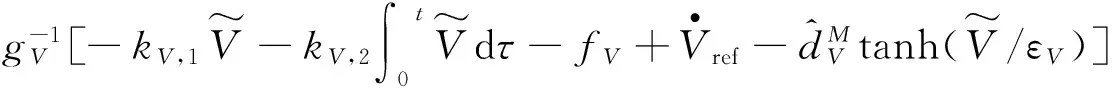
(6)

式中：kV,1，kV,2为待设计的正参数；εV>0为待设计的常数。

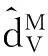
(7)

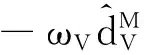
2.2 高度控制器设计

选取干扰项上界的估计误差为

(8)

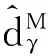
定义高度的跟踪误差为

(9)

选取控制律为

(10)

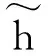
定义航迹角的跟踪误差为

(11)

则有

(12)

选取虚拟控制量为

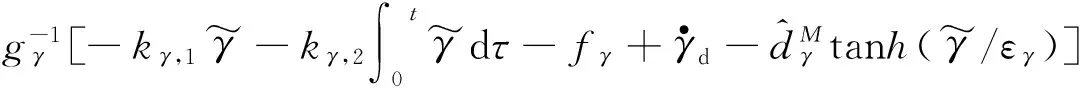
(13)

式中：kγ,1和kγ,2均为大于0的设计参数。

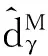
(14)

式中：σγ>0和ωγ>0为设计参数。

为避免虚拟导数计算膨胀问题， 引入一阶滑模微分器[12]对θc的一阶导数进行精确估计：

(15)

式中：λ11和λ12为待设计参数。

定义俯仰角的跟踪误差为

(16)

对上式求导得

(17)

虚拟控制量Qc定义为

(18)

其中:kθ,1,kθ,2均为正的待设计参数。

同样, 对Qc的导数进行估计可得

(19)

式中：λ21和λ22为待设计的正参数。

定义俯仰角速率的跟踪误差为

(20)

则有

(21)

选取实际输入δec为

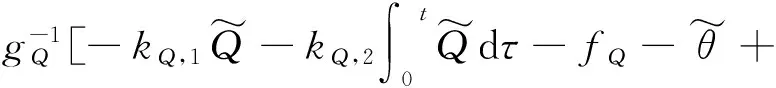
(22)

式中：kQ,1和kQ,2为正的控制器参数。

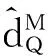
(23)

式中:σQ>0和ωQ>0为设计参数。

2.3 稳定性分析

为便于后续证明， 首先给入下述引理：

引理1： 对于任意的y∈R和任意常数ε>0， 有下列不等式的关系成立[11]：

0≤|y|-ytanh(y/ε)≤κε

(24)

其中：κ≈0.278 5。

定义虚拟控制量的估计误差为

(25)

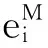
选取Lyapunov函数：

W=WV+Wγ+Wθ+WQ

(26)

式中：

(27)

(28)

(29)

(30)

分别对式(27)～(30)进行求导得

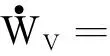
(31)

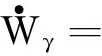
(32)

(33)

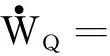
(34)

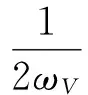
(35)

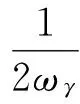
(36)

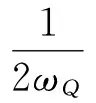
(37)

式中：κV，κγ和κQ均为引理1中的常数。

由于：

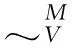
(38)

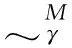
(39)

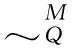
(40)

则式(26)可以改写为

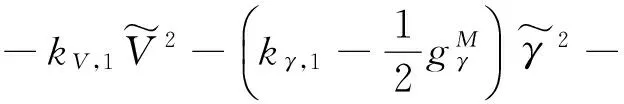
(41)

式中：

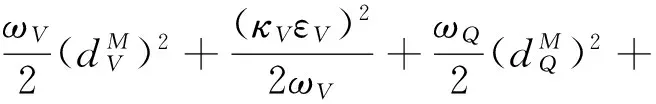
定义如下紧集：

(42)

(43)

(44)

(45)

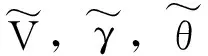
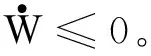
3 仿真分析

针对吸气式高超声速飞行器纵向动力学模型进行闭环系统仿真， 模型的参数及标称气动力、 气动力矩系数见文献[10]。 飞行器的初始条件：初始高度为25 908 m， 初始速度为2 347.58 m/s。 保持速度不变， 高度跟踪幅值为182.88 m， 周期为200 s的方波信号， 将高度和速度分别利用自然频率为0.1 rad/s、 阻尼为0.9的二阶参考模型获得跟踪轨迹。

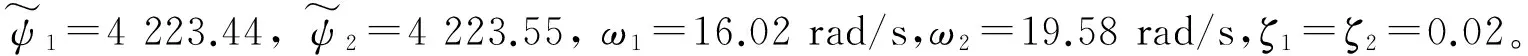
经过400 s的仿真时长， 结果如图1～6所示。 从图1～2中看出， 在控制器作用下， 速度和高度能够始终稳定跟踪给定的指令。 由于在仿真周期内高度的参考轨迹发生多次变化， 因此导致跟踪误差也出现了多次波动， 但是经过控制输入的短暂调整，能够保证跟踪误差迅速收敛至0； 图3表明， 控制输入只在高度指令切换时出现短暂抖振， 其余时刻都能够迅速收敛至平衡状态； 图4～5显示的是系统刚体状态量和弹性状态量的变化曲线， 可看出两者均能迅速趋近另一平衡状态， 虽然随高度指令的变化有所波动， 但是各状态量变化均处于各自的约束范围内。 图6所示为干扰上界的估计曲线， 可以看出控制系统对干扰的上界实现了较好的估计， 上界的变化处于合理范围内。

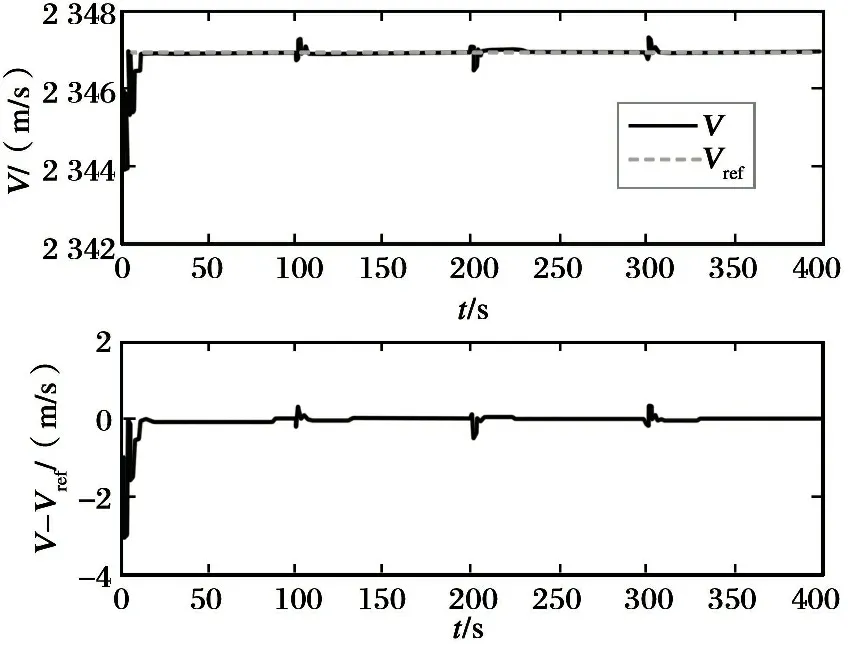
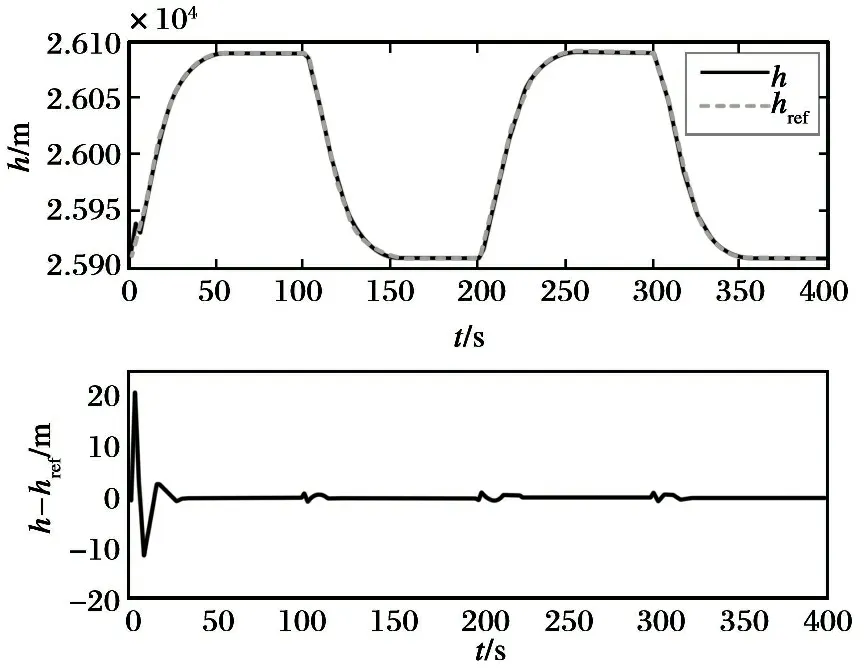
图1 速度跟踪曲线及跟踪误差曲线

图2 高度跟踪曲线及跟踪误差曲线

Fig. 2 Response curves of altitude and altitude tracking error

图3 控制量曲线

图4 航迹角、 俯仰角及俯仰角速率的响应曲线

Fig.4 Response curves of flight path angle, pitch angle and pitch rate

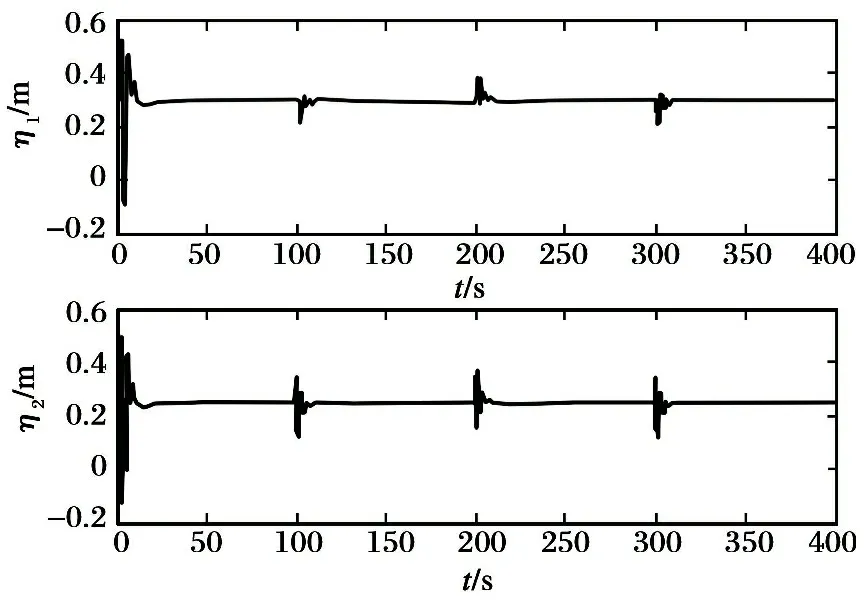
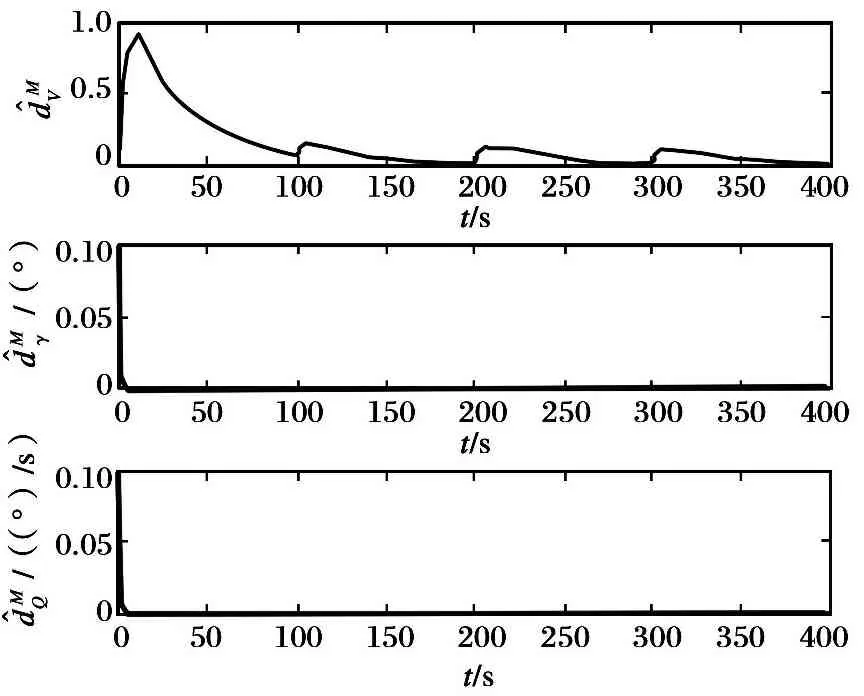
图5 弹性模态响应曲线

图6 干扰上界的估计

Fig.6 Estimation curves of disturbance’s upper bound

4 结 论

本文针对高超声速飞行器纵向平面的控制问题， 设计了一种反演自适应控制器。 将弹性状态对刚体状态的影响转化为有上界不确定干扰问题， 设计自适应估计律对未知干扰项进行估计。 为避免反演控制中虚拟导数计算量膨胀的问题， 引入滑模微分器对虚拟导数进行求解。 仿真结果表明， 所设计控制器在保证刚体状态稳定的同时， 能够较好地抑制机体弹性振动， 实现对速度和高度参考输入的高精度稳定跟踪。

[1] Hu Xiaoxiang, Wu Ligong, Hu Changhua, et al. Adaptive Sliding Mode Tracking Control for a Flexible Air-Breathing Hypersonic Vehicle[J]. Journal of the Franklin Institute, 2012, 349(2): 559-577.

[2] Gao Daoxiang, Sun Zengqi, Liu Jinhao. Dynamic Inversion Control for a Class of Pure-Feedback Systems[J]. Asian Journal of Control, 2012, 14(2): 605-611.

[3] Gao Daoxiang, Sun Zengqi, Xu Bin. Fuzzy Adaptive Control for Pure-Feedback System via Time Scale Separation[J]. International Journal of Control Automation Systems, 2013, 11(1): 147-158.

[4] 宗群， 吕力, 田栢苓， 等. 基于Backstepping的临近空间飞行器非线性控制[J].控制工程, 2012, 19(5): 860-863，869. Zong Qun, Lü Li, Tian Bailing, et al. NonlinearH∞Control for Near Space Vehicle via Backstepping Method[J]. Control Engineering of China, 2012, 19(5): 860-863, 869.(in Chinese)

[5] 黄喜元,王青,董朝阳. 基于Backstepping的高超声速飞行器鲁棒自适应控制[J]. 系统工程与电子技术, 2011, 33(6): 1321-1326. Huang Xiyuan, Wang Qing, Dong Chaoyang. Robust Adaptive Control of Hypersonic Vehicles via Backstepping Method [J]. Systems Engineering and Electronics, 2011, 33(6): 1321-1326.(in Chinese)

[6] 卜祥伟， 吴晓燕， 陈永兴， 等. 基于非线性干扰观测器的高超声速飞行器滑模反演控制[J]. 控制理论与应用, 2014, 31(11): 1473-1479. Bu Xiangwei, Wu Xiaoyan, Chen Yongxing, et al. Nonlinear-Disturbance-Observer-Based Sliding Mode Back-Stepping Control of Hypersonic Vehicles[J]. Control Theory & Applications, 2014, 31(11): 1473-1479.(in Chinese)

[7] Zong Qun, Ji Yuehui, Zeng Fanlin, et al. Output Feedback Back-Stepping Control for a Generic Hypersonic Vehicle via Small-Gain Theorem[J]. Aerospace Science and Technology, 2012, 23(1): 409-417.

[8] Ji Yuehui, Zong Qun, Zhou Hailiang. Command Filtered Back-Stepping Control of a Flexible Air-Breathing Hypersonic Flight Vehicle[J]. Journal of Aerospace Engineering, 2014, 228(9):1617-1626.

[9] 张强, 吴庆宪, 姜长生, 等. 基于Backstepping的近空间飞行器鲁棒自适应姿态控制[J]. 南京航空航天大学学报, 2013, 45(5): 590-598. Zhang Qiang, Wu Qingxian, Jiang Changsheng, et al. Robust Adaptive Control for Attitude System of Near Space Vehicle via Backstepping Method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(5): 590-598.(in Chinese)

[10] Parker J T, Serrani A, Yurkovich S, et al. Control-Oriented Modeling of an Air-Breathing Hypersonic Vehicle[J]. Journal of Guidance, Control and Dynamic, 2007, 33(3): 856-869.

[11] Xu Bin, Huang Xiyuan, Wang Danwei, et al. Dynamic Surface Control of Constrained Hypersonic Flight Models with Parameter Estimation and Actuator Compensation[J]. Asian Journal of Control, 2014, 16(1): 162-174.

[12] Levant A. Higher-Order Sliding Modes: Differentiation and Output Feedback Control[J]. International Journal of Control, 2003, 76(9): 924-941.

AdaptiveBack-SteppingControllerDesignforAir-BreathingHypersonicVehicle

JiaEryong,YuanTao,WangPengfei,HeWei

(Unit68206ofPLA,Linxia731800,China)

An adaptive back-stepping controller is designed for the longitudinal plane control problem of air-breathing hypersonic vehicles. The elastic vibration of aircraft structures is perceived as disturbance motion model. Based on back-stepping control method, velocity and altitude controllers are designed. The upper bound of the uncertainty in the model is adaptively estimated to eliminate the influence of the elastic vibration on the control system.The sliding mode differentiators are introduced to obtain the derivatives of virtual control laws, which avoids the explosion of virtual derivative calculation in the conventional back-stepping control. Reference trajectory tracking simulation shows that the effectiveness of this controller in tracking velocity and altitude commands in the presence of model uncertainty.

air-breathing hypersonic vehicle; back-stepping control; adaptive control; elastic vibration; sliding mode differentiator

10.19297/j.cnki.41-1228/tj.2017.04.003

2017-03-06

国家自然科学基金项目(61603410)

贾二勇(1980-)， 男， 陕西延安人， 硕士， 研究方向为飞行器控制。

贾二勇， 袁涛， 王鹏飞， 等. 吸气式高超声速飞行器反演自适应控制[ J]. 航空兵器， 2017( 4)： 14-20. Jia Eryong, Yuan Tao, Wang Pengfei, et al. Adaptive Back-Stepping Controller Design for Air-Breathing Hypersonic Vehicle[ J]. Aero Weaponry, 2017( 4): 14-20. ( in Chinese)

TJ765

： A

： 1673-5048(2017)04-0014-07