Delta动态对冲策略的模拟检验及实证研究

谢博文 辽宁大学经济学院

Delta动态对冲策略的模拟检验及实证研究

谢博文 辽宁大学经济学院

本文运用Excel及加载宏Crystal Ball软件进行蒙特卡洛模拟，对普通时点对冲，Leland策略，固定区间对冲和Whalley-Wilmott策略进行比较分析，得出Leland策略优于普通时点，Whalley-Wilmott策略优于固定区间对冲的结论，并进一步研究了Whalley-Wilmott策略有效容忍区间的选择。最后使用招行股票进行实证分析。

蒙特卡罗模拟 delta对冲 策略比较 Whalley-Wilmott策略容忍区间

一、前言

作为风险管理的工具，delta对冲广泛运用于投资基金的组合管理。delta是衍生品价格C相对于标的资产价格S的变化率，描述的是两者价格关系的斜率，公式表示为：

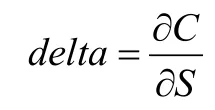
delta对冲就是通过资产组合的构建，使整个组合的各个部分的delta相互抵消，达到delta中性状态，也就是整个组合的delta为0，从而达到对冲保值的效果。下面说明其原理。

设S为股票价格，C为欧式看涨期权价格。假设S满足几何布朗运动，则

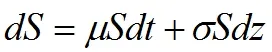
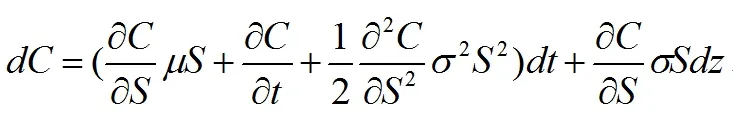
上面两式的离散形式为

ΔC 和ΔS 是在短时间Δt内的变化量。

构建一个资产组合：一个单位的欧式看涨期权的空头头寸和x单位的股票多头头寸。

该资产组合的价值

将（1）和（2）代入到（3）中，整理得

随着时间的变化，股票价格S会不断变化，看涨期权C的delta也会不断发生变化，所以要不断改变该资产组合中的股票数量，称为再平衡过程。这就是delta动态对冲的基本原理。对冲该看涨期权空头的策略可以看做以股票交易的形式来构造看涨期权的多头。

二、delta对冲策略的种类

delta对冲的实际效果是由标的资产价格的变动路径和再平衡的调整频率决定的。标的资产价格和时间的变化都会改变delta，所以在实践中，根据采用的delta策略的不同，要按照相关策略的标准，进行再平衡调整。主要策略有两类，固定时点和固定区间。

（一）固定时点对冲

固定时点对冲是指，首先确定好时间间隔，在每个时段末，进行交易，以保证资产组合整体delta为0。1985年，由Leland首次提出考虑比例交易成本的对冲模型，通过对波动率的修正改善对冲效果。调整后的波动率为

（k为比例交易成本的系数）使期权价格的增加与再平衡调整过程带来的交易成本相互抵消，进一步修正了B-S模型。

我们将基于B-S模型的策略称为普通时点策略，基于LELAND调整的策略称为leland策略。

（二）固定区间对冲

固定区间对冲是指，我们先计算资产组合的delta值，然后确定一个能容忍的delta变动的固定区间。资产组合的delta值变动时，只要变动值不超出，我们就不进行任何操作，一旦超出区间范围了，则进行调整。调整的方式有两种：第一种是调整至delta中性状态，即资产组合delta为0；第二种是将delta调整至容忍区间的边界，使delta值重新回到容忍区间，即[-d,+d]范围内。对于第二种策略，1997年，Whalley和Wilmott得到了delta对冲的无交易区间，其边界的表达式为

我们将第一种称为固定区间对冲，第二种称为Whalley-Wilmott策略。

三、Delta对冲的蒙特卡罗模拟检验

使用几何布朗运动的离散时间模型模拟股票价格变动过程，对四种策略进行模拟检验，模拟次数为10000次，每个价格变动路径包括90个时点的数据。分析方法运用经典的均值方差分析，计算每种策略的对冲成本期望值和标准差。

假设某金融机构卖出一份10000股无股息股票的欧式看涨期权。股票当前价格为49，收益率期望为13%，波动率为年20%，比例交易费用为0.005，无风险利率为年5%，期权执行价格为50，期权期限为90天，行权时按现金结算方式。现在对冲其看涨期权空头的风险，即运用delte对冲的原理合成看涨期权。

（一）四种策略的模拟结果

策略 期望 标准差普通时点对冲 26740.77 3464.28 LELAND模型 25629.13 2138.20区间对冲 25004.02 3450.83 W-W策略 22819.43 3042.99不采取任何策略 22901.79 33014.53

普通时点对冲和LELAND策略的对冲频率为每日一次。区间对冲和Whalley-Wilmott策略的容忍区间取为0.04，我们直观感觉为，容忍区间不应该太小，再平衡调整太频繁，交易成本大；太大，风险又过大，将于下一小节说明容忍区间的有效取值。

我们可以看到，不采取任何对冲策略时，成本的期望值很小，但是其标准差极大。评判策略是否更优，就是指在相同的标准差下，期望值更小，或者在相同的期望值下，标准差更小。所以从表可知，最优策略为LELAND和W-W策略。

（二）Whalley-Wilmott对冲策略的有效容忍区间的研究

我们知道欧式看涨期权的delta大于0小于1，而容忍区间大小的选取一旦超过MAX(初始delta,1-初始delta)后，delta的变动就不可能超过该区间，不会再有交易了，所以其上限为MAX（初始delta,1-初始delta）。

波动率为0.2时，初始delta为0.4892，所以区间上限0.5108。使用crystal ball的决策表功能，将区间大小设为决策变量，最小值为0，最大值为0.52，间隔为0.01。另外为了更清晰的观察较小区间增加后的实际效果，又计算了区间取0.001和0.005的点。所得部分数据的表格和全体数据的散点图如下：

图中红点为LELAND策略的数据点，从图中可以得知，随着区间选取的增加，期望值不断减小，而方差先减小后增大。由图可得，本例有效区间的上限为0.52，实际应为MAX（初始delta,1-初始delta），下限为0.03，实际应为曲线最低点的所代表的区间大小。我们发现一个有趣的现象，在区间小于曲线最低点时，区间越大，即再平衡调整的次数越少时，其标准差却越小,这与我们的直观感受不同。但仔细分析，可以发现，本文考虑了交易费用，而且每次再平衡调整时股票价格不同，一般都是高买低卖，另外，股票价格的波动率不高，较小的区间，带来更为频繁的调整，使再平衡调整的稳定性作用降低了，所以出现了上图的现象。我们可以将波动率增至0.5和1时，再次进行观察。

波动率为0.5时，初始delta为0.5375，所以区间上限0.5375。使用crystal ball的决策表功能，将区间大小设为决策变量，最小值为0，最大值为0.54，间隔为0.01。另外为了更清晰地观察较小区间增加后的实际效果，又计算了区间取0.001和0.005的点。所得部分数据地表格和全体数据的散点图如下：

波动率为1时，初始delta为0.5927，所以区间上限0.5927。使用crystal ball的决策表功能，将区间大小设为决策变量，最小值为0，最大值为0.60，间隔为0.01。另外为了更清晰地观察较小区间增加后的实际效果，又计算了区间取0.001和0.005的点。所得部分数据的表格和全体数据的散点图如下：

区间大小 期望值 标准差0 105081.10 9444.68 0.01 103695.40 9741.01 0.02 102693.40 10460.85 0.03 102163.00 11580.13 0.04 101539.70 12851.53 0.05 101367.30 14392.18 0.10 99886.45 22452.37 0.20 98850.62 40735.21 0.30 98543.25 59679.36 0.40 98300.24 73692.60 0.50 98530.86 76559.17 0.60 97807.03 77863.83 leland 104922.90 9359.40

果然，波动率为0.5和1时，不再出现随着容忍区间的增加，标准差反而减小的现象。但是从上面三个图表可以看出，波动率增大后，大区间的数值点越来越发散，这是因为大区间的再平衡调整极少，而本文假设的期权期限又只有90天，模拟次数只有10000次，就会出现有的区间进行模拟时，出现需要调整的路径多，有的少，造成发散现象。但随着区间的增大，期望值减小，标准差增加的趋势还是很容易看出的。

由图可得，波动率较大时，有效区间上限为MAX（初始delta,1-初始delta），下限为LELAND调整点。波动率为1时的LELAND点由于数值较为接近区间点，所以图中不能明显看出，但从数值表也可以看出。

当然，实际根据风险偏好选择最优区间时，我们不会选择很大的区间，图中也可看出此时曲线近似垂直了（此时选择更大的区间，期望减少得很慢，而方差增加得很快），波动率较大时，区间选择也不会偏好靠近LELAND策略点的那一段（此时选择更小的区间，方差减小得很慢，而期望增加得很快）。由于本文只考虑主要的这四种策略的优劣，所以W-W策略有效容忍区间的选择只有与LELAND策略的联动分析。

四、实证分析

国内A股市场上的一些规模很大的公司，如招行，中石油，贵州茅台等，流通股本大，交易活跃，价格波动平稳，满足delta对冲策略交易的要求。所以本文选取招商银行这一在我国证券市场上具有代表性的大盘股进行delta对冲策略的实证分析。

实证部分数据使用的是招行股票2016年4月29日至2017年4月29日的一年期数据。无风险利率选取2016年4月29日的一年期SHIBOR，为3.0420%，股票价格波动率使用历史波动率，计算可得，为14.84%，比例交易成本为0.005。假设在2016年4月29日，某金融机构卖出一份10000股招行股票的欧式看涨期权，股票初始价格为17.75，执行价格为18，期限为1年。我们使用delta对冲策略合成该看涨期权多头来对冲风险。

实际delta对冲后的结果如下：

对冲策略 对冲成本普通时点 12915.78 LELAND策略 12745.52区间对冲 C=0.04 12309.05 W-W策略 C=0.04 11894.11 W-W策略 C=0.1 9689.30 W-W策略 C=0.2 6944.04不采取任何策略 11300.00

由于使用实际数据进行分析，所以只能体现出最终对冲成本的大小，风险大小无法直接观察到。因为股票最终价格为19.13，期权执行价格为18，所以不采取任何对冲策略时，金融机构的成本为11300。从本例可以看出，W-W策略的容忍区间越大，对冲成本越低，但实际上其标准差也会大很多，这在上一章的分析中已有所体现。这说明，由于交易费用的存在，当股票价格大致符合维纳过程时，再平衡调整频率的增加会使成本增大。实证结果基本符合上一章的分析。

五、结论

delta对冲策略是可行的，并且LELAND策略优于普通时点，W-W策略优于固定区间策略。W-W策略的区间越大，对冲成本越小，对冲风险越大，但是存在一个有效地区间，便于金融机构在不同的风险偏好下，选择合适的区间，另外，波动率的大小使容忍区间下限的选择也有所不同。

[1](加)赫尔著,（加）王勇,索吾林译.期权、期货及其他衍生产品[M].机械工业出版社,2016,1

[2]张程.期权动态风险对冲实证分析[J].现代管理科学，2010,第3期

[3]邹小芃.动态套期保值策略的模拟检验及在我国的应用[D].浙江大学，2002

[4]Leland, H., 1985, Option Pricing and Replication With Transaction Costs, Journal of Finance 40: 1283-1302

[5]Bill Dalton,2008,Financial Products-An Intruduction using Mathematics and Excel,Cambridge University Press

[6]Whalley, A. E. and Wilmott, P., 1997, An Asymptotic Analysis Of An Optimal Hedging Model For Option Pricing With Transaction Costs.Mathematical Finance,Vol.7,No.3