高职高数基本知识点的横向邻接与纵向拓展

戴兴波

摘 要：高等数学基本知识点，如果不注意学习技巧，不但在理解上会给学习者带来困惑，也会对记忆产生影响，从而会对后续衔接学习内容带来阻力。笔者通过多年的教学实践发现，高等数学的基本知识点在整体布局上是有规律可循的，有些知识点之间存在着有机的横向联系，有些知识点之间能够纵向相互支撑，也可以进行纵向拓展。

第一部分：基本知识点的横向邻接。我们以定积分为例。我们知道，定积分的概念是建立在极限基础上的，其基本思想是“化整为零、积零为整”或者叫“以曲代直”，以常规问题的解决手段解决非常规问题，如，不规则图形的面积、变速运动问题的即时速度等。从基本知识点的串接上，自然联想到了有限项加和公式各种极限的求法、原函数、不定积分、牛顿莱布尼茨公式等；从思想原理上来看，属于从特殊到一般然后再回到特殊中去的一种思维规律。从分析的过程不难看出，概念的横向串接往往是以类接和邻接为主，而纵向拓展也表现为纵深延拓和反向纵深延拓（即由深层次向浅层次追溯）。下面我们对类接和邻接进行专门总结。[1]

一、概念定理原理的类接

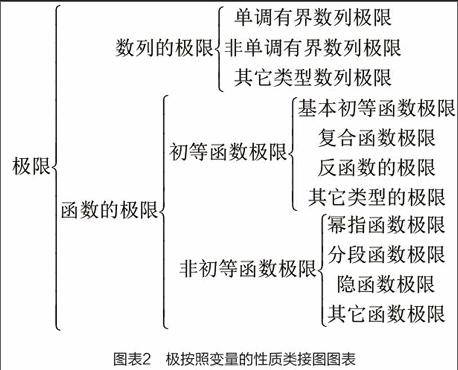
许多数学概念、定理、原理方面，都存在横向类接的问题。这类似于归类方面的知识链接，但又不完全等同于归类分析。同一个概念、原理、定理，如果从不同的角度，可以得到不同的类接结果。如极限的概念的类接如下图：

以上两种类接分析告诉我们，不同的分析角度可以产生两种完全不同的类接结果，这也就给我们提供了多层次类接分析的方法。通过本例我们得到了这样的启示：同样的概念、定理和原理，我们为了实现尽可能全面的了解，就要尽量从不同角度，对同样的问题进行多层次描述，从而达到全面分析掌握的目的。[2]

二、概念原理的邻接

许多数学概念、定理和原理之间存在着邻接。所谓邻接就是在概念层面上比较接近，在使用上能相互渗透，在记忆上能相互支撑的部分。[3]

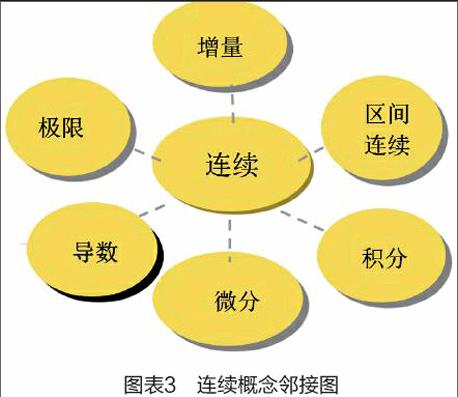
我们以连续的概念为例。连续，包括一元函数连续、二元函数连续、多元函数连续等。而连续本身的概念，就邻接着函数的定义域、函数值、奌极限等概念。另外，连续本身也类接着增量概念、导数、微分、积分、区间连续、最值性、有界性、介质性等都是连续的直接结果。因为连续是用增量定义的，而导数也是用增量进行定义的，只不过是，连续是关于自变量增量与函数增量的先后关联定义，而导数则是这两个增量的相互比值定义，而可微也是关于这两个增量变化的线性关系定义，从而存在着邻接关系。而连续函数一定存在原函数，从而也必然可积。如下所示：

第二部分基本知识点的横向拓展。高等数学的关键概念之间，不仅和其它概念之间存在着横向邻接联系，同时，还存着着纵向串接关系。再从纵向拓展和渗透的角度考虑，我们发现实际上是用简单的方法，解决了复杂的问题。例如：基本知识点的纵向拓展范例：极限—无穷小—导数---微分---积分

从定积分概念的纵向发展来看，从最初的一元函数的分割、取点、作和式、取极限定义过程，再到几何意义；从一元函数再到二元函数二重积分再到三重积分直至多重积分；从定积分再到可变上限的积分，从常规定积分再到反常积分（也称广义积分），如下图：

总之，数学的基本定理、基本概念、基本公式在知識点上存在着横向邻接关系和纵向串接拓展关系。正确的分析和处理这些关系，一方面能加深对概念的理解，另一方面，也能促进对概念本身记忆。也就是，虽然看上去这些概念之间似乎是孤立存在的，但实际上，他们之间存在着千丝万缕的联系，只要善于总结和发现这些关系，对如何学好高等数学，会带来意想不到的收获。

参考文献

[1] 周金才等，《数学的过去现在和未来》，中国青年出版社，1980年。

[2] 蒋术亮，《中国在数学上的贡献》，山西人民出版社，1984年。

[3]李迪，《中国数学史简编》，辽宁人民出版社，1984年。endprint