基于柯西矩阵的最小带宽再生码研究*

宋海龙，王伟平，肖亚龙

(1.中南大学 信息科学与工程学院，湖南 长沙 410083；2.吉首大学 信息科学与工程学院，湖南 吉首 416000)

基于柯西矩阵的最小带宽再生码研究*

宋海龙1,2†，王伟平2，肖亚龙1

(1.中南大学 信息科学与工程学院，湖南 长沙 410083；2.吉首大学 信息科学与工程学院，湖南 吉首 416000)

节点的失效在大规模分布式存储系统中是常见现象.为防止数据的丢失，系统必须解决失效节点的自修复问题.利用再生码可以在无需下载整个源文件的情况下即可恢复出失效节点的数据，从而能有效节省修复带宽.本文利用柯西矩阵作为编码矩阵，构造了一种精确修复最小带宽再生码(ER-MBR)，可以精确修复失效节点，并通过实例演示了在有限域上进行编码解码及节点修复的过程.理论分析和仿真实验都表明利用柯西矩阵作为编码矩阵，其算法的运算效率优于利用范德蒙矩阵或者随机矩阵.

纠删码；再生码；网络编码；柯西矩阵；范德蒙矩阵；分布式存储

近几年来，大规模数据存储的需求迅速增长.许多应用如社交网络、文件共享、流媒体点播、云存储系统等都要求对大规模数据的无缝存储、访问和安全保护.这些大规模数据都是通过分布式存储系统(如RAID-6[1]，OceanStore[2]，Total Recall[3]，DHash++[4]等)利用多个数据节点进行存储的，其目标是要保持数据的长期可靠存储.然而数据规模发展到今天，存储节点的损坏已经是一种常态，而不是偶然事件.例如Facebook部署的Hadoop[5]集群中共有3 000多个节点，涉及45 PB数据，日平均失效节点数为22个，最高日失效节点数达到100个.因此如何保障数据存储的可靠性就成为分布式存储系统研究的首要问题.

保证数据存储可靠性的方法主要是引入冗余信息来提高系统的容错能力，从而在发生节点失效时能够进行修复.通常有两种策略：一种是数据复制策略[6-8]，一种是纠删编码策略.数据复制策略的好处是简单易实现，但是数据量太大.如HDFS[9]和GFS[10]就是采用3副本复制的策略，其数据存储量相当于膨胀了3倍.利用纠删编码策略数据量膨胀较小，但要求节点有一定的计算能力.目前关于纠删码的研究是分布式存储方案中的热点.

纠删码本来起源于通信领域的信道编码，现已广泛应用于存储系统中.研究人员已提出了许多可行的纠删码方案用于分布式存储系统.Wu[11]利用网络编码理论设计了一种部分精确修复纠删码，能够精确修复系统部分的单节点故障.Papailiopou-los等[12]利用异或运算设计了一种简单再生码，先进行纠删编码，再进行某种方式的异或编码，它能够对单节点损坏进行精确修复.Salim等[13]利用重复编码设计了能修复部分节点故障的MDS编码[14].Changho等[15]利用网络编码理论以及矩阵特征向量设计了一种MDS纠删码，可以精确修复单节点故障.蔡鸾佳[16]考虑到安全问题，将同态指纹检验码技术应用到纠删编码方案中去，设计了具有拜占庭容错性能的存储协议.李谢华等[17]考虑到云存储中的访问控制安全问题，设计了基于属性加密的访问控制方案.然而这些方案都没有考虑编码解码时的效率问题.由于纠删码在编码解码过程中都要用到大量的有限域上的矩阵运算，运算代价是比较高的，所以编解码效率是个不能忽视的问题.

本文利用一种特殊的纠删码——再生码来实现分布式存储方案，它除了具有纠删码的容错性能之外，还能使修复损坏节点时从各个帮助节点下载的数据量——修复带宽达到最小，并且由于采用柯西型矩阵作为编码矩阵，使得修复效率和数据重建效率都有较大提高.

1 相关知识

纠删编码是一种重要的数据容错策略，常用于构建高可靠性分布式存储系统.再生码是在其基础上发展起来的一种特殊的纠删码，它继承了纠删码的性质，同时在修复损坏的节点时无需下载源数据大小的数据量，从而可以节省网络带宽.下面介绍纠删码和再生码的相关知识.

1.1 MDS纠删码

定义1 (n,k)纠删码.所谓(n,k)纠删码[14]是指这样一种编解码方法：发送方将k个长度均为α的源数据包编码为n个长度为α的数据包，其中要求n>k.接收方收到了这n个编码数据包中的m个后(这里m≥k)，通过解码算法就能够重构出原来的k个源数据，而收到的数据包少于k个时则不能重构出源数据.其原理如图1所示.

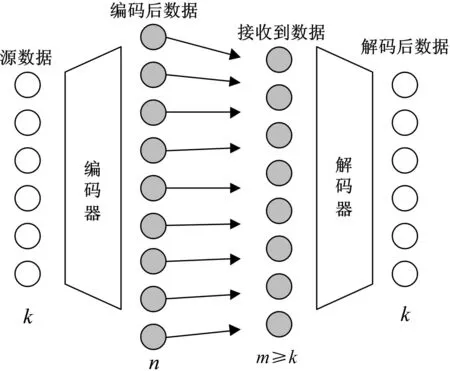
图1 (n,k)纠删码原理图Fig.1 Principle of (n,k) erasure coding

如果接收方能够从收到的m个数据包中只要任意选k个都能重构出原来的k个源数据包的话，那么就称这种编码为极大距离可分码(Maximum Distance Separable,MDS).通常也称这种编码满足MDS性.从冗余折中角度来讲，MDS码是一种最优纠删码，因为k个数据包是能够包含所有源数据信息的最小值.

根据纠删码的性质，可以将其运用到分布式存储系统的冗余容错中.当某一个节点损坏的时候，只需要从剩余的节点中选取k个或者k个以上节点下载数据，并利用解码算法恢复出源数据，再对源数据进行编码生成损坏节点的数据包，这就完成了节点的修复.然而在这一过程中，整个的网络通信量是kα，通常也称之为修复带宽.可见对于一般的MDS码来说，修复一个损坏节点需要下载整个源数据文件大小的数据量，带宽消耗是相当高的.事实上，如果只是修复一个损坏节点，修复带宽是可以小于kα的，这就要用到再生码.

1.2 再生码

Dimakis等[18]于2007年首先提出了利用网络编码的方法来优化和设计纠删码，并将其应用于分布式存储系统中，有效降低了数据修复过程中的通信开销，并首次把这种基于网络编码的纠删码命名为再生码.

定义2 再生码.假设源数据文件中单个符号是有限域GF(q)中的元素，文件长度为B，将其编码存储到n个节点，每个节点存储大小为α的编码数据.如果某个节点损坏，替代节点就从剩余的n-1个节点中连接任意d(其中k≤d≤n-1)个并下载相关数据进行修复，从每个节点下载的数据量为β≤α.这d个参与帮助修复的节点就称为帮助节点(Helping Node)，用于修复而下载的总数据量dβ就称为修复带宽(Repair Bandwidth)，它小于原始文件总大小B.这样就可以用{n,k,d,α,β,B}这6个参数来表示一个再生码.

再生码的所谓“再生性”主要体现在对损坏节点数据的再生上，如果要恢复源数据，则只要按其纠删码的解码过程操作即可.文献[19]指出，根据修复出来的数据包与损坏节点的数据包是否完全一致，再生码又可以分为3类修复模式：精确修复、部分精确修复和功能性修复.在精确修复再生码中，损坏节点的数据包能被完全精确的再生出来；而在功能性修复再生码中，修复出来的数据包可能与损坏节点的数据包并不完全一致，但是仍然满足MDS性；而部分精确修复再生码则介于两者之间，其对损坏节点的系统部分数据是精确修复的，而对冗余部分则可能是功能性修复的.

再生码的概念提出以后，Wu等[20]根据网络流理论中的最大流最小割原理给出了再生码参数必须满足的一个条件：

(1)

在d固定的情况下，最小化α可以使得总冗余存储量最小；最小化β可以使得总修复带宽最小.以上这两种情况也就分别称为最小存储再生码(Minimum Storage Regeneration，简记为MSR)和最小带宽再生码(Minimum Bandwidth Regeneration，简记为MBR).然而根据式(1)可以推知，不可能同时最小化α和β.文献[17]给出了实现MSR和MBR需满足的条件：

(2)

(3)

αMBR=d

(4)

也就是说，在构造的再生码方案中，其参数只要满足以上条件，就可以使修复带宽达到最小.本文主要研究精确修复模式的最小带宽再生码(Exact-Repair MBR，简记为ER-MBR).此时，由于βMBR=1，αMBR=d，因而参数集{n,k,d,α,β,B}就可以简化为{n,k,d,B}.下面详细介绍ER-MBR的实现原理.

2 实现原理

将源数据中的单个符号看作是有限域GF(q)中的元素，则ER-MBR的构造过程可采用有限域上的矩阵运算来表示.将源数据向量[b1,b2,…,bB](其中bi∈GF(q)；i=1,…,B)按一定规则存放在阶为d×d的数据矩阵M中，再选择一个阶为n×d的矩阵R作为编码矩阵，它是预先定义并独立于数据矩阵的，并且在选取时要求它的每个行数为d的子方阵都是可逆的.编码后的数据用再生码矩阵C来表示，它是一个阶为n×d的矩阵，则再生码可以用以下矩阵乘法公式表示：

Cn×d=Rn×d×Md×d

(5)

下面从数据的编码分发、源数据的重构和损坏节点的修复3个方面讲解ER-MBR的实现原理.

2.1 数据的编码分发

再选择一个n×d阶的矩阵R作为编码矩阵，按照式(5)进行运算，得到再生码矩阵C，C的第i行(i=1,…,n)包含的d=αMBR个元素构成的向量ci就由第i个节点存储.这样就把原始数据编码分布到了n个存储节点上.记编码矩阵R的第i行的向量为ri，则第i个存储节点的数据向量就可表示为：ci=riM.其实现过程如图2所示.

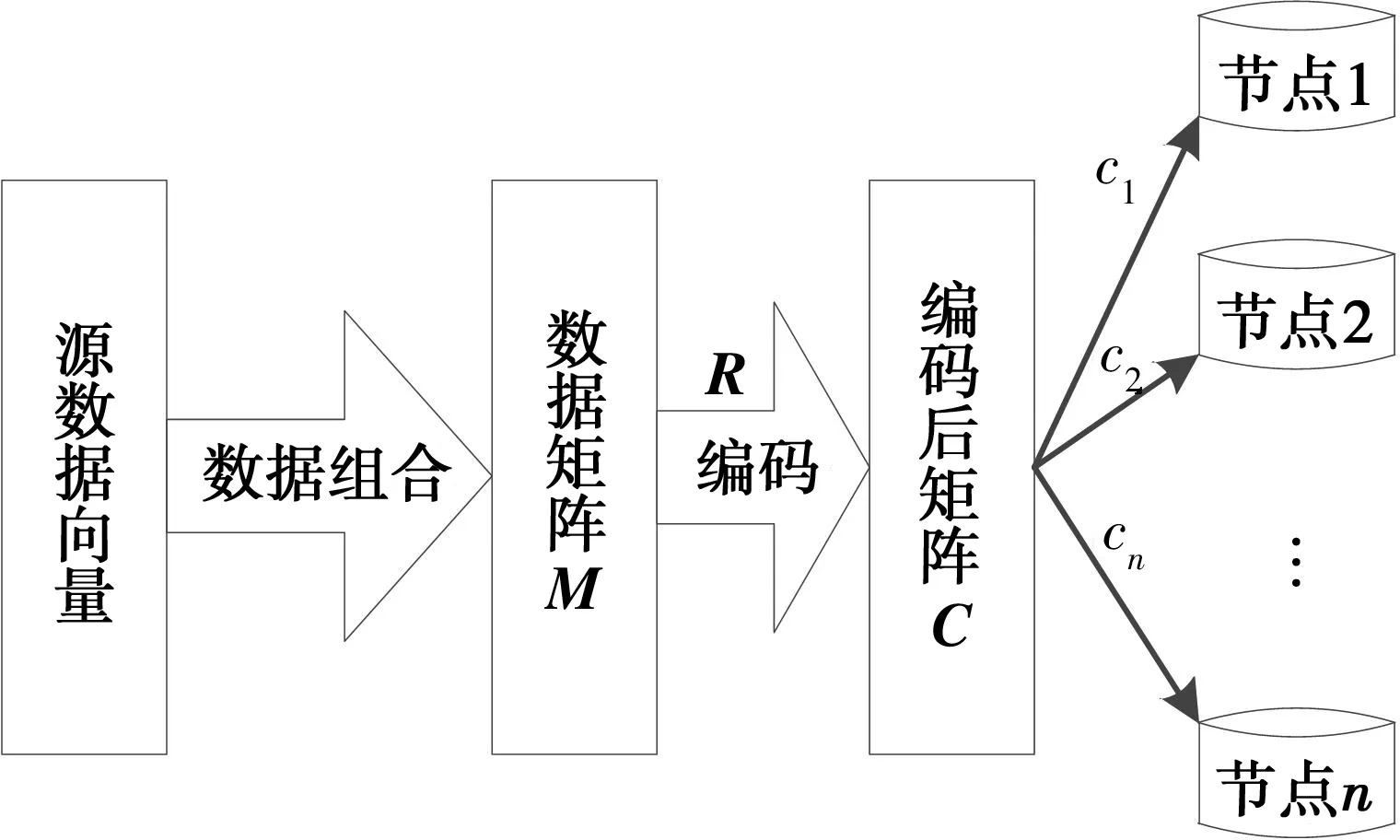
图2 源数据的编码分发Fig.2 Distribution of coded source data

2.2源数据的重构

要重构源数据，数据汇聚点DC需要从n个存储节点中的任意k个节点{i1,i2,…,ik}中下载编码数据向量，组成再生码数据矩阵CDC，再从编码矩阵R中选取相对应的行向量{ri1,ri2,…,rik}组成解码矩阵RDC，根据解码算法即可重构出源数据文件，其实现过程如图3所示.以下定理1说明了数据重构的充分性.

图3 源数据的重构Fig.3 Reconstruction of source data

定理1 在当前的ER-MBR编码方式下，所有的B个源数据符号都可以通过连接n个存储节点中的任意k个节点并下载相应数据进行线性变换而予以重构.

证 记RDC=[WDCZDC]表示编码矩阵R中与k个汇聚节点相关的行组成的k×d阶子矩阵，WDC是k×k阶方阵，由编码矩阵的性质可知它是可逆的.

由于，

[WDCS+ZDCTtWDCT]

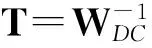
(6)

从而可以重构整个M.

证毕.

2.3 失效数据节点的修复

在式(5)所定义的ER-MBR分布式存储系统中，如果某一个节点损坏，则替换节点可以从剩下的n-1个节点中任意连接d个并下载编码数据，再根据这d个帮助节点所对应的行数从编码矩阵R中选取相应的行向量组成修复矩阵Rrepair，显然RrepairM就是替换节点从帮助节点处下载的再生码数据矩阵，然后根据ER-MBR的解码算法即可计算出损坏节点的数据.在这一过程中无需重建源数据就可以直接生成损坏节点的数据，这就比普通的纠删码简化了运算.其实现过程如图4所示.以下定理2说明了失效节点数据修复的充分性.

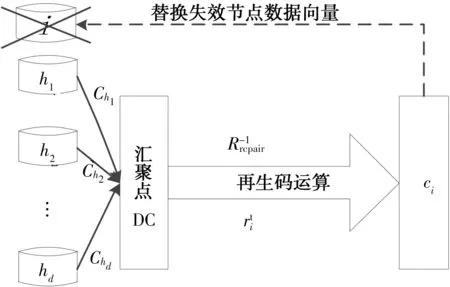
图4 失效节点数据的再生Fig.4 Data regenerating of failed node

定理2 在当前的ER-MBR编码方式下，如果第i个节点损坏，则替换节点通过从剩下的n-1个节点中任意连接d个并下载相应数据即可再生出该损坏节点存储的数据向量ci.

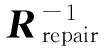
(7)

3 基于柯西矩阵的ER-MBR的实现

从上述实现原理可以看出，再生码的运算主要是有限域上的矩阵运算.由于目前计算机是以8比特的一个字节为信息存储的最小单位，所以可将源数据的最小符号看作是有限域GF(28)中的元素.有限域中元素的加法和减法等价，都是异或运算.乘法运算则需要用到本原多项式，具体方法是将有限域中元素的二进制表示式看作是降幂多项式的系数，两个元素相乘就相当于多项式相乘，再对本原多项式求模，所得结果多项式再转化为向量.本实现中取本原多项式m(x)=x8+x4+x3+x2+1作为模多项式.从式(5)可以看出，再生码的构造主要取决于编码矩阵R的选取.原则上只要该矩阵的任何一个子方阵都是可逆的就可以作为编码矩阵，在此我们采用柯西型矩阵来作为编码矩阵，下面先给出柯西矩阵的定义.

定义3 柯西矩阵(Cauchy Matrix)[21].

如果{xi|i=1,…,m}和{yj|j=1,…,n}都是域GF(q)中的元素，且满足：1){xi|i=1,…,m}两两不同；2) {yj|j=1,…,n}两两不同；3)xi+yj≠0；则形式为

对于一个n阶的柯西方阵，其行列式为：

(8)

由柯西矩阵的定义易知，以上行列式(8)永不等于零.同时易知柯西矩阵的任何子方阵也是柯西型的，这也就意味着柯西矩阵的任何子方阵都是可逆的.另外柯西矩阵的乘法运算及求逆运算效率都比较高，这些良好的性质，使我们考虑以其作为编码矩阵.

下面以一个GF(28)上的参数为 (n,k,d,B)=(6,3,4,9)的ER-MBR为实例来说明实现过程.

3.1 数据矩阵的组装

引理 1 若系统(1)的全局领导者1匀速运动,则对任意的t>0,有E‖vi(t)‖≤D(1≤i≤N),其中D是一个大于0的常数。

由参数为(n,k,d,B)=(6,3,4,9)可知源文件长度为9个字节，不妨记为[u1,u2,…,u9]，其中ui都是有限域GF(28)中的元素.则组装后的数据矩阵为：

3.2 编码矩阵的选取

按柯西矩阵的定义，从GF(28)中选取合适的元素即可构成编码矩阵R，比如取xi=0,1,2,3,4,5； yj=6,7,8,9则有：

3.3 数据的编码分发

根据式(5)易知，编码后的再生码矩阵为：

再生码矩阵C的每一行向量就相应分发给每一节点，即第i行向量ci就分发给第i个节点(i=1,…，6).如分发给节点1的向量就为：

3.4 源数据的重构

由于ER-MBR是基于纠删码的，所以通过连接k个节点就可以重构出源数据，本例中只要连接3个节点即可.假设从节点1，2，3下载相应数据来重建源数据.从这3个节点可接收到的数据为：

而编码矩阵R的子方阵

3.5 失效节点的数据修复

因为修复带宽为d=4，所以若某一节点失效，只要连接4个帮助节点就可以进行修复替换.假设节点5失效，我们选取节点2，3，4，6作为帮助节点来进行修复，首先易知修复矩阵为：

从而它的逆矩阵为：

从节点2，3，4，6收到的数据组成的再生码矩阵为：

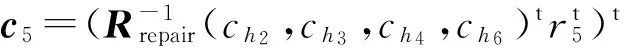
图5 失效节点5的修复Fig.5 Repairing of failed node five

4 理论分析

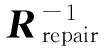
对于一般的矩阵R，如果其元素是在有限域GF(28)中随机选取，Chou等[22]指出，这种矩阵可逆的概率可以达到99.6%，所以理论上也是可以用来作为再生码的编码矩阵的.然而对于一般的矩阵，其逆矩阵的计算复杂度是相当高的.Copersmith等[23]已经将其复杂度上界降为O(n2.496)，是目前已知最好的结果.

再来看范德蒙矩阵求逆的情况.若xi∈GF(28)，i=1,…,n，且xi两两不同，则形如

的矩阵就称为范德蒙矩阵，易知其行列式为：

最后来看柯西矩阵的求逆.文献[25]指出，记一个n阶的柯西型矩阵C的逆矩阵为C-1=(dij)n×n，i,j=1,2,…,n其元素dij可由下式给出：

利用该算法，可以将柯西矩阵求逆的复杂度降低到O(nlg2n).

比较以上3种复杂度O(n2.496)，O(n2)和O(nlg2n)，易知柯西矩阵求逆的复杂度是最低的.另外还要指出的是，如果采用范德蒙型矩阵作为再生码的编码矩阵，则在节点修复过程中，其修复矩阵未必还是范德蒙型的，只能按一般的矩阵来处理，这样其求逆的运算量将会更大.而采用柯西矩阵的再生码，其修复矩阵仍然是柯西型矩阵，存在如文献[25]所指出的快速求逆算法，因此修复效率更高.

5 实验分析

为了验证本文构造方法的可行性，我们选取随机生成的文件，通过ER-MBR码编码算法生成分布到各节点的数据，再模拟当某一节点失效时，采用不同的编码矩阵时的节点修复效率.硬件环境是联想Y700电脑，英特尔酷睿i7-6700 CPU(2.6 GHz主频)，16 G内存.软件环境是在windows 10操作系统下采用MatlabR2014a编程语言进行编程实现.实验分为两种，一是在测试文件大小为10 kB的固定值情况下，采用参数为(16,3,d,B)的ER-MBR码，其中修复带宽d进行变化，相应地参数B随d值而变化；一种是采用固定参数为(16,3,10,52) 的ER-MBR码情况下，测试文件大小进行变化.所有运算都是在有限域GF( 28)上进行.实验结果如图6和图7所示.

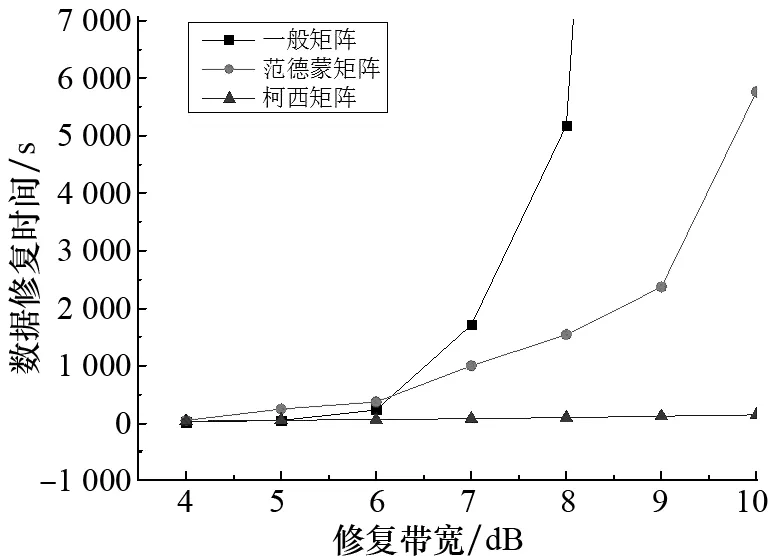
图6 文件大小固定时修复效率对比Fig.6 Comparison of repairing efficiency while file length unchanging

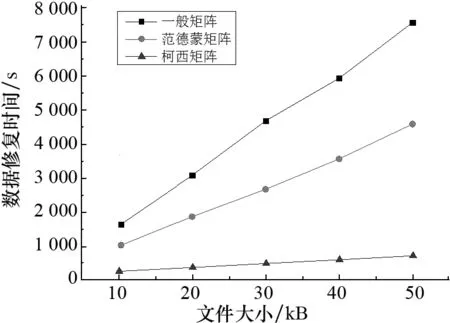
图7 文件大小变化时修复效率对比Fig.7 Comparison of repairing efficiency while file length changing

从图6可以看出，随着修复带宽d的增大，采用一般矩阵或范德蒙矩阵作为编码矩阵的ER-MBR码，数据修复时间变化较快，而采用柯西矩阵则变化不明显，说明采用柯西矩阵作为编码矩阵的ER-MBR码其节点修复效率受d的影响不大，在采用多节点修复策略的时候优势非常明显.

从图7可以看出，参数固定时，采用各种编码矩阵的ER-MBR码其修复时间都与文件大小成正比关系，但是采用柯西矩阵作为编码矩阵的ER-MBR码其节点修复效率明显更高.

6 结 论

再生码是一种特殊的纠删码，不但能重建源数据，还能在不需要恢复源数据的前提下恢复失效节点的数据，从而节省修复带宽.我们描述了精确修复最小带宽再生码的概念并给出其实现条件，并利用柯西矩阵作为编码矩阵对其进行了优化.理论分析和实验结果表明，在分布式存储系统中，以柯西矩阵作为ER-MBR码的编码矩阵，能有效提高修复效率和重建效率，但是否还存在更好的编码矩阵呢？这是个开放问题，有待进一步研究.另外，柯西矩阵本身可能还可以进一步优化，以构造更容易实现解码效率的柯西矩阵出来，这也是个值得研究的方向.

[1] ELERATH J G. RAID-6 system reliability dependence on recovery,disk scrubbing,and group size[C]//Proceedings of 2016 Annual Reliability and Maintainability Symposium. Tucson,Arizona,USA: IEEE Computer Society,2016:25-28.

[2] RHEA S,WELLS C,EATON P,etal. Maintenance-free global data storage[J]. IEEE Internet Computing,2001,10(9):40-49.

[3] BHAGWAN R,TATI K,CHENG Y C,etal.Total recall: system support for automated availability management[C]//Proceedings of USENIX the First Symposium on Networked Systems Design and Implementation. San Francisco,California,USA,2004:337-350.

[4] DABEK F,LI J,SIT E,etal. Designing a DHT for low latency and high throughput[C]//Proceedings of USENIX the First Symposium on Networked Systems Design and Implementation.San Francisco,California,USA,2004:85-89.

[5] SATHIAMOORTHY M,ASTERIS M,PAPAILIOPOULOS D,etal. Xoring elephants: novel erasure codes for big data[C]//Proceedings of the 39th International Conference on Very Large Data Bases. Riva del Garda,Trento,Italy,2013:325-336.

[6] 王意洁,孙伟东,周松,等.云计算环境下的分布存储关键技术[J].软件学报,2012,23(4):962-986.

WANG Yijie,SUN Weidong，ZHOU Song,etal. Key technologies of distributed storage for cloud computing[J].Journal of Software,2012,23(4):962-986.(In Chinese)

[7] 罗象宏,舒继武.存储系统中的纠删码研究综述[J].计算机研究与发展,2012,49(1):1-11.

LUO Xianghong,SHU Jiwu. Summary of research for erasure code in storage system[J].Journal of Computer Research and Development,2012,49(1):1-11.(In Chinese)

[8] 李挥,张宇蒙,陈俊.大数据环境下的可靠存储技术思考[J].中兴通讯技术,2015,21(5):27-31.

LI Hui,ZHANG Yumeng，CHEN Jun. Reliable storage technologies for big data[J].ZTE Technology Journal,2015,21(5):27-31.(In Chinese)

[9] SHVACHKO K,KUANG H,RADIA S,etal. The hadoop distributed file system[C]//Proceedings of the 26th IEEE Symposium on Mass Storage Systems and Technologies. Lake Tahoe,Nevada,USA: IEEE Computer Society,2010:1-10.

[10]WANGMengdi,LI Bo,ZHAO Yongxin,etal. Formalizing google file system[C]//Proceedings of the 20th IEEE Pacific Rim International Symposium on Dependable Computing. Singapore,2014:190-191.

[11]WU Yunnan. A construction of systematic MDS codes with minimum repair bandwidth[J].Information Theory,2011,57(6):3738-3741.

[12]PAPAILIOPOULOS D S,LUO Jianqiang,DIMAKIS A G,etal.Simple regenerating codes: network coding for cloud storage[C]//Proceedings of the 31st Annual IEEE International Conference on Computer Communications.Orlando,Florida,USA,2012:2801-2805.

[13]SALIM E R,RAMCHANDRAN K. Fractional repetition codes for repair in distributed storage systems[C]//Proceedings of the 51st Annual Allerton Conference on Communication.Control,and Computing.Monticello,Illinois,USA,2010:1510-1517.

[14]RIZZO L.Effective erasure codes for reliable computer communication protocols[J].ACM Computer Communication,1997,27(2):24-36.

[15]CHANGHO S,RAMCHANDRAN K.Exact-repair MDS code construction using interference alignment[J].Information Theory,2011,57(3):1425-1442.

[16]蔡鸾佳.拜占庭容错纠删码分布式存储协议[J].计算机系统应用,2012,21(2):98-103.

CAI Luanjia. Byzantine fault-tolerant erasure coded distributed storage protocol[J].Computer Systems & Applications,2012,21(2):98-103.(In Chinese)

[17]李谢华,张蒙蒙,刘鸿,等. 基于MA-ABE的云存储访问控制方法[J].湖南大学学报：自然科学版,2015,42(10):133-140.

LI Xiehua,ZHANG Mengmeng,LIU Hong,etal.Multi-authority ABE for access control in cloud storage[J].Journal of Hunan University:Natural Sciences,2015,42(10):133-140.(In Chinese)

[18]DIMAKIS A G,GODFREY P B,WU Y,etal.Network coding for distributed storage systems[J].IEEE Transactions on Information Theory,2010:4539-4551.

[19]DIMAKISA G,RAMCHANDRAN K,WU Y,etal.A survey on network codes for distributed storage[J].Proceedings of the IEEE,2011,99(3):476-489.

[20]WU Y,DIMAKIS A G,RAMCHANDRAN K.Deterministic regenerating codes for distributed storage[C]//Proceedings of the 45th Annual Allerton Conference on Control,Computing and Communication.Urbana-Champaign,Illinois,USA,2007:1354-1362.

[21]慕建君,路成业,王新梅.关于纠删码的研究与进展[J].电子与信息学报,2002,24(9):1276-1281.

MU Jianjun,LU Chengye,WANG Xinmei.Research and development about erasure code[J].Journal of Electronics and Information Technology,2002,24(9):1276-1281.(In Chinese)

[22]CHOU P A,WU Y,JAIN K.Practical network coding [C]//Proceedings of the 51st Annual Allerton Conference on Communication,Control,and Computing.Monticello,Illinois,USA,2003:114-120.

[23]COPERSMITH D,WINOGRAD S.On the asymptotic complexity of matrix multiplication[C]//Proceedings of the 22nd Annual Symposium on Foundations of Computer Science. Nashville,Tennessee,USA,1981:82-90.

[24]FINCKT,HEINIG G,ROST K.An inversion formula and fast algorithm for Cauchy-Vandermonde matrices[J].Linear Algebra and Its Applications,1993,183(1):179-191.

[25]WUX,WANG H,YAN Z. Erasure codes for broadcasting small files over erasure channels with low bandwidth[C]//Proceedings of the 42nd Annual Conference on Information Sciences and Systems.Princeton,New Jersey,USA,2008:556-561.

Study of Minimum Bandwidth Regeneration Codes Based on Cauchy Matrix

SONG Hailong1，2†，WANG Weiping2，XIAO Yalong1

(1.School of Information Science and Engineering，Central South University，Changsha 410083，China；2.School of Information Science and Engineering，Jishou University，Jishou 416000，China)

The failures of node are the common phenomena in the massive distributed storage system.To prevent the data loss,the system must solve the problem of self-repairing for failed nodes.Using regenerating codes,the data of failed nodes can be recovered without downloading the whole source file,so repairing bandwidth can be effectively saved.This paper presents an exact-repair minimum bandwidth regeneration code (ER-MBR) by using Cauchy matrix as coding matrix.ER-MBR can exactly repair the failed nodes.The whole process of coding,decoding and node repairing is demonstrated in the finite fields by an instance.Theoretical analysis and simulation experiments prove that by using Cauchy matrix as coding matrix,the operation efficiency of this algorithm is better than that of using Vandermonde matrix or random matrix.

erasure codes；egenerat codes；network coding；Cauchy matrix；Vandermonde matrix；distributed storage

1674-2474(2017)08-0152-09

10.16339/j.cnki.hdxbzkb.2017.08.023

2016-12-11

国家自然科学基金资助项目(61173169,61363073),National Natural Science Foundation of China(61173169,61363073)

宋海龙(1977—)，男，山东平度人，中南大学博士生，吉首大学讲师

†通讯联系人，E-mail:highsong@126.com

TP393

A