传统木结构单向直榫节点转动弯矩-转角关系理论分析*

谢启芳,王龙,郑培君,张利朋,钱春宇

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055;2.中国建筑第七工程局有限公司,河南 郑州 450004;3.机械工业勘察设计研究院有限公司，陕西 西安 710043)

传统木结构单向直榫节点转动弯矩-转角关系理论分析*

谢启芳1†,王龙1,郑培君2,张利朋1,钱春宇3

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055;2.中国建筑第七工程局有限公司,河南 郑州 450004;3.机械工业勘察设计研究院有限公司，陕西 西安 710043)

以传统木结构中最简单的单向直榫节点为研究对象，分析其受力机理，推导了单向直榫节点转动弯矩-转角理论计算公式，并借助试验数据对该公式进行了验证，理论计算结果与试验结果吻合较好.以理论公式为基础，对影响单向直榫节点转动弯矩的参数进行了分析，结果表明：当榫头长度与柱径之比小于1时，榫头长度的增加能显著提高单向直榫节点的转动弯矩和初始转动刚度；榫头宽度的增加同样能够提高单向直榫节点的转动弯矩以及初始转动刚度；摩擦系数的增大能够在一定程度上提高节点的转动弯矩，但对节点的初始转动刚度影响不大.研究结果可为传统木结构的抗震性能评估和修缮加固提供一定的参考.

传统木结构；单向直榫节点；受力机理；弯矩-转角关系；理论分析

榫卯连接是我国传统木结构的主要特点之一[1]，由榫头和卯口组成.榫卯节点具有较强的半刚性连接特性[2]，是木结构中的关键部位.历次震害表明，地震会对传统木结构的节点造成不同程度的破坏[3]，因此研究榫卯节点的受力性能至关重要.

近几十年来国内外学者对传统木结构榫卯节点进行了大量的研究，也提出了相关的弯矩-转角模型.如Kishi和Chen[4]以钢结构的节点为研究对象，提出了三参数幂函数模型，虽然在木结构中得到广泛应用,但其只能笼统地描述传统木结构榫卯半刚性连接特性，不能描述榫卯尺寸等因素的影响，具有一定的局限性.赵鸿铁等[5]和杨艳华等[6]利用试验数据,拟合出了不同的弯矩-转角关系方程.谢启芳等[7]基于燕尾榫节点受力机理的分析,推导了燕尾榫节点弯矩-转角理论计算公式.潘毅等[8]以透榫节点为研究对象，建立了考虑节点拔榫量影响的弯矩-转角力学模型.

可以看出，已有的研究主要以燕尾榫和透榫为主，少有涉及单向直榫等其他类型的榫卯节点.基于此，本文以传统木结构单向直榫节点为研究对象，分析了其受力机理，推导了转动弯矩-转角理论计算公式，并与试验结果进行了对比，结果吻合良好.

1 单向直榫节点受力机理

1.1 单向直榫节点营造形式

单向直榫节点是直榫节点中最简单的一种形式，榫头为矩形，直接穿插到柱子的卯口内，如图1所示.

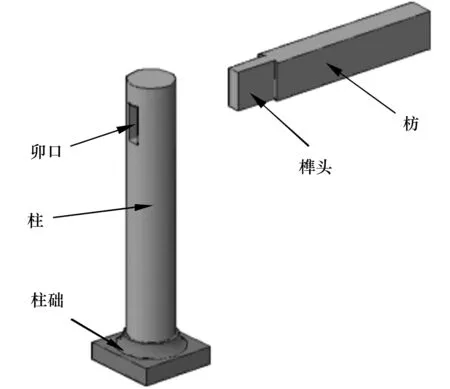
图1 单向直榫节点示意图Fig.1 Diagram of the straight mortise-tenon joint

虽然榫卯连接削弱了木构件的截面，一定程度上降低了节点的抗转动能力，但却具有“大变形，小刚度”的柔性特点.在地震作用中，榫卯节点变形较大，可吸收部分能量，减小结构的地震响应，构件间的摩擦滑移又能起到耗能减震的作用，从而使木构架具有较好的抗震性能，是一种介于刚性节点和铰节点之间的半刚性节点.在中国传统木结构承重构架的节点中，直榫使用最广泛,单向直榫节点又是最基本最简单的.因此本文以单向直榫节点为基础，分析其受力机理.

1.2 单向直榫节点抗弯受力机理分析

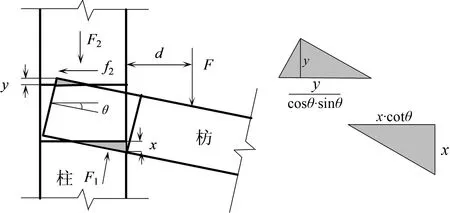
图2 单向直榫节点受力分析Fig.2 Force analysis for the straight mortise-tenon joint

图2为单向直榫节点受力分析示意图.当转动弯矩较小时，节点依靠榫卯间的静摩擦力来抵抗外力；随着转角的增大，当水平外力超过最大静摩擦力时，榫头和卯口就会出现相对滑移.榫头将会以卯口下表面边缘为轴发生转动，榫头下表面出现受压区域(图2中下三角形阴影部分)，但因为只发生转动，因此该区域只产生压力F1，而没有摩擦力，F1的方向始终垂直于额枋，同时榫头上表面也会出现受压区域(图2上三角形阴影部分)并有滑动趋势，从而产生压力F2和摩擦力f2，F2平行于柱子顺纹方向，f2垂直于柱子顺纹方向，如图2所示.因为单向直榫节点上下是对称的，所以其正向与反向转动的变形形态和受力状态相同.由此可见，单向直榫的转动弯矩主要由榫头上下表面的挤压力和上表面挤压面的摩擦力提供.由此推断，单向直榫在承受弯矩作用时，榫颈处产生一定的顺纹拉应力、横纹压应力和剪应力，当达到极限弯矩时，将发生纤维拉断的弯曲破坏.

2 单向直榫节点转动弯矩-转角关系

2.1 基本假定

由受理机理分析可知，节点的受力范围主要发生在榫卯接触区，通过榫卯挤压变形和摩擦滑移来抵抗外力，且节点在正反2个方向的受力相同.为了简化计算，采取以下假定：

1)试件破坏仅发生在节点区域，枋和柱仅起传力作用，不考虑枋和柱的弯曲效应.

2)节点转动时，榫头颈部仅绕着卯口边缘转动，没有相对位移，而榫头端部则产生相对卯口的位移[9].

3)在受压荷载作用下榫头实际上处于多点不均匀的受力状态，自身变形相对较小，根据小变形假定，忽略其弯曲变形.

4)节点受弯矩作用时，卯口为顺纹受压，榫头为横纹受压，由于木材顺纹受压弹性模量一般为横纹受压弹性模量的10倍以上，因此忽略卯口的挤压变形，仅考虑榫头受压变形.

5)木材沿额枋、柱纵向为顺纹方向，其横纹受压本构关系采用双线性强化模型，如图3所示，且应力应变关系仍符合胡克定律[10].

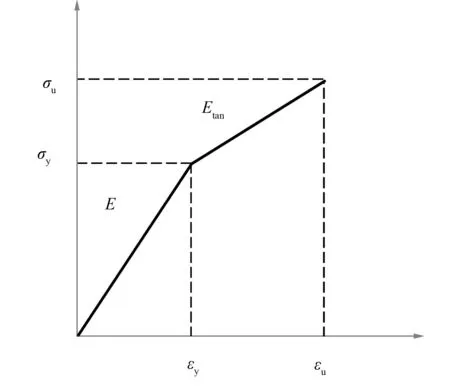
图3 木材横纹受压应力-应变关系Fig.3 Stress-strain relationship of wood perpendicular to the grain under compression

2.2 单向直榫节点弯矩-转角理论公式推导

单向直榫节点尺寸示意图如图4所示.

单向直榫节点的理论分析过程分为3个阶段：1)F1受力区域和F2受力区域均未出现塑性变形；2)F1受力区域出现塑性变形，F2受力区域未出现塑性变形；3)F1受力区域和F2受力区域均出现塑性变形.

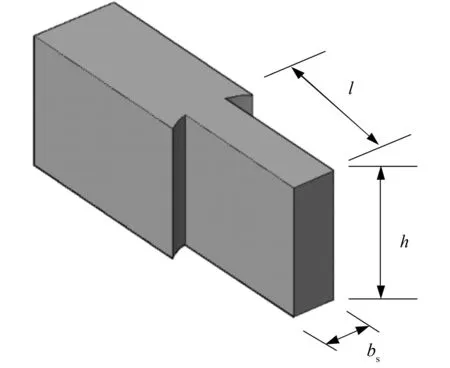
图4 单向直榫榫头尺寸示意图Fig.4 Size schematic diagram of the straight tenon

榫头上下表面受压区产生的最大应变分别为:

(1)

式中：x为榫头下表面最大受压高度；y为榫头上表面最大受压高度；he为榫头有效受压高度.文献[11]试验中的应变测试数据表明，在榫头高1/2处的应变接近于0，故取he=h/2.

(2)

弹性模量在不同转角θ下的变化规律：

(3)

式中：E⊥为木材径向横纹受压的弹性模量；E⊥tan为木材径向横纹受压进入塑性阶段后的切线模量.

χ(θ)是考虑木材弹性模量在不同角度作用时的增大系数，可以按照Hankinson公式计算：

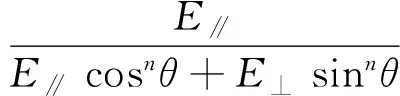
(4)

式中：E∥为木材顺纹受压弹性模量，n=3.1.

由图2可以得到几何关系：

h+x+y=Lsin(θ+φ).

(5)

由图2的平衡关系可以得到水平和竖直方向的平衡方程：

F1sinθ-μF2=0,

(6)

F1cosθ-F2=F.

(7)

式中：μ为木材摩擦系数.

2.2.1 第一阶段

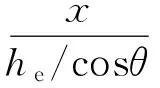
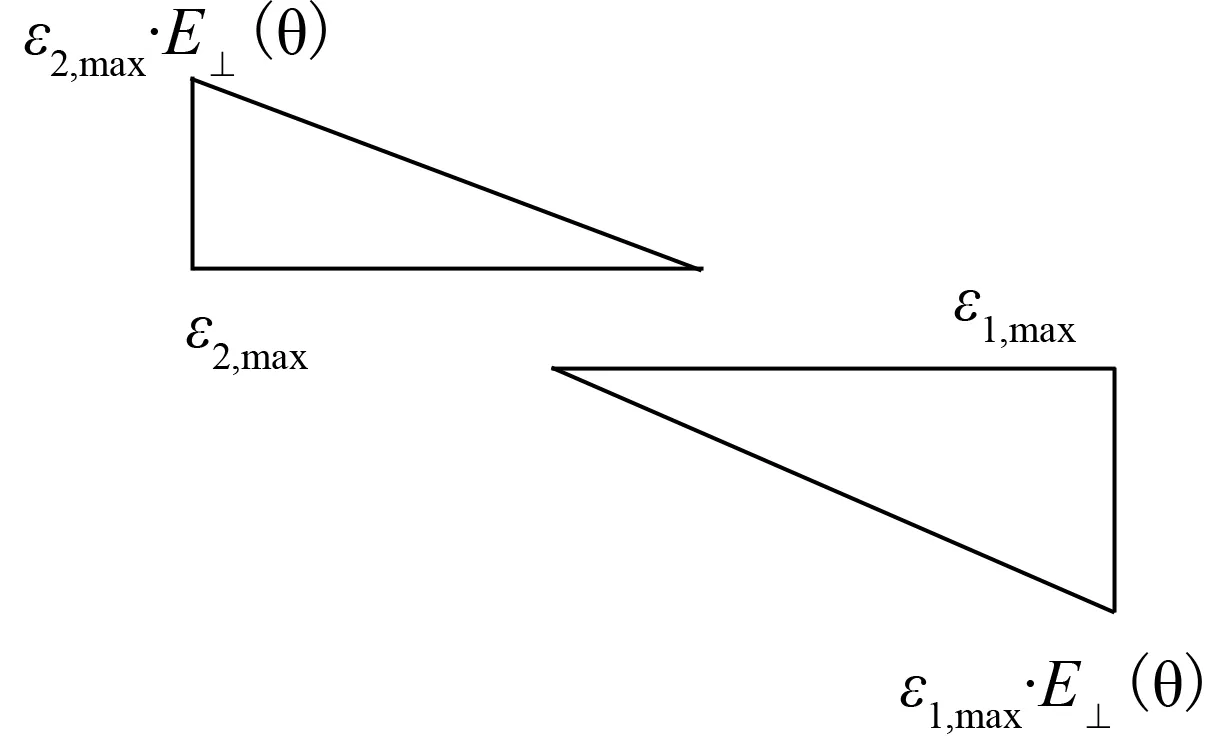
图5 单向直榫节点转动第一阶段的应力-应变关系图Fig.5 Stress-strain relationship during the firststage of the straight tenon

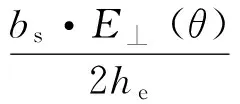
(8)

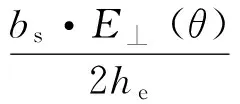
(9)

根据式(5)(6)(8)(9)可得x和y关于θ的方程，进而解得x与y的具体数值.

代入式(7)(8)(9)可得：

(10)

2.2.2 第二阶段

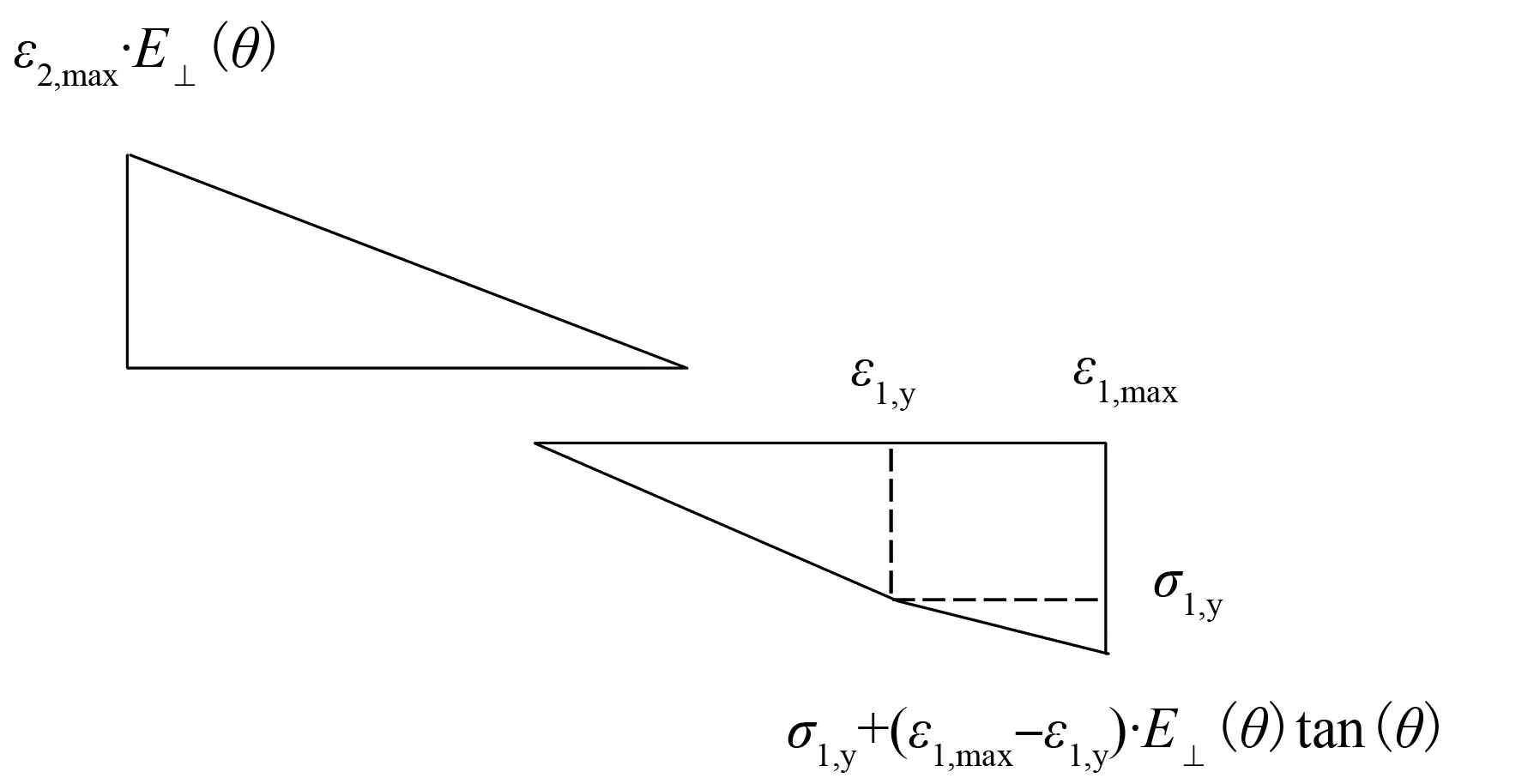
图6 单向直榫节点转动第二阶段的应力-应变关系图Fig.6 Stress-strain relationship during the second stage of the straight tenon

(11)

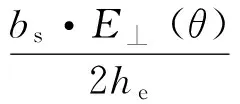
(12)

根据式(5)(6)(11)(12)可得x和y关于θ的方程，进而解得x与y的具体数值.

代入式(7)(11)(12)得：

(13)

2.2.3 第三阶段

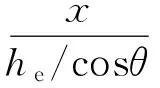
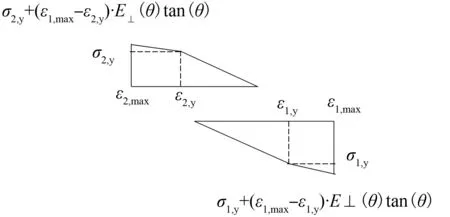
图7 单向直榫节点转动第三阶段的应力-应变关系图Fig.7 Stress-strain relationship during the third stage of the straight tenon

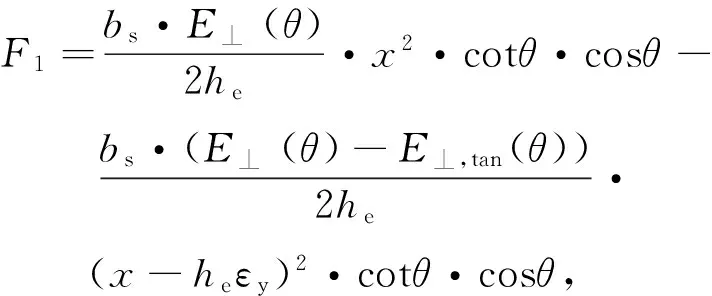
(14)

(15)

根据式(5)(6)(13)(14)可得x和y关于θ的方程，进而解得x与y的具体数值.

代入式(7)(14)(15)得：

(16)

临界转角θ1，θ2和θu可利用式(1)以及x和y关于θ的方程，并借助计算分析软件MATLAB反解求得.

3 单向直榫节点转动弯矩-转角理论结果验证

文献[11]对单向直榫节点进行了拟静力试验，将试验中试件的参数代入本文推导的公式进行计算，并与试验结果进行对比.

文献[11]对缩尺比例为1∶4.8的2个完全相同的单向直榫节点进行了试验，模型详细尺寸如图8和表1所示，各项力学性能参数如表2所示.加载方式分别为单向加载(试件1)和低周反复加载(试件2).

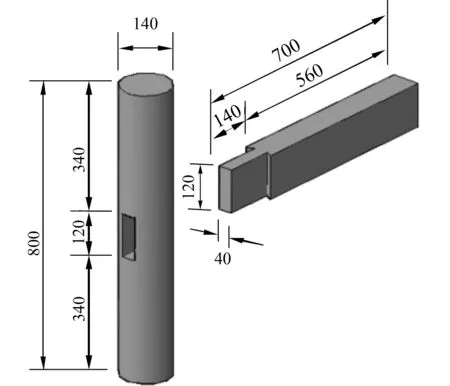
图8 试验模型尺寸(单位：mm)Fig.8 Dimensions of the experimental specimen(unit：mm)

榫头尺寸/mm 长 高 宽 枋尺寸/mm 长 高 宽 柱尺寸/mm 柱径 柱长 1401204070012080140800

表2 木材力学性质

注：ER表示横纹(径向)抗压弹性模量；EL表示顺纹抗压弹性模量；νLR表示径向相对于顺纹方向的泊松比.

McKenzie和Karpovich的研究表明对于种类不同、粗糙度不同以及相对速率不同的木材，其间的滑动摩擦系数值在0.1～0.65区间内[12].本文选取摩擦系数0.35，并根据表2中的材性数据，可以得到落叶松横纹径向受压屈服时的应变为1.34%，由式(4)计算可得：

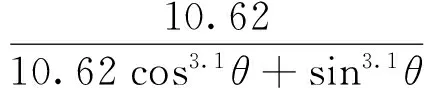
(17)

分别将理论计算和试验得到弯矩-转角曲线绘于图9.

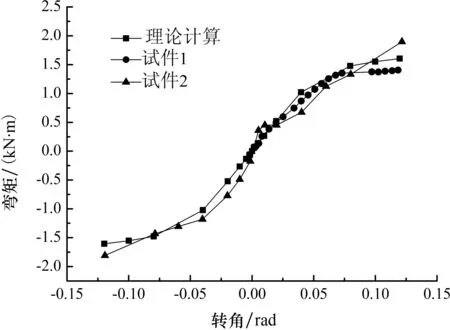
图9 转动弯矩-转角的理论计算结果与试验结果对比Fig.9 Comparison between theoretical and experimental results on the moment-rotation

从图9可以看出：当荷载小于屈服值时，曲线变化趋势基本相同，转动弯矩随转角的增加迅速增大；然而，随着转角增大，木材进入塑性阶段，曲线都表现出了明显的塑性特征，转动弯矩-转角曲线的斜率开始迅速递减，而弯矩随转角的增加则上升缓慢.由于试验所用木材不可避免地存在初始物理缺陷，且容易受到各种环境因素的影响，使木材力学性能有一定程度的离散，从而导致计算曲线与试验曲线存在一定差异，但从整体来看，两曲线的总体变化趋势、曲线斜率等基本吻合，误差较小，能够合理地反映单向直榫节点在转动过程中的弯矩变化情况.

4 单向直榫节点转动弯矩-转角影响因素分析

经过理论分析和试验结果的对比，发现影响单向直榫节点转动弯矩-转角关系的因素主要为材料类型及榫头尺寸等.因此，本文以文献[11]中的试件为研究对象，分别选取摩擦系数、榫头长度和榫头宽度3个主要因素进行分析.

4.1 木材间摩擦系数的影响

不同的木材其接触面的纹理不同，因而摩擦系数也不相同，会直接影响节点的转动刚度.取不同摩擦系数μ(0.25，0.35，0.45和0.55)，分析其对单向直榫节点转动弯矩和转动刚度的影响，计算结果如图10所示.可以看出，增大摩擦系数可以提高单向直榫节点的转动弯矩，但提高幅度不大，而且对节点的初始刚度几乎没有影响.

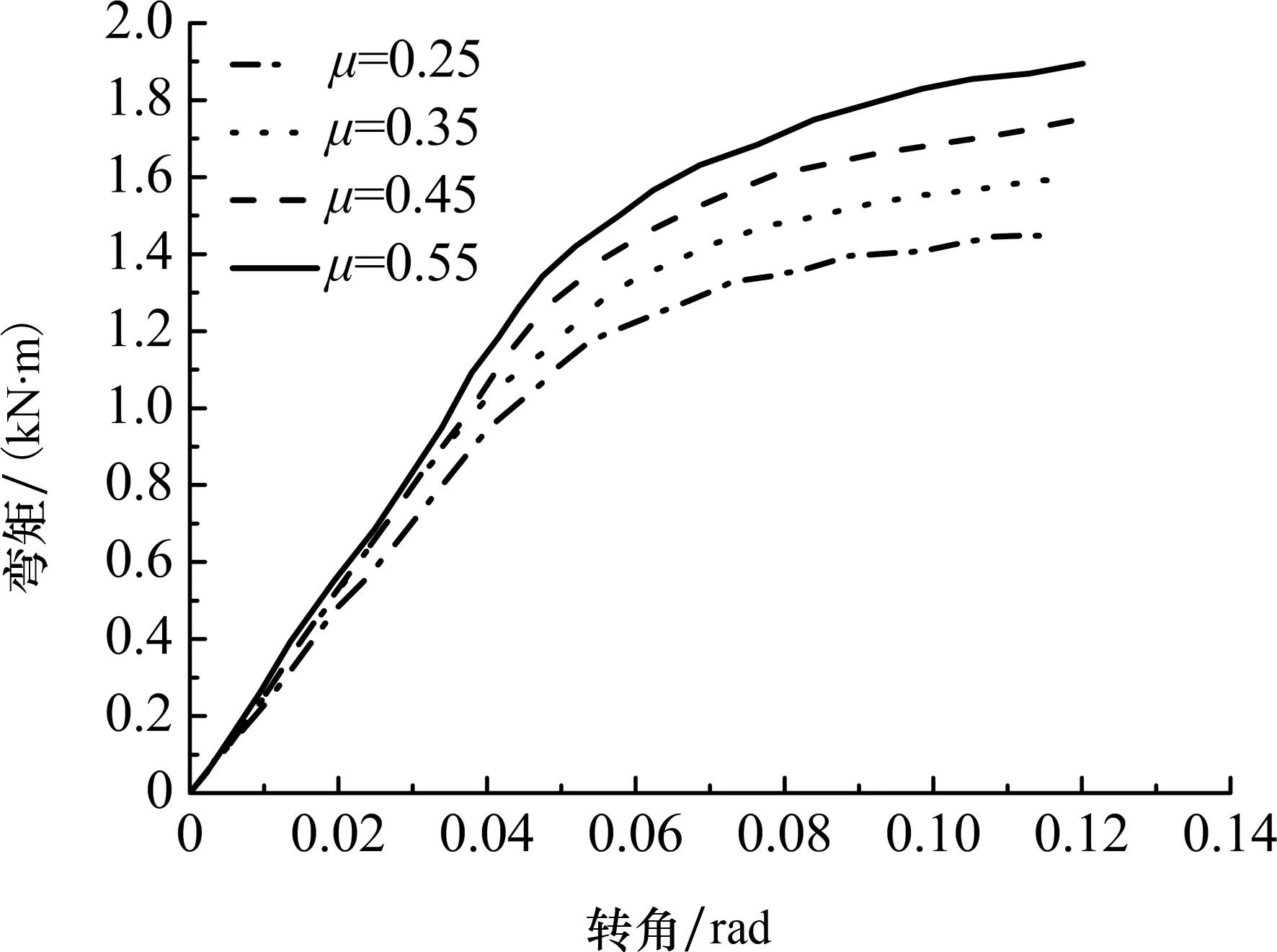
图10 不同摩擦系数单向直榫节点的转动弯矩-转角曲线Fig.10 Moment-rotation curves of the straight mortise-tenon joint at different friction coefficients of wood

4.2 榫头长度的影响

榫头长度的变化会引起榫卯接触挤压区域长度的变化，进而影响节点转动刚度.通过变换榫头长度l(80 mm，100 mm，120 mm和140 mm)，分析不同榫头长度的影响程度，计算结果如图11所示.可以看出，当榫头长度与柱径之比小于1时，虽然随着榫头长度的增加，柱子的截面不断削弱，但其转动弯矩和初始转动刚度都显著提高.

图11 不同榫头长度单向直榫节点的转动弯矩-转角曲线Fig.11 Moment-rotation curves of the straight mortise-tenon joint at different lengths of the tenon

4.3 榫头宽度的影响

榫头宽度的变化会引起榫卯接触挤压区域宽度的变化，从而影响节点转动刚度.通过变换榫头宽度bs(30 mm，40 mm，50 mm和60 mm)，分析不同榫头长度对单向直榫节点的影响，计算结果如图12所示.可以看出，在一定范围内增大榫头宽度不仅可以提高节点的转动弯矩，而且可以提高初始刚度.

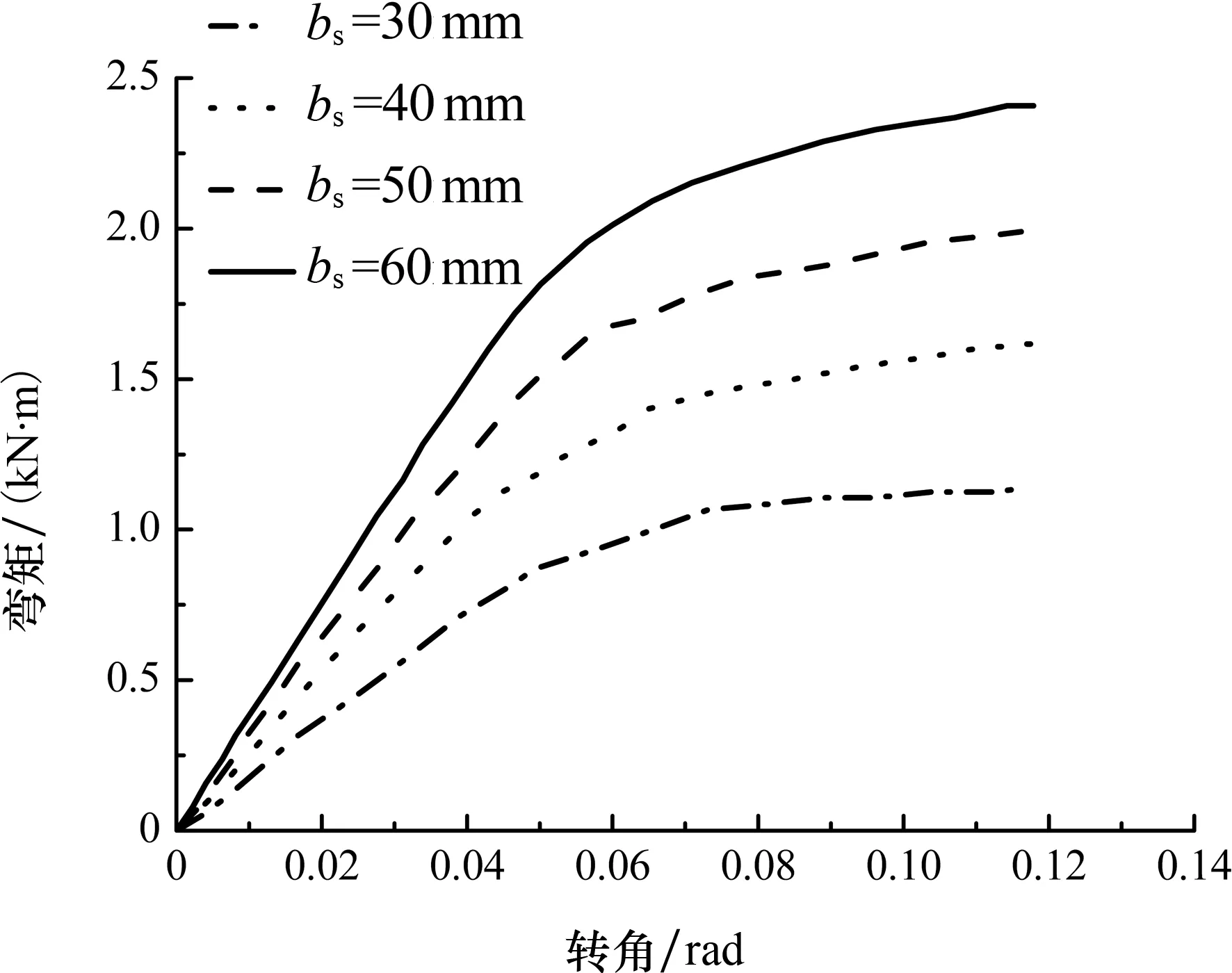
图12 不同榫头宽度单向直榫节点的弯矩-转角曲线Fig.12 Moment-rotation curves of the straight mortise-tenon joint at different widths of the tenon

5 结 论

本文分析了单向直榫节点的受力机理，对其节点的弯矩-转角理论公式进行了推导，并对影响单向直榫节点弯矩-转角关系的主要参数进行了分析，得到以下主要结论：

1)理论推导得到的单向直榫榫卯节点的弯矩-转角关系方程，与已有试验结果吻合较好，可为传统木结构的研究提供一定的参考.

2)影响单向直榫节点弯矩-转角关系的最主要因素是榫头长度，当榫头长度与柱径之比小于1时，随着榫头长度的增加,单向直榫节点的转动弯矩和初始转动刚度显著提高；摩擦系数的增大可以在一定程度上提高单向直榫节点的转动弯矩，但对节点的初始刚度几乎没有影响.

[1] 马炳坚.中国古建筑木作营造技术[M].2版.北京:科学出版社，2003:119-132.

MA Bingjian.Building techniques on Chinese ancient wood structure[M].2nd ed.Beijing：Science Press，2003:119-132.(In Chinese)

ZHAO Hongtie，XUE Jianyang，SUI Yan，etal.Chinese ancient wooden building and seismic：test，theory and reinforcement method[M].Beijing：Science Press，2012：103-112.(In Chinese)

[3] 潘毅，李玲姣，王慧琴，等.木结构古建筑震后破坏状态评估方法研究[J].湖南大学学报:自然科学版，2016，43(1)：132-142.

PAN Yi，LI Lingjiao，WANG Huiqin，etal.Research on evaluation methods for post-earthquake damage state of ancient wooden buildings [J].Journal of Hunan University： Natural Sciences，2016,43(1):132-142.(In Chinese)

[4] KISHI N，CHEN W F.Moment-rotation relations of semi-rigid connections with angles [J].Journal of Structure Engineering，1990，116(7)：1813-1834.

[5] 赵鸿铁，张海彦，薛建阳，等.古建筑木结构燕尾榫节点刚度分析[J].西安建筑科技大学学报:自然科学版，2009，41(4)：450-454.

ZHAO Hongtie，ZHANG Haiyan，XUE Jianyang，etal.Stiffness analysis of dovetail joints for ancient timber structure building [J].Journal of Xi’an University of Architecture and Technology：Natural Science 2009，41(4)：450-454.(In Chinese)

[6] 杨艳华,王俊鑫,徐彬.古木建筑榫卯连接M-θ相关曲线模型研究[J].昆明理工大学学报:理工版，2009，34(1)：72-76.

YANG Yanhua，WANG Junxin，XU Bin.Research of interaction curves model of mortise-tenon joint in historic timber buildings [J].Journal of Kunming University of Science and Technology：Natural Science，2009，34(1)：72-76.(In Chinese)

[7] 谢启芳，杜彬，张风亮，等.古建筑木结构燕尾榫节点弯矩-转角关系理论分析[J].工程力学，2014，31(12)：140-146.

XIE Qifang，DU Bin，ZHANG Fengliang，etal.Theoretical analysis on moment-rotation relationship of dovetail joints for Chinese ancient timber structure building[J].Engineering Mechanics,2014，31(12)：140-146.(In Chinese)

[8] 潘毅，王超，唐丽娜，等.古建筑木结构直榫节点力学模型的研究[J].工程力学，2015，32(2)：82-89.

PAN Yi，WANG Chao，TANG Lina，etal.Study on mechanical model of straight-tenon joints in ancient timber structures[J].Engineering Mechanics，2015，32(2)：82-89.(In Chinese)

[9] 陈春超，邱洪兴，包轶男.瓜柱柱脚直榫节点受弯力学模型研究[J].湖南大学学报:自然科学版,2015,42(3):50-56.

CHEN Chunchao，QIU Hongxing，BAO Yinan.Study on the flexural mechanical model of straight mortise-tenon joints in the base of melon-column [J].Journal of Hunan University：Natural Sciences，2015,42(3):50-56.(In Chinese)

[10]CHANG W S，HSU M F，KOMATSU K.Rotational performance of traditional Nuki joints with gap II：the behavior of butted Nuki joint and its comparison with continuous Nuki joint [J].Journal of Wood Science，2007，52(5)：401-407.

[11]谢启芳，郑培君，崔雅珍，等.古建筑木结构直榫节点抗震性能试验研究[J].地震工程与工程震动，2015，35(3)：232-241.

XIE Qifang，ZHENG Peijun，CUI Yazhen，etal.Experimental study on seismic behavior of straight mortise-tenon joints of ancient timber buildings [J].Earthquake Engineering and Engineering Dynamics，2015，35(3)：232 -241.(In Chinese)

[12]MCKENAIE W M,KAPOVICH H.The frictional behavior of wood[J].Wood Science and Technology,1968,2(2):139-152.

Theoretical Analysis on Moment-rotation Relationship of StraightMortise-tenon Joints for Chinese Traditional Wooden Buildings

XIE Qifang1†，WANG Long1，ZHENG Peijun2，ZHANG Lipeng1，QIAN Chunyu3

(1.School of Civil Engineering，Xi’an University of Architecture & Technology，Xi’an 710055，China;2.China Construction Seventh Engineering Division Co，Ltd，Zhengzhou 450004,China;3.China Jikan Research Institute of Engineering Investigations and Design Co，Ltd，Xi’an 710043，China)

The force mechanism was analyzed and the moment-rotation calculation formulas were deduced for the straight mortise-tenon joints.Good agreement between the predictions and test results was observed.Based on the moment-rotation calculation formulas,the factors affecting the rotational stiffness of the straight mortise-tenon joints were analyzed.The results show that:the rotational moment and initial rotational stiffness are increased significantly with the increase of the length of a tenon when the ratio of the length to the column diameter is less than 1;the rotational moment and initial rotational stiffness are also improved with the increase of the width of a tenon;the rotation moment of the joint is increased to a certain extent with the increase of the friction coefficients,but the initial rotational stiffness is affected little.The conclusins are helpful in the seismic performance assessment and reinforcement of the traditional wooden buildings.

traditional wooden structures;straight mortise-tenon joints;force mechanism;moment-rotation relationship;theoretical analysis

1674-2974(2017)07-0111-07

10.16339/j.cnki.hdxbzkb.2017.07.014

2016-04-04

国家自然科学基金资助项目(51278399),National Natural Science Foundation of China(51278399);陕西省自然科学基础研究计划重大基础研究项目(2016ZDJC-23),Natural Science Foundation Project of Shaanxi Province(2016ZDJC-23);国机集团科技发展基金资助项目(13-192),Science and Technology Development Foundation of China National Machinery Industry Corporation(13-192);西安建筑科技大学创新团队资助计划项目,Xi’an University of Architecture and Technology Innovation Group Project

谢启芳(1978-)，男，江西赣州人，西安建筑科技大学副教授，工学博士†通讯联系人，E-mail:nacy.xie@163.com

TU366.2

A