基于滑移线场理论的临坡地基承载力简化分析方法*

胡卫东，曹文贵

(1.湖南大学 岩土工程研究所，湖南 长沙 410082；2.湖南理工学院 土木建筑工程学院，湖南 岳阳 414000)

基于滑移线场理论的临坡地基承载力简化分析方法*

胡卫东1, 2†，曹文贵1

(1.湖南大学 岩土工程研究所，湖南 长沙 410082；2.湖南理工学院 土木建筑工程学院，湖南 岳阳 414000)

在现有相关研究基础上，探讨了无重土平地基Hill破坏模型及其承载力滑移线解和斜坡地基Hill破坏模型及其承载力滑移线解，提出临坡条形基础地基破坏模式应是介于平地基破坏模式和斜坡地基破坏模式两种临界状态之间的一种连续变化模式，在相同边界条件下，改变坡顶距的临坡地基极限承载力滑移线解答则是介于这两种地基状态间的一个连续函数解，并据此构建出临坡条形基础无重土地基的双侧不对称Hill滑动破坏模式.在此研究基础上，通过引入宽度比系数将基底分为两个均布受压区，采用“等代自由面”简化边坡面上滑块的应力影响作用，使临坡一侧受压区极限压力可直接用已有斜坡地基滑移线解表示.通过分析宽度比系数、坡顶距和破坏模式之间的关系，设定了宽度比系数函数，建立出基于滑移线场理论的临坡地基极限承载力确定方法.通过与现有研究成果的对比分析，表明了本文研究方法的可行性与合理性.

临坡地基；条形基础；承载力；滑移线；Hill破坏模式

随着临坡地基广泛应用在各类岩土工程结构中，临坡地基承载力研究已成为这一领域的研究热点.近年来，不少学者采用极限平衡法、滑移线法、极限分析法及数值分析法[1-8]等方法对临坡地基破坏模式和承载能力进行深入研究，使得临坡地基承载力理论研究取得了长足的进步.

理论研究表明，基础距坡顶距离、坡角、土体力学性质、基础型式、基础宽度及基础埋深等因素对临坡地基破坏模式和承载能力都有着一定影响，特别是基础距坡顶距离的不同，将显著影响和改变临坡地基的破坏模式，使水平地基、临坡地基、斜坡地基在破坏模式和承载力分析方法上存在明显区别，其承载能力自然也有较大差异.基础距坡顶距离这一关键因素如何影响临坡地基破坏模式和承载能力正是本文研究的重点内容.

考虑基础距坡顶距离的不同，现有临坡地基承载力研究普遍采用单侧滑动和双侧滑动两种破坏模式.已有的采用单侧滑动破坏的研究成果：如Mizuno[9]等将基底下土体分为3个破坏区域，利用极限静力平衡法进行分析研究；Kusakabe等[10]根据极限分析上限法求解坡顶作用垂直荷载的地基承载力；Castelli等[11]建立了圆弧状滑动破坏面，利用极限平衡方法求解静力和动力荷载下的地基极限承载力；杨峰等[12]、赵炼恒等[13]基于极限分析理论有效考虑了单侧多滑块组合破坏机构的滑块速度和变形协调相容问题.在基础距坡顶距离不为零时，采用单侧滑动破坏模式的计算方法往往偏于安全和保守，但单侧滑动破坏模式无法准确反映不同临坡距离情况下地基的变形机制和破坏形态，也难以正确反映由于坡顶距离不同而导致的破坏模式的变化和不对称性.另外一种采用双侧非对称破坏模式进行临坡地基承载能力分析研究：如Swami等[1]提出用土体抗剪强度系数来分析坡后土体的受力情况，并利用极限平衡分析方法和极限分析上限法进行临坡地基承载力的比较，但对于基础距坡顶距离如何影响临坡地基破坏模式和地基承载力并没有进行深入分析；Graham等[14]基于滑移线场理论建立了临近无黏性土坡地基的非对称双侧破坏模式，并提出随着坡顶距离变化破坏模型尺寸和基底楔体尺寸呈线性变化，提出了相应的几何破坏模式确定方法，但其方法未能适用黏性土地基；胡卫东等[15]基于刚体极限平衡理论建立了双侧非对称模式下临坡地基极限承载力确定方法，通过对多个角度变量进行优化计算来反映坡顶距离不同时破坏模型的变化，但仍未能准确表达基础距坡顶距离的影响作用.基于以上分析可知，采用双侧非对称破坏模式更有利于反映基础距坡顶距离对临坡地基破坏模式的影响，但现有研究建立基础距坡顶距离与临坡地基破坏模式及承载力间的准确关系仍存在很大不足，有待进一步深入研究.

综合上面所述，本文将从临坡条形基础地基非对称破坏模式研究入手，分析探讨无重土平地基Hill破坏模型及其承载力滑移线解和斜坡地基Hill破坏模型及其承载力滑移线解，利用已有研究承载力滑移线解的成果，建立考虑基础距坡顶距离影响和非对称性特点的临坡地基合理破坏模式，基于滑移线场理论建立临坡地基承载力简化分析模型与方法，以期完善临坡地基承载力分析的理论与方法.

1 临坡地基破坏机理与破坏模式

利用滑移线解法可以求得松散介质极限平衡状态的应力场、变形速度场及相应极限荷载，是一种建立在严格极限平衡理论基础上的精确解法，但是只有在很简单的情况下能获得精确解答，一般情况需采用数值方法得到近似解[16].为了避免繁杂的数值计算,建立基于滑移线场理论临坡地基极限承载力分析方法，利用已有研究地基极限承载力滑移线精确解答是一种很好的途径，考虑到地基极限承载力的滑移线精确解通常都应用于无重土地基上，本文首先考虑无重土地基进行深入研究，提出一种新的临坡地基极限承载力简化分析方法.为此，先作如下基本假定：

1)地基材料为无重的理想刚塑性体，地基发生剪切破坏形成连续滑动面；

2)临坡条形基础地基承载力问题可视为平面问题；

3)滑动区域内土体在达到塑性极限平衡状态时服从Mohr-Coulomb屈服准则和相关联流动法则；

4)基础表面光滑，即基底摩擦力为零.

1.1 平地基Hill破坏机制及其承载力滑移线解

平地基光滑条形基础Hill机构为对称破坏机构，可以看作临坡地基当中条形基础距坡顶距离较大时，地基变形和破坏不受坡顶距离影响的一种临界状态破坏模式，如图1所示.基底刚性三角形楔体具有相同底角α1=π/4+φ/2，对数螺线区的中心角θ0相同，均为π/2，被动区刚性楔体有相同底角α2=π/4-φ/2.

图1 平地基条形基础地基Hill破坏模式Fig.1 The failure mechanism for strip footing

Hill破坏机构其对应滑移线场、速度场如图2所示，图左半部分为Hill对称破坏机构的滑移线场，其中Ⅳ区和Ⅵ区为均匀应力场，介质内滑移线场是两簇直线，Ⅴ区为简单应力场，其α滑移线为直线，β滑移线为对数螺线；右半部分表示其相应容许速度场.

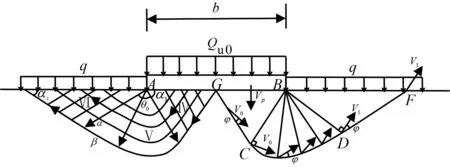
图2 平地基Hill机构滑移线场与速度场Fig.2 Corresponding slip-line field and velocity field for the Hill failure mechanism

根据已有研究成果，平地基无重土条形基础Hill破坏机构的滑移线解与极限分析上限解一致[17].其平地基无重土的极限承载力滑移线解也一直被认为是严格解，表示为：

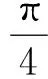
ccotφ=qNq0+cNc0

(1)

式中：φ为地基土内摩擦角；c为地基土黏聚力；q为条形基础两侧埋深内土的影响作用，其大小可表示为：

q=γD

(2)

其中：γ为土体重度；D为基础埋深.Nq0，Nc0为平地基承载力影响系数，可表示为：

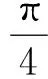
(3)

Nc0=(Nq0-1)cotφ

(4)

地基影响破坏区域为条形基础两侧L0范围.L0的大小可表示为：

(5)

1.2 斜坡地基Hill破坏机制及其承载力滑移线解

基础作用在坡顶边缘，距坡顶距离为0的临坡地基，即斜坡地基，可以看作临坡地基当中受距离影响和承载力减损最大的又一种临界状态破坏模式，条形基础地基在竖直均布荷载作用下斜向下运动，临坡地基破坏模式蜕化为斜坡地基单侧滑动Hill破坏模式，如图3所示.基础埋深内的影响可以考虑为斜坡上作用的均布垂直荷载q，基础以下滑动破坏区域可划分为主动区Ⅰ，过渡区Ⅱ和被动区Ⅲ，其中α1=π/4+φ/2，μ=π/4-φ/2，θ1=π/2-η.

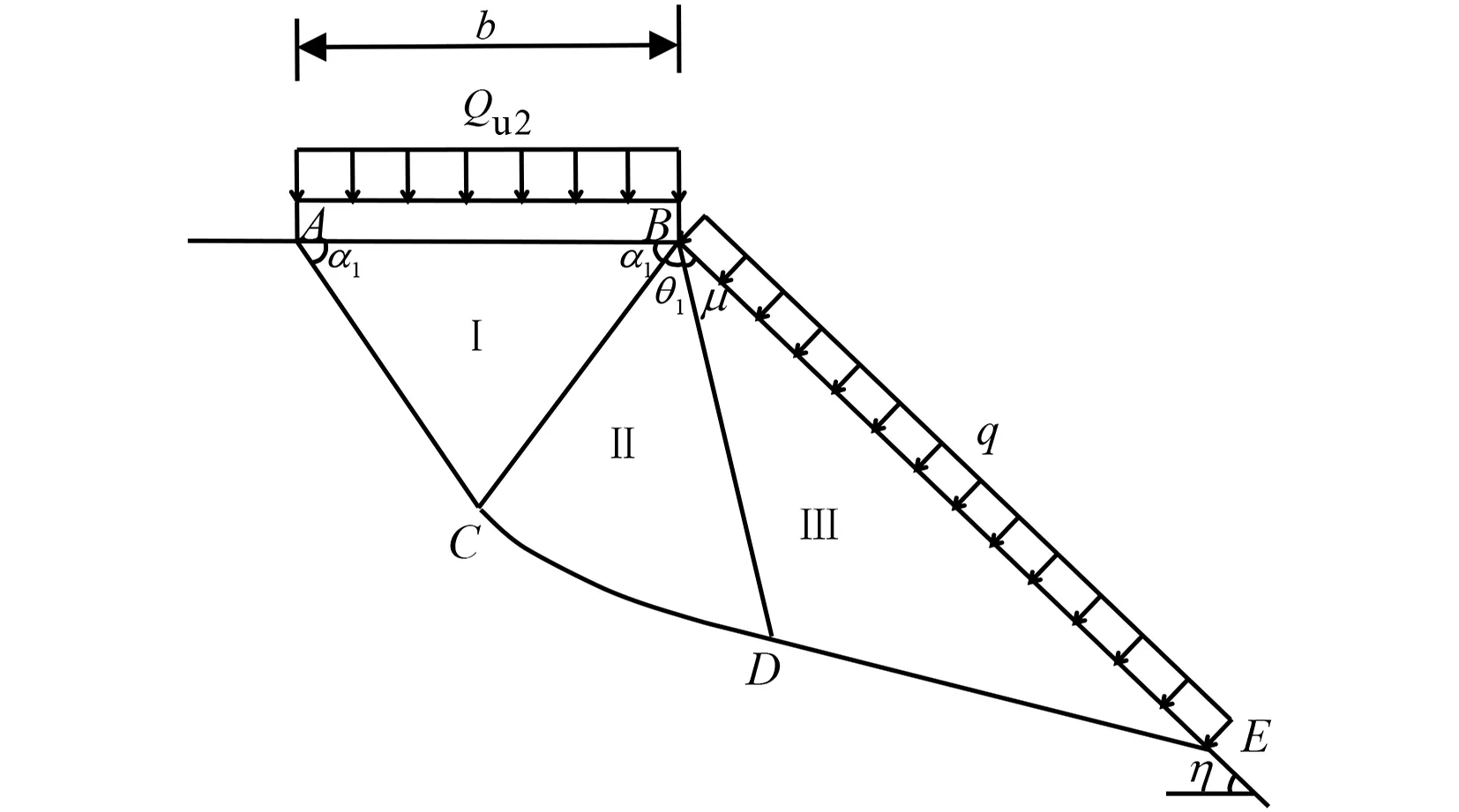
图3 斜坡地基(边坡距为0)破坏模式Fig.3 The failure mechanism for strip footing near slope

条形基础斜坡地基的滑移线场及相应容许速度场如图4所示.图4(a)中Ⅰ区和Ⅲ区为均匀应力场，其α及β滑移线均为直线；Ⅱ区为简单应力场，其α滑移线为直线，β滑移线为对数螺线.

图4 斜坡地基(边坡距为0)滑移线场与速度场Fig.4 Corresponding slip-line field and velocity field for the failure mechanism

根据已有研究，条形基础无重土斜坡地基相应极限承载力滑移线解与极限分析上限解相同[18]，其极限承载力滑移线解为严格解，表示为：

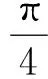
(6)

式中：η为斜坡坡角；Nq2，Nc2为斜坡地基承载力影响系数，可分别表示为：

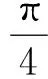
(7)

Nc2=(Nq2-1)cotφ

(8)

1.3 临坡地基的Hill破坏模式

前面已探讨了无重土条形基础平地基和斜坡地基Hill机构的破坏模式及其极限承载力滑移线解，这两种地基的破坏模式为临坡地基的两种临界状态破坏模式.当坡角η一定，基础距坡顶距离为0时，临坡地基破坏模式蜕化为斜坡地基破坏模式，即单侧滑动破坏模式；坡角η保持不变,当基础距坡顶距离大于L0时，临坡地基破坏模式蜕化为平地基破坏模式，即双侧对称破坏模式.于是，在相同坡角情况下，基础距坡顶距离∈(0,L0)之间的临坡地基破坏模式应是介于平地基和斜坡地基两种临界状态破坏模式之间的一种连续变化状态，即双侧非对称破坏模式.因此，对于新构建的临坡条形基础地基破坏模式，须同时满足下面两个条件：①基础距坡顶距离变化时破坏模式是可以连续变化的；②基础距坡顶距离为0或者大于L0时，破坏模式能蜕化为斜坡地基或平地基破坏模式.

根据松散介质滑移线场理论构建临坡条形基础地基Hill破坏机构[19]，将破坏机构划分为7个滑块或分区，如图5所示，具体分析情况如下：

1)受边坡存在的影响，临坡条形基础地基Hill破坏机构为双侧非对称破坏模式，地基土向两侧均发生剪切滑动破坏，整个滑动破坏区域大小及形状呈现明显不对称性.

2)临近边坡一侧滑动破坏区域可划分为主动区Ⅰ、塑性剪切区Ⅱ、被动区Ⅲ和松动区Ⅳ.随着基础至坡顶距离L1由L0不断减小至0，三角形滑块Ⅰ两个底角α1=π/4+φ/2不变，基底长度b1由b/2不断增大至b，破坏区域的大小也相应增大；对数螺线区滑块Ⅱ，中心角θr≤π/2；滑块Ⅲ的两个三角形底角μ=π/4-φ/2；滑块Ⅳ随着坡顶距不断减小，开始出现并不断增大至最后消失，β角自0°不断增大至η.根据滑移线场理论可知，作用均布压力q的BF和EF边界及作用均布极限压力Qur的GB基底面均会形成不同的两簇直线滑移线，滑块Ⅲ与Ⅳ组成的BDEF区域和滑块Ⅰ所在GBC区域为均匀应力场；夹在两个均匀应力场中间的滑块Ⅱ则形成简单应力场，其中α应力滑移线为直线并相交于中心点B点，β应力滑移线为对数螺线.

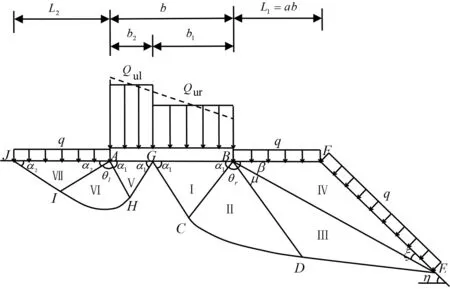
图5 临坡条形基础地基破坏模式Fig.5 The failure mechanism for strip footing near slope

3)条形基础内侧地基滑动破坏区域与平地基Hill机构左半部分破坏模型一致，可划分为主动区Ⅴ、塑性剪切区Ⅵ、被动区Ⅶ.随着坡顶距L1由L0不断减小至0，三角形滑块Ⅴ基底长度b2由b/2不断减小至0，破坏区域的大小也相应减小.同样，根据滑移线场理论，作用均布压力q的边界AJ和作用均布极限压力Qul的基底面GA均会形成不同的两簇直线滑移线，即滑块Ⅴ和滑块Ⅶ内为均匀应力场，夹在两个均匀应力场中间的滑块Ⅵ则形成简单应力场.

基础外侧边缘至坡顶距离L1可以用距离比系数a来表示，设条形基础宽度为b，则有L1=ab.当坡角η一定，a=0时，破坏模式蜕化为斜坡地基破坏模式；当坡角η一定，a=L0/b时，破坏模式蜕化为平地基破坏模式.

上述多滑块破坏模式即构成临坡条形基础地基双侧非对称Hill机构破坏模式，是介于两种临界状态间连续变化的破坏模型，下面将在此基础上探讨其极限承载力的滑移线求解方法.

2 临坡地基极限承载力的滑移线求解方法

综合上面的分析，坡顶距离变化时L1∈(0,L0)，条形基础临坡地基双侧非对称破坏模式介于平地基和斜坡地基两种临界状态之间，并且是连续变化的.考察这两种临界状态破坏模式的极限承载力滑移线解，即式(1)和式(6)，其解答式具有很大相似性和连续性，基于此，在相同地基与边界条件下，平地基的滑移线解为最大值，斜坡地基滑移线解为最小值，改变坡顶距L1∈(0,L0)的临坡地基极限承载力的滑移线解则是介于平地基和斜坡地基滑移线解的一个连续函数解.

为了计算方便，基底连续分布极限压力可以简化为两个大小不同均布受压区(图5)，当坡顶距L1由L0不断减小至0，临坡一侧地基的应力场和速度场发生很大变化，其破坏模式由平地基破坏模式发展为斜坡地基破坏模式，极限承载力减损也逐步增大，与此相应滑块Ⅰ基底极限压力Qur的大小由平地基破坏状态的Qu0逐渐减小至斜坡地基破坏状态的Qu2.同时坡顶距变小，滑块Ⅴ的大小虽然受到影响，但内侧地基Hill机构几何模型形式依然保持平地基对称的Hill机构模型形式，这一侧的应力滑移线场和相容速度场的分布形式也没有变化，因此，滑块Ⅴ基底极限压力Qul的大小保持不变，其值仍为平地基极限承载力值Qu0.于是临坡地基极限承载力可表示为：

Qu=(b1Qur+b2Qul)/b

(9)

条形基础基底两个均布受压区的宽度可以用宽度比系数g来表示：

b1=gb

(10)

b2=(1-g)b

(11)

于是，临坡一侧极限压力Qur的确定就成为本文临坡条形基础地基极限承载力研究的关键问题，为了简化分析，首先引入“等代自由面”来处理和计算滑块Ⅳ的应力作用.

2.1 “等代自由面”简化方法

为了简化分析，对于临坡条形基础地基，取滑块Ⅳ(即BEF)为隔离体进行受力分析，如图6所示，在基础一侧坡顶面BF和斜坡面EF上作用有均匀分布的超载q；“等代自由面”BE面上作用有法向分布应力σ0和切向分布剪应力τ0，并假设应力σ0和τ0为均匀分布；于是，水平面BF和斜坡面EF上作用的均匀分布的q可由滑动平面BE上的等代应力σ0和τ0来代替，这样，就可以将滑块体BEF移去，用“等代自由面”BE面来代替[20].

图6 滑块Ⅳ受力分析图Fig.6 Static analysis for the slider body Ⅳ diagram

设定滑动BE面与水平面的夹角为β，β可看作是与坡顶距和坡角有关的参数.于是，根据BE面在法线方向和切线方向上的静力平衡条件可分别得到：

(12)

(13)

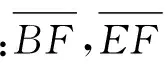
ξ=η-β

(14)

根据三角形BEF中正弦关系有

(15)

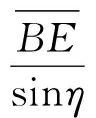
(16)

将式(15)代入式(12)和(13)，可得“等代自由面”上法向分布应力σ0和切向分布剪应力τ0，其大小分别表示为：

τ0=0

(17)

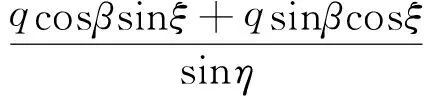
(18)

由式(17)和式(18)可知，“等代自由面”BD面上没有切向均布应力，只有法向均布应力q，经过化简之后的等代BD面相当于斜坡地基的斜坡面，于是，临坡一侧地基极限承载力即可由斜坡地基极限承载力解来表示：

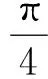
ccotφ

(19)

化简之后的临坡一侧地基极限承载力相应于坡角为β的斜坡地基极限承载力，随着临坡距L1由L0减小至0，β其大小则逐渐由0增大至η.

由于BD滑动面上土体处于塑性极限平衡状态，假设BD面上作用有法向均布应力σb和切向均布应力τb，BD面上应力即对应摩尔应力圆中d点坐标应力；BE面上的分布应力σ0和τ0则对应摩尔应力圆中e点坐标应力；应力圆中的bd线与be线形成的夹角∠dbe为BD面与BE面夹角μ的2倍，∠dbe=2μ=π/2-φ，如图7所示.

图7 极限平衡状态下的摩尔应力圆Fig.7 Limit equilibrium Mohr stress circle

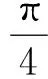
(20)

2.2 临坡地基极限承载力求解

根据三角形BDE中正弦关系有：

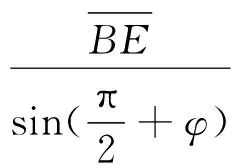
(21)

(22)

将式(22)和式(21)代入式(16)，可得

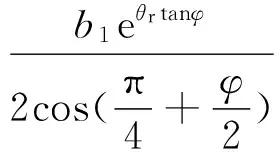
(23)

于是，上式可以写成

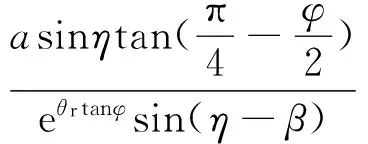
(24)

式中：对数螺线区中心角θr=π/2-β.

坡顶距L1由L0减小至0，距离比系数a自初始坡顶距a0减小至0，a0可表示为：

(25)

相应地，宽度比系数g则从0.5增大至1.0，如图8所示.图8中横坐标a在[0,a0]区间上，g的函数应为单调递减连续函数，同时还需满足边界要求.

a=0,β=η,g=1

(26)

a=a0,β=0,g=0.5

(27)

为简化计算，将g的函数表示为线性函数：

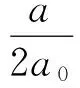
(28)

显然，式(28)满足边界要求即式(26)和(27).将式(28)代入式(24)，通过迭代的方法即可确定不同坡顶距对应的β，于是可得到对应临坡一侧地基的极限承载力Qur.将式(10)和式(11)代入式(9)，可得：

Qu=gQur+(1-g)Qul

(29)

总极限承载力Qu亦可写成：

Qu=qNq+cNc

(30)

式中：

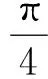
(31)

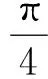
(1-g)]-cotφ

(32)

即

Nc=(Nq-1)cotφ

(33)

图8 宽度比系数g与距离比系数a的关系图Fig.8 The diagram of width ratio coefficient with distance ratio coefficient

2.3 有重土临坡地基极限承载力求解

有重土基础下的地基滑移线网发生较大变化，主动区两族滑移线及塑性剪切区射线滑移线都变成了曲线[21]，地基的极限荷载也有了相应变化，然而，由于目前还没有重土地基的极限荷载的解析解，为了计算有重土地基的极限承载力，一般可以将无重土，即γ=0，φ≠0，而c≠0,q≠0的地基极限承载力与有重土，即γ≠0，φ≠0，而c=0,q=0的地基极限承载力线性叠加而得到.故临坡地基极限承载力式(30)即可写成：

(34)

式中：Nγ表示自重引起的地基承载力系数，可采用极限平衡法、上限法和滑移线场数值解法等计算分析方法近似确定.本文采用Hensen滑移线法数值计算结果进行简化得到的Nγ计算式为：

Nγ=1.8(Nq-1)tanφ

(35)

3 验证与对比分析

3.1 理论计算与比较

为了验证本文提出的分析模型与求解方法的正确性与合理性，与已有试验数据及理论研究方法进行有效比较，对于无黏性土地基，将式(34)转化成下式：

(36)

(37)

根据计算所得无黏性临坡地基承载力系数Nγq与Shields等[22]的大尺寸试验结果、Graham等[14]的理论解及文献[23]的计算结果进行比较，如表1所示.表1中，内摩擦角采用三轴试验测得的抗剪强度指标，压密砂土内摩擦角φtx=37°，密实砂土内摩擦角φtx=41°.通过比较分析，可以得到以下结论.

表1 本文方法与Shields试验结果、Graham理论解及文献[23]的Nγq比较Tab.1 Comparison of calculated with experiment and theoretical values ofNγq

注：*考虑平面应变影响因素的数值模拟结果(φ=1.1φtx)，φtx为三轴试验测得的抗剪强度指标.

1)本文计算压密砂土结果与Shields的大尺寸试验结果较接近，而对于密实砂土，利用平面应变与三轴试验换算关系得到内摩擦角φ=1.1φtx进行求解，计算结果与Shields试验结果较接近，这也验证了本文方法的正确性.虽然存在一定误差，但这与模型试验尺寸效应和力学参数选取有关系，也是难以避免的.

2)本文计算压密砂土和密实砂土结果与文献[23]采用数值模拟计算结果大部分较为接近，并且与其他方法数据结果的总体趋势是一致的，这也说明了本文方法的合理性与可行性.

3)相比Graham的理论解，本文方法计算结果更接近于试验结果，这与本文采用承载力线性叠加得到临坡地基极限承载力滑移线解有着一定关系，而且，文中采用Hensen方法简化Nγ值偏于保守.

3.2 工程实例

某临坡条形基础地基中基础两侧埋深相同D=1 m，基础宽度b=2 m，c=10 kPa，φ=30°，γ=18 kN/m3，按边坡坡角η=30°，基础外侧边缘距坡顶距离与基础宽度之比a=1～a0，进行计算.采用本文方法及文献[23]方法进行比较分析，计算分析结果见表2.

由表2可知，距离比系数a对临坡地基承载力影响较大，一般来说，随着坡顶距的增大，边坡对地基承载力的影响会不断减小，临坡地基承载力逐渐增大并收敛于平地地基时的承载力值.如表2所示，文献[23]方法以a=4为控制上限得到最终极限承载力Qu=1 020.04 kPa，本文方法以a=a0时收敛与平地地基破坏模式，得到极限承载力Qu=958.12 kPa，两种方法计算结果随坡顶距离变化规律一致，且最终收敛于平地地基的极限承载力值差距较小，这也进一步表明本文方法的可行性与适用性.

表2 坡顶距离比变化时地基极限承载力计算值(η=30°)

Tab.2 Calculated values of ultimate bearing capacityfor various footing locations(η=30°)

4 结 语

1)本文利用已有研究无重土平地基和斜坡地基破坏模型及其承载力滑移线解，提出临坡条形基础地基破坏模式应是介于平地基破坏模式和斜坡地基破坏模式两种临界状态之间的一种连续变化模式，构建出考虑基础距坡顶距离影响和非对称性特点的临坡地基合理破坏模式，为临坡地基承载力确定奠定了坚实的理论基础.

2)引入滑移线场理论进行分析，临坡地基极限承载力滑移线解是介于平地基和斜坡地基滑移线解后的一个连续函数解，利用“等代自由面”简化边坡面上滑块的应力影响作用，通过设定宽度比系数函数，建立出临坡地基极限承载力分析模型及计算方法.

3)结合工程算例，通过与大型试验数据及其他理论方法和数值分析方法计算结果进行对比分析，验证了本文基于滑移线场理论的临坡地基极限承载力的简化计算方法的可行性与合理性.

[1] SWAMI S, SUD V K,HANDA S C.Bearing capacity of footings adjacent to slopes[J].Journal of Geotechnical Engineering, ASCE, 1989, 115(4):553-573.

[2] CHEN W F.Limit analysis and soil plasticity[M].Amsterdam:Elsevier, 1975:1-60.

[3] 胡卫东,曹文贵.基于非对称破坏模式的临坡地基承载力上限极限分析方法[J].中国公路学报,2014,27(6):1-9.

HU Weidong,CAO Wengui.Upper limit analysis method for ultimate bearing capacity of ground foundation adjacent to slope based on asymmetry failure mode[J].China Journal of Highway and Transport, 2014,27(6):1-9.(In Chinese)

[4] MARTIN C M.Exact bearing capacity calculations using the method of characteristics[C]// Proceedings of the 11th International Conference of IACMAG.Turin: World Scientific Publishing Company, 2005, 4:441-450.

[5] KUMAR J.Nγfor rough strip footing using the method of characteristics[J].Canadian Geotechnical Journal,2003,40(3):669-674.

[6] 尉学勇,王晓谋,怀超.斜坡地基极限承载力上限解计算与分析[J].岩土工程学报,2010,32(3):381-387.

WEI Xueyong,WANG Xiaomou,HUAI Chao.Calculation and analysis of upper limit solution of ultimate bearing capacity of sloping ground[J].Chinese Journal of Geotechnical Engineering, 2010,32(3):381-387.(In Chinese)

[7] 王晓谋,徐守国.斜坡上的地基承载力的有限元分析[J].西安公路学院学报,1993,13(3):13-17,57.

WANG Xiaomou,XU Shouguo.FEM analysis of bearing capacity of foundation on slopes[J].Journal of Xi’an Highway Transportation University,1993,13(3):13-17,57.(In Chinese)

[8] 胡卫东,曹文贵,袁青松.临坡双层粘土地基极限承载力的上限分析[J].湖南大学学报:自然科学版,2016,43(1):110-116.

HU Weidong, CAO Wengui,YUAN Qingsong.Upper bound solution for ultimate bearing capacity of the two-layer clay foundation adjacent to slope[J].Journal of Hunan University:Natural Sciences, 2016, 43(1):110-116.(In Chinese)

[9] MIZUNO T, TOKUMITSU Y, KAWAKAMI H.On the bearing capacity of a slope on cohesionless soil[J].Japanese Society of Soil Mechanics and Foundation Engineering,1960,1(2):30-37.

[10]KUSAKABE O,KIMURA T,YAMAGUCHI H.Bearing capacity of slopes under strip loads on the top surfaces[J].Japanese Society of Soil Mechanics and Foundation Engineering,1981,21(4):29-40.

[11]CASTELLI F,MOTTA E.Bearing capacity of strip footings near slopes[J].Journal of Geotechnical and Geological Engineering,2010,28(2):187-198.

[12]杨峰,阳军生,张学民,等.斜坡地基单侧滑移破坏模式及承载力上限解[J].工程力学,2010,27(6):162-168.

YANG Feng,YANG Junsheng,ZHANG Xuemin,etal.One-side slip failure mechanism and upper bound solution for bearing capacity of foundation on slope[J].Engineering Mechanics,2010,27(6):162-168.(In Chinese)

[13]赵炼恒,罗强,杨峰，等.临坡条形基础极限承载力上限计算[J].武汉理工大学学报:交通科学与工程版,2010,34(1):84-87.

ZHAO Lianheng,LUO Qiang,YANG Feng,etal.Bearing capacity of strip footing adjacent to slope with upper bound theorem[J].Journal of Wuhan University of Technology：Transportation Science & Engineering, 2010,34(1): 84-87.(In Chinese)

[14]GRAHAM J, ANDREWS M, SHEILDS D H.Stress characteristics for shallow footings in cohesionless slopes[J].Canadian Geotechnical Journal, 1988, 25(2): 238-249.

[15]胡卫东,曹文贵.基于双侧非对称破坏模式的临坡地基承载力极限平衡分析方法[J].土木工程学报,2015,48(1): 120-128.

HU Weidong, CAO Wengui.The limit equilibrium method for ultimate bearing capacity of ground foundation adjacent to slope based on bilateral asymmetry failure mode[J].China Civil Engineering Journal, 2015,48(1):120-128.(In Chinese)

[16]SOKOLOVSKII V V.Statics of soil media[M].London: Pergamon Press,1965: 1-110.

[17]TERZAGHI K, PECK R B.Soil mechanics in engineering practice[M].New York: John Wiley and Sons,1967:5-96.

[18]张学言.岩土塑性力学[M].北京:人民交通出版社,1993: 232-330.

ZHANG Xueyan.Geotechnical plastic mechanics[M].Beijing: China Communications Press,1993: 232-330.( In Chinese)

[19]王红雨,杨敏.基坑附近既有建筑物地基承载力减损的估算[J].土木工程学报,2005,38(8):95-101.

WANG Hongyu, YANG Min.An estimate for the loss of bearing capacity of the footing near excavations[J].China Civil Engineering Journal,2005,38(8):95-101.(In Chinese)

[20]胡卫东,曹文贵.基于Meyerhof理论的临坡地基极限承载力简化分析方法[J].湖南大学学报:自然科学版,2015,42(1): 81-89.

HU Weidong, CAO Wengui.A simplified analysis method for the ultimate bearing capacity of ground foundation near slope based on the theory of Meyerhof[J].Journal of Hunan University:Natural Sciences, 2015,42(1):81-89.(In Chinese)

[21]MICHALOWSKI R L.An estimate of the influence of soil weight on bearing capacity using limit analysis[J].Soils and Foundations,1997,37(4):57-64.

[22]SHIELDS D,CHANDLER N,JACQUES G.Bearing capacity of foundations in slopes[J].Journal of Geotechnical Engineering,1990,116(3):528-537.

[23]王红雨,杨敏.极限荷载作用下临近基坑c-φ土地基的破坏模式[J].岩土力学,2007,28(8):1677-1681.

WANGHongyu,YANGMin.Analysisofc-φsoils failure zone of footings near excavations under ultimate load[J].Rock and Soil Mechanics,2007,28(8):1677-1681.(In Chinese)

Simplified Analysis Method of Ultimate Bearing Capacityfor Footings Near Slope Based on Slip Line Theory

HU Weidong1, 2†，CAO Wengui1

(1.Geotechnical Engineering Institute, Hunan University, Changsha 410082, China;2.College of Civil Engineering & Architecture, Hunan Institute of Science and Technology, Yueyang 414000, China)

On the basis of the existing researches，Hill failure mechanism and its slip line solution for the ultimate bearing capacity of flat ground foundation and slope foundation were put forward without considering the foundation soil gravity.The failure mechanism of the strip footings near slope was a continuous variation mode.It should be between failure modes of the flat ground foundation and slope foundation.In the same boundary conditions，the bearing capacity of the slip line solution was a continuous function between the two critical foundation states，as the distance from the top of slope was variable.The bilateral asymmetric Hill failure mode of the strip footing near slope was thus put forward.Then，on the basis of the study，the basal pressure zone was divided into two uniform compressive areas by introducing the width ratio.The stress influence on the slope slider was simplified by using the equivalent free surface.The limit pressure on the slope slide can be then calculated by slip line solution for the slope foundation.The function of the width ratio was set by analyzing the relationship among the width ratio，the distance from the top of slope and failure mode.A new method to determine the ultimate bearing capacity of the strip footing adjacent to slope was then put forward based on the theory of slip line.Finally，the feasibility and rationality of the proposed approach were verified through the comparison with current research results.

foundation near slope; strip footings; bearing capacity；slip line; Hill failure mechanism

1674-2974(2017)07-0162-08

10.16339/j.cnki.hdxbzkb.2017.07.021

2016-03-29

国家自然科学基金资助项目(51378198), National Natural Science Foundation of China(51378198); 高等学校博士学科点专项科研基金资助项目(20130161110017), Research Fund for the Doctoral Program of Higher Education of China(20130161110017)

胡卫东(1976—)，男，湖南岳阳人，湖南大学博士研究生，湖南理工学院副教授†通讯联系人，E-mail: huweidong506@163.com

TU44

A