空间复杂多支管柱节点受力性能研究*

胡浩，李正良，刘红军，钱秋羽，陈远川

(1.重庆大学 土木工程学院，重庆 400045; 2.重庆文理学院 建筑工程学院，重庆 400045；3.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

空间复杂多支管柱节点受力性能研究*

胡浩1,2,3†，李正良1,3，刘红军1,3，钱秋羽1,3，陈远川2

(1.重庆大学 土木工程学院，重庆 400045; 2.重庆文理学院 建筑工程学院，重庆 400045；3.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

对钢管塔架中空间多支管柱节点进行了足尺模型试验，试验装置采用自平衡框架，共制作了2个试验试件.在试验结果的基础上，建立了非线性有限元模型，所得结果与试验结果相比，二者吻合良好，表明有限元模型的合理性，并进行了有限元参数分析.结果表明,试验模型节点主要发生主管压曲的变形破坏，且未出现支管和焊缝的破坏；加载至设计荷载值时，节点所有测点基本处于线弹性状态，表明节点设计较安全.主管径厚比对节点极限承载力影响显著，主管直径较大时，承载力随主管壁厚增大而上升较快；主管直径较小时，承载力随主管壁厚增大而上升较慢.受压支管直径及壁厚较小时，易发生自身弯曲失稳破坏.

多支管节点；极限承载力；足尺试验；有限元分析

钢管塔节点是输电塔及塔架建筑中的重要部件，目前国内外关于钢管塔节点承载力的研究比较充分，1981年，Yura[1]总结了80年代以前关于钢管节点的研究成果，提出了改进的节点强度公式，并对收集的实验数据进行筛选，建立了一个由137个试验结果组成的可靠数据库.1996年，Makino等[2]在以往钢管节点试验数据的基础上建立了一个由1 544个实测结果和786个有限元分析结果组成的数据库，节点形式包括T,Y,X,K,TT,XX,TX,KK型.陈继祖等[3]对各国规范的极限承载力公式进行了深入分析，并根据我国钢结构设计规范设计原则和国内钢结构行情，提出了承载力设计公式.Saeko[4],Okumura[5]在少量试验基础上，对K,TY,X型钢管插板节点承载力进行了研究，并提出了一个非常保守的计算公式.Thornton[6]改进了Whitmore的有效宽度法，提出了用等效柱条法研究节点板的承载力.Yam等[7]又改进了Thornton的方法，将节点板的应力扩散角由原来的30度改为45度.Kim[8]对插板连接节点进行了缩尺试验和有限元分析，提出了节点弯矩和支管轴力的承载力计算公式.陈以一等[9]总结了国内外关于钢管结构和相贯节点的类型及其承载力性能试验、强度计算研究进展.刘红军等[10]通过试验对钢管环型加肋节点的极限承载力进行了研究，并借助有限元对此类节点进行参数分析，利用虚功原理提出了适用于估算此类节点极限承载力的极限分析模型和工程设计建议计算公式.郭小农等[11-12]通过试验及有限元手段研究了板式节点的受弯性能，并给出该节点面外初始弯曲刚度的杆件间交互影响程度的理论计算公式.国内外研究者也提出了相关的指导设计规范[13-15].

上述钢管节点杆件较少，构造简单，然而，国内外关于空间复杂多支管节点的研究较少，对于该类节点必须通过试验得到其极限承载力及破坏模式[16-17].

青海佑宁750 kV变电站钢管格构式塔架项目，提出了一种复杂的柱节点，钢管格构柱在等宽度的窄面节点采用相贯焊、变宽度的宽面节点仍然采用节点板螺栓连接.通过对其进行足尺试验及有限元分析，以研究此节点的受力特性，最后通过试件参数分析，为后续回归分析确定该类节点的承载力计算公式奠定基础.

1 试验设计

1.1 试件设计

制作了2个试验节点相同的试验试件，以便降低误差.节点构造及受力形式如图1所示，图中虚线表示杆⑦，其与支管③、⑤在同一平面内，且杆⑦轴线与支管③、⑤轴线夹角均为45o.受拉杆⑦为角钢与节点板JDB2(连接节点板JDB1和支管③)直接通过螺栓连接.非螺栓连接处均采用焊接，角焊缝尺寸按相关规范确定.各杆件截面尺寸、连接方式、承载力设计值Ni及材料性能试验结果见表1和表2.

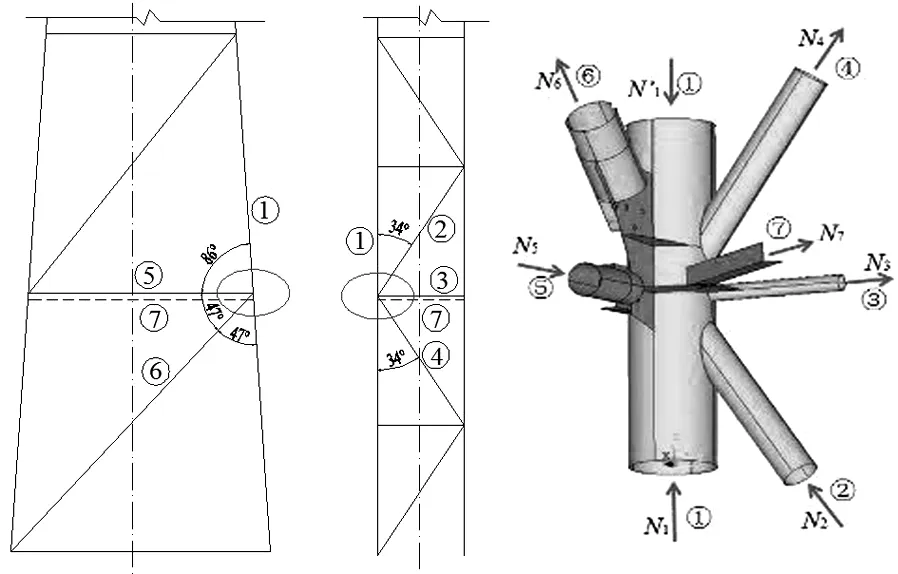
(a)正立面 (b)侧视图 (c)节点受力图1 节点形式Fig.1 Type of joint

杆件编号连接方式Ni/kN相连处插板和节点板规格及编号①-13331732-②相贯焊接235-③相贯焊接-20-④相贯焊接-193-⑤螺栓连接39[12H/2M20-12H/6CB1,JDB1⑥螺栓连接-44T12H/6/4M20-12H/6CB2,JDB1⑦螺栓连接-62M16-8HJDB2

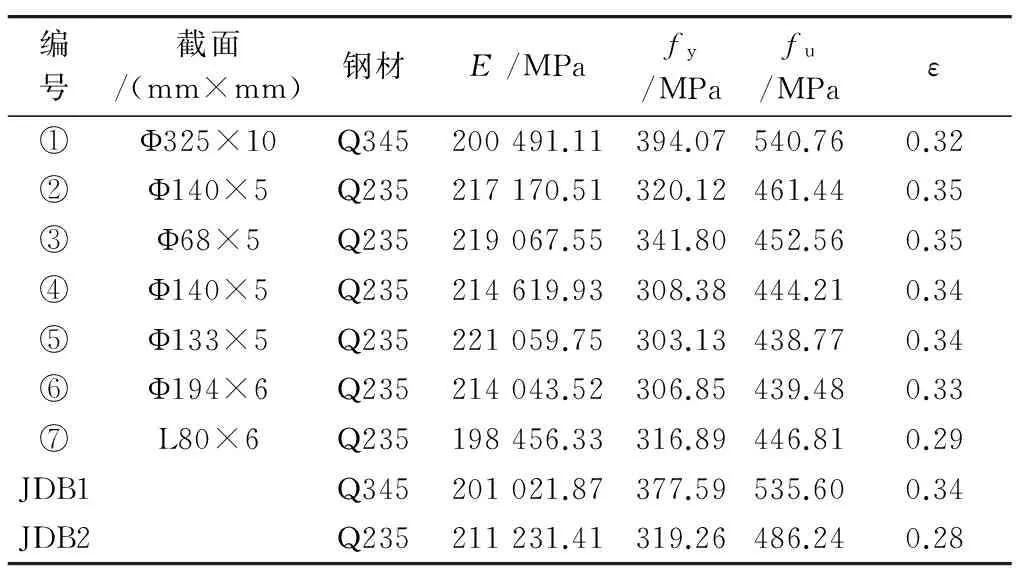
表2 各杆件的钢材力学性能

注：E为钢材弹性模量;fy为钢材屈服强度;fu为钢材抗拉强度;ε为材料延伸率.

1.2 试件加载及测点布置

试验中专门设计了一套具有足够刚度的加载装置，即自平衡框架见图2.平衡框架由4根横梁通过高强螺栓首尾连接，对该面内管件加载的千斤顶由拉耳通过高强螺栓连接在平衡框上，用于加载平面外斜支管的千斤顶通过螺栓连接在单根柱子上或者连接在平面外的横梁上，柱子由地脚螺栓固定于实验室，同时与平衡框通过拉杆连接，该试验在重庆大学大型结构实验室完成.

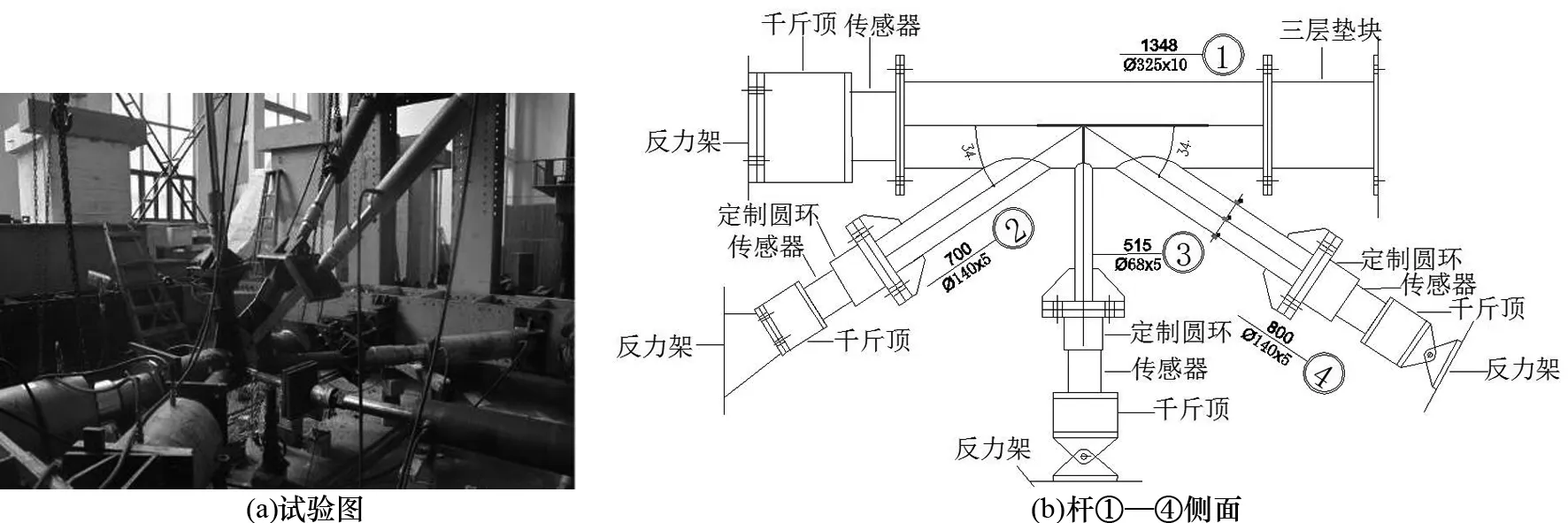
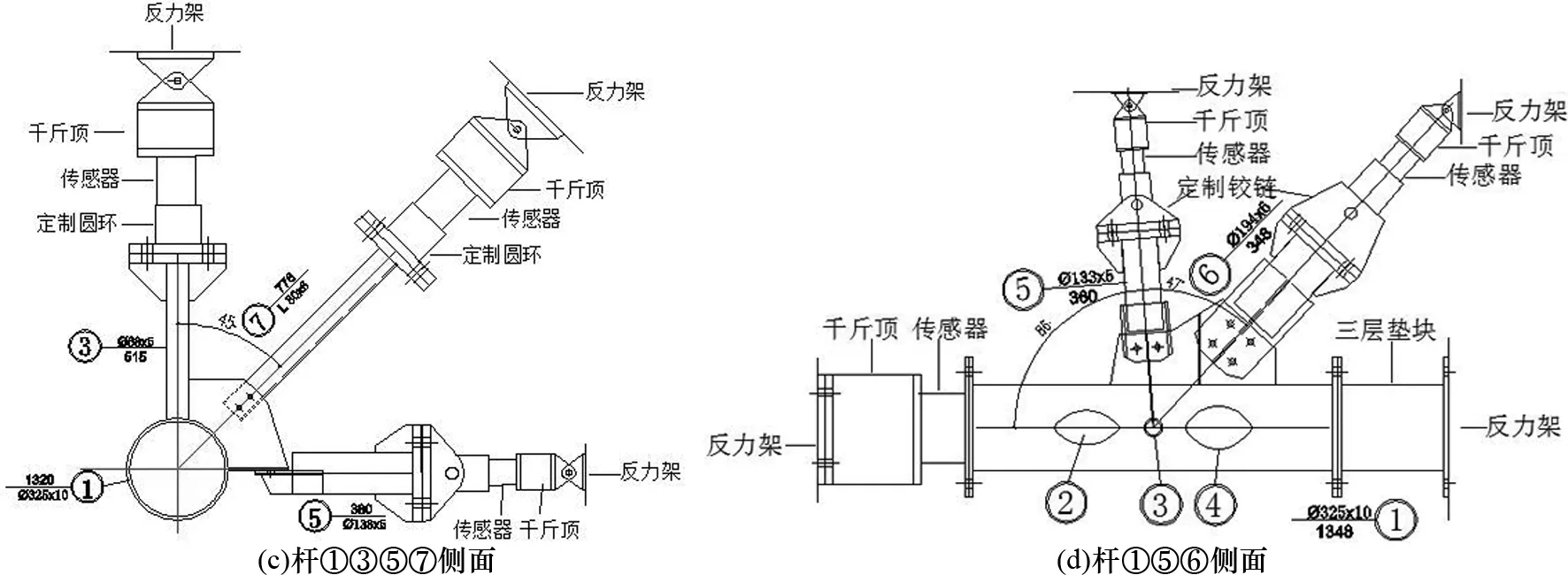
图2 试验装置图Fig.2 The test setup

节点各杆件均承受轴力，需对千斤顶实施同步等比例静力加载，由于个别杆件为辅材且受力较小，对该类杆件采取被动加载的方式.支管⑤和杆⑦都由千斤顶提供支座反力，不进行主动加载，但通过传感器读取其实际轴向受力值，其他杆件由千斤顶直接加载.

图3给出了各管端实测荷载与目标加载的关系曲线，实际加载级即实际加载与设计荷载的比值，目标加载级即目标加载与设计荷载的比值.由图3可知，主动加载的各管实测加载值与目标加载值比较吻合，两试件中被动加载的支管实测加载值与目标加载值具有一定差距，但加载过程中实测值变化趋势比较接近.

试件安装后，采取单调静力加载，先用高精度激光投线仪进行几何对中，完毕后，采用小幅轴压力进行预加载，利用每根杆件同一截面的电阻应变片进行物理对中，使每一片电阻应变片的读数和所有电阻应变片读数的平均值相差在5%以内，并使各部分接触良好.节点中主管预加载大小是设计荷载的20%，支管预加载大小是设计荷载的5%；预加载卸载后开始正式加载，按照每级施加设计荷载的10%，直至加载到设计荷载，再按照每级施加设计荷载的5%，直至加载到设计荷载的200%，最后按照每级施加设计荷载的2%，每级加载稳定1 min后记录相应荷载的应变.直至加载时出现管件所对应的应变仪数据波动较大，无法稳定自动卸荷的情况时停止加载.

试件上布置单向应变片、三向应变花及三向位移计测量节点区应变及位移，应变片及位移计布置见图4.图中单个矩形块代表单向应变片，3个矩形块代表三向应变花，符号D1,D2和D3分别表示节点竖向、水平向和轴向位移计，3个位移计在同一平面内.

(a)节点4-1试件 (b) 节点4-2试件图3 节点实测荷载与杆端加载的比较Fig.3 Comparison between experimental value and cell value for loading

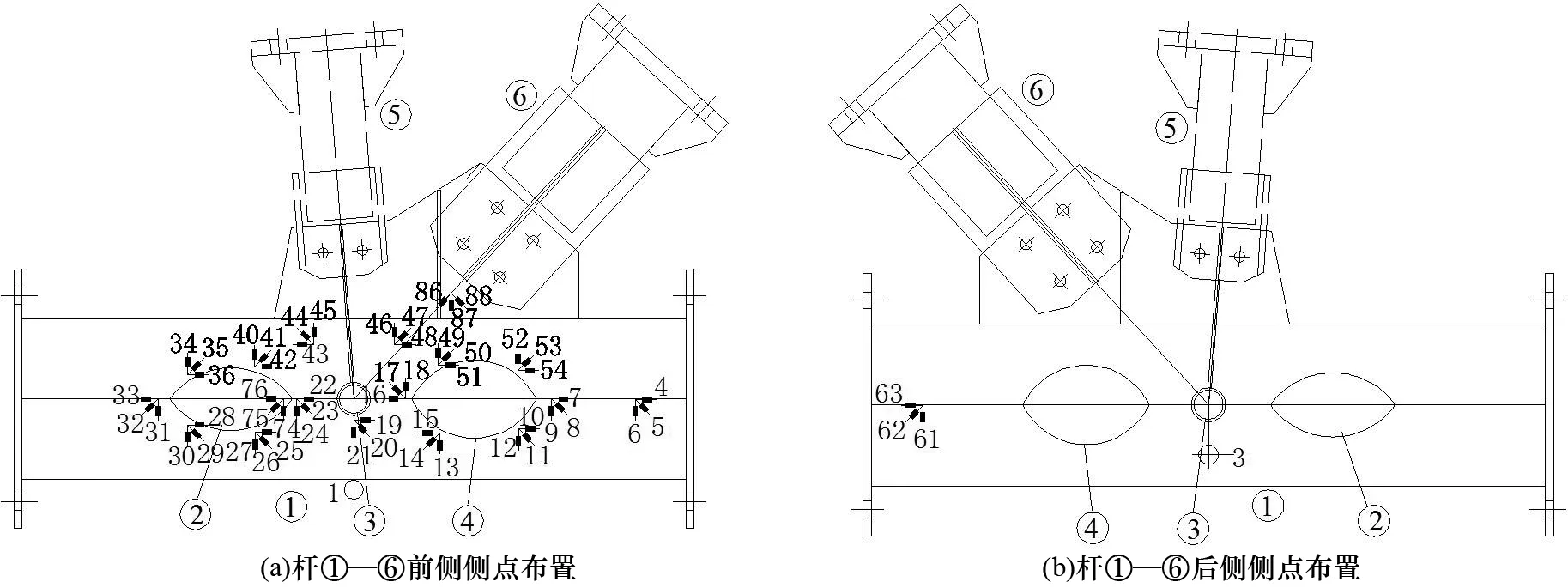
图4 节点位移计和应变片布置Fig.4 Arrangement of displacement and strain meters

2 试验现象及结果

通过分析测点数据可知，对于柱节点两试件，编号分别为试件4-1和试件4-2，荷载最终分别施加至设计值的2.12和2.16倍时，出现千斤顶无法继续加载，传感器数值波动较大，部分管件出现卸载的情况，即试件4-1中管件①，②，⑥，杆⑦及试件4-2中支管②，⑥，杆⑦，加载结束时，支管②端部主管壁压曲较严重，主管发生了较大塑性变形，且凹曲处主管上下侧均鼓出，鼓出变形大小接近，见图5，节点其他部位未发现明显破坏现象.

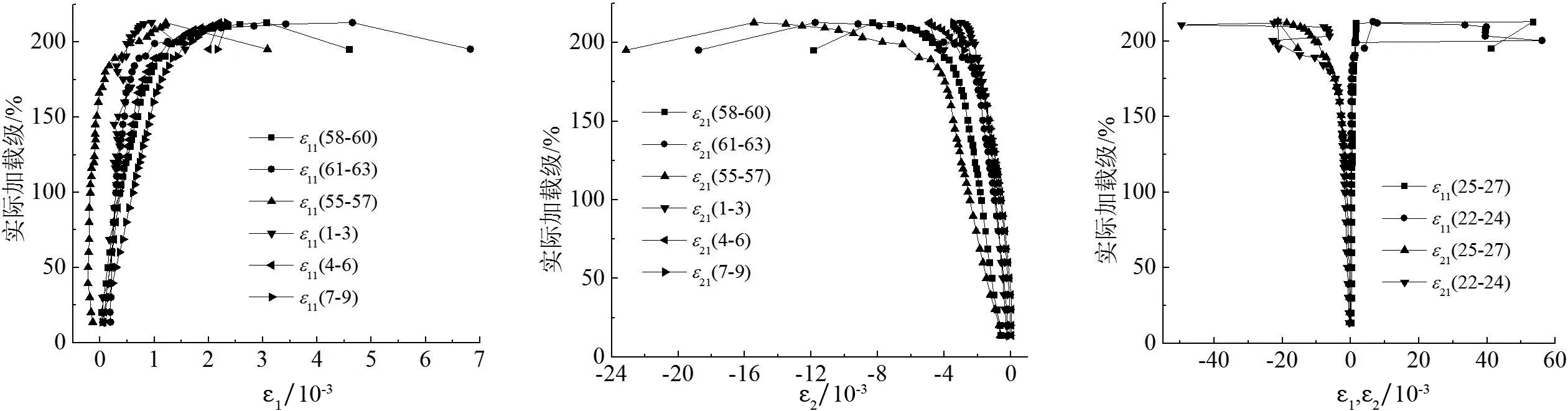
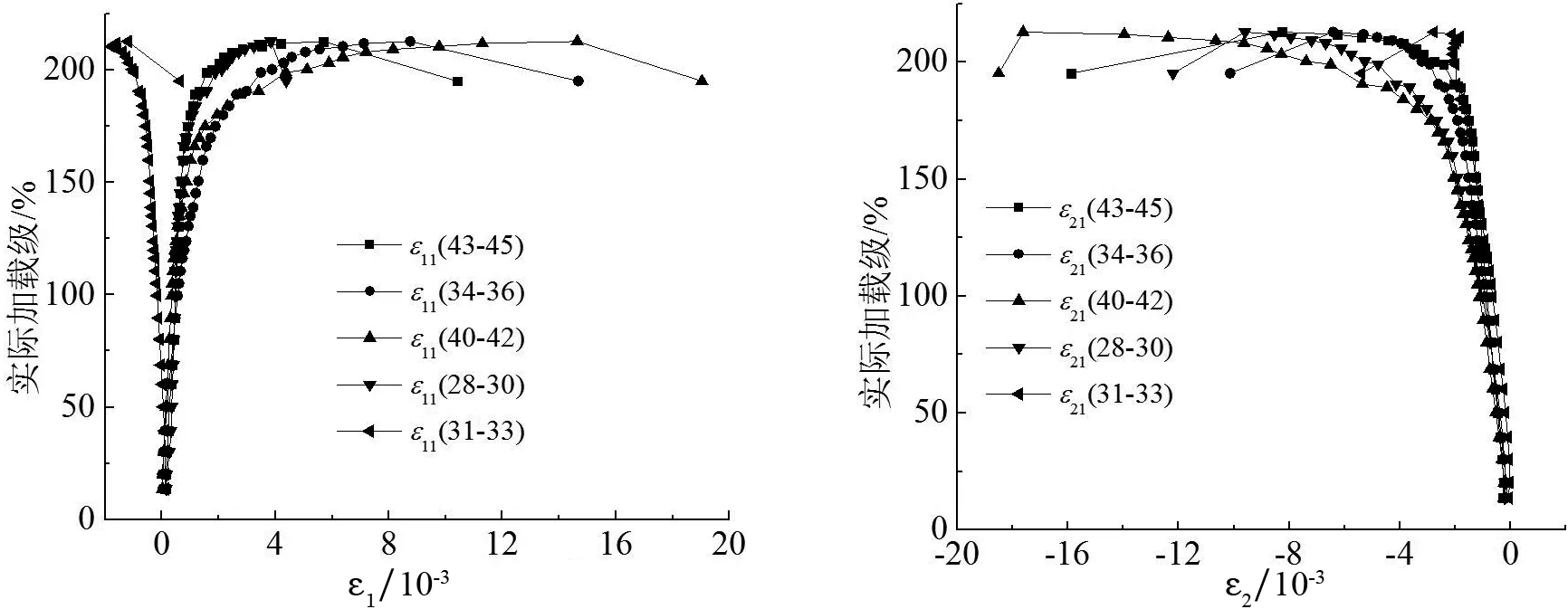
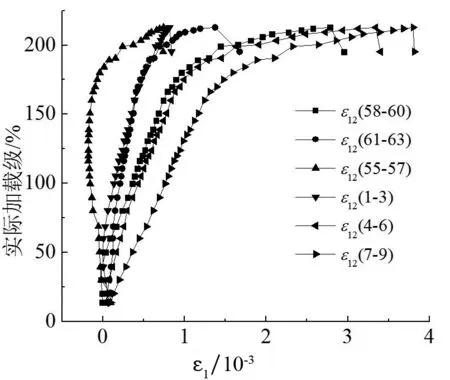
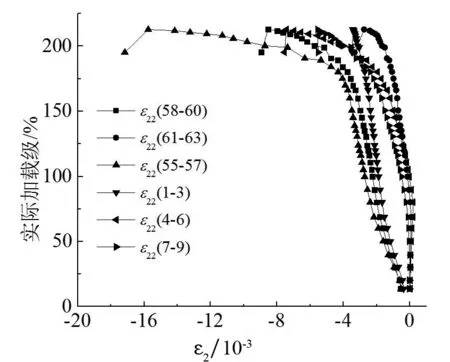
由于节点杆件较多，仅以某个杆件的实际加载值作为节点承载力欠妥，考虑到试验中，主管在支管②轴力作用下压屈破坏，故以支管②实际加载值与自身设计承载力的比值来表征节点承载力.因此，以该比值为纵坐标，测点主应变为横坐标，给出两试件部分测点的主应变变化曲线，分别见图6和图7.符号εij(x-y)表示试件j中应变花测点编号x至y的第i个主应变值.

图6(a)和(b)，图7(a)和(b)分别表示两试件主管两端测点的主应变曲线.由图可见，由于主管非加载端所受合力较大，测点极限应变也较大.加之空间各支管对主管的共同作用，使得主管截面受力不均匀，同一圆周上的测点1-3，4-6，58-60，61-63应变大小也不一样.试件4-1测点55-57，58-60，61-63应变较大，测点1-3，4-6，7-9应变较小，试件4-2测点4-6，7-9，55-57，58-60应变较大，测点1-3，61-63应变较小，但二者整体变化趋势比较相似.

(a)柱节点试件4-1 (b)柱节点试件4-2图5 节点破坏模式Fig.5 Failure mode of column joint

(a)第1主应变 (b)第2主应变 (c)第1和第2主应变

(d)第1主应变 (e)第2主应变图6 试件4-1荷载级-应变曲线Fig.6 Load-strain curves of the specimen 4-1

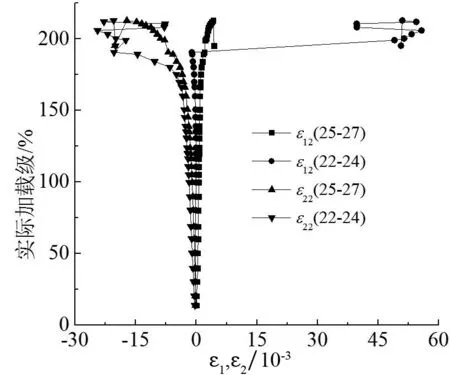
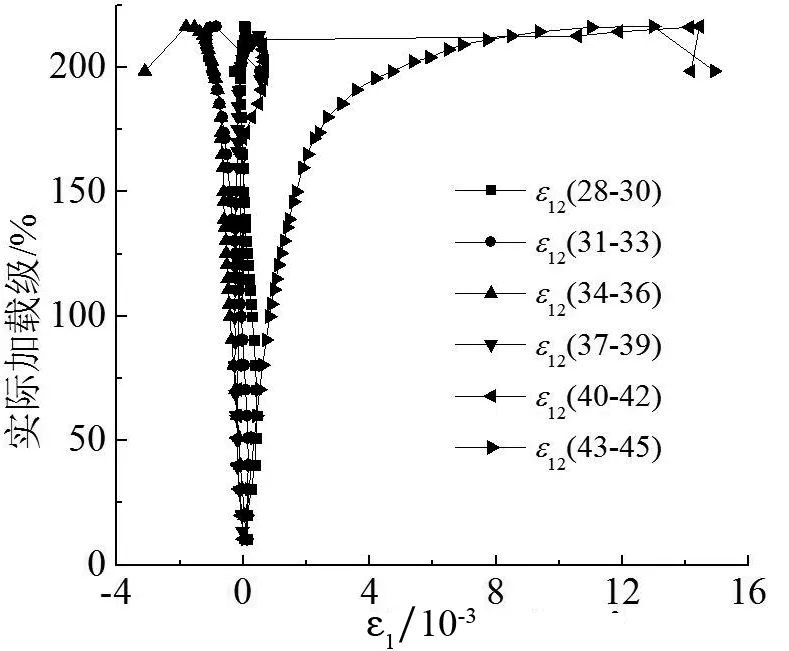
图6(c)(d)(e)，图7(c)(d)(e)分别给出两试件支管②端部附近主管壁上测点主应变曲线.由图可知，测点22-24和25-27达到屈服之前，应变增长较慢，但拉压主应力增长较均匀达到屈服之后，应变值出现突变式增长，主管迅速出现凹曲破坏.测点28-30和34-36拉压主应变都较大，但进入屈服之后，前者主压应变增长较快，后者主拉应变增长较快.测点40-42拉压主应变最大，试件4-1中，两主应变变化趋势及数值很接近，屈服之后，增长较快；试件4-2中，屈服之后，两主压应变增长较快，至加载后期，均出现波动，同时测点43-45处塑性变形发展也很充分.测点31-33拉压主应变相对较小，此处主管变形较小，综上可知，支管②端部相贯线外侧冠点附近主管变形较小，内侧冠点附近主管变形较大，沿着逆时针观察发现，主管变形逐渐加大，且上侧相贯线测点由受拉压逐渐向受拉为主转变.可见两试件应变分布较为接近，表明误差控制较好.

(a)第1主应变

(b)第2主应变

(c)第1和第2主应变

(d)第1主应变

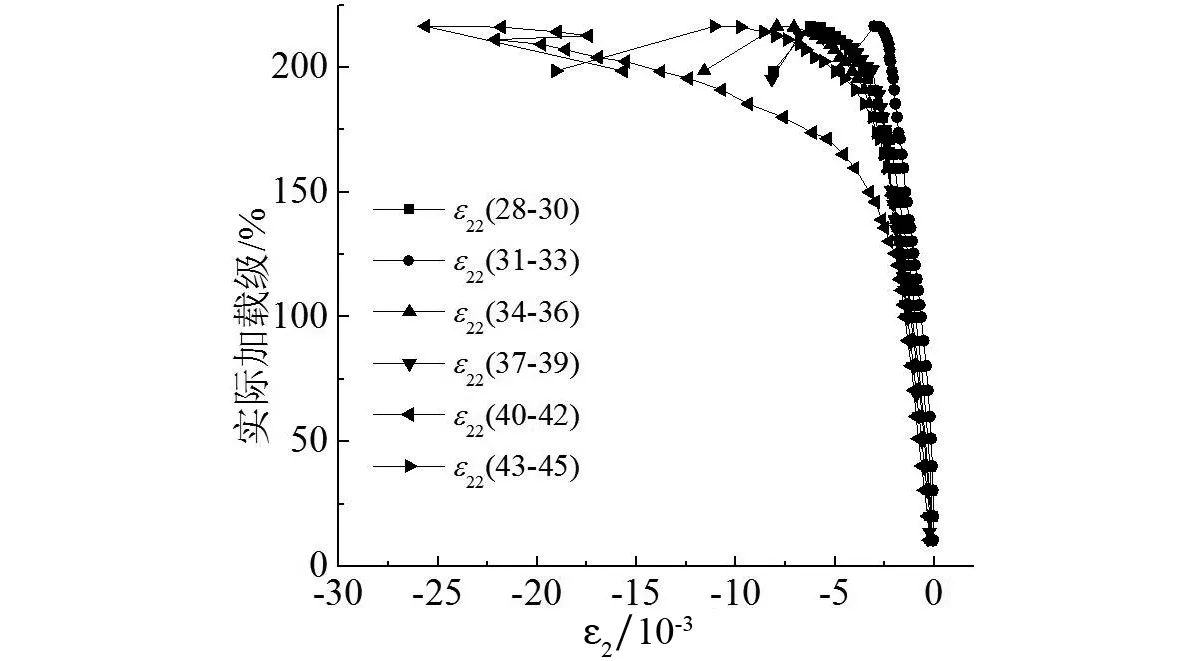
(e)第2主应变图7 试件4-2荷载级-应变曲线Fig.7 Load-Strain curves of the specimen 4-2

3 有限元分析

3.1 节点破坏模式

在试验的基础上，采用软件ANSYS建模进行有限元分析，节点模型采用SHELL181壳单元模拟，不考虑焊缝的影响，构件与节点板螺栓孔连接处采用MPC184单元模拟，忽略螺栓孔处构件与节点板的相对滑移，模型共划分为33 812个单元.考虑节点模型的几何非线性、材料非线性，钢材本构关系采用多线性模型及等向强化理论，节点单元划分如图8所示，弹性模量、屈服强度及极限强度取材性试验数据.材料弹塑性的发展和单元刚度由Mises屈服准则及关联流动法则确定，应用弧长法计算.主管一端按固定支座考虑，另一端为仅有沿主管轴线方向位移的固定支座.主动加载的支管端部边界为滑动铰支座，仅允许沿杆轴线方向有位移，约束径向位移；被动加载的支管处千斤顶会发生不同程度的拉伸或压缩，故根据试验结果及分析，约束径向位移，允许其轴线方向产生适量位移.未考虑各杆件端部端板及加劲板的影响，荷载及约束直接施加在杆件端部节点上.

(a)本构关系 (b)模型单元图图8 本构关系及模型单元图Fig.8 Material behavior and elements of the joint

有限元分析所得节点的破坏模式见图9，与图5相比可知,有限元模拟所得节点的破坏形态与试验结果基本相同,即支管②端部主管壁发生了压曲塑性变形破坏,且压曲处主管上下侧均鼓出.

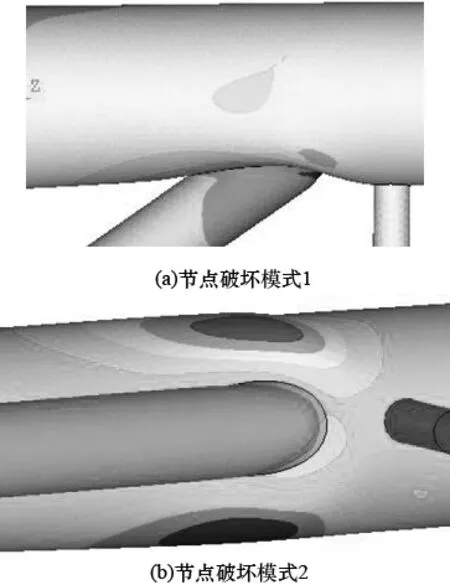
图9 节点破坏模式的有限元分析Fig.9 Failure modes of FEA

3.2 节点承载力

节点3个方向加载级-位移曲线见图10，所测位移方向见图4位移计布置图.由位移曲线可知，在线性范围内，有限元分析结果与试验结果基本一致；荷载施加至最大时，水平位移较小，竖向和轴向位移较大.

根据钢管节点承载力判断准则[18]，有限元分析所得试件极限承载力同试验结果对比见表3，表中Ret表示试验承载力与设计荷载的比值，Ree表示有限元计算值与设计荷载的比值.由表3可见，有限元值与试验值较接近，误差在允许范围内.综上表明有限元模型的合理性和可靠性

表3 节点承载力有限元分析与试验值比较

4 有限元参数分析

对节点进行有限元参数分析时，主要考察节点几何参数变化对其极限承载力的影响.有限元模型材料、约束及加载比例同原模型，考虑到杆件较多，影响节点受力特性的几何因素较多，结合试验中节点的破坏模式，确定以下参数为研究对象：主管自身径厚比γ=D1/(2T1)，支主管直径比βi=Di/D1，支主管壁厚比τi=Ti/T1(i表示第i根支管).节点极限承载力用Pu(kN)表示，考虑到支管④与支管②设计荷载较接近，截面尺寸相同，故将两支管取相同变化尺寸.为便于比较，统一取支管②极限轴力表征.几何参数取值如表4所示。

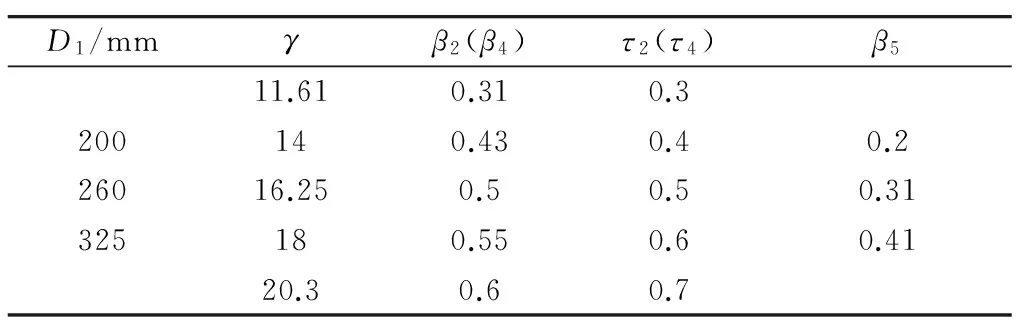
表4 节点几何参数

(a)竖向位移 (b)水平位移 (c)轴向位移图10 节点位移曲线的有限元分析与试验结果对比Fig.10 Comparison of displacement of column joint between FEA and test

根据有限元计算结果，节点主要发生以下几种破坏模式，如图11所示.支管②端部局部屈曲破坏BLB2；支管②整体弯曲失稳破坏BB2；支管②端部主管受压凹曲塑性破坏CLD1；支管④端部主管受拉凸出塑性破坏CLD2；支管⑤整体弯曲失稳破坏BB5.

(a)支管②端部局部屈曲破坏BLB2 (b)支管②整体弯曲失稳破坏BB2 (c)支管②端部主管受压凹曲塑性破坏CLD1

(d)支管④端部主管受拉凸出塑性破坏CLD2 (e) 支管⑤整体弯曲失稳破坏BB5图11 节点破坏形态图Fig.11 The failure modes of the column joints

图12和图13分别为支管②直径及壁厚对节点极限承载力的影响曲线.图12中，支管②直径及壁厚较小时，随着β2增大，Pu上升较多；当β2较大时，随着β2增大，Pu上升不太明显，且有下降趋势.主要因为随着支管β2，τ2的增大，节点破坏模式从支管②整体弯曲失稳破坏BB2向主管的破坏CLD1,CLD2转变，若保持τ2不变，β2继续增大，则支管②自身径厚比变大，节点发生局部屈曲破坏BLB2，承载力略降.同理，图13中，支管②直径及壁厚较小时，随着τ2增大，Pu上升较多；当τ2较大时，随着τ2增大，Pu上升很缓慢.图12(c)及图13(c)(d)中，节点主要发生主管塑性变形破坏并伴有支管②的BLB2及BB2破坏模式，故随着β2和τ2的增大，其与主管相贯面积变大，节点极限承载力Pu增大.

图12 β2的影响Fig.12 Influence of β2 on the ultimate strength

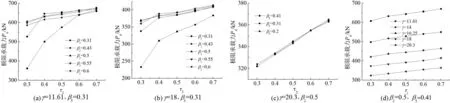
图13 τ2的影响Fig.13 Influence of τ2 on the ultimate strength

图14为支管⑤直径对节点极限承载力的影响曲线.由于支管⑤的设计荷载很小，故当支管⑤直径仅为主管直径的0.2时，节点承载力也不会降低，始终取决于主管管壁的强度.所以改变支管⑤直径对节点极限承载力无影响.

图15为主管截面尺寸对节点极限承载力的影响曲线.综合上文分析结果，并结合图15可知，当节点主要发生主管塑性变形破坏时，随着γ减小，极限承载力几乎呈直线上升，说明主管管壁厚度越大，节点承载力越高；当主管直径较大时，承载力随主管壁厚增大而上升得较快；当主管直径较小时，承载力上升的趋势较缓慢.当其他参数不变,相同主管壁厚情况下，主管直径越大，承载力越高，主管厚度和直径对承载力大小均有较大影响.

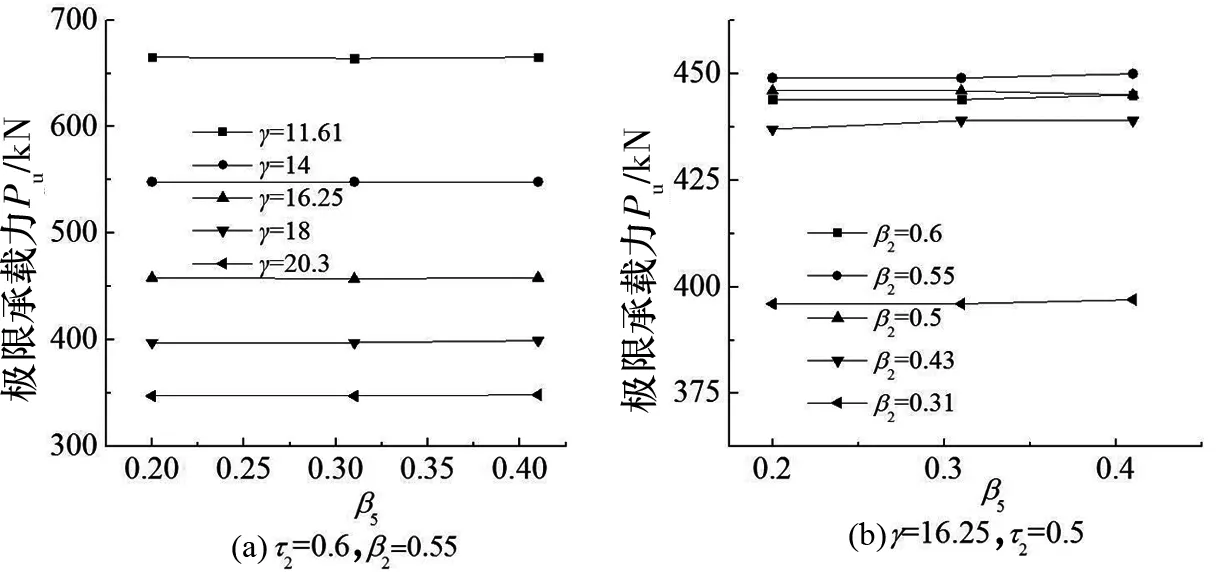
图14 β5的影响Fig.14 Influence of β5 on the ultimate strength

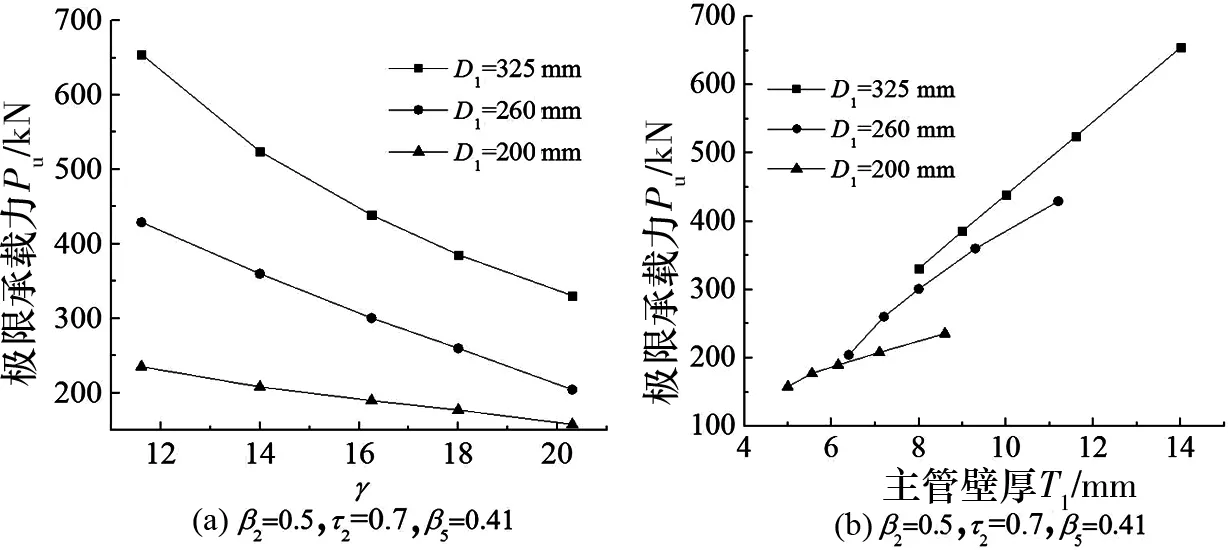
图15 主管对节点极限承载力的影响Fig.15 The influence of chord on the ultimate strength

通过有限元参数分析，可知：

1)当β2≤0.31，τ2≤0.4时，节点主要发生支管②整体弯曲失稳破坏BB2.主要因为支管②轴力较大，其直径很小，管壁较薄，在主管受压达到屈服变形前，支管已承受不了轴力而失稳破坏.

2)当14≤γ≤20.3，β2≥0.43，τ2≥0.4时，塑性区域首先出现在主管与支管②相贯处附近，主管最终受压凹曲，节点发生塑性破坏，此时γ越大，主管管壁凹陷越明显.主要因为支管②轴向刚度较大，而主管环向刚度相对较小，支管轴力直接传递到主管管壁上而产生管壁塑性破坏.支管②随着主管变形发生相应变形，若支管②直径较大、管壁较薄(β2≥0.55，τ2≤0.5)，则相贯处支管②端部易发生局部失稳变形，支管轴力无法传递到主管上，节点承载力下降.

3)当D1≤200 mm，β2和β4≥0.55，τ2和τ4≥0.4时，在支管④轴力作用下，主管受拉向外凸出，节点发生CLD2破坏.当D1≤200 mm，β5<0.2时，支管⑤由于太细长会发生弯曲变形，此时承载力很小，节点发生支管⑤整体弯曲失稳破坏BB5.

5 结 论

1)节点两试件极限承载力分别为其设计荷载值的2.12倍和2.16倍，可见两试件试验所得结果很相近，表明试验误差控制较好，离散性较小，且节点具有较大的安全富余.

2)两试件主要发生支管②端部主管凹曲变形破坏，凹曲处上下侧主管管壁鼓出，且鼓出变形较接近，节点其他部位未出现明显变形，且均未出现支管和焊缝的破坏.

3) 通过对试验节点进行非线性有限元分析，并把所得结果与试验结果作对比，二者吻合较好，表明有限元模型的合理性.

4) 大量的有限元参数分析表明，主管径厚比γ对节点极限承载力影响显著.主管直径较大时，承载力随主管壁厚增大而上升较快；主管直径较小时，承载力上升较慢.受压支管直径及壁厚较小时，易发生自身受压弯曲失稳破坏.

[1] YURA J A.Ultimate capacity of circular tubular joints[J].ASCE，1981，107(10):1965-1984.

[2] MAKINO Y，KUROBANE Y，OCHI K，etal.Datebase of test and numerical analysis results for unstiffened tubular joints[R].Villepinte，France：International Institute of Welding，1996:601-608.

[3] 陈继祖,陆化普.焊接管节点设计承载力公式研究[J].大连工学院学报，1996,25(2):47-52.

CHEN Jizhu，LU Huapu.The study of the bearing capacity formula for the design of welded tubular joints[J].Journal of Dalian Institute of Technology，1996，25(2):47-52.(In Chinese)

[4] SAEKO S.Experimental study on strength of tubular steel structures [J].Japanese Society of Steel Construction，1974，10(102):37-68.

[5] OKUMURA T.Research on steel structures-memorial for Prof.Okumura Toshie's age of threescore[M].Tokyo：Gihodo Press，1977:520-525.

[6] THORNTON W A.Bracing connections for heavy construction[J].Engineering Journal AISC，1984，21(3):139-148.

[7] YAM M C H，SHENG N，IU V P，etal.Analytical study of the compressive behaviour and strength of steel gusset plate connections[C]//Proceedings of the CSCE Annual Conference.Halifax：Nova Scotia，1998：97-106.

[8] KIM W B.Ultimate strength of tube-gusset plate connections considering eccentricity[J].Engineering Structures，Elsevier，2001，23(11)：1418-1426.

[9] 陈以一，陈扬骥.钢管结构相贯节点的研究现状[J].建筑结构，2002，32(7)：52-55.

CHEN Yiyi，CHEN Yangji.Research status of tubular joints of steel tubular structure[J].Building Structure，2002，32(7)：52-55.(In Chinese)

[10]刘红军，李正良，李茂华.钢管输电塔环型加肋节点极限承载力研究[J].工程力学，2010，27(10)：65-73.

LIU Hongjun，LI Zhengliang，LI Maohua.Study of ultimate strength of steel tubular joint with annular ribbed plate of transmission towers[J].Engineering Mechanics，2010，27(10)：65-73.(In Chinese)

[11]郭小农，邱丽秋，罗永峰，等.铝合金板式节点受弯承载力试验研究[J].湖南大学学报:自然科学版，2014，41(4):47-53.

GUO Xiaonong，Qiu Liqiu，LUO Yongfeng，etal.Experimental research on the bending capacity of aluminum alloy gusset joint [J].Journal of Hunan University:Natural Sciences，2014，41(4):47-53.(In Chinese)

[12]郭小农，熊哲，罗永峰，等.铝合金板式节点面外初始弯曲刚度的杆件间交互影响[J].湖南大学学报:自然科学版，2015，42(3)：36-42.

GUO Xiaonong，XIONG Zhe，LUO Yngfeng，etal. The out-of-plane initial bending stiffness interaction of members on the aluminum alloy gusset joint[J].Journal of Hunan University:Natural Sciences，2015，42(3)：36-42.(In Chinese)

[13]GB 50017-2003 钢结构设计规范[S].北京:中国计划出版社,2003.

GB 50017-2003 Code for design of steel structures [S].Beijing：China Planning Press，2003.(In Chinese)

[14]DL/T5254-2010 架空输电线路钢管塔设计技术规范[S].北京:中国电力出版社,2010.

DL/T5254-2010 Technical regulation of design for steel tubular tower structures of overhead transmission line[S].Beijing：China Electric Power Press，2010.(In Chinese)

[15]CEN.Eurocode 3：Design of steel structures，Part 1-8:Design of joints [S].Brussels：EN1993-1-8，European Committee for Standardization，2005.

[16]赵宪忠，徐祥斌，闫伸，等.空间复杂钢管节点试验研究[J].工程力学，2010，27(S2)：207-211.

ZHAO Xianzhong，XU Xiangbin，YAN Shen，etal.Experimental study of complex multiplanar tubular joints [J].Engineering Mechanics，2010，27(S2):207-211.(In Chinese)

[17]邵铁峰，王伟，陈以一.网壳结构复杂多支管连接的试验研究[J].工程力学，2012，29 (S2)：144-148.

SHAO Tiefeng，WANG Wei，CHEN Yiyi.Experimental investigation on complex multiplanar joints of lattice shell structures [J].Engineering Mechanics，2012，29(S2)：144-148.(In Chinese)

[18]LU L H，DEWINKEL G D，YU Y，etal. Deformation limit for the ultimate strength of hollow section joints[C]// Proceedings of Sixth International Symposium on Tubular Structures.Rotterdam：Balkema，1994：341-347.

Research on Mechanical Properties of Spatial ComplexMulti-planar Column Joints

HU Hao1,2,3†,LI Zhengliang1,3，LIU Hongjun1,3，QIAN Qiuyu1,3，CHEN Yuanchuan2

(1.School of Civil Engineering，Chongqing University，Chongqing 400045，China; 2.School of Architectural Engineering,Chongqing University of Arts and Sciences,Chongqing 400045,China; 3.Key Laboratory of New Technology forConstruction of Cities in Mountain Area(Chongqing University),Ministry of Education，Chongqing 400045，China)

The structural behavior and load-carrying capacity of multi-planar column joints in a tubular tower were investigated under static loading in the test instrument of self-balancing frame with two full-scale test specimens.Based on this，the nonlinear finite element models were established.The analysis results were compared with the experimental results，which showed good agreement.The parametric analyses were also performed by reasonable and credible finite element models.The investigation indicates that the concave deformation occurs in their main pipes without the failure of branches and welds.All the measuring points of the joints are basically kept in linear elastic condition under design loads，showing that the design for the joint is very safe.Moreover，the ratio of chord radius to thickness has significant influence on the ultimate strength.The load-carrying capacity of the joint is improved with the growth of wall thickness when the diameter of chord is large.However，it increases slowly with the increase of wall thickness when the diameter is small.The brace with small diameter and wall thickness is easily yielded and shows flexural buckling.

multi-planar joint; bearing capacity; full-scale test; finite element analysis

1674-2974(2017)07-0049-10

10.16339/j.cnki.hdxbzkb.2017.07.007

2016-06-14

国家自然科学基金资助项目(51278511，51508054)，National Natural Science Foundation of China (51278511，51508054); 重庆市科委基础与前沿研究计划项目 (CSTC2014JCYJA30019)，Chongqing Science and Technolog Commission,Foundation and Frontier Research Project(CSTC2014JCYJA30019)

胡浩(1986—)，男，安徽淮南人，重庆大学博士研究生†通讯联系人，E-mail：hhxkfy@126.com

TU392.3; TU317.1

A