两单元冗余系统的可靠性预计

汪 建，丁邦宙

(1.中国电子科技集团公司第三十八研究所，合肥 230088; 2.孔径阵列与空间探测安徽省重点实验室，合肥 230088))

两单元冗余系统的可靠性预计

汪 建1，2，丁邦宙1

(1.中国电子科技集团公司第三十八研究所，合肥 230088; 2.孔径阵列与空间探测安徽省重点实验室，合肥 230088))

比较了采用等效失效率和概率法计算两单元组成的冗余系统(包括热备和冷备)可靠度预计结果，两种方法得到的可靠度预计结果有明显差异，用等效失效率按指数分布计算得到的冗余系统可靠度偏低，指出冗余系统的可靠度不宜用等效失效率按指数分布模型进行计算。本文为大型系统的可靠性预计方法提供了一些参考。

冗余系统；失效率；指数分布；可靠性预计

0 引 言

可靠性预计是根据实际设计，对系统所能达到的可靠度进行预估。通过可靠性预计可以发现影响系统可靠性的主要因素，找出薄弱环节，采取改进措施，提高系统可靠性；为 FMEA/CA、FTA等设计分析工作提供依据；为制定研制计划、验证试验方案以及维修、后勤保障方案提供依据[1-3]。因此，可靠性预计是整个产品研制过程中必不可缺的工程活动。

目前，最常用的可靠性预计方法主要有: 元器件计数法[4,5]和应力分析法[6]等。通过可靠性预计，可以发现可靠性偏低的设备。实际应用中通常采用冗余备份设计来提高其可靠度，冗余备份系统主要有热备[7,8]和冷备[9]。热备系统是指由n个单元组成的系统，其中至少r个正常工作时，系统就能正常工作，也称为r out of n (G)系统或表决系统。冷备系统是指工作单元失效时，由检测装置探知，启动转换开关，切换备份单元投入工作的系统。

可靠性预计也不单可以用于寻找设备间的薄弱环节，还要求系统预计满足总体单体提出的可靠性指标要求。如果预计偏向保守或者出现计算误差而不能满足指标要求,则势必需要增加薄弱设备的冗余设计,这将造成不必要的浪费，有的时候增加了额外的冗余备份反而还超出了总体下发的重量、体积等指标，得不偿失;反之，如果预计偏向激进,误认为可靠性设计已经达到或超越了系统总的指标要求,从而放弃对薄弱设备的再设计或者冗余备份,那将使整个系统陷入非常危险的境地[10]。

针对大型系统进行可靠性预计时，无论是元器件计数法还是应力分析法，都是基于电子器件的寿命均服从负指数分布的情况下进行分析的。然而，对于备份后的可靠度计算，有些设计师习惯了从系统等效失效率[12]出发，继续使用指数模型计算系统的可靠度。其实，这是有失偏颇的，因为备份后系统的整体寿命分布已经不再符合指数模型。本文分别从由两个单元(单元失效率符合指数分布)组成的热备和冷备系统出发，对比了采用等效失效率和概率法两种方法计算得到的冗余系统的可靠度。

1 无备份系统的可靠度

1.1 指数分布

经过长期实践发现，电子元器件基本都服从一条典型的失效率曲线，即“浴盆曲线”[11]。失效率可以划分为三个阶段：早期失效期、偶然失效期和耗损失效期。

第一阶段早期失效期：开始使用时，失效率很高，但随着工作时间的增加，失效率迅速降低。失效的主要原因是设计、制造等缺陷。第二阶段偶然失效期，也称随机失效期：失效率较低且稳定，近似为常数。失效的主要原因是质量缺陷、环境和使用不当等。第三阶段耗损失效期：失效率随时间的增加迅速上升。失效的主要原因是磨损、老化和耗损等。

图1 浴盆曲线

一般电子元器件经过老炼筛选后，都处于偶然失效期，基本失效率近似为常数，即遵从负指数分布规律。以串联系统为例，传统方法采用了如下的可靠性预计公式

(1)

式中N为串联元器件的个数，t为工作时间，λi为第i个元器件的基本失效率，可由元器件计数法或应力分析法给出。

1.2 无备份系统可靠度计算

为了便于讨论，考虑两个不同单元(无备份)组成的串联系统，其可靠性框图见图2。设两个单元的可靠度和失效率分别为rA、λA和rB、λB，两个单元的寿命分布均符合指数模型r=e-λt。

图2 串联系统(无备份)可靠性框图

根据概率法，串联系统的可靠度Rs为各单元可靠度的连乘，此时系统的可靠度计算为

(2)

可以看到，在无备份的情况下，整个系统仍然满足指数分布，系统等效失效率为

(3)

2 备份系统的可靠度

2.1 热备系统可靠度计算

设有一个由两相同单元组成的热备系统，其中至少一个单元工作时，系统就能正常工作，其可靠性框图如图3所示。设每个单元的可靠度和失效率均为r和λ，每个单元的寿命分布符合指数模型r=e-λt。

图3 两单元热备系统可靠性框图

根据概率法和表决模型，可以求得系统可靠度Rs1为

(4)

显然，此时系统可靠度已不满足指数分布。

对于此热备系统，系统的平均无故障工作时间(MTBF)为

(5)

系统的等效失效率λs定义为系统的平均无故障工作时间(MTBF)的倒数[12]，即

(6)

因此，此热备系统的等效失效率为

(7)

(8)

2.2 冷备系统可靠度计算

图4 两单元冷备系统可靠性框图

设有一个由两相同单元组成的冷备系统，其可靠性框图如图4所示。设每个单元的可靠度和失效率均为r和λ，每个单元的寿命分布符合指数模型r=e-λt，考虑检测装置和转换开关完全可靠的情况，系统的可靠度Rs2为[9]

(9)

显然，和热备系统一样，此时冷备系统可靠度也不再满足指数分布。

对于此冷备系统，系统的平均无故障工作时间(MTBF)为

(10)

因此，系统的等效失效率为

(11)

(12)

3 计算结果分析

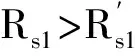
图5 两单元热备系统可靠度计算(红色实线代表公式(4)，蓝色虚线代表公式(8))

图6 热备系统可靠度采用指数模型产生的误差

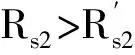
图7 两单元冷备系统可靠度计算(红色实线代表公式(9)，蓝色虚线代表公式(12))

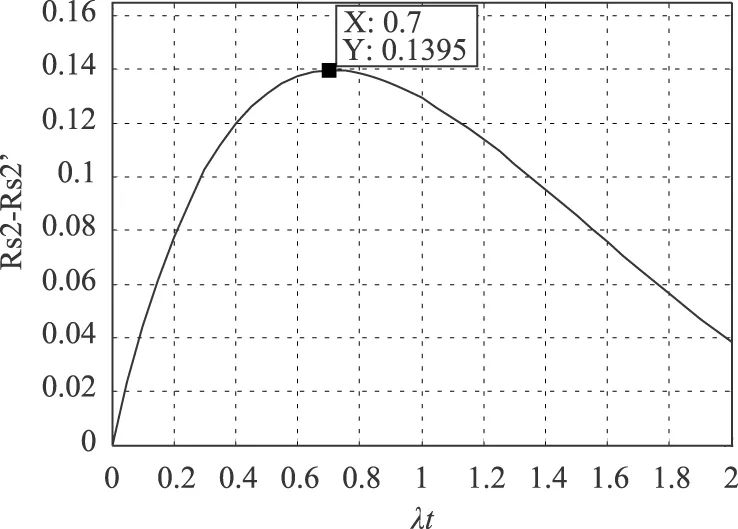
图8 冷备系统可靠度采用指数模型产生的误差

4 结 语

理论计算表明服从指数分布的单元构成的系统，其系统失效率在没有冗余备份的情况下仍然服从指数分布。但系统采取冗余备份后(以两个单元为例)，无论是热备还是冷备，如果仍使用等效失效率按照指数模型来计算系统可靠度，计算值将比实际值明显偏低。本文指出了两种方法计算两单元构成的冗余系统可靠度的差异，为系统可靠性预计提供了参考。本文发现的计算方法所带来的误差，对于多个单元构成的表决系统以及其它复杂的旁联模型，需要进一步探讨。

[1] 曾利伟,吕川.可靠性预计方法及思考[J].可靠性分析与研究，2005,9:28-30.

[2] 陈亚兰,罗俊,李晓红.电子装备可靠性预计方法概述[J].微电子学，2013,43(2):242-249.

[3] 张友兰,王杰.大型电子系统可靠性分析及评估方法研究[J].中国电子科学研究院学报,2016,8(5):464-469.

[4] 胡映.系统可靠性预计的方法[J].现代电子技术,2003,1:13-15.

[5] 杜肖,高飞.航空装备可靠性预计中可靠性数据的来源分析[J].测控技术,2015,34:680-682.

[6] 李亦非,王文静,等.电子式电能表可靠性预计及验证分析[J].现代电子技术2011,34(22):141-143.

[7] 章治本.转换开关不完全可靠的热贮备系统可靠性模型[J].中国电子科学研究院学报,2016,1(1):39-43.

[8] 莫兰英,表决系统及其相关问题的可靠性分析[D].长沙:长沙理工大学,硕士学位论文,2009.

[9] 李玲.两部件冷备系统可靠性的统计分析[D].上海:华东师范大学,硕士学位论文,2009.

[10]郭维长.可靠性预计中的置信度问题研究[J].中国空间科学技术,2002,6:13-17.

[11]郭青,宁磊.无线通信产品的可靠性预计与实现[J].现代电子技术2013,36(18):7-12.

[12]张增照.以可靠性为中心的质量设计、分析和控制[M].电子工业出版社,北京,2010.

The Reliability Prediction of the Standby System Composed of Two Component

WANG Jian, DING Bang-zhou

(No. 38 Research Institute of CETC, Hefei 230088, China)

The reliability of standby system (including hot standby system and cold standby system) composed of two components was discussed through equivalent failure rate and probability method, respectively. The result showed a considerable error. The numerical value based on equivalent failure rate and exponential distribution was lower. The result indicated the reliability of standby system did not follow exponential distribution any more. This paper was helpful for the reliability prediction of large electronic equipment.

standby system; failure rate; exponential distribution; reliability prediction

10.3969/j.issn.1673-5692.2017.04.018

2017-03-01

2017-07-01

汪 建(1986—)，男，博士，工程师，主要研究方向为星载SAR系统设计、可靠性设计；

E-mail：hswj@mail.ustc.edu.cn

丁邦宙(1973—)，男，博士，工程师，主要研究方向为可靠性工程与质量管理。

TP302.8

A

1673-5692(2017)04-428-04