改进的快速扩展随机树路径规划算法*

孙丰财， 张亚楠， 史旭华

(宁波大学 信息科学与工程学院,浙江 宁波 315000)

改进的快速扩展随机树路径规划算法*

孙丰财， 张亚楠， 史旭华

(宁波大学 信息科学与工程学院,浙江 宁波 315000)

针对快速扩展随机树(RRT)路径规划算法缺乏稳定性和偏离最优解的问题，提出了一基于RRT的偏向性路径搜索算法(m-RRT)。m-RRT采用生成随机点向量组的形式对随机点选取策略进行了优化，改善快速扩展随机树的不确定性，减少不必要的扩展，而加快向目标位置搜索的速度，且得到的路径优于RRT算法的结果。通过其在二维平面路径规划和三维机械臂路径规划的测试,表明其具有一定的应用价值。

路径规划； 机械臂； 快速扩展随机树算法； 避障； 机器人操作系统

0 引 言

机器人路径规划即通过某些性能(如时间、距离、能量)指标来规划出一条从初始位置到目标位置的最优或者较优的线路。目前，机械臂路径规划方法主要有细胞分解法、人工势场法、随机路标法(probabilistic roadmap，PRM)和快速扩展随机树(rapidly-exploring random tree，RRT)法等[1～3]。

针对传统RRT算法的缺陷，Burget F，Bennewitz M等人[4]采用双向随机搜索树(Bi2RRT) 搜索算法，提高了搜索效率，由于该算法较原始RRT算法有更好的收敛性，因此，在目前路径规划中很常见。Melchior N A[5]提出的粒子RRT算法考虑了地形的不确定性，保证了在不确定性环境下随机搜索树的扩展。Kuffner J J等人[6]提出了RRT2connect算法，使得节点的扩展效率大大提高；同时王道威等人[7]采用动态步长改善了RRT的不确定性，冯林等人[8]通过对比优化的方法使得在复杂环境下的规划稳定性增强，宋金泽等人[9]通过添加非完整性约束及双向多步扩展方式提高了搜索效率。

本文针对RRT算法搜索缺乏稳定性和偏离最优解等缺点，对RRT算法进行了相应的改进，通过实验发现改进算法在二维环境和三维环境均能取得较好的效果。因此,算法对二维、三维环境的路径规划，尤其是机械臂的路径规划具有一定的参考价值。

1 RRT算法流程

1.1 RRT算法

以节点qstart为初始点，qgoal为目标点，建立搜索树T，其初始化和扩展过程步骤如下:

1)选择初始点qstart为根节点。

2)在位形空间中随机选取采样点qrand。

3)在已经产生的搜索树上，搜索一个距离采样点qrand最近的节点qnearest。

4)在qnearest和qrand的连线上，以一定的步长r从qnearest出发创造一个新的节点qnew。如果从qnearest到qnew的扩展过程中无碰撞发生，则将这个新的节点qnew加入到搜索树中，并同时将从qnearest到qnew的边插入到搜索树中；反之，则无扩展发生。

重复上述步骤，在用户定义约束的限制下，不断计算qnew与qgoal的距离，直至其小于给定的距离阈值。

图1 RRT算法核心步骤

RRT算法的随机采样扩张特性，导致其收敛到目标点位置的速度比较慢，耗费的空间资源比较大，同时搜索出的路径往往偏离最短路径；为了提高算法的效率和性能，需不断对该算法进行改进。

1.2 改进后的RRT算法

针对扩展节点的选取，提出了改进RRT算法，即m-RRT算法。

首先，m-RRT算法采用大多数变异RRT算法的通用策略，在标准的RRT算法基础上加入了偏向策略，即在一定的小概率情况下将随机采样节点qrand设置为目标点，以促进搜索因子尽快趋向目标点，以提高搜索效率。

其次，与标准RRT算法步骤(2)不同，m-RRT算法每次随机采样m个节点，按照与目标点的距离排序构成随机序列，将距目标点最近的点作为随机点qrand开始探索，如果发现发生碰撞导致无法扩展，则需取次距离点进行计算；当随机序列中首次未碰撞的节点执行完成，或者随机序列为空之后再次随机生成m个采样节点，继续上述步骤。

算法减少了不必要的探索方向，一定几率地减少了再次遇到障碍物的可能性，保留了对目标位置的全局趋向性；同时，依次尝试保证了节点有能力跳出障碍区域，避免陷入局部，有利于快速寻找到目标点。本文通过实验对比m-RRT算法的搜索时间效率和结果路径优劣性，选择每轮随机采样个数m=4，此时算法性能表现良好。m-RRT算法主要流程如下：

1)初始化起点qstart和目标点qgoal并在位形空间内建立障碍物模型。

2)在位形空间中随机选取采样点qrand,并扩展新生成节点qnew直至到达目标节点qgoal。

a.在空间中随机采样4个位置节点，并按照离目标点的距离排序存入qrand_arr随机序列，选取离目标点距离最近点设为节点qrand。

(1)

机械臂距离公式(各关节角度距离其目标角度之和)

(2)

b.按照标准RRT算法步骤选择随机树T中离随机采样点qrand最近的节点为qnearest，按照一定步长进行生成扩展节点qnew，同时检测从节点qnearest到节点qnew是否与障碍物发生碰撞，如果发生碰撞，则在随机采样点qrand_arr随机序列中选择次位的节点成为新的随机节点qrand。

3)如果没有发生碰撞则在此方向继续扩展节点并收入随机树中，继续沿此方向扩展，直至发生碰撞，此时，舍弃随机序列qrand_arr，重新生成4个随机点构成新的随机序列。

4)当目标点qgoal与新生成的节点qnew距离小于或等于步长时，将qnew=qgoal，此时如无碰撞则程序结束，若有碰撞则继续步骤(2)。

5)将得到的路径点进行保存，得出结果。

改进后算法在二维平面路径规划中可以大量减少规划时间，并且整棵树的生长偏向于目标点，随着树的生长更容易找出更好的路径；在三维空间中，不需耗费巨大的空间资源，同时，m-RRT算法由于树的趋向性生长避免了对许多无意义空间的探索，减少了标准RRT算法执行时间，相比于RRT-Start等追求接近最优解的算法，其规划结果也很理想。

2 实验对比

2.1 二维有障碍环境下算法效果

2.1.1 简单环境下算法比较

如图2所示，实验分别对piz-RRT算法[10]、标准RRT算法、RRT-star算法[11]、m-RRT算法进行了比较，其中m-RRT算法给出了当随机序列节点数m取值分别为2，4，6时的运行效果。演示图均为左侧圆形点位置为起始点右侧圆形点位置为目标点进行规划。在简单环境下，对比4种算法效果发现m-RRT算法扩展节点大量减少，树的生成有一种趋向性，空间资源浪费很少；同时通过不同随机序列节点数m的取值，可以明显发现规划路径慢慢趋向于稳定和更优化。

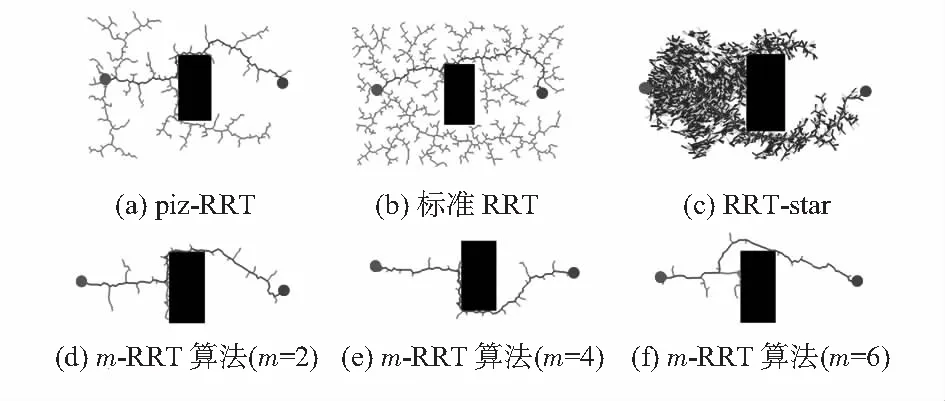
图2 简单环境下4种算法比较

2.1.2 复杂环境下算法比较

复杂环境中，不仅障碍物数量增多，起始点与目标点也不易直接搜寻，很大程度提高了路径规划的难度。如图3所示，同样将以上4种算法进行比较，其中，m-RRT算法给出了当随机序列节点数m分别取值为2，4，6时的运行效果。演示图均为左侧圆形点位置为起始点，右侧圆形点为止为目标点进行规划。通过对比可以发现即使环境变得复杂，m-RRT算法依然能够利用很少的扩展到达目标位置，不仅消耗空间资源少，规划路径也具有明显的优势。

图3 复杂环境下4种算法比较

通过以上实验可以发现：对于m-RRT算法，不同m的取值使得规划路径慢慢趋向于稳定和更优化，但经过对比发现这种路径的优化是通过牺牲时间效率达到的，并且当m节点数增加太多也会使m-RRT算法的优势降低，通过综合对比最终选用m=4，此时路径规划算法无论规划结果或者规划耗时均较为满意，视为最佳方案。

2.1.3 二维路径规划效率对比

以上实验的4种算法中，从耗费空间资源的角度，RRT-star算法和标准RRT算法耗费最多，而m-RRT算法与piz-RRT算法相差不多，相比前两者，在空间资源的消耗上有明显的优化，付出的空间代价很小。从规划结果来看，其他3种算法的随机性较m-RRT算法强，m-RRT算法很大程度上降低了随机程度。同时，通过表1中所示的5种不同环境下(从第一组到第五组障碍物依次增多)，4种算法的路径规划耗时对比，可以看出：RRT-star算法时间复杂度成倍提升，其次为标准RRT算法，这两者在时间的消耗上远大于piz-RRT和m-RRT算法。可见，随着环境复杂度的增大，m-RRT也同样获得了很好的效果。实验证明了m-RRT算法规划出的路径更趋向于平稳，在大多数情况下优于其他3种算法，且规划路径较为紧凑，也更接近于理想路径。

表1 4种改进RRT算法效率对比 s

2.2 三维有障碍环境下机械臂路径规划算法效果

2.2.1 机械臂路径规划演示

如图4所示为运用m-RRT算法的路径规划运行效果。图(a)中绿色机械臂为起始位置，橘色机械臂代表目标位置，图4(b)～图4(f)依次给出了一次规划的结果，整体运行路线如图4(g)和图4(h)所示。可以看出：在有障碍物的环境下运用m-RRT算法能够完整地解决此类路径规划问题，将机械臂移至侧面的行为完全没有接触到障碍物，并且机械臂先运动到上方，依次顺着箱体表面移动到下方，效果理想，证明了m-RRT算法在三维机械臂的路径规划中的有效性。

图4 三维环境下改进算法路径规划结果

2.2.2 机械臂路径规划效率对比

图5所示为2种不同三维环境下标准RRT算法和m-RRT算法的效率比较，分为不同组别，每组取平均值进行比较，可以看出：在障碍物较多的情况下2种RRT算法在解决路径规划问题的效率有较大差异，标准RRT算法耗时较多且并不稳定，m-RRT算法相对更加稳定，且不论环境是否复杂，其执行效率相对优越。同时，在三维机械臂路径规划实验中发现RRT-star等算法效率较差，耗时过久且时常无法找到解，并不适用于此类规划。

图5 复杂环境和简单环境情况下效率对比

3 结束语

通过以上二维平面和三维机械臂路径规划研究发现，m-RRT算法明显提高了RRT路径规划的稳定性，并且有利于规划出接近于最优路径的较优路径，相对于标准RRT算法，其效率更高，无论在算法效率还是路径质量，均体现出了很大的优越性。同时m-RRT算法在三维机械臂路径规划上也能够取得较好的效果。实验表明：m-RRT算法在路径规划上具有一定的应用价值。

[1] 王海英,蔡向东,尤 波,等.基于遗传算法的移动机器人动态路径规划研究[J].传感器与微系统,2007,26(8):32-34.

[2] 王春华,邱立鹏,潘德文.改进蚁群算法的机器人焊接路径规划[J].传感器与微系统,2017,36(2):75-77.

[3] 张云峰,马振书,孙华刚，等.基于改进快速扩展随机树的机械臂路径规划[J].火力与指挥控制,2016,41(5):25-30.

[4] Burget F,Bennewitz M,Burgard W.BI^2RRT:An efficient sampling-based path planning framework for task-constrained mobile manipulation[C]∥IEEE/RSJ International Conference on Inteligent Robots & Systems,2016.

[5] Melchior N A,Simmons R.Particle RRT for path planning with uncertainty[C]∥IEEE International Conference on Robotics & Automation,2007:1617-1624.

[6] Kuffner J J,Lavalle S M.RRT-connect:An efficient approach to single-query path planning[C]∥IEEE International Conference on Robotics & Automation,2000:995-1001.

[7] 王道威,朱明富,刘 慧.动态步长的RRT 路径规划算法[J].计算机技术与发展,2016,26(3):105-107.

[8] 冯 林,贾菁辉.基于对比优化的RRT路径规划改进算法[J].计算机工程与应用, 2011,47(3):210-213.

[9] 宋金泽,戴 斌,单恩忠,等.一种改进的RRT路径规划算法[J].电子学报,2010,38(s1):225-228.

[10] 徐 娜,陈 雄,孔庆生,等.非完整约束下的机器人运动规划算法[J].机器人,2011,33(6):666-672.

[11] Islam F,Nasir J,Malik U,et al.RRT-smart:Rapid convergence implementation of RRT towards optimal solution[C]∥International Conference on Mechatronics and Automation,2012:1651-1656.

史旭华，女，通讯作者，教授，硕士生导师，主要从事模式识别与智能算法的研究工作，E—mail:928111455@qq.com。

Improved rapidly-exploring random tree path planning algorithm*

SUN Feng-cai， ZHANG Ya-nan， SHI Xu-hua

(College of Information Science and Engineering,Ningbo University,Ningbo 315000,China)

Because the rapidly-exploring random tree(RRT)path planning algorithm is unstable and not optimal,propose a biased path search strategy which is calledm-RRT.By generating a random point vectors to optimize the strategy of random points selection,the uncertainty of RRT searching can be improved,meanwhile,the expansion of searching tree can also be reduced.So,it can improve the searching speed to the destination,and the path got bym-RRT is better than that by RRT.Through the two-dimensional path planning and three-dimensional manipulator path planning,the results show that it has certain application value.

path planning;manipulator; rapidly exploring random tree(RRT)algorithm; obstacle avoidance; robot operating system(ROS)

10.13873/J.1000—9787(2017)09—0129—03

2017—07—12

浙江省自然科学基金资助项目 (LY14F030004)；浙江省科技计划资助项目 (2015C31017)；宁波市自然科学基金资助项目(2016A610092)

TP 24

A

1000—9787(2017)09—0129—03

孙丰财(1992-)，男，硕士研究生，研究方向为模式识别与智能算法。