基于混沌的萤火虫改进粒子滤波算法研究*

朱 超， 刘以安， 薛 松

(1.江南大学 物联网工程学院，江苏 无锡 214122； 2.中国舰船研究院，北京 100192)

计算与测试

基于混沌的萤火虫改进粒子滤波算法研究*

朱 超1， 刘以安1， 薛 松2

(1.江南大学 物联网工程学院，江苏 无锡 214122； 2.中国舰船研究院，北京 100192)

针对常规的粒子滤波算法存在粒子权值退化和采样粒子贫化以及需要大量粒子才能进行比较准确的状态估计的问题，提出了一种基于混沌的萤火虫改进粒子滤波算法。利用混沌系统所具有的遍历性和随机性初始化粒子群，使得初始粒子分布更加均匀，同时向常规粒子滤波算法中引进萤火虫算法的寻优机制，使得粒子能够向高似然区域运动，提高了滤波精度，并对部分权值优秀粒子进行混沌细搜索，对部分权值低的粒子进行再生，提高了种群多样性。实验表明：该方法尤其是在粒子种群数量较小的情况下，较常规粒子滤波精度更高，并有效地改善了权值退化和样本贫化问题。

混沌优化； 萤火虫算法； 粒子滤波； 权值退化

0 引 言

粒子滤波(particle filtering,PF)是一种基于蒙特—卡罗思想的贝叶斯滤波技术[1]。常规粒子滤波经过多次迭代后，小权值粒子会发生权值退化，同时重采样仅复制大权值的样本，又会导致粒子样本贫化。

针对粒子滤波的权值退化和样本贫化问题，文献[2]提出了一种改进权值选优粒子滤波，一定程度上改善了权值退化问题。文献[3]提出了一种加权逼近的粒子滤波算法，缓解了权值退化，但在多次迭代后容易导致样本贫化。文献[4]提出了基于权值选择的粒子滤波，通过对预测粒子集样本进行预处理来增加样本有效数，但容易导致权值的退化。文献[5]提出了一种萤火虫智能优化粒子滤波(firefly algorithm intelligence optimized particle filtering,FA-PF)算法，引进了萤火虫寻优机制，然而对小权值的样本吸引小，容易导致粒子权值退化。

本文通过在常规粒子滤波框架下引入萤火虫算法寻优机制，并利用混沌的遍历性、随机性的特点进行优化，用混沌序列初始化种群，使得初始粒子能够更加平均地接近真实状态[6]。对优秀的萤火虫进行混沌细搜索，对相对较差的萤火虫进行随机再生，从而在一定程度上保持了样本的多样性，减轻粒子权值退化程度，增加了滤波精度，尤其在粒子数较少的情况下，通过算法验证，能够得到更高的滤波精度和稳定性，从而减少了迭代次数和运算量。

1 粒子滤波算法

假设非线性系统的状态方程和观测方程如下

(1)

式中 xk为状态值；yk为观测值；vk-1和wk分别为过程噪声和量测噪声。若初始概率密度为p(x0|y0)=p(x0)，则状态方程的预测方程为

(2)

状态更新方程为

(3)

设重要性函数为q(x0∶k-1|y1∶k)，则权值公式为

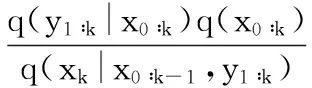
(4)

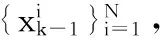
(5)

式中 δ(·)为狄拉克函数。

概率密度更新公式为

(6)

最后进行权值归一化，并输出状态

(7)

(8)

2 萤火虫算法

算法描述:萤火虫被比其亮度大的萤火虫所吸引；萤火虫的吸引度和亮度成正比，亮度随着距离的增加而减少；如果没有一个比其自身更亮的萤火虫，将随机移动。算法主要参数描述如下：

1)萤火虫相对亮度为

I=I0×e-γrij

(9)

式中 I0为最大荧光亮度; γ为光强吸收系数;rij为两萤火虫的空间距离。

2)萤火虫吸引度为

β=β0×e-γrij

(10)

式中 β0为最大吸引度。

3)萤火虫位置更新为

xi=xj+β(xi-xj)+α×(rand-0.5)

(11)

式中 xi,xj为萤火虫位置;α为步长因子;rand为[0,1]上服从均匀分布的随机数[7]。

3 混沌优化策略

文献[8]对不同的混沌映射算法进行了性能分析。其中，Kent混沌映射在区间(0,1)具有更加优秀的遍历均匀性。Kent混沌映射的数学表达式为

(12)

混沌优化策略：将待优化值映射到混沌空间(0,1)上，代入式(12)得到混沌序列，再将混沌序列按照尺度变换还原到解空间中，重新计算函数值，如果出现更优的解，则该解替代原解[9]。为了提高搜索效率，可以根据式(13)动态收缩搜索区域

(13)

式中 [xmin,j,xmax,j]为第j维变量的搜索范围；xg,j为当前的最优值；ρ为搜索因子

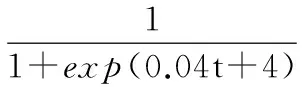
(14)

式中t为当前搜索次数。

4 混沌萤火虫优化粒子滤波算法

4.1 优化策略

本文算法以粒子滤波作为滤波框架，使用Kent混沌初始化粒子群，使得初始的粒子能够更加均匀地分布在真实解周围。通过引进萤火虫寻优机制，吸引粒子进行寻优运动，并在萤火虫寻优过程中对优秀的粒子进行混沌细搜索，对劣等的粒子进行随机重生。然而传统的萤火虫算法由于在位置更新时需要各粒子间交互作用，会严重影响滤波的算法复杂度和滤波时间。针对这个问题，本文借鉴了粒子群智能算法的思路，设置全局最优值，将各个迭代时刻的粒子目标函数与最优值进行比较，得到一个全局最优值，并不断更新该值，用全局最优值替代j和i萤火虫进行信息交互。本文对萤火虫算法进行了改进，更新如下：

1)修正萤火虫荧光亮度公式

(15)

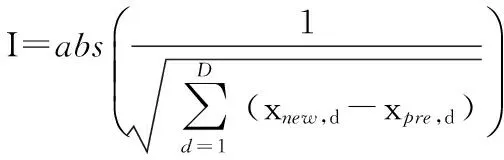
(16)

式中d为第d维。

2)修正萤火虫吸引度公式

β=β0×e-γr2i

(17)

式中ri为粒子i与全局最优值gbestk之间的欧氏距离。

3)修正萤火虫位置更新公式

(18)

4.2 算法实现步骤

1)随机产生一个(0,1)之间的随机数，代入式(10)求得N-1个混沌序列，将长度为N的混沌序列变换到解空间中作为初始粒子。

2)模拟萤火虫优化过程，更新粒子位置。

由式(17)计算粒子i与全局最优值之间的吸引度；根据式(18)更新粒子位置。

3)将前10 %亮度的萤火虫作为优秀粒子进行混沌细搜索优化，将亮度后10 %的萤火虫作为劣质粒子用随机产生新的萤火虫替代。

4)计算新的萤火虫种群的亮度值，更新全局最优值

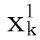
(19)

5)若达到终止阈值ε或者最大迭代次数MaxGeneration，则算法迭代结束；否则，转入步骤(2)。

6)由于每个粒子均进行了寻优移动，分布密度函数出现了变化，需要进行权值补偿更新

(20)

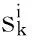
7)权值按式(7)进行归一化。

8)将归一化后的权值以及优化后的粒子代入式(9)计算状态输出。

5 仿真实验

实验硬件条件为inteli5—4200H处理器，12GB内存，软件环境为Matlab2014b，仿真的状态模型和观测模型

(21)

式中v(k)和w(k)选取零均值高斯白噪声；系统噪声方差Q=1；量测噪声方差R=1。在萤火虫算法中参数设置参考现有文献的通常参数，最大吸引度为1，步长因子为0.3，最大光强吸收系数为1。

本文利用PF和CFA—PF算法进行实验评估，其中，均方根误差公式为

(22)

(23)

式中 Neff为有效粒子数；round()函数为向最近的整数取整运算[10]。

5.1 精度测试

取N=20，Q=1，结果如图1(a);取N=100，Q=1，结果如图1(b)。

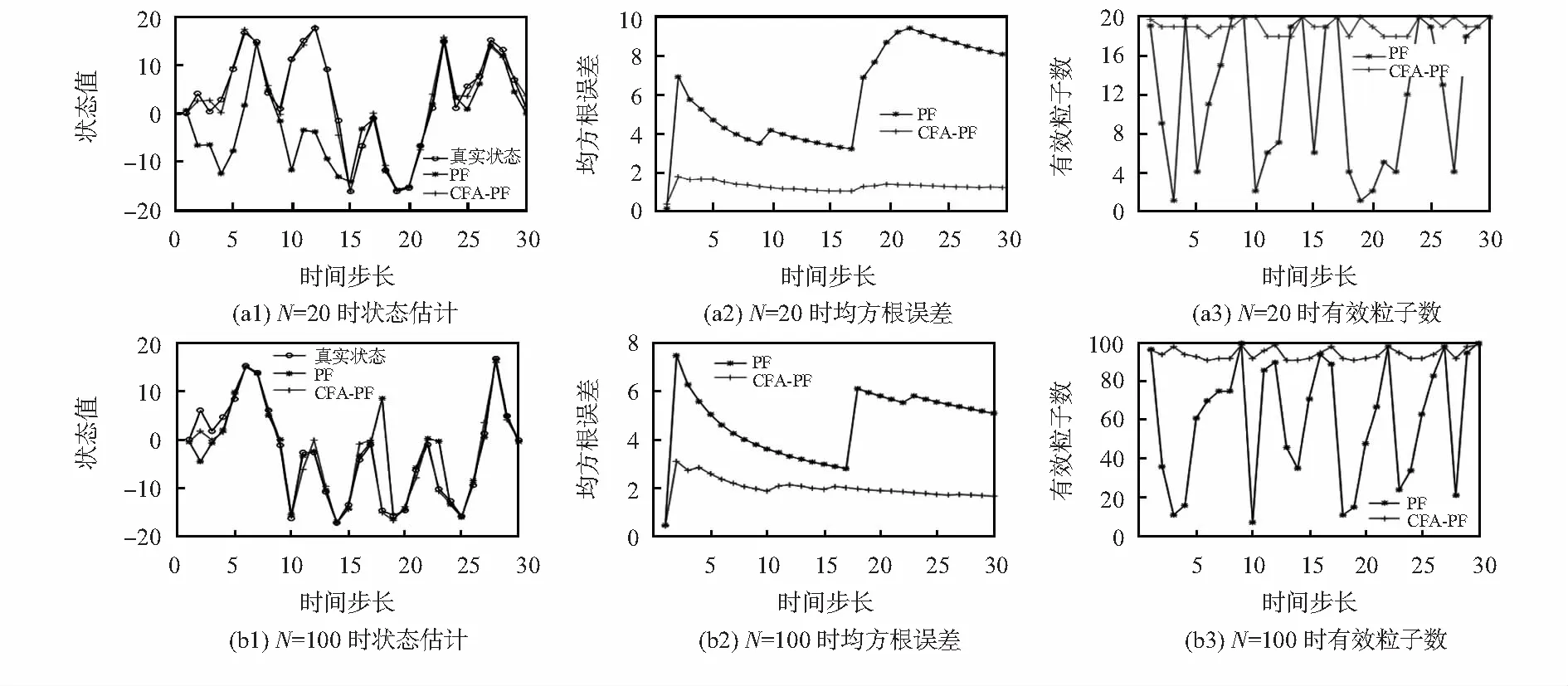
图1 N=20和100时PF算法和CFA—FA算法测试结果

从图1可以看出：相对于标准的PF算法，CFA—FA算法在粒子数较少的情况下，均方根误差要明显小于PF算法，说明滤波精度优于PF算法，且CFA—FA算法的有效粒子数明显高于PF算法，也更加稳定，可见CFA—FA算法可以有效地改善粒子权值退化问题。

5.2 粒子多样性测试

取N=100，滤波器在t=30时刻的粒子分布情况如图2所示。

图2 k=30时粒子状态分布情况

从图2中可以看出：PF算法的粒子样本发生贫化，而CFA—PF算法在低似然区域也保留了部分粒子，从而保证了样本多样性。

6 结 论

吸取了传统粒子滤波的优点，引入了混沌优化策略，同时将萤火虫算法进行改进，减少了常规的FA算法的运算复杂度，并将改进的萤火虫算法融合到粒子滤波当中，实验结果证明：其有效地提高了滤波精度，尤其在粒子比较少的情况下，滤波精度明显高于常规的FA算法，同时改善了粒子权值的退化，并保持了一定的粒子多样性。

[1] 李天成,范红旗,孙树栋.粒子滤波理论、方法及其在多目标跟踪中的应用[J].自动化学报,2015(12):1981-2002.

[2] 刘 刚,彭 力.权值选优粒子滤波的无线传感器网络目标跟踪[J].传感器与微系统,2011,30(6):30-32，35.

[3] 宁小磊,王宏力,徐宏林，等.加权逼近粒子滤波算法及其应用[J].控制理论与应用,2011(1):118-124.

[4] 张 琪,胡昌华,乔玉坤.基于权值选择的粒子滤波算法研究[J].控制与决策,2008(1):117-120.

[5] 田梦楚,薄煜明,陈志敏，等.萤火虫算法智能优化粒子滤波[J].自动化学报,2016(1):89-97.

[6] 彭珍瑞,赵 宇,殷 红，等.基于混沌猴群算法的传感器优化布置[J].传感器与微系统,2014,33(10):104-107.

[7] 程美英，倪志伟，朱旭辉.萤火虫优化算法理论研究综述[J].计算机科学,2015，42(4):19-24.

[8] 苏有良,周德俭,吴兆华，等.不同映射的混沌免疫进化算法性能分析[J].计算机工程,2010,36(21):222-224.

[9] 王尔申,庞 涛,曲萍萍，等.基于混沌的改进粒子群优化粒子滤波算法[J].北京航空航天大学学报,2016(5):885-890.

Research of improved particle filtering algorithm for fireflies based on chaos*

ZHU Chao1， LIU Yi-an1， XUE Song2

(1.College of IOT Engineering,Jiangnan University,Wuxi 214122,China; 2.China Ship Research and Development Academe,Beijing 100192,China)

Aiming at problem exists in conventional particle filtering algorithm of particle weight degradation and sampling particle impoverishment and it needs for a large number of particles to achieve accurate state estimation a firefly improved particle filtering algorithm based on chaotic is proposed.By using the ergodic and random initialization particle swarm of the chaotic system,the initial particle distribution is more uniform.At the same time,the optimization mechanism of the firefly algorithm is introduced into the conventional particle filtering algorithm,which can make the particles move to the high likelihood region,so as to improve the precision of the filtering.Using chaos search on the part of the weight of the excellent particle at the same time,and regenerate part of low weight particles,to achieve demand of diversity of improving population.Experiments show that this method is more accurate than the conventional particle filtering,especially in the case of small populations,and effectively improve the weight degeneracy and sample impoverishment problem.

Chaos optimization; firefly algorithm; particle filtering; weight degeneracy

10.13873/J.1000—9787(2017)09—0106—04

2016—06—20

国家自然科学基金资助项目(61170120)

TP 391

A

1000—9787(2017)09—0106—04

朱 超(1990-)，男，硕士研究生，主要研究方向为电子对抗和数据融合。

刘以安(1962-)，男，硕士生导师，主要从事电子对抗和数据融合的研究工作。