非稳态Couette流动阶段的边界位移与黏性能量耗散
闫 彦
(中国石油化工集团公司发展计划部,北京100728)
非稳态Couette流动阶段的边界位移与黏性能量耗散
闫 彦1)
(中国石油化工集团公司发展计划部,北京100728)
本文研究了牛顿流体非稳态Couette流动阶段的边界位移与流体黏性摩擦能耗.在上边界始终保持静止,下边界以恒定速度或恒定内壁剪切应力突然运动的情况下,建立了 Couette非稳态流动的数学模型.求解定解问题,获得流体速度分布函数;通过渐近分析,获得不同边界条件下流动充分发展的临界时间,进而获得非稳态过程中的边界位移量.利用边界剪切应力和位移量的结果,计算非稳态过程中移动平板做功;再结合流体动能增加量,计算得出不同边界条件下非稳态流动阶段流体黏性摩擦能耗.
边界位移,能量耗散,非稳态阶段,Couette流动
Couette流动是流体力学的经典问题,是指黏性流体在相对运动着的两平行平板之间的层流流动.流体处于静止状态时,平板突然运动会引起非稳态Couette流动.对于平板速度恒定的非稳态Couette流动,已经有学者开展了大量研究,并得出了速度分布随时间变化的解析解[12].基于经典黏性流体非稳态Couette流动研究结果,许多学者针对特殊流体或特殊工况开展了进一步研究,如考虑压力梯度的非稳态Couette流动[3],非牛顿流体的非稳态Couette流动[45]以及电磁场[6]或多孔介质空间内的非稳态Couette流动[7].但上述研究中,均将Couette流动中移动边界定为控制速度边界.也有学者针对其他类型的边界条件开展了相应研究,Ting[8]通过控制恒定的壁面剪切应力,研究了二阶流体非稳态Couette流动;Bernardin等[9]则通过控制 Taylor-Couette系统的扭矩,开展了内部流体非稳态流动过程研究.
上述关于非稳态Couette流动的研究,通常更关注流体速度分布函数的求解.Muzychka等[10]则对牛顿流体非稳态Couette流动中的非定常参数开展研究,通过寻求非稳态Couette流动与Stokes第一问题间的关联,建立了描述移动边界内表面剪切应力随时间变化的简易模型,对非定常剪切应力进行了渐近分析.然而文献[10-11]在进行渐进分析时,通常只针对恒定速度边界条件,并未考虑其它边界条件下的非稳态流动发展过程.
Couette流动被认为是流变测试的理论基础[10].对于与时间相关的黏性流体,例如胶凝原油,流变学中常通过连续记录应力与应变关系分析其力学特性[1213].然而,在初始非稳态阶段,速度分布的非线性,会造成测试结果出现偏差.两平板边界的相对位移是用来计算剪切应变的核心参数,非稳态过程中,两平行板间的相对位移越大,表明测试过程处于非稳态流动的应变范围越大.另外,流体黏性摩擦能耗会造成体系熵增,文献[13-14]以剪切能量耗散为指标衡量材料物性变化,非稳态Couette流动阶段的能量耗散过程明显不同于稳态阶段,同样值得关注.
对于类似胶凝原油的材料,常采用控制恒定剪切应力[1516]或恒定剪切速率[12]的方式开展流变测试.对于流变测试系统,恒定剪切速率即是恒定边界移动速度.所以,本文将针对相同稳定状态的Couette流动,分别在恒定速度边界、恒定剪切应力边界条件下研究非稳态阶段边界位移,寻求位移的函数表达式,分析影响位移大小的相关参数,对比不同边界条件下非稳态Couette流动阶段的边界位移量;并基于非稳态阶段的边界位移研究结果,进一步计算非稳态过程中的体系输入功,再结合流体动能增加量,获得不同边界条件下非稳态Couette流动阶段的流体黏性摩擦能量耗散.
1 问题描述
如图 1所示,初始时刻两平板及中间液体静止,平板间距为d,下平板突然运动,其边界条件分为恒定速度边界与恒定剪切应力边界.控制恒定速度边界时,下平板突然以速度u0开始运动;控制恒定应力边界时,下平板内表面突然施加剪切应力τ0.上平板始终保持静止.当t≥td,Couette流动达到稳定状态.此时,两种边界条件下流动状态一致,故剪切应力τ0与速度u0满足
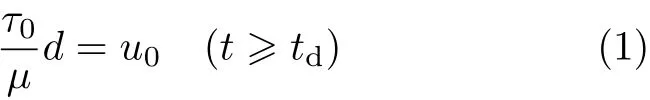
式中,td为 Couette流动达到充分发展的时刻,µ为流体的动力黏度.本文在对不同边界条件下,对0≤t≤td时间段内下平板位移、流体黏性摩擦能量耗散分别进行求解.
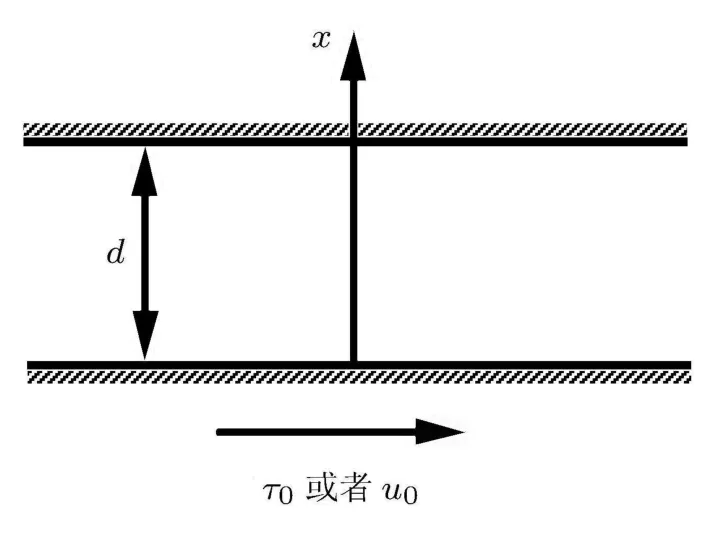
图1 Couette流动示意图
2 问题求解
2.1 恒定剪切应力边界条件下的边界位移
控制方程

其中,u表示流体流速,为空间x与时间t的函数,ν为流体的运动黏度.
(1)初始条件
初始状态,流体与平板均保持静止
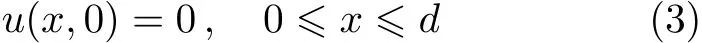
(2)边界条件
本文研究的Couette流动,两平行板中,上板始终保持静止,故
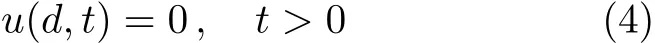
对于控制恒定应力边界,下平行板内表面剪应力τ满足
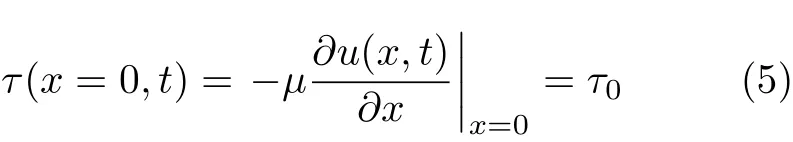
根据式(2)~式(5),可求解出速度函数为
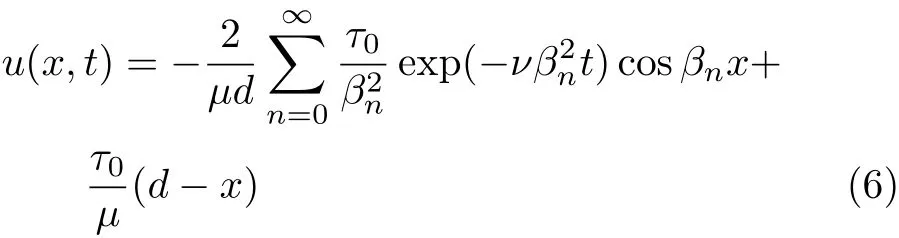
其中
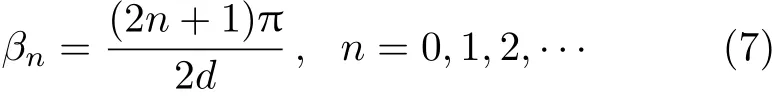
利用式(1),下平板速度可以描述为
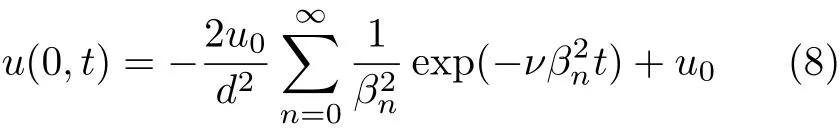
式(8)关于时间t积分,即为边界位移量.结合式(7),可获得位移表达式为
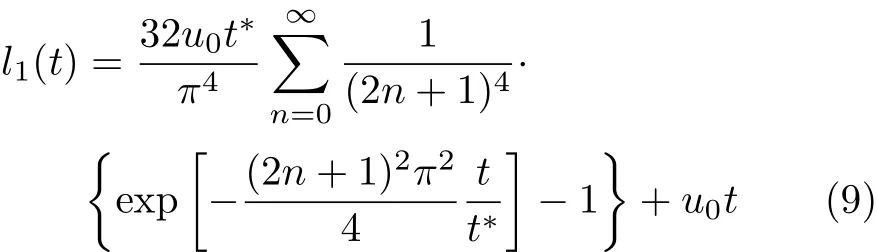
式中,l1表示恒定剪切应力τ0时不同时刻的平板位移;t∗=d2/ν为特征时间.下平板任意时刻速度与稳态速度的比值可以表示为
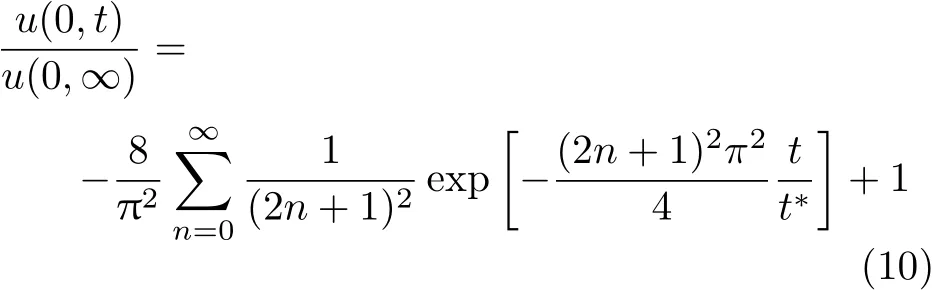
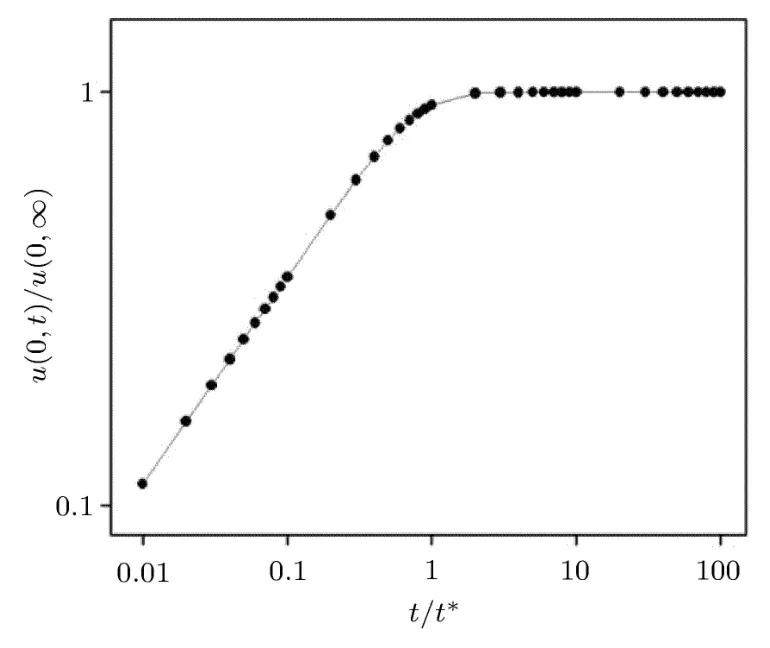
图2 恒定应力边界条件下无量纲速度的变化
从图中可以看出,恒剪切应力边界条件下,Couette流动移动边界处速度随时间从 0开始增大,并逐渐趋于稳定.本文认为,恒定剪切应力边界条件下,当边界速度u(0,t)与稳定流动状态速度u0的相对差值为0.01时,Couette流动充分发展[17],即
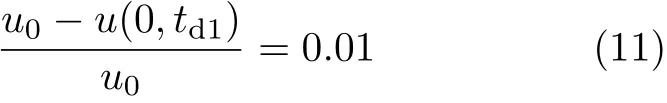
式中,td1为恒定剪切应力条件下Couette流动达到充分发展的时刻.根据式(10)、式(11),可以计算出td1=1.785t∗时,速度充分发展.结合式(9),可以计算出非稳态过程中下平板位移为
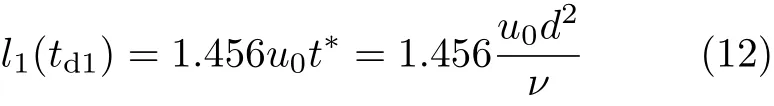
从式(12)可以看出:恒定剪切应力边界条件下,在Couette流动的初始非稳态阶段,平板边界的移动距离l1(td1)与稳态平板速度u0、特征时间t∗相关,即平板间距d、流体运动黏度ν与稳定流动时平板速度u0决定非稳态阶段的平板位移l1(td1).
2.2 恒定速度边界条件下的边界位移
对于恒定边界速度u0的情况,不同时刻边界位移可以描述为

式中,l2表示恒定速度 u0时不同时刻的平板位移.对于控制恒定速度边界的非稳态Couette流动,文献[1]已开展了相关研究,并给出了流体速度分布函数
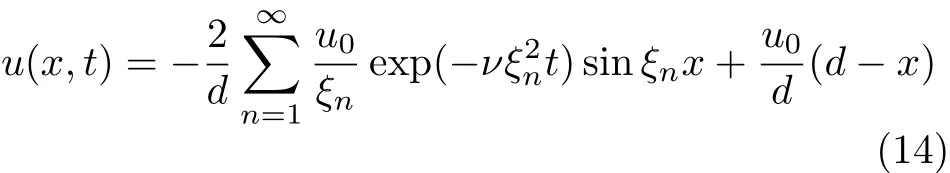
其中
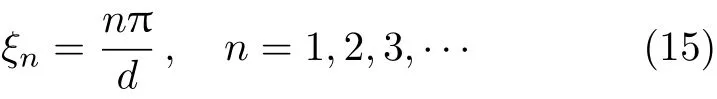
壁面处剪切速率可以表述为
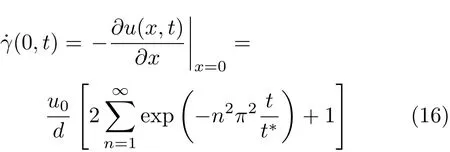
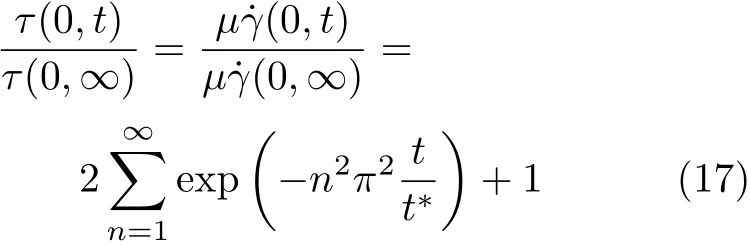
式中,τ(0,∞)表征非稳态Couette流动达到稳定后移动边界处的剪切应力;τ(0,t)为任意时刻移动边界处的剪切应力.参数τ(0,t)/τ(0,∞)随t/t∗的变化规律,如图3所示.
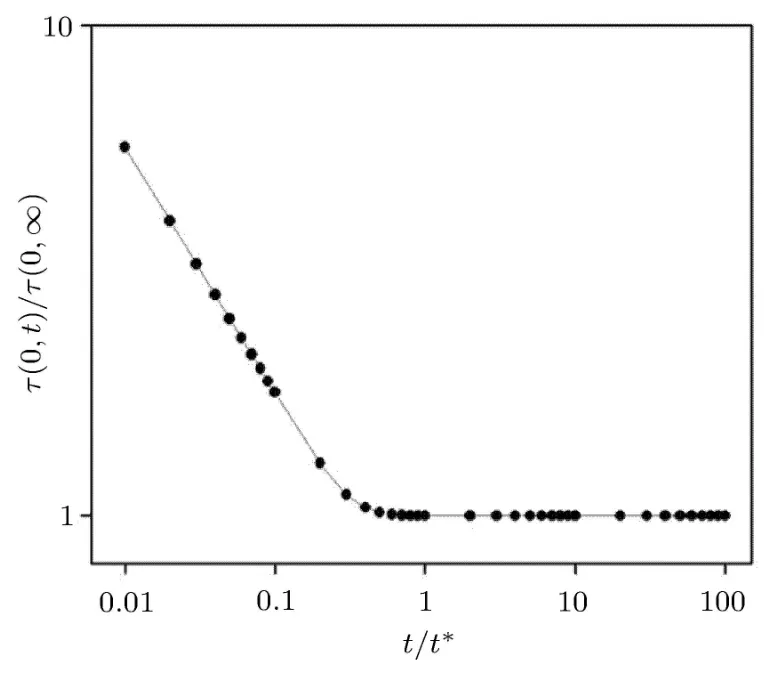
图3 恒定速度边界条件下的无量纲剪切应力变化
从图3可知,恒速度边界条件下,移动边界处的剪切应力随时间逐渐减小,并最终趋于稳定值.由于流体粘度 µ恒定,(0,t)可以直接反映移动边界处的剪切应力变化,本文认为当下平板内壁剪切速率(0,t)与稳态剪切速率(0,∞)相对差值为0.01时,Couette流动充分发展[17],即
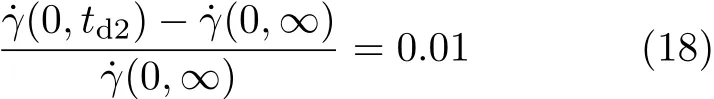
式中,td2为恒定速度边界条件下Couette流动达到充分发展的时刻.根据式 (16)与式 (18),可以计算出td2=0.537t∗时相应的非稳态过程中平板移动的距离,表示为
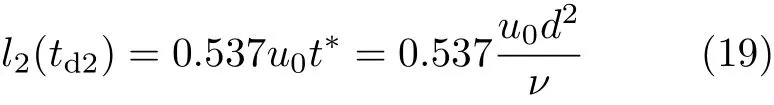
可以看出:与l1(td1)一致,在恒定速度边界条件下,非稳态阶段的平板位移l2(t=td2)同样由平板间距d、流体运动粘度ν与稳定流动时平板速度u0决定.
2.3 不同边界条件下的平板位移对比
根据式(12)、式(19),可得

所以,相同稳定流动状态的 Couette流动,控制恒定剪切应力条件下非稳态阶段边界位移l1(td1)要明显大于恒定速度边界条件下的非稳态阶段边界位移l2(td2).l1(td1)大约是l2(td2)的2.71倍.
3 流体黏性流动能量耗散
非稳态过程中,下平板对流体介质做功,一方面增加流体的动能,另一方面转换为流体黏性摩擦产生的热能.两种边界条件具有相同的稳态流动,流体速度分布相同,动能增加量也一致,所以本文将对比两种边界条件下非稳态过程中流体黏性摩擦能耗的差别.
3.1 动能增量的计算
Couette流动充分稳定后,流体速度分布满足
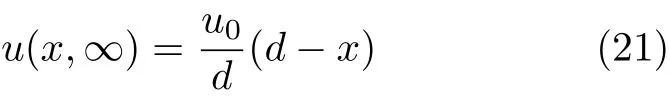
理想的Couette流动平板面积认为无穷大,单位平板面积上,稳定流动时流体动能可以描述为
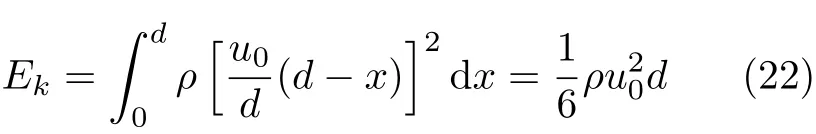
3.2 恒定剪切应力条件下的能量耗散
单位面积上,下平板拖动力在位移上的积分即为功,可以表达为
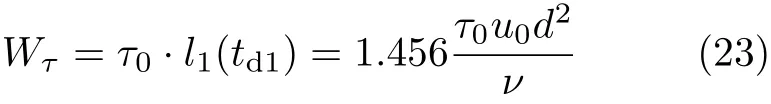
结合式(1),式(23)可以转换为
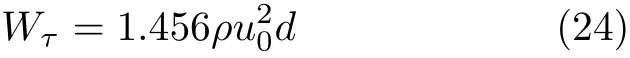
式中,Wτ为恒定剪切应力条件下,非稳态过程中,单位面积平板施加总功,ρ为流体密度.减掉动能增加量,即为摩擦能耗
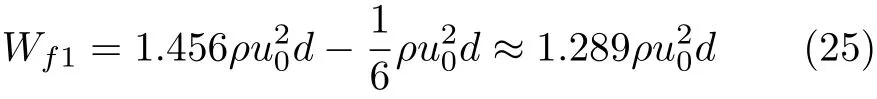
式中,Wf1为恒定应力边界条件下,非稳态过程中,单位平板面积上的流体黏性摩擦能耗.可以看出:控制恒定剪切应力边界时,单位平板面积上,非稳态Couette流动过程中,流体黏性摩擦能耗与流体密度ρ,Couette平板间距d以及稳态平板速度u0相关,而与流体黏度无关.
3.3 恒定速度边界条件下的能量耗散
恒定速度边界条件下,非稳态过程中,下平板壁面剪切应力随时间不断变化,非稳态过程中平板做功总量为拖动力在位移上的积分.根据式 (16),可以获得下平板壁面剪切应力为
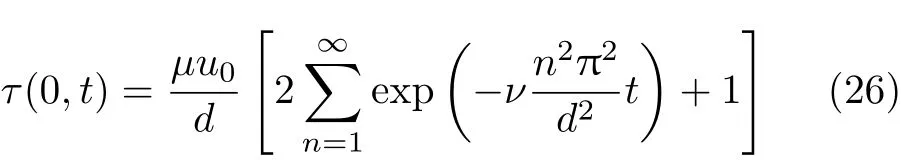
非稳态过程中,单位面积的下平板做功为
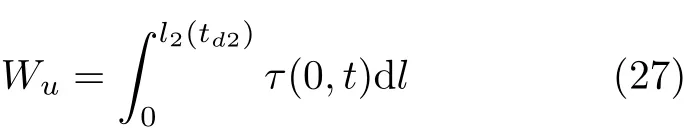
式中,Wu为恒定边界速度条件下,非稳态过程中,单位面积平板施加总功.由于边界速度恒定,所以

结合式(26)~式(28)可得
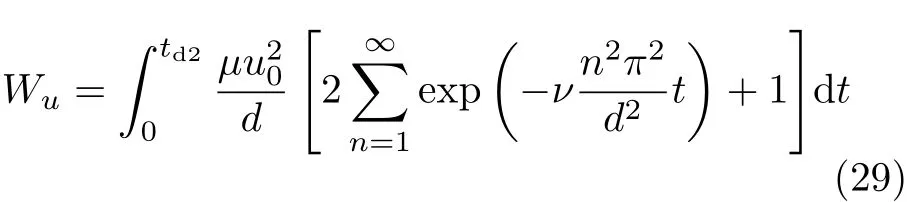
转换为
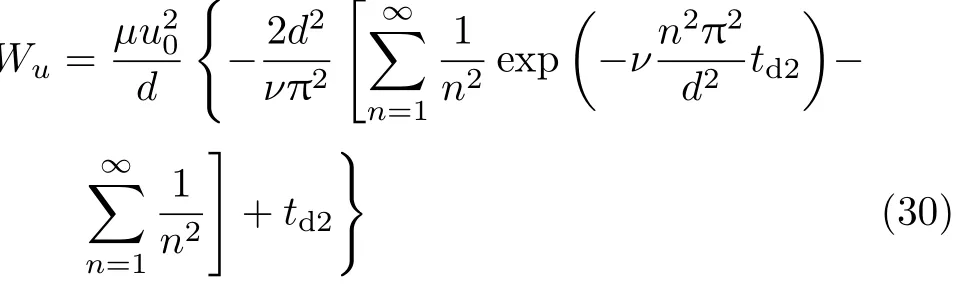
根据上文可知,td2=0.537d2/ν,所以可以求出式(30)为
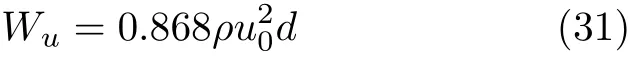
相应的非稳态过程中,单位平板面积上的流体黏性摩擦能耗为
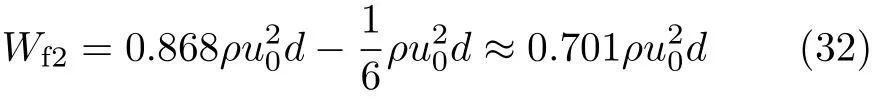
与恒定剪切应力情况一致:恒定速度边界条件下,单位平板面积上,非稳态Couette流动过程中,流体黏性摩擦能耗与流体密度ρ,Couette平板间距d以及稳态平板速度u0相关,与流体黏度无关.
3.4 不同边界条件下非稳态阶段的流体黏性摩擦能耗
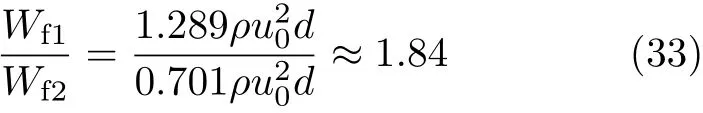
根据式(25)与式(32),不同边界条件下,非稳态过程中,单位平板面积的流体黏性摩擦能耗比值为可以看出,对于相同稳定流动状态的Couette流动,控制恒定剪切应力条件下非稳态阶段流体黏性摩擦能耗Wf1明显大于恒定速度边界条件下的非稳态阶段流体黏性摩擦能耗Wf2.Wf1大约是Wf2的1.84倍.
4 结论
(1)对于边界速度为u0的Couette稳态流动,无论采用恒定速度边界还是恒定剪切应力边界,非稳态过程中的边界位移 l均由平板间距 d、流体运动黏度ν与稳定流动时平板速度u0决定.恒定剪切应力边界条件下,非稳态过程边界位移l1(td1)显著大于恒定速度边界条件下的非稳态过程边界位移l2(td2),且前者大约是后者的2.71倍.
(2)对于同一稳态 Couette流动,无论采用恒定速度边界还是恒定剪切应力边界,非稳态流动阶段,单位平板面积上的流体黏性摩擦能耗都仅与流体密度 ρ、Couette平板间距 d以及稳态平板速度u0相关,而与流体黏度无关.恒定剪切应力边界条件下,单位平板面积上的流体黏性摩擦能耗Wf1大于恒定速度边界条件下单位平板面积上的流体黏性摩擦能耗Wf2,且Wf1大约是Wf2的1.84倍.
1 White FM,Corf i eld I.Viscous Fluid Flow.New York: McGraw-Hill,2006
2 Erdogan ME.On the f l ows produced by sudden application of a constant pressure gradient or by impulsive motion of a boundary.International Journal of Non-Linear Mechanics,2003,38(5):781-797
3 Mendiburu AA,Carroccib LR,Carvalho JA.Analytical solution for transient one-dimensional Couette f l ow considering constant and time-dependent pressure gradients. Engenharia T´ermica(Thermal Engineering),2009,8(2): 92-98
4 Shaowei W,Mingyu X.Exact solution on unsteady Couette fl ow of generalized Maxwell fl uid with fractional derivative. Acta Mechanica,2006,187(1-4):103-112
5 Bose D,Basu U.Unsteady incompressible f l ow of a generalised Oldroyed-B f l uid between two inf i nite parallel plates. World Journal of Mechanics,2013,3(2):146-151
6 Asghar S,Ahmad A.Unsteady Couette f l ow of viscous f l uid under a non-uniform magnetic f i eld.Applied Mathematics Letters,2012,25(11):1953-19587 Jha BK,Apere CA.Time-dependent MHD Couette f l ow in a porous annulus.Communications in Nonlinear Science and Numerical Simulation,2013,18(8):1959-1969
8 Ting TW.Certain non-steady f l ows of second-order f l uids. Archive for Rational Mechanics and Analysis,1963,14(1): 1-26
9 Bernardin D,Nouar C.Transient Couette f l ows of Oldroyd’s f l uids under imposed torques.Journal of Non-Newtonian Fluid Mechanics,1998,77(3):201-231
10 Muzychka YS,Yovanovich MM.Unsteady viscous f l ows and Stokes’s f i rst problem.International Journal of Thermal Sciences,2010,49(5):820-828
11 Erdogan ME.On the unsteady unidirectional f l ows generated by impulsive motion of a boundary or sudden application of a pressure gradient.International Journal of Non-Linear Mechanics,2002,37(6):1091-1106
12兰浩,张国忠,刘刚等.恒剪速下胶凝原油初始结构破坏过程力学特性.中国石油大学学报(自然科学版),2009,(2):117-121
13 Teng H,Zhang J.Modeling the thixotropic behavior of waxy crude.Industrial&Engineering Chemistry Research, 2013,52(23):8079-8089
14 Teng H,Zhang J.A new thixotropic model for waxy crude. Rheologica Acta,2013,52(10-12):903-911
15王志方,张国忠,刘刚.胶凝原油的黏弹性流变模型.高校化学工程学报,2008,22(2):351-355
16李传宪,林名桢,杨飞等.胶凝含蜡原油非线性蠕变模型研究.高校化学工程学报,2011,25(4):579-583
17 Chen L,Liu G,Zhang GZ,et al.Transient stage comparison of Couette f l ow under step shear stress and step velocity boundary conditions.International Communications in Heat and Mass Transfer,2016,75:232-239
(责任编辑:刘希国)
BOUNDARY DISPLACEMENT AND ENERGY DISSIPATION IN UNSTEADY COUETTE FLOW STAGE
YAN Yan1)
(SINOPEC Planning and Development Department,Beijing 100728,China)
The boundary displacement in the unsteady Couette f l ow stage of Newtonian f l uid is investigated in this paper.The top wall is always kept stationary and a constant velocity or a sudden constant tangential surface force is imposed on the bottom wall.The f l uid velocity distributions are obtained by solving the problems.The time periods for the f l ow to reach the steady state under dif f erent situations are obtained by using the asymptotic analytic method.Then the boundary displacements in the unsteady stage are obtained from the time periods and the boundary velocities.With the shear stress on the inner surface of the bottom wall and the boundary displacements,the work done by the Couette system under dif f erent situations is obtained.From the increase of the f l uid kinetic energy,the energy dissipations caused by the viscous friction in the unsteady Couette stage are obtained.
boundary displacement,energy dissipation,unsteady state,couette f l ow
TE81
:Adoi:10.6052/1000-0879-16-393
2016–12–05收到第1稿,2017–04–24收到修改稿.
1)闫彦,高级工程师.E-mail:dayanxiaoli@163.com
闫彦.非稳态Couette流动阶段的边界位移与黏性能量耗散.力学与实践,2017,39(4):354-358
Yan Yan.Boundary displacement and energy dissipation in unsteady Couette f l ow stage.Mechanics in Engineering, 2017,39(4):354-358

