基于CT技术的图像边缘检测及OpenCV实现*
刘洲洲,闫 伟
(1.西安航空学院电子工程学院,西安 陕西710077,2.延安大学附属医院东关放射科,延安 陕西716000)
基于CT技术的图像边缘检测及OpenCV实现*
刘洲洲1,闫 伟2
(1.西安航空学院电子工程学院,西安 陕西710077,2.延安大学附属医院东关放射科,延安 陕西716000)
计算机断层技术(CT)的出现,是人类医学史上的一大突破,标志着现代医学正式跨入数字化时代。CT图像的三维重建是医学影像学中的一个重要领域,同时口腔CT又是使用率最高的领域之一。作为图像分割的一种方法,利用开源计算机视觉库(OpenCV)具有多平台支持,多语言接口,强移植性,快处理速度等优点,使用不同的边缘提取算子提取CT图像的轮廓并进行比较,通过CT机扫描而得的图像进行双边滤波器平滑滤波,边缘保留,Canny算子边缘提取等图像预处理。在算法实现上提出了方便调试的轨迹条,可以很好地对各种参数进行可视的实时调节,便于找出最优方案。
CT技术;数字图像处理;边缘检测;开源计算机视觉库;平滑滤波;边缘提取
1 引言
图像分割作为图像分析、理解的基础,在诸多领域具有广泛的应用,如基于内容的图像检索、机器视觉、指纹识别以及生物医学图像处理方面的病变检测、军事图像处理方面的地形匹配和目标锁定[1-2]。边缘检测是基于边界识别的一类图像分割方法。边缘检测的基本思路是通过寻找图像中不同部分的边界,从而达到突出边缘。边缘是指像素灰度有阶跃性变化的区域,在图像中最直观的边界就是颜色突变的地方。边缘是图像的重要信息,是图像分割的一个重要特征。对人来说,图像的边缘部分是首先映入脑海的,可以区分物体与物体之间的界限,边缘是一个区域的结束,又是另一个区域的开端,利用边缘的特性就可以对图像进行有效的分割[3]。
2 边缘检测
计算机处理得出的边缘并不一定就是图像的真正边缘,只是在图像信息方面引起计算机注意的部分,具体参数要结合具体情况进行适当的整改[4]。由于实际物体的信息是三维的,而得到的图像数据是二维,从三维降到二维的投影必然会造成信息的缺失,再加上环境和噪声对图像采集带来的影响,使得很多边缘不能被有效的识别,识别出的边缘也不一定为真边缘。方向和幅度是边缘的两个重要属性,沿着边缘方向的像素变化比较小,较为平缓,垂直于边缘方向的像素变化较大,边缘上的这种信息变化可以用微分算子检测出来,通常使用一阶或者两阶导数来进行边缘检测。边缘大致可分成两种:一种是阶跃状的如图 1、3、5;另一种是屋顶状的如图 2、4、6。

边缘检测首先要对图像进行滤波,因为边缘检测的算法主要是对图像信息进行一阶导数或者二阶导数,但是导数对噪声很敏感,如果图像中有噪点,那边缘检测会放大这种噪声效果,通常显示为发光亮点。因此必须采用滤波器来模糊噪声带来的影响。然后是对图像进行增强,增强算法可以将邻域内比较明显的灰度变化较为明显地表现出来。经过增强的图像在邻域中可能会有一些点的幅度值比较大,但是在大部分情况下,这些幅度值较大的点并不是所需要的边缘,在编程实现中往往通过阈值法来进行选择性取舍。
3 Canny算子
在实际边缘提取的应用中,对噪声的抑制和对边缘的提取是很难同时完全满足的[5],例如高精度零件和CT等对细节边缘有着极高的要求的实例在普通边缘检测步骤下较难实现。因此选择适当的边缘检测算子、步骤和参数可以使得到的结果接近所需要的边缘提取目的。
有一个线性的算子可以在边缘检测和抗噪声中取得一个平衡,能很好地在提取边缘的同时保留一些细节,这个算子就是Gaussian函数的一阶导数。而Canny边缘检测算子就是由Gaussian函数的一阶导数构成的。JohnCanny在1986年提出Canny算子,它与使用局域窗口梯度的Sobel和Laplace算子不同,对噪声的敏感度不强,是先对图像进行平滑然后求导数的,Gaussian函数与图像的卷积可以达到抗噪的目的,导数又可以对边缘进行检测。所以Canny算子在实际进行图像处理的时候效果比较好,是最常用的边缘检测手段之一。由于Gaussian函数是一个对称函数,图像的边缘在边缘方向是对称的,在垂直于边缘的方向上是反对称的,所以Canny算子对边缘两侧的变化特别敏感,而对平行于边缘方向的变化不敏感。
设二维Gaussian函数:
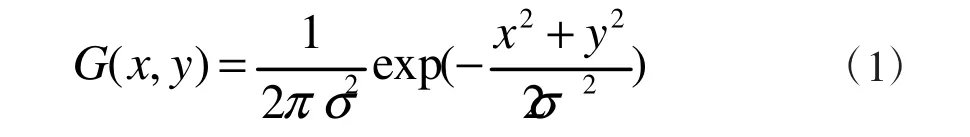
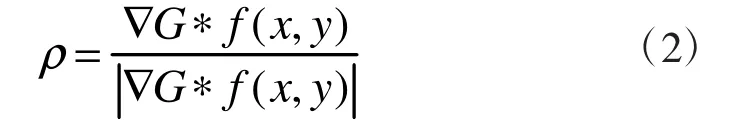
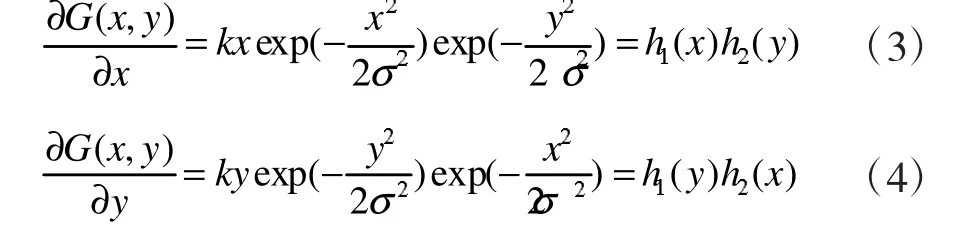
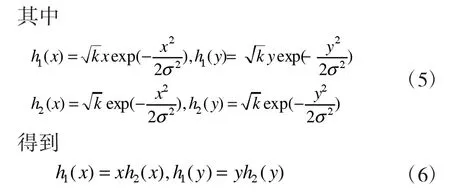
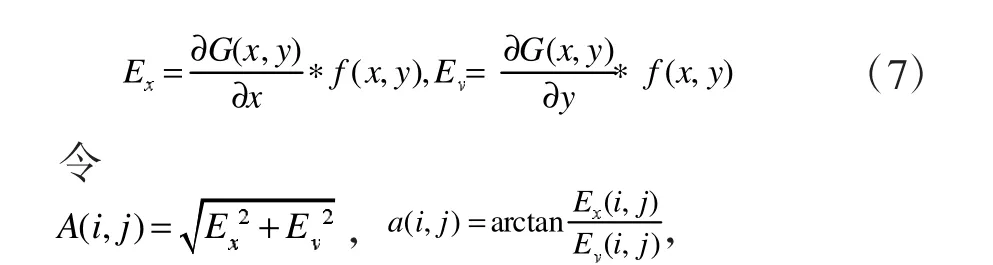
4 边缘提取的评价
Canny给出了三个评价边缘检测性能的指标[6-7]:一是低失误概率,尽量多的包含真实边缘,减少将不是边缘的部分归为边缘的错误结果;二是高精确度,得出的检测结果应该都在正确的实际边界上;三是单像素宽,对边缘有一个唯一的响应,在模糊边界中找出最优边界。针对以上三个指标,John Canny提出了用于一阶微分滤波器的边缘检测评价准则:信噪比准则:
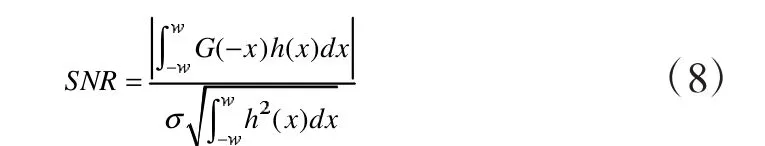
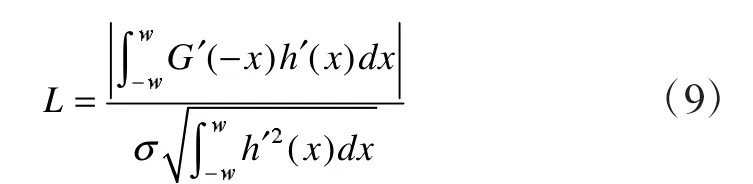
单边缘响应准则:要确保对于边缘像素只有一个单独的响应,算子的脉冲响应导数的零交叉点平均距离应满足:
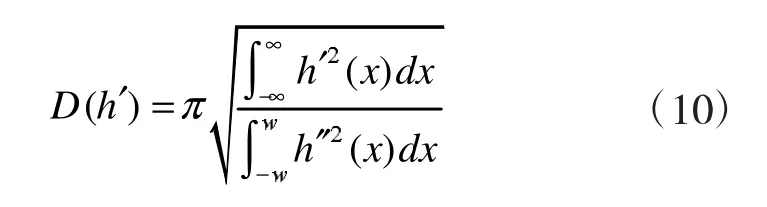
5 OpenCV实现
开源计算机视觉库(Open Source Computer Vision Library,OpenCV)[8]是因特尔公司在2000年推出的一个软件库,包含了许多针对图像处理方面的库函数,可以直接调用。OpenCV具有多平台支持,多语言接口,强移植性,快处理速度等优点。所使用的是CPU为Intel core i5-2450M的64位PC机,IDE 为 visual studio 2015,OpenCV3.0。
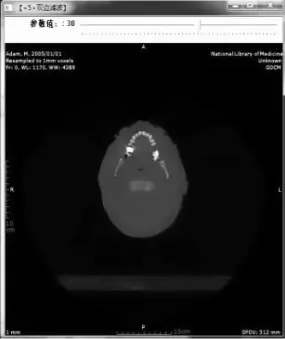
图7 经双边滤波后的原图像
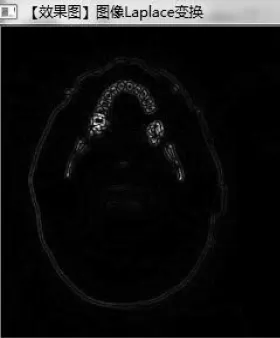
图8 Laplace算子边缘检测
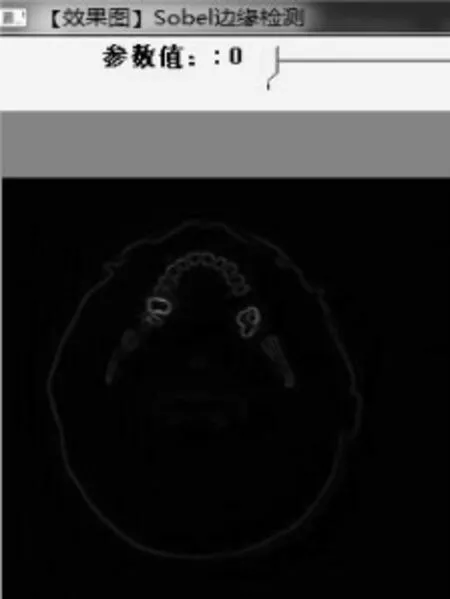
图9(a)Sobel算子参数 0
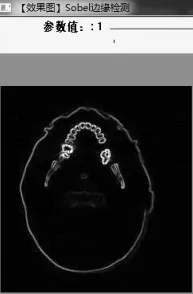
图9(b)Sobel算子参数 1
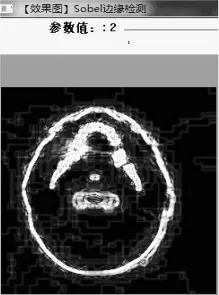
图9(c)Sobel算子参数 2
经边缘滤波平滑后的图像如图7所示,图8表示了Laplace算子边缘提取图像,图9表示Sobel算子边缘检测图像。
比较图 9(a)、图 9(b)、图 9(c)参数为 0 的时候Soble算子细节较为清楚,但是存在图像边缘不清等特点,参数为1时边缘比较清晰,但是细节处存在部分粘连,都不适合进行重建。图10表示使用Canny算子进行边缘提取。

图10(a)canny算子牙齿图像

图10(b) Canny算子保留颌骨
使用Canny算子对图像进行边缘检测对于细节的体现比较其他方法更高,参数的可调性也更优秀。图10(a)显示在参数为70时图像可以只保留牙齿图像,图10(b)则可以在参数44时保留颌骨部分的图像。Canny算子可以在实际应用中根据需要调节参数达到控制边缘部分的功能。
6 结束语
对数字图像处理及其OpenCV实现进行了学习,在了解CT成像技术的原理进行深入了解之后针对热门的口腔CT图像进行系统的整理优化,将CT机扫描而得的图像进行Canny算子边缘提取等图像预处理。在算法实现上提出了方便调试的轨迹条,可以很好地对各种参数进行可视的实时调节,便于找出最优方案。为口齿排列图像的重建工作做了较为完善的准备工作。
[1]姜赟.基于面绘制的图像三维可视化算法研究[D].成都:电子科技大学,2007.Jiang Yun.Surface Rendering the Image Based on Three-dimensional Visualization Algorithm [D].Chengdu:University of Electronic Science and technology,2007
[2]王群.CT断层图像三维重建中插值技术研究与应用[D].苏州大学,2007.Wang Qun.Study and Application of Interpolation Technique in 3D Reconstruction of CT Fault Images[D].Suzhou:Suzhou University,2007
[3]林卉,赵长胜,舒宁.基于Canny算子的边缘检测及评价[J].黑龙江工程学院学报,2003,(02):6-16.Lin Hui,Zhao Changsheng,Shu Ning.Detection and Evaluation of Canny Operator Based on[J].Journal of Heilongjiang Academy of Engineering,2003,(02):6-16.
[4]余洪山,王耀南.一种改进型Canny边缘检测算法[J].计算机工程与应用,2004,20:27-29.Yu Hongshan,Wang Yaonan.An Improved Canny Edge Detection Algorithm [J].Computer Engineering and Applications,2004,(20):27-29.
[5]曹璐,戴青云,潘晴.一种改进型Canny联合阈值分割的图像背景去除在外观专利图像检索中的应用[J].计算机工程与应用,2012,(01):208-211 Cao Lu,Dai Qingyun,Pan Qing.The Background Image of a Modified Canny Combined with Threshold Segmentation in the Removal of Design Patent Image Retrieval Using[J].Computer Engineering and Applications,2012,(01):208-211
[6]刘荣科,张晓林,廖小涛,聂振钢.基于可逆提升小波变换和上下文预测的SAR图像无损压缩算法 [J].航空学报,2002,(06):534-537.Liu Rongke,Zhang Xiaolin,Liao Xiaotao,Nie Zhengang.Lossless Compression Algorithm of SAR Image Based on Wavelet Transform and Reversible Context Prediction[J].Aircraft 2002,(06):534-537.
[7]袁勇.一种改进的中值滤波方法 [J].成都理工大学学报(自然科学版),2013,v.40;No.17702:125-129.Yuan Yong.An improved Median Filtering Method[J].Journal of Chengdu University of Technology(NATURAL SCIENCE EDITION),2013,v.40;No.17702:125-129.
[8]陈学奇.图像测量中的算法研究 [D].长沙:中南大学,2013.Chen Xueqi.Algorithm Research in Image Measurement[D].Changsha:Central South University,2013.
Image Edge Detection and OpenCV Implementation Based on CT Technology
Liu Zhouzhou1,Yan Wei2
(1.School of Electronic Engineering,Xi’an Aeronautical University,Xi’an 710077,China,2.Yan’an University Affiliated Hospital Radiology,Yan’an 716000,China)
The advent of computed tomography technique(CT)is a breakthrough of human medical history,marking the modern medicine officially entered the digital age.CT image 3D reconstruction is an important field of Medical Imageology,and oral CT is one of the fields having highest utilization rate.As a method of image segmentation,using OpenCV has some advantages such as multiple platform supporting,multilingual interface,strong portability,and quick processing.Using different edge detection operators to extract the outline of CT image and compare,the image preprocessing,such as tow-side filter smoothing filtering,edges preserving,and Canny operator edge extrcation,is executed to the images from CT scanning.A track bar easy to test is put florwand for algorithm implementation,which can make visible true time control to a variety of parameters to conveniently find optimal scheme.
CT technology;Digital image processing;Edge detection;OpenCV;Smoothing filter;Edge extraction
10.3969/j.issn.1002-2279.2017.04.021
A
1002-2279-(2017)04-0087-04
国家自然科学基金资助项目(61601365)
刘洲洲(1981—),男,山西省运城市人,博士生,研究方向:智能优化算法。
2016-09-26

