非开放式电润湿系统的电流体动力学仿真

庄 磊， 周 莹,*， 唐 彪， 李发宏， 李 楠， DEROOIJ Nicolaas Frans,3， 周国富,,3

(1. 华南师范大学华南先进光电子研究院， 彩色动态电子纸显示技术研究所， 广州 510006；2. 深圳市国华光电科技有限公司， 深圳 518110； 3. 深圳市国华光电研究院， 深圳 518110)

非开放式电润湿系统的电流体动力学仿真

庄 磊1， 周 莹1,2*， 唐 彪1， 李发宏1， 李 楠2， DEROOIJ Nicolaas Frans2,3， 周国富1,2,3

(1. 华南师范大学华南先进光电子研究院， 彩色动态电子纸显示技术研究所， 广州 510006；2. 深圳市国华光电科技有限公司， 深圳 518110； 3. 深圳市国华光电研究院， 深圳 518110)

针对以电润湿显示像素单元为代表的复杂非开放式油-水电润湿系统，通过仿真与实验结合的方法，对油-水两相微流体系的电流体动力学特性进行了研究. 基于COMSOL仿真环境，提出了油-水两相流相场与静电场，建立了包括油-水动力黏度、界面张力、润湿性等重要参数的二维动力学仿真模型，并研究了该微流体系的光电响应特性. 对比结果表明，通过层流两相流相场与静电场耦合方法成功模拟电润湿显示像素单元内的电流体动力学特性. 油膜破裂响应时间与导电液体的动力黏度正相关，但对像素最终的开口率大小影响较小；油膜破裂响应时间与油-水界面张力正相关，且主导了油-水界面的运动速度. 该模型对深入理解和预测非开放式电润湿系统的动力学性能、加速相关的研发进程有重要意义.

电润湿；电流体动力学；响应时间；开口率；动力黏度

电润湿技术由于其易操作、快速响应和电学可重复性等诸多优点，使其在微变焦透镜、芯片实验室、电子纸显示、微全分析系统(μ-TAS)等领域广泛应用[1-4]. 在这些应用中，电润湿显示器(EWD)由于透光率高、开关速度快等突出优点在过去10年内得到了快速发展.

电润湿显示技术通过改变超疏水绝缘层对导电液体的润湿性控制导电液体的运动，实现像素单元内的油膜开关. 一个完整的像素开关可以描述为3个阶段：在第一阶段中，当在疏水介质层底部电极和上基板电极之间施加电压时，垂直于油膜的体积力使油膜下降，使水接触疏水绝缘层. 在第二阶段，水接触疏水绝缘层后，三相接触线上电场发生畸变，油膜在电毛细作用和体积力的共同作用下向像素墙的两端运动. 此阶段像素单元的开口率增加，导电液体与疏水绝缘层的接触角减小，最终电润湿系统的电场能和油膜的表面势能平衡. 在第三阶段中，当电压关闭时，系统的电场能消失，油膜聚集的表面势能使油膜自由铺张，疏水绝缘层再次被油膜覆盖，像素单元关闭. 然而在现实情况下，像素的开启和关闭的过程中可能会出现翻墙、油膜不能恢复等影响光学性能的现象. 这些缺陷的出现将大大影响电润湿显示器的性能[5-6].

为了进一步提高器件的可靠性和光学性能，有必要充分了解像素单元开、关状态下流体的动态行为. 相对于实验获得数据需要消耗大量的资源而言，数值模型的参数可调性、低成本、可实时观测等优点，在指导研发生产以及理解电润湿原理起到重要作用. TANG等[7]通过薄膜润滑理论建立了封闭系统下的电润湿器件的破裂模式理论，完整地描述了油膜破裂阶段油水界面的演化过程. 然而文中应用MATLAB求解，由毛细力和界面张力引起的压力的偏微分方程，使提取接触角、油膜运动速度等参数较为困难，不利于数据可视化以及指导实际研发. CLIME等[8]通过三维Lattice-Boltzmannn模型成功实现了对电润湿数字微流控器件的传输、合并、分裂等基本操作的仿真，并与实验结果相吻合. 然而在非开放式电润湿系统中，像素墙对油膜的运动具有约束作用，Lattice-Boltzmannn模型无法体现亚毫米结构下由像素墙引起的毛细效应. HSIEH等[6]通过耦合麦克斯韦应力张量与油-水两相的相场方程的流体电动力学，完整地模拟了EWOD的施加电压油膜开启和撤去电压油膜恢复过程，并观察到了油溢、油膜不能恢复等现象. 但是油膜破裂模式以及油膜破裂后油膜的运动方向、油膜破裂的时间以及油膜恢复的时间与实验观测不符. ROGHAIR等[9]通过耦合电场高斯方程、电荷传输方程以及流体运动的Navier-Stokes方程，在OpenFOAM的框架下解决了导电体和非导电体之间的界面变形以及在外加电压影响下液-液-固三相接触线的运动以及不同阶段的油膜运动. 该方法成功解决了电润湿像素单元的开和关过程，并且和实验中的开关时间较好地吻合. 但是在仿真过程中介电质的电场常数没有梯度耦合，引起了电势分布的误差，而涉及的数值求解过程相当复杂，使得该方法的应用受到极大地限制.

近年来采用多物理场耦合，尤其是通过耦合电场与Navier-Stokes流体方程的方法，研究电润湿器件的油膜破裂、恢复等现象取得了较好的效果. COMSOL Multiphysics作为一款大型的高级仿真软件，能够便捷地实现多物理场耦合以及用户可自定义函数的优点使COMSOL在模拟多物理场耦合方面获得了广泛应用. 本文提出了在COMSOL架构下，通过耦合层流两相流相场与静电场的方法，模拟非开放式电润湿器件的油膜破裂过程，并探究导电液体的动力黏度以及油水表面张力对油膜破裂的时间、开口率的影响.

1 研究方法

1.1 测试平台

电润湿器件有明显响应时间，其响应时间在毫秒级并与施加电压相关. 为研究电润湿器件的动力学特性，本文定义电润湿器件的响应时间为从施加电压到像素单元刚有开口时间差. 为了测量电润湿器件的开口率和油膜破裂响应时间，搭建如图1所示的实验平台. 波形发生器产生频率为5 Hz的方波电压并作用于电润湿器件上，采用高速摄像机拍摄不同时间油膜破裂的图像，同时采用色度仪记录电润湿器件的反射率.

图1 电润湿显示器件开口率和响应时间的测试平台

Figure 1 Test platform for white area and response time of electrowetting display

1.2 数值方法

电润湿器件的尺寸在微米级别，此时需要考察惯性力和表面张力、重力力与表面张力、粘滞力与惯性力的关系，研究各种力在电润湿器件中的重要性. 惯性力和表面张力的关系通常用韦伯数We表征：

We=ρu(t)h2(t)/γow，

其中，ρ是液体密度，u(t)是流体运动的平均速率，h(t)为微流体的流体通道特征高度，γow为油水界面张力系数. We越小表示表面张力越重要，当We<10-5<<1时，表面张力不可忽略.

Bond数(Bo)表征系统的重力和表面张力的关系

Bo=Δρgh2(t)/γow，

其中，Δρ为油和水的密度差，g为重力加速度，γow为界面张力系数. 在电润湿器件中，Bo=1.4×10-6<<1，即重力可以忽略.

粘滞力和惯性力用于判断流体的流态. 一般来说，流体流动可分为层流和湍流. 流体做有序的成层流动且流体之间不发生相互混合，即为层流. 相反，流体做无序的随机运动且质点相互混合，这种流体流动的状态即为湍流. 流体流动属于湍流还是层流，通常依据雷诺数Re的大小进行判断

Re=Δρgh2(t)/μ,

其中，μ表示液体的动力黏度. 一般地，当Re<2 000时，为层流状态. 当流体运动速度取实验观测的最大值1 cm/s时[10]，电润湿器件的雷诺数Re=0.05<<2 000. 非开放式电润湿器件中，流体在其运动过程中各质点的黏性应力占据主导地位，惯性力可忽略，流体呈现有规则流动的层流态. 在电润湿器件中的主要作用力为体积力、表面张力以及粘滞阻力[11].

本文研究的非开放式电润湿器件同时存在水和油两种流体，计算过程中假设流体为不可压缩、互不相溶的牛顿流体，且流体在流动过程中无化学反应，则由描述粘性液体的基本力学规律的Navier-Stokes方程和质量连续方程[6,11]:

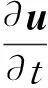
(1)

·u=0,

(2)

Fγ=γκα,

(3)

κ=-·n=-

(4)

其中, ρ、u、μ、p、γ、FE、Fγ、κ分别代表液体的密度、速度、动力黏度、压力、表面张力系数、体积力、界面张力、油水界面曲率[12]. 非开放式电润湿系统的流体流动为层流，两项流体之间无扩散效应，因此需要耦合的唯一参数是由外加电场引起的体积力FE与界面张力Fγ. 施加电场后，疏水绝缘层、像素墙、油水两相的电场强度由Laplace方程▽·(ξ0ξr▽V)=0描述，其中ξ0为真空中的介电常数，ξr为包括固体电介质和流体的相对介电常数. 而外加电场引起的流体流动体积力可以通过Korteweg-Helmholtz电功率密度公式进行计算[13]：

(5)

其中ρf自由电荷密度，油和水为介电质液体. 方程的第二项表示流体在电场作用下的极化作用对体积力的贡献. 极化作用在两相流体中只在油水界面处存在；方程的最后一项表示电致伸缩力密度，对于不可压缩流体电致伸缩力密度可忽视. 忽略电致伸缩时，体积力可以通过Maxwell应力张量的散度表示TM：

FE=·TM.

(6)

麦克斯韦应力张量可写为：

(7)

对于二维结构，麦克斯韦应力张量可以表示为：

(8)

其中，应力张量在各个方向上可以表示为

Tij=ξEiEj，

用下标i、j代表x、y方向[14].ξ、Ei和Ej代表液体的相对介电常数、电场强度在x和y方向上的分量. 在仿真中水的密度为998 g/m3，相对介电常数为80，动力黏度为1.0×10-3Pa·s，油的密度为735 g/m3，相对介电常数为2.2，动力黏度为1.2×10-3Pa·s.

对于两相流流体动，油水界面追踪是一大难题. 研究两相物质界面移动的常用方法有流体体积函数(VOF)法、水平集(Level set)法以及相场(Phase field)法. VOF方法利用物质的体积分数在网格内确定一条水平或垂直线段来描述界面. 水平集法将运动界面(两相界面)定义为φ(x,y,t)=0零等直面(线). 相场方法基于扩散界面模型，通过体系序参量和浓度场变化表征体系的界面演化. COMSOL的相场理论架构中，通过使用微分方程表示物理界面运动和化学势变化的综合作用，从而得到界面的瞬时变化. 相场法不直接追踪界面的变化，而通过相函数φ描述流体距离相界面φ=0的距离. 将相场理论应用于电润湿系统，在两项流体的区域内，相场会强制性地取±1，而在界面的过渡区域内，相场函数φ在-1～1之间平滑变化. 定义油-水界面为扩散界面，由Cahn-Hilliard对流方程描述油-水界面的变化，并通过求解相场方程得到相场变量φ. 相场法的方程描述为[15]：

(9)

φ=-φ+(φ2-1)φ+·,

(10)

(11)

其中，ζpf为界面厚度，通常取流体区域内划分最大网格尺寸的一半；χ为界面移动速率，通常取流体运动的最大速度，为混合能量密度. 油-水两相的物理化学属性不同，需要考虑密度ρ，动力黏度μ，相对介电常数ξ的差异等因素的影响. 随着油膜的运动，像素单元内电场的分布也发生改变. 由相场理论有，油-水两相的介电常数εr，密度ρ，动力黏度μ可表示为[16]：

(12)

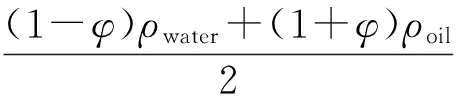
(13)

(14)

1.3 边界条件

Laplace方程求解电场除电极区外，所有的外边界均采用零电荷条件n·D=0，其中上基板接地，疏水绝缘层底部的电压为Vapp. 固体表面(如疏水性绝缘层表面、像素墙、水与顶部基板)的边界条件设置为润湿壁，固体表面接触角定义为与水的接触角θ，并由

(15)

描述[6，14]. 电润湿器件中油膜会因为油膜翻墙、油膜不能恢复等光学缺陷影响电润湿器件的功能，因此为限制油膜翻墙，像素墙采用SU-8弱疏油，可将像素墙上方对油的接触角设为125°，水与顶部基板的接触角设为90°. 实验表明，油膜处以欠填充状态，油膜将在油水界面张力以及毛细力的作用下铺展为凹液面，而像素墙弱疏油，可将像素墙侧面对油的接触角设为80°. 实验中油膜填充后疏水绝缘层与水的接触角为175°. 而介电层施加电压后疏水绝缘层的润湿性将发生变化，疏水绝缘层变为亲水性，导电液体与疏水绝缘层的接触角变小，油膜运动到像素墙两个角落，三相接触线上的电场力与油膜表面势能达到平衡，疏水绝缘层与水的接触角θV由Lipmann-Young方程描述[14,17]：

(16)

θV和θ0分别表示导电液体与疏水绝缘层在有外加电压和无外加电压下的润湿角，γow为油水界面的界面张力系数，ξ0和ξd分别表示真空的介电常数和疏水绝缘层的介电常数，实验测得油水界面的表面张力为0.022 0N/m. 导电液体的侧面壁附近液体流动可以忽略不计，设为无滑移u=0的边界条件[18-19]. 在仿真中设置上极板与导电液体侧面壁接触的其中一点的压力为0 Pa，设置为计算压力的参考点. 各物质在仿真中的几何尺寸如表1所示.

表1 各组成部分在仿真中的几何尺寸

2 结果与讨论

2.1 响应时间与开口率

当施加电压较高时，油膜一般从像素单元中间破裂，运动至像素墙的角落. 当外加电压为35 V时，将油膜破裂后的图像用Matlab进行二值化处理(图2). 油膜的运动具有空间对称性，并在打开位置有少量残油. 因此为了减少计算量，可建立垂直与疏水绝缘层的单个电润湿器件的中性截面的二维模型，研究施加电压后油膜的运动以及表面张力、动力黏度的影响.

图2 MATLAB二值化处理后的油膜破裂图像

Figure 2 Image of oil film rupture after MATLAB binaryzation treatment

实验表明油膜处于欠填充状态，油-水界面为凹液面，仿真中可在施加电压前预留5～10 ms使得油-水界面在毛细力的作用下铺展为凹液面. 基于上述方法，当施加电压为30 V时，油水界面的形状随着时间的变化如图3所示. 施加电压前，油膜在毛细力和像素墙侧边润湿壁的作用下，其油水界面铺展为凹液面. 施加电压后，油膜在体积力的作用下逐渐下降，与疏水绝缘层接触，并向像素墙运动，在施加电压2.87 ms后像素单元完全打开.

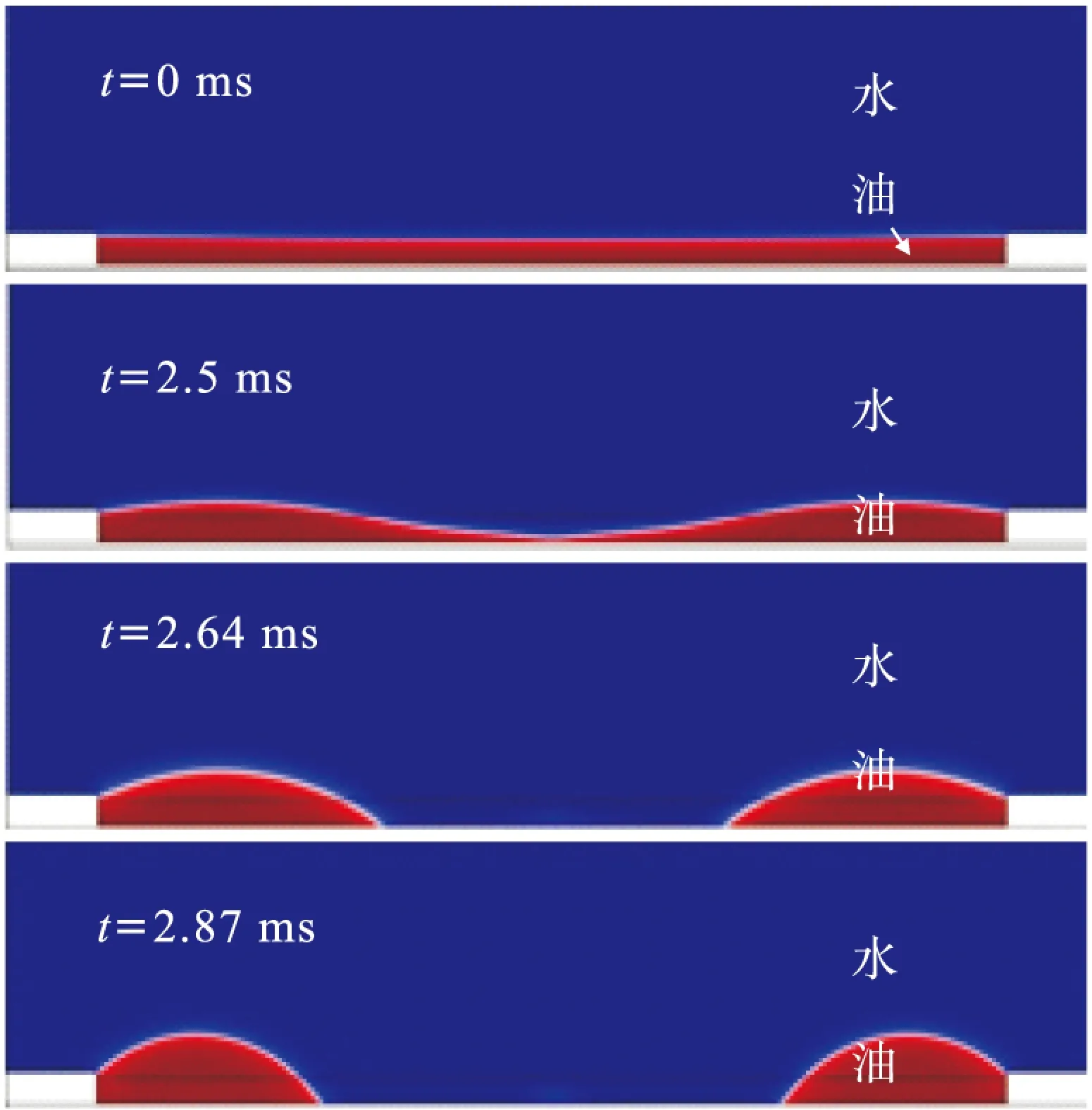
图3 30 V条件下不同时间油水分布的动力学仿真

Figure 3 Dynamics simulation of oil-water distribution changes over time under 30 V

采用实验和仿真研究不同电压下油膜破裂的响应时间、像素开口率的变化规律. 随着电压的增加，油膜破裂的响应时间逐渐缩短，且实验和仿真的结果变化趋势一致(图4A)；不同电压下像素开口率相近，且稳态下像素开口率的实验值和仿真值的差别在2%以内(图4B)；施加不同的电压后油膜均从中间破裂，与实验观测油膜由像素单元中间位置破裂一致(图4C). 因此，通过层流两相流相场与静电场耦合方法成功模拟了电润湿显示像素单元开阶段的电流体动力学特性.

图4 不同电压下的油膜破裂响应时间、开口率以及电流体油水分布的动力学仿真

Figure 4 Film rupture time, white area and the dynamics simulation of oil-water distribution under different voltages

2.2 表面张力对开口率及油膜破裂时间的影响

文献研究[10,12,20]表明，像素墙的大小、油膜的厚度以及油水界面张力是影响电润湿的光学元件电光性能的关键参数，油水界面张力的减少强烈影响油水界面移动的速度. 采用层流两相流相场和静电场耦合的方法研究表面张力对开口率及油膜破裂时间的影响(图5)表明，当驱动电压不变、油-水表面张力降低时，油膜的开口率增加，响应时间缩短，油膜运动速度加快，光电开曲线变陡.

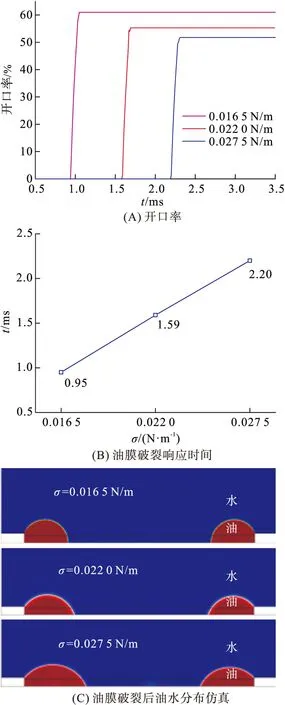
图5 不同表面张力对35 V下的开口率、油膜破裂响应时间以及油水分布的影响

Figure 5 White area, film rupture time and oil-water distribution with different surface tension under 35 V

2.3 动力黏度对开口率及油膜破裂时间的影响

雷诺数的计算结果表明，粘滞阻力是电润湿器件中的主要作用力. 恒温下，由两种互不相溶、不可压缩的粘性液体引起的粘滞阻力消耗着外加场的能量，将对油膜的打开时间、油膜完全破裂的时间以及油膜能否完全恢复有影响. 采用层流两相流相场和静电场耦合方法，研究导电液体动力黏度对开口率以及油膜破裂时间的影响(图6)，随着导电液体动力黏度的增大，层流间的粘滞阻力消耗外加场的能量增加，油膜的运动速度变慢，油膜破裂的响应时间以及油膜完全破裂的时间延长.

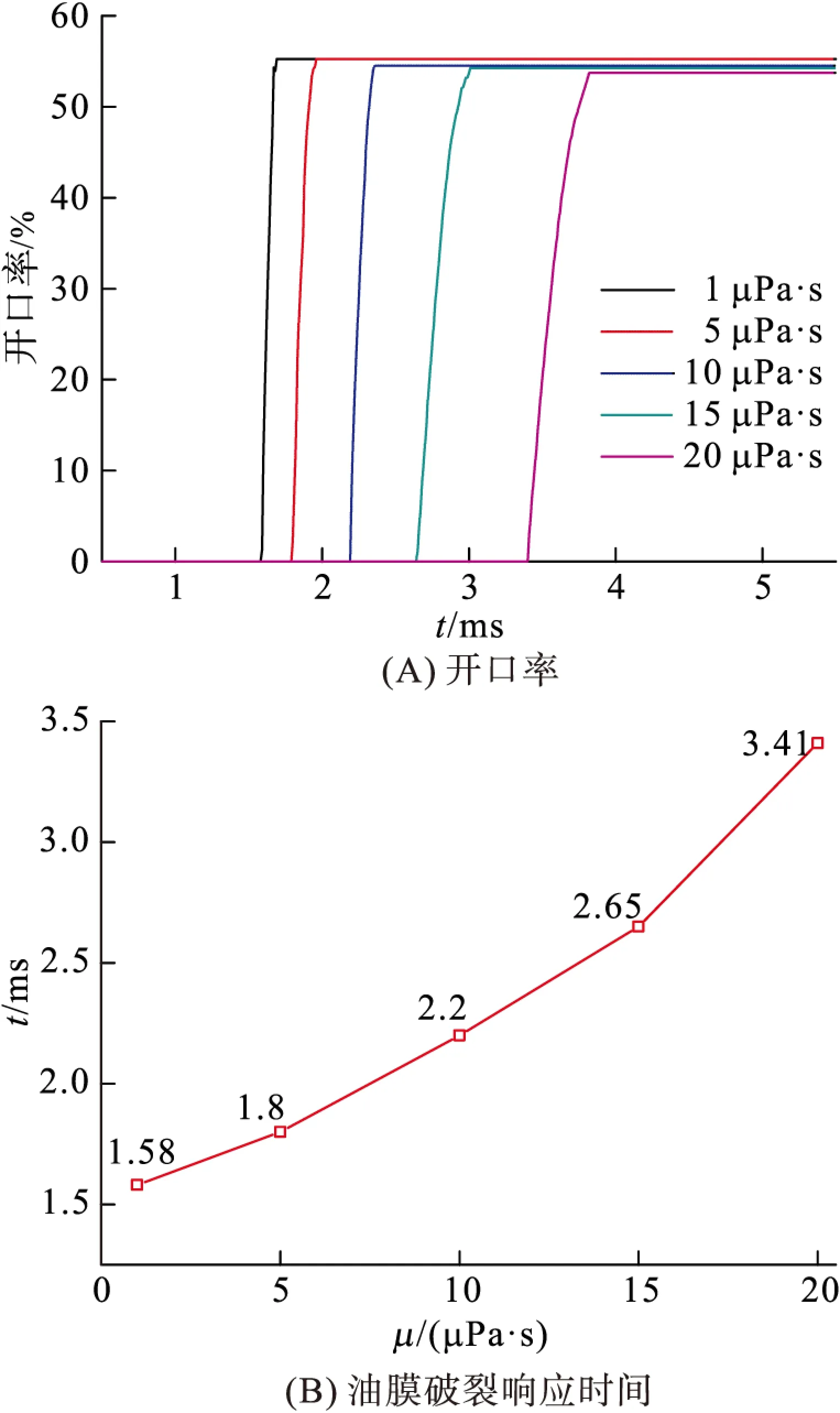
图6 不同动力黏度的导电液体在35 V条件下的开口率及油膜破裂响应时间

Figure 6 White area and oil film rupture time of conductive liquid with different dynamics viscosity under 35 V

3 结论

本文通过耦合层流两相流相场与静电场方法，模拟非开放式电润湿器件的油膜破裂的二维动力学模型. 通过对比实验和仿真结果，不同电压下油膜破裂响应时间以及油膜的开口率随时间的变化，验证了该方法的有效性. 外加电压为35 V时，油膜破裂的响应时间的实验值与仿真值相差较大，可能是由仿真中的数值耗散、仿真的二维模型与实验的三维结构的差异引起的. 进一步验证改模型的可靠性可以进行层流两相流相场与静电场三维仿真.

对表面张力的研究结果表明，当油水界面张力由0.016 5 N/m增加到0.027 5 N/m时，油膜破裂的响应时间由0.95 ms变为2.2 ms，即油膜破裂响应时间与界面张力成正相关，且强烈影响着油水界面的引动速度. 对导电液体动力黏度的研究结果表明，导电液体的动力黏度由1 μPa·s增加到20 μPa·s时，油膜完全破裂响应时间由1.58 ms延长到3.41 ms，而开口率由55.26%减小到53.72%，油膜破裂的响应时间与导电液体的动力黏度正相关，但对像素最终的开口率大小影响较小.

本研究表明，层流两相流相场与静电场的耦合成功地模拟了电润湿器件的开阶段动力学特性，这对预测不同导电液体材料的光学特性成为可能，对电润湿器件的研发具有一定的理论指导意义.

[1] KANG M,YUE R. Variable-Focus liquid lens based on EWOD[J]. Journal of Adhesion Science & Technology,2012,26(12-17):1941-1946.

[2] CHO S K,MOON H,KIM C J,et al. Creating,transporting,cutting,and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits[J]. Journal of Microelectromechanical Systems,2003,12(1):70-80.

[3] YOU H,STECKL A J. Electrowetting on flexible substrates[J]. Journal of Adhesion Science & Technology,2012,26(12-17):1931-1939.

[4] ZHOU J,YANG S,ZENG X Y,et al. Superhydrophobic ZnO for EWOD digital microfluidic device for application in micro total analysis system (μ-TAS)[J]. Journal of Adhesion Science & Technology,2012,26(12-17):2087-2098.

[5] HAYES R,FEENSTRA B J. Video-speed electronic paper based on electrowetting[J]. Nature,2003,425(6956): 383-385.

[6] HSIEH W L,LIN C H,LO K L,et al. 3D electrohydrodynamic simulation of electrowetting displays[J]. Journal of Micromechanics & Microengineering,2014,24(12):125024.

[7] TANG B,GROENEWOLD J,ZHOU M,et al. Interfacial electrofluidics in confined systems[J]. Scientific Reports,2016,6:26593.

[8] CLIME L,BRASSARD D,VERES T. Numerical modeling of electrowetting transport processes for digital microflui-dics[J]. Microfluidics & Nanofluidics,2010,8(5):599-608.

[9] ROGHAIR I,MUSTERD M,ENDE D V D,et al. A numerical technique to simulate display pixels based on electrowetting[J]. Microfluidics & Nanofluidics,2015,19(2):465-482.

[10]ROQUES-CARMES T,PALMIER S,HAYES R A,et al.The effect of the oil/water interfacial tension on electrowetting driven fluid motion[J]. Colloids & Surfaces A:Physicochemical & Engineering Aspects,2005,267(1/2/3):56-63.

[11]GU Y,LI D. A model for a liquid drop spreading on a so-lid surface[J]. Colloids & Surfaces A：Physicochemical & Engineering Aspects,1998,142(2/3):243-256.

[12]BRACKBILL J U,KOTHE D B,ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics,1992,100(2):335-354.

[13]LANDAU L D,LIFSHITZ E M,SYKES J B,et al. Electrodynamics of continuous media[J]. Physics Today,1961,14(10):48-50.

[14]VERMEULEN P,FEENSTRA J,GIRALDO A,et al. Mode-ling of the performance of electrowetting displays[J]. Sid Symposium Digest of Technical Papers,2011,42(1):1573-1576.

[15]STEINBACH I,PEZZOLLA F,NESTLER B,et al. A phase field concept for multiphase systems[J]. Physica D: Nonlinear Phenomena,1996,94(3):135-147.

[16]XIE Y,SUN M,JIN M,et al. Two-phase microfluidic flow modeling in an electrowetting display microwell[J]. European Physical Journal E,2016,39(2):16.

[17]ROQUES-CARMES T,HAYES R A,FEENSTRA B J,et al. Liquid behavior inside a reflective display pixel based on electrowetting[J]. Journal of Applied Physics,2004,95(8):4389-4396.

[18]ZHU Y,GRANICK S. Limits of the hydrodynamic no-slip boundary condition[J]. Physical Review Letters,2002,88(10):106102.

[19]REN W Q,TRINH P H,WEI E. On the distinguished limits of the Navier slip model of the moving contact line problem[J]. Journal of Fluid Mechanics,2014,772:107-126.

[20]ROQUES-CARMES T,HAYES R A,SCHLANGEN L J M.A physical model describing the electro-optic behavior of switchable optical elements based on electrowetting[J]. Journal of Applied Physics,2004,96(11):6267-6271.

【中文责编：谭春林 英文审校：李海航】

Electrohydrodynamic Simulation of Confined Electrowetting Display

ZHUANG Lei1， ZHOU Ying1,2*， TANG Biao1， LI Fahong1， LI Nan2， DEROOIJ Nicolaas Frans2,3， ZHOU Guofu1,2,3

(1. Institute of Electronic Paper Displays, South China Academy of Advanced Optoelectronics, South China Normal University, Guangzhou 510006, China;2. Shenzhen Guohua Optoelectronics Tech. Co. Ltd., Shenzhen 518110, China; 3. Academy of Shenzhen Guohua Optoelectronics, Shenzhen 5181101, China)

Focused on the display represented by electrowetting display pixel unit of complex confined oil-water electrowetting system, and combined the simulation and experiments, two-phase electricfluid dynamic characteristics of the microflow system were studied. Based on phase field and electrostatic field for two-phase flow offered by COMSOL, a two-dimensional dynamic simulation model including important parameters, such as, the oil-water viscosity, surface tension, wettability was built up and photoelectric characteristics of the microflow system was investigated. The results show that the dynamic characteristics of the electricfluid in the pixel cell can be simulated successfully by the coupling method of two-phase flow field and electrostatic field. The dynamic viscosity of conducting liquid is positively related to the oil film optical response time, but eventually has little effect on the white area of pixel; the oil-water surface tension value is positively related with the oil film rupture time and led the movement speed of the oil-water interface. The model makes great significance to understand and predict the dynamic performance of the confined electrowetting system and accelerate the development process.

electrowetting; electrohydrodynamics; response time; white area; dynamics viscosity

2017-03-23 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

教育部长江学者和创新团队发展计划项目(IRT13064)；国家高等学校学科创新引智计划111引智基地-光信息引智基地；国家自然科学基金委员会-荷兰国家基金机构间合作重点项目(NSFC-NWO，51561135014)；广东省引进第四批领军人才专项资金项目(Nicolaas Frans deRooij，2014年)；广东省引进第四批创新科研团队(2013C102)；广东省重大专项(2014B090914004，2016B090909001)；广东省科技计划项目(2014A030308013，2014B090914004)；广东省产学研项目(2016B090918083)；深圳融资项目(GQYCZZ20150721150406)

O411.3

A

1000-5463(2017)04-0016-07

*通讯作者:周莹, Email:zhouying@m.scnu.edu.cn.