煤矿井下分布式光纤传感系统的救援定位方法

陈丽娟， 陈立国， 张文祥

(1.黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022； 2.上汽通用北盛汽车有限公司， 沈阳 110000)

煤矿井下分布式光纤传感系统的救援定位方法

陈丽娟1， 陈立国2， 张文祥1

(1.黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022； 2.上汽通用北盛汽车有限公司， 沈阳 110000)

为了精确定位矿难发生时井下生存人员的位置，结合矿井下的特殊环境，设计了一套无源、高灵敏度、高光信噪比的井下救援监测系统。该系统以分布式全光纤振动传感系统为核心，提出双光缆共用一套干涉的系统结构,采用线性安装，对采集的传感器信号进行小波去噪处理，根据小波去噪的功率谱估计，获得陷波点的位置，计算求得扰动发生的位置，定位振动点。结果表明：该系统具有可靠稳定、定位准确等特点，适用于井下矿难发生时的紧急救援。

煤矿； 救援定位； 分布式光纤传感； 振动传感； 最大信噪比； 小波降噪

0 引 言

煤矿井下一旦发生事故，通信定位的精度直接影响到救援的效果。因此，需要建立科学的适合煤矿井下的通信定位系统。矿井下空气湿度大，空气中浮游杂质如煤尘含量高，腐蚀性气体如CO2、NO、NO2、SO2等含量较高、地理环境复杂。

光纤传感系统因为具有无源、高灵敏度、高光信噪比等特点，非常适合在矿井下应用。分布式光纤传感技术主要为以下两类，一是基于干涉原理的分布式振动传感技术[1]；二是基于后向散射探测技术的光纤传感系统。基于干涉型分布式传感技术大多采用马赫-泽德(M-Z)、萨格纳克(Sagnac)或迈克尔逊(Michelson)等干涉仪混合使用，通过等光程的光束产生干涉。上海交通大学国家重点实验室的周正仙、肖石林等，英国科学家 S． J． Spammer 等、复旦大学贾波及其团队都在做这方面的研究。课题组在研究现有大量的光纤振动传感系统的基础上，提出基于线型的Sagnac的干涉型光纤传感器矿井救援系统。在矿难发生后，只要坑道内的光缆未受物理性损坏，被困工作人员可连续敲击光缆或光缆周边的巷道壁，依据光波在光纤传输过程当中偏振、相位等参量对振动敏感的特征，使光纤中传输光的相位发生改变，从而向基站发出求救信号[2]，为了对被困人员进行高精度的定位，可将测定范围是150 km的干涉系统，定位精度控制在20 m以内，可为事故抢险提供科学依据。

1 系统构建

根据以往光纤振动传感系统大多采用环状结构，具有结构稍显复杂，环境因素对监测结果的影响较大，无法实现定位结果的唯一性，而且在矿井下这样复杂的地理环境，光纤不容易以环形安装的特点，文中提出的基于白光干涉技术的分布式全光纤振动传感系统采用线状结构。在传感光缆部分该系统只运用一根光纤便可实现对扰动信号的定位，也就是说实现对整条坑道的分布式监测实际只需在坑道内完成一根光缆的铺设即可，安装中非常便捷。传感光缆只用一根，当其中有一个断点，整个救援系统就会全部处于瘫痪状态。为了确保当矿难发生时，系统仍然处于正常工作状态。系统设置上铺设了双路光纤，并且这双路光缆共用一套光路干涉系统，克服了各用一套光纤干涉系统不利于在大范围、长距离井下定位系统中应用的缺点，具有较强的实用性和可行性。图1为系统结构示意。

图1 系统结构

系统以sagnac结构为母本，主要由超辐射发光光源(SLD)、耦合器(1,2,3)，光纤延时线圈，法拉第旋转镜(5,7)组成[3]。两路传感光纤互相独立，因此，只考虑其中一根光纤第I路发生振动产生的定位结果。依据干涉原理，在光源发出的众多光路中，只有光程相等的两束光能发生干涉。这里只考虑由SLD光源发出的红外光经耦合器1分成的两束光程相等的光路。一光束从耦合器1发出后, 经耦合器3进入延时线圈8, 后经法拉第旋转镜9反射后再经过延时线圈8, 之后沿着耦合器3, 经由耦合器2进入传感光缆,后由另一个法拉第旋转镜5反射回来, 再经耦合器2到达耦合器1,设此光路为光路A. 分析另一束光束，从耦合器1发出后进入耦合器2, 后经传感光缆传输, 在传感光缆的尾端经法拉第旋转镜5反射后, 重新进入耦合器2, 由它进入耦合器3,经过延时线圈8, 法拉第旋转镜9，再经延时线圈8，最终和前一束光汇聚在耦合器1里,称此光路为光路B. 两光束的完整传播路径如下:

A 1-3-8-9-8-3-2-4-5-4-2-1, 经过耦合器5次，经过延时线圈2次；

B 1-2-4-5-4-2-3-8-9-8-3-1. 经过耦合器5次，经过延时线圈2次。

假设振动发生在距离分光器x的位置，振动点到法拉第旋转镜的距离为L-x, 设激光两次经过此位置的时间间隔为T, 则T与L,x的关系式可表示为

式中：c——光在真空中的传播速度； n——光纤的有效折射率。

根据获得的两路干涉光强时域信号解调出这两束相干光的相位差信号；对相位差信号进行傅里叶变换，得到相位差的频谱，进行功率谱估计；找到功率谱估计中的缺失频率，即陷波频率，计算出扰动发生的位置[4]。

2 小波去噪

鉴于快速傅里叶变换的分辨率随时间是固定不变的，而小波变换则能给出可变的分辨率，采用小波变换去噪来完成系统的去噪问题。系统输入到SP的信号是有限频带中的一个信号，小波变换可以把这个信号分解成高频部分和低频部分，低频部分通常包含信号的主要信息，高频部分则与噪声及扰动联系在一起。根据分析的需要可以继续对所得到的低频部分进行分解，如此又得到了更低频部分的信号和频率相对较高部分的信号[5]。不断进行高低分层，来完成噪声信号的去除。

连续时间信号x(t)的小波变换(CWT)可以定义为

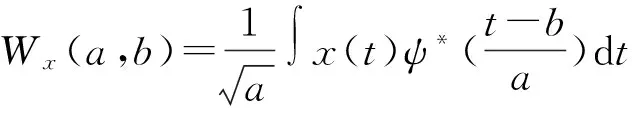
(1)

式中:b——时移； a——尺度因子。

ψ(t)称为基本小波或母小波。ψa,b(t)是母小波经移位和伸缩所产生的一族函数，ψ*(t)，是母小波的共轭函数。

鉴于CWT中各参量携带了大量的冗余信息，可将尺度参量按幂级数进行离散化处理，对时间进行均匀离散取值，可以定义离散化后的小波变换DWT为：

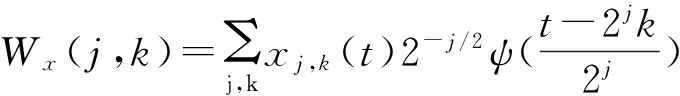
(2)

小波收缩去噪法(非线性小波变化阈值法)是基于噪声信号的小波系数门限的思想提出的，而光纤的光偏振态变化属于非线性变化，该方法非常适用于分布式白光干涉传感系统信号检测信号数据做降噪处理。去除高频分量留下低频分量。小波变换的方法去除了存在的噪声保留了信号的信息而不考虑信号的频域内容。对于分布式白光干涉传感系统小波收缩去噪法的实现方法包括以下三个步骤：第一，将信号进行DWT运算获得小波系数。第二，选择合适的小波系数门限方法。第三，根据DWT的逆变换重建去噪信号。因为掺杂在信号中的噪声通常对应在小波系数中比较小的绝对值，则通过门限的合适选取，小波系数中的噪声会被去除。

3 振动点定位方法

根据系统搭建图所示，若在光纤4或6处发生扰动，使得光束A和光束B产生相位差，

Δφ(t)=φA(t)-φB(t)={sin[w(t-τ)]+sin[w(t+τ+t0)}-{sin[wt]+sin[w(t+t0)]]，

(3)

利用三角函数式(3)可被简化为

(4)

分析可见扰动信号与相位差信号具有相同频率，扰动信号的频率和扰动发生的位置与相位差幅度相关，即

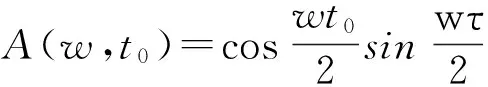
(5)

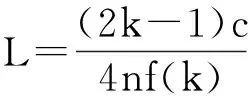
(6)

为了更精准地对振动点进行定位，可以对还原信号进行准确的功率谱分析，进行小波去噪之后查询功率谱中极小值的位置进而推算出振动点的位置。

在分析比较之后，选用WELCH功率谱估计方法：

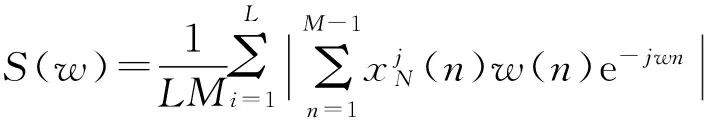
(7)

式中：M——每段信号的长度；

L——信号的分段数；

w(n)——窗函数；

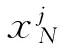
4 实验数据分析

系统搭建见图1，SP对反馈的振动信号做分析与处理。首先对被监测信号进行功率谱分析，然后对小波去噪后的功率谱分析。通过对多个层次的降噪数据进行比较分析后， 兼顾信噪比的提高程度与频率测量范围， 选择的分解层数为6。

分析可知，系统中有两种主要的噪声：一种主要是由检测器产生的散弹噪声：

Δf——接收机的带宽。

另一种是在光波传输过程中产生的热噪声：

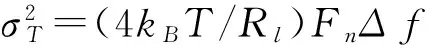
式中：kB——玻尔兹曼常量； T——绝对温度； Rl——负载电阻[5]。

这样,信噪比可表示为：

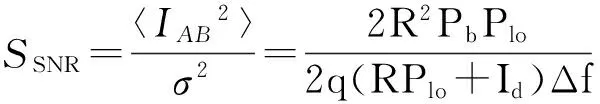
(8)

通过实验，可以找出不同脉宽和本地时钟功率下的脉冲峰值功率和信噪比之间的最优值，进而确定最佳信噪比。

在实验中，脉冲速率是50kHz,脉冲宽度分别设为30、10ns。对于不同的脉冲峰值功率获取了5 000个轨迹来计算信噪比。图2说明对于脉宽为30和10ns时不同的脉冲峰值功率估算出来的信噪比值。由图2可见，当本地时钟功率是-7.8dBm时，对于30和10ns脉宽来讲，随着脉冲峰值功率的增加SNR几乎成线性增长。可见系统的热噪声限值是由本地功率决定的。由信噪比的计算公式可见，SNR是和热噪声限值下的平均信号功率成比例的。当本地功率增长到0.2dBm系统主要受散弹噪声影响，热噪声可以忽略不计。随着脉冲峰值功率的增加SNR也跟着增加。图2显示，信噪比会增长到最高值后随着脉冲峰值功率的增加而下降，这是因为检测系统最高增益为10V/mW已经达到饱和。根据图示，对于本地晶振功率为0.2dB，脉冲宽度为30和10ns时，可以选取脉冲峰值功率为250和300dB，此时具有最佳信噪比。

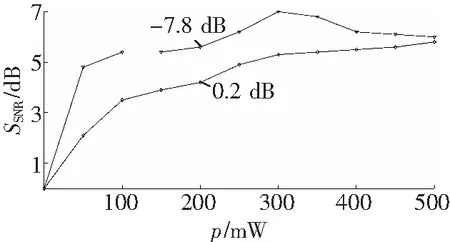
a 脉冲宽度为10 ns

b 脉冲宽度为30 ns

5 振动信号检测与定位

将0.6 m的单模光纤延迟环引入该系统，在距离分光器5 km的位置给光纤振动信号作为振动源。实验中，脉冲的带宽为10 ns,脉冲峰值功率为450 MW，可获得在本地时钟功率为0.2 dBm时最佳信噪比。时钟的晶振是500 MHz，可获得1 000条曲线。考虑到振动源的频率范围，脉冲重复率为10～5.0×104Hz。图3分别给出了振动源频率是30和10 Hz时候的振动位置信息。

可见振动源频率是30 Hz的噪声幅度比10 Hz的低，这说明在高频较高频率上噪声比较小，可获得较高的信噪比。在可以选择振源频率的情况下，可尽可能选择高频振动信号。

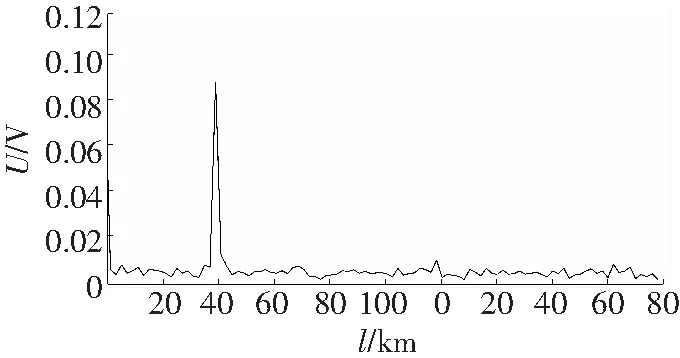
a

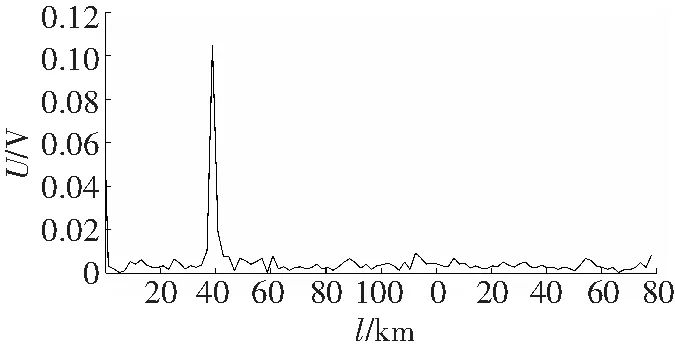
b

图4为经过小波去噪后的功率谱包络，相对没有进行小波去噪时更为平滑；图5为获得陷波点的清晰频率，获得的陷波点频率为：2 342.1、3 845.6 、5 213.5、5 968.3、6 838.7、8 168.5 Hz。

图4 功率谱包络

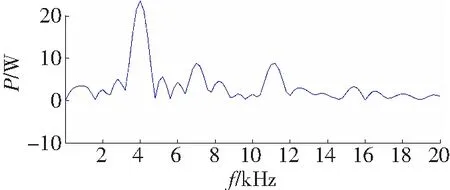
图5 功率谱陷波点

这里取光纤折射率为 1.48，根据得到的一系列陷波频率，将其代入式(6)可计算出振动点发生的位置。经计算振动点位置为8.573 km，相对真实振动点位置定位误差为18 m。

改变振动点位置，同样原理可以获得定位距离，实际振动位置x和定位距离l结果见表1所示。其中，振动点位x，数据处理前定位距离L，处理前定位误差ex，数据处理后定位距离lc，数据处理后定位误差ec。从表1可见，实际振动点和实际距离基本一致，该系统可以完成传感光纤为150 km的精确定位，经计算平均定位误差为±15 m，相对平均定位误差为0.01%，相比不进行最佳信噪比优化和小波去噪之前的平均定位误差30.5 m，定位准确率提高了0.010 3%。

表1 系统定位距离与误差

6 结束语

分布式光纤传感的矿井下救援通信定位系统有一定的实用价值。在原有的研究基础上，结合煤矿井下的特殊环境，提出改进的线状Sagnac分布式光

纤传感系统，并采用双光缆共用一套干涉系统的方法，解决了可靠性的问题。针对如何提高系统定位精度问题，采用小波去噪法，该方法使功率谱更为平滑。通过实验分析证明，监控系统可靠性更高，定位精度更准确，为矿井应急救援提供了可靠的通信支持。

[1] 孙晓东， 任晓霞， 王 琳. 应用于定位的光纤振动传感技术的发展现状[J]. 工业仪表与自动化装置， 2016(2)： 21-25.

[2] 姜曰科. 基于光纤传感技术的振动解调系统及其应用[D]． 济南: 山东大学, 2009．

[3] 皮少华, 王冰洁, 赵 栋, 等. 分布式光纤Sagnac干涉仪中基于倒谱的多分辨率入侵定位算法[J]. 物理学报， 2016(4)： 1-9.[4] 李楚瑞.基于分布式光纤振动传感技术的井下事故救援监测系统[D]. 上海： 复旦大学， 2012.

[5] Qin Zengguang, Chen Liang, Bao Xiaoyi. Wavelet denoising method for improving detection performance of istributed Vibration Sensor[J]. IEEE Photonics Technology Letters, 2012, 24, (7): 121-125.

[6] Gao L A, Liu S C, Yin Z W. Fiber-optic vibration sensor based on beat frequency and frequency-modulation demodulation techniques[J]. IEEE Photon. Technol Lett, 2011, 23,(1): 18-20. [7] 穆立波, 吴悦峰, 姚 剑. 分布式光纤震动传感系统的多点定位问题研究[J]. 传感器与微系统， 2010(9)： 21-25

[8] 周正仙， 肖石林， 仝芳轩. 基于 M - Z 干涉原理的定位式光纤振动传感器[J]. 光通信研究， 2009(5): 67-70．

[9] 谭 靖， 陈伟民， 符玉梅． 基于Sagnac原理的单轴分布式光纤传感系统偏振态分析[J]． 光子学报， 2007， 36(3)： 492-497．[10] Qin Z, Chen L, Bao X. Wavelet denoisingmethod for improving detection performance of distributed vibration sensor[J]. IEEE Photonics Technology Letter, 2012, 24(7): 542-544.

[11] Zhu T, He Q, Xiao X, et al.Modulated pulses based distributed vibration sensing with high frequency response and spatial resolution[J]. Optics Express, 2013, 21(3): 2953-2963.

[12] Tu G, Zhang X, Zhang Y, et al. The development of Φ-OTDR system for quantitative vibration measurement[J]. IEEE Photonics Technology Letter, 2015, 27(12):1349-1352.

(编辑 晁晓筠 校对 李德根)

Research on positioning method of distributed optical fiber sensor for underground rescue system

ChenLijuan1,ChenLiguo2,ZhangWenxiang

(1.School of Electronics & Information Engineering, Heilongjiang University of Science & Technology,Heilongjiang, Harbin 150022, China; 2. Shanghai GM North Automobile Co., Ltd., Liaoning 110000, China)

The accuracy of communication positioning in underground mines has a direct effect on the rescue operation. This paper, combined with the special environment in the mines, presents a passive optical fiber sensing system designed with a high sensitivity and a high optical signal-to-noise ratio. This sensing system, based on Sagnac structure uniquely constructed using linear installation, owes its improved reliability to the following steps: employing a set of optical fiber cable interference system for dual-fiber cable; given a fixed resolution of the fast Fourier transform over time, eliminating the denoising in the system using wavelet transform denoising method; and using the power spectrum estimation of wavelet denoising to secure the location of the notch point and thereby calculate the disturbance location-locating the vibration point. The experiment demonstrates that the system affords a more reliable stability and a higher positioning accuracy and could work better for the emergency rescue in mine accidents.

coal mine; rescue positioning; distributed optical fiber sensor; vibration sensor; Maximum Signal-to-noise ratio; wavelet denoising

2017-04-23

国家重大科学仪器设备开发专项项目(2012YQ150213)

陈丽娟(1981-)，女，吉林省吉林人，讲师，硕士，研究方向：矿井通信、通信网络，E-mail:chenlijuan0131@163.com。

10.3969/j.issn.2095-7262.2017.05.022

TD76

2095-7262(2017)05-0560-05

A