煤矿井下超宽带混沌键控的通信模型及性能

王 娟， 李锦峰， 那 宇

(黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022)

煤矿井下超宽带混沌键控的通信模型及性能

王 娟， 李锦峰， 那 宇

(黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022)

针对传统差分超宽带混沌键控接收延时电路难以实现低成本、低功耗的有效集成，提出将码域正交的超宽带混沌键控CS-DCSK应用于煤矿井下实现超宽带通信，仿真研究Nakagami多径衰落信道在井下巷道中的通信性能及传播特性。结果表明：CS-DCSK的误码性能与Nakagami信道的衰落指数、多径个数和扩频因子等参数有关。在信道、信噪比和扩频因子相同的情况下， CS-DCSK的通信性能优于FM-DCSK和CD-DCSK，通过合理选择参数可以使该模型的系统性能达到最优。

井下无线通信； 煤矿； 超宽带； 混沌键控

0 引 言

超宽带是利用纳秒至皮秒级的非正弦窄脉冲来传输数据，具有高速率、微功率、低功耗、低成本、抗多径、低截获以及穿墙、成像、定位等特点[1]。混沌的确定性、类随机性和初值敏感性，使其可以提供数量众多、性能优异的非周期超宽带信号[2]。将混沌信号作为载波，在完成数字调制的同时直接实现频谱扩展，能够获得更好的抗噪声干扰、抗多径衰落和抗参数敏感的能力[3]。由于基本不存在对其它窄带通信的干扰问题，使其可以不受地面应用时FCC对发射功率的限制，既降低了对系统设计的要求，也可以通过提高发射功率或降低传输速率来增大传输距离。因此，超宽带混沌键控不仅是目前对超宽带通信技术研究的重要方向之一，也逐渐成为煤矿井下无线通信领域极具竞争力的技术[4]。

超宽带混沌键控按其解调方式的不同分为相干和非相干两类，基于非相干解调的差分键控由于避免了信道估计和载波同步，既可简化系统结构又能减少功率损耗。CD-DCSK、FM-DCSK等传统差分键控通过延时电路实现参考信号和信息信号在时域的正交，但目前接收机的宽带射频延时电路还难以实现低成本、低功耗的有效集成，通过两两正交的Walsh码序列实现参考信号和信息信号在码域正交的CS-DCSK应运而生[5]。尽管文献[6]己经给出CS-DCSK在高斯和瑞利信道下的性能分析，但其在煤矿井下信道环境的通信性能还不明确,由于地面的超宽带衰落信道模型和井下的传统传输信道模型对于煤矿井下超宽带通信系统不能完全适用，笔者根据井下环境特点建立超宽带多径衰落信道模型，研究CS-DCSK在井下巷道中的通信性能及传播特性，为煤矿井下实现高效可靠的超宽带通信提供更好的选择。

1 通信模型

1.1 发射模型

CS-DCSK发射模型如图1所示，混沌信号发生器输出的超宽带混沌信号设为x(t)，信息比特b经过双极性变换生成的信息信号设为a，Walsh码发生器1与Walsh码发生器2生成的Walsh码序列两两正交。在每一个比特间隔Tb内，超宽带混沌信号与Walsh码发生器1生成的Walsh码序列WP.N相乘作为参考信号，超宽带混沌信号、信息信号和Walsh码发生器2生成的Walsh码序列WO.N相乘作为信息信号，由此参考信号与信息信号通过两两正交的Walsh码序列实现码域的正交。

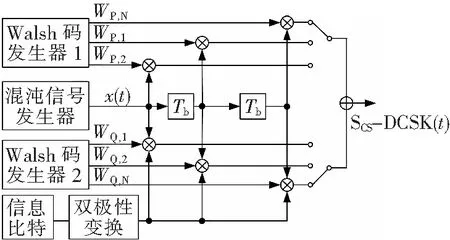
图1 CS-DCSK超宽带混沌键控发射模型

Fig. 1 CS-DCSK ultra-wideband chaos shift keying transmitting model

Walsh码是一种易于生成且具有优良自相关和互相关特性的正交码，一般可以通过哈达玛矩阵构建。假设信息信号的序列长度为N=2n，则N阶哈达玛矩阵为：

(1)

由式(1)可得，假设H1=[1]，则2阶、4阶、8阶和16阶的哈达玛矩阵分别为

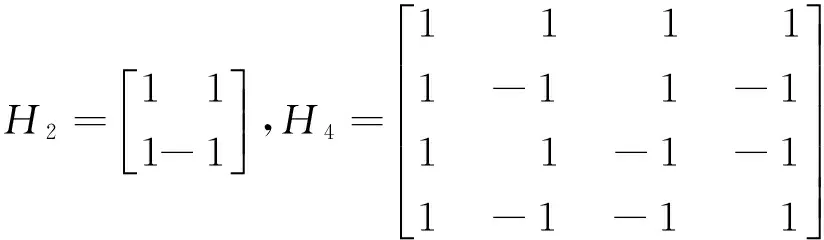
哈达玛矩阵的任意两行WN，i和WN，i都可以构成一个正交向量组，即可满足如下关系：

(3)

哈达玛矩阵的每一行代表一个Walsh码序列，假定只考虑传输单个符号的情形，经过CS-DCSK发射模型调制后发出的信号为

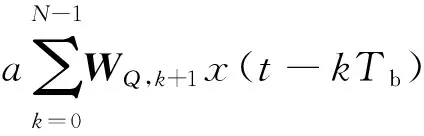
(4)

1.2 信道模型

井下巷道与地面室内多径环境不同，巷道为纵向受限空间且有许多障碍物，四壁有明显的粗糙度，存在大量的反射、散射和绕射路径。复杂的多径传播不仅会造成接收信号的大幅可变波动，也将形成严重的码间干扰[7]。尽管瑞利和莱斯分布能对井下无线信道的小尺度衰落进行很好的建模，但是大量传播实验表明，采用单一分布将不能准确描述不同传输环境下多径幅度分布的统计特性，而Nakagami分布能够提供与实际测试更好的匹配[8]。因此，文中采用Nakagami分布模拟井下超宽带通信的信道模型，其概率密度函数表示为

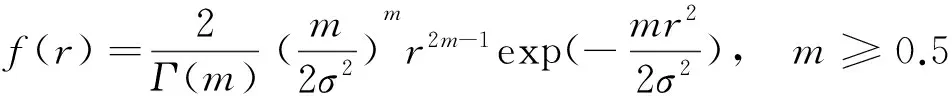
(5)

式中：Γ(m)——伽马函数；σ2——高斯分布的方差；m——形状因子或衰落指数。

Nakagami分布可以通过改变m值，描述具有不同统计特性的分布。当m=0.5时， Nakagami分布可以转化为单边高斯分布；当m=1时，Nakagami分布可以转化为瑞利分布；当0.51时， Nakagami分布与莱斯分布非常相似，并且它们的参数可以相互转换；当m=∞时，Nakagami分布可以转化为无衰落分布[9]。可见，采用参数可变的Nakagami分布能够更为准确地描述井下超宽带信道从轻度衰落到严重衰落等不同的无线传输环境。

1.3 接收模型

CS-DCSK接收模型如图2所示。

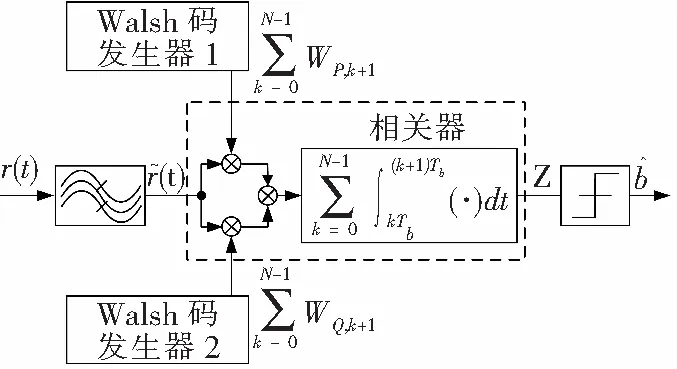
图2 CS-DCSK超宽带混沌键控接收模型

Fig. 2 CS-DCSK ultra-wideband chaos shift keying receiving model

假设信号在传输中受到加性高斯白噪声n(t)的干扰，则带通滤波器输出信号为

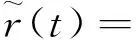
(6)

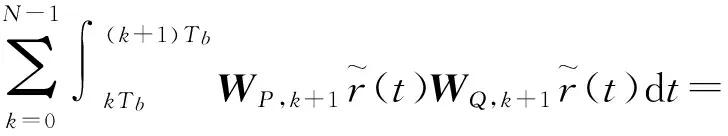
(7)

对判决统计量作门限判决，则可以得到传输信号的估计

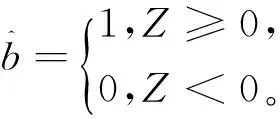
(8)

2 通信性能

为了研究超宽带混沌键控CS-DCSK在煤矿井下的通信性能，在Matlab/Simulink中对基于Nakagami信道的CS-DCSK通信模型进行仿真分析，得出系统参数对通信性能的影响，并与传统超宽带混沌键控FM-DCSK、CD-DCSK性能进行比较。

CS-DCSK误码性能随信道衰落的变化如图3所示。仿真时间T=3 000s，扩频因子M=8，Walsh码序列长度N=4，多径个数L=3，信道参数分别设置为高斯信道m=1、m=3，SSNR=Eb/N。通过仿真可以看出，在低信噪比情况下，信道衰落对CS-DCSK误码性能的影响非常微小；随着信噪比不断增加，CS-DCSK在高斯信道下的误码性能明显优于Nakagami信道，并且参数m反映了Nakagami信道的衰落程度，m越小衰落程度越深。

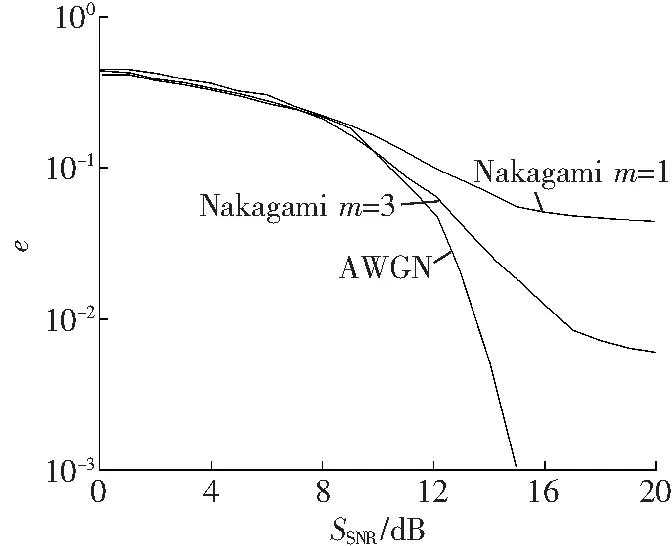
图3 CS-DCSK在不同信道衰落下的误码性能

Fig. 3 BER performance of CS-DCSK under different fading channels

CS-DCSK误码性能随多径个数的变化如图4所示。仿真时间T=3 000 s、Nakagami信道参数m=3、扩频因子M=32、Walsh码长度N=4，多径个数分别设置为L=1、2、3、4。在信噪比小于16 dB时，CS-DCSK在不同多径个数下的误码性能几乎完全相同；而在信噪比大于16 dB时，CS-DCSK作为一种扩频技术具有多径分集的能力，其误码率e会随着多径个数的增加而降低，并在L=3时误码率达到最低。但当多径个数继续增加时，由于多径增益无法弥补码间干扰则会导致误码率的降低。

图4 CS-DCSK在不同多径个数下的误码性能

Fig. 4 BER performance of CS-DCSK under different multipath numbers

CS-DCSK误码性能随超宽带混沌序列长度变化如图5所示，Nakagami信道参数m=1、扩频因子M=32、Walsh码长度N=4、多径个数L=1、混沌序列长度分别设置为T=50 000、100 000、200 000、300 000。在信噪比小于15 dB时，CS-DCSK在不同超宽带混沌序列长度下的误码性能没有区别；而在信噪比大于15 dB时，CS-DCSK误码率会随着序列长度的增加而降低，并在T=100 000时达到最低，但是随着序列长度的继续增加，CS-DCSK的误码率将呈上升趋势。

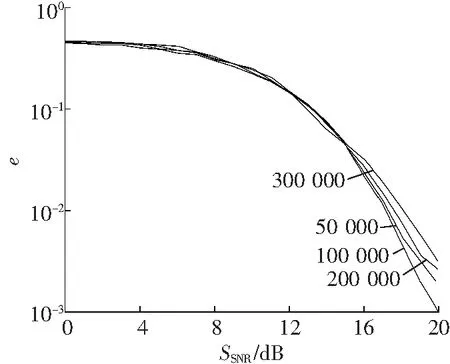
图5 CS-DCSK在不同混沌序列长度下的误码性能

Fig. 5 BER performance of CS-DCSK under different chaos sequence lengths

CS-DCSK误码性能随Walsh码长度变化如图6所示。仿真时间T=3 000 s、Nakagami信道参数m=3、扩频因子M=128、多径个数L=3、Walsh码长度分别设置为N=4、8、16、32。在信噪比小于10 dB时，CS-DCSK在不同Walsh码长度下的误码性能几乎完全相同；而在信噪比大于10 dB时，CS-DCSK误码率会随着Walsh码长度的增加而降低。这是由于当扩频因子M不变时，增大Walsh码长度会导致超宽带混沌序列长度减小，从而导致系统性能的下降。

图6 CS-DCSK在不同Walsh码长度下的误码性能

Fig. 6 BER performance of CS-DCSK under different Walsh code lengths

CS-DCSK与FM-DCSK、CD-DCSK在高斯信道下的误码性能如图7所示，仿真时间T=3 000 s、Walsh码长度N=4。在信噪比小于4 dB时， CS-DCSK的误码性能略好于CD-DCSK和FM-DCSK；在信噪比大于4 dB时，CS-DCSK的误码性能明显好于CD-DCSK和FM-DCSK，并且随着信噪比的增加，CS-DCSK的性能优势越加明显。

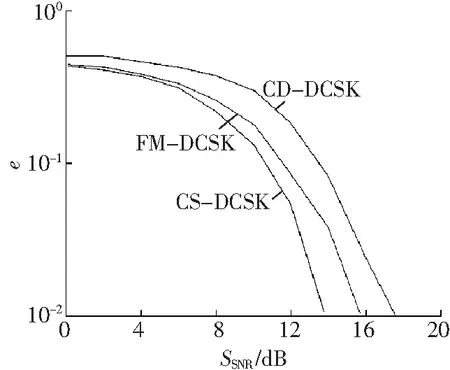
图7 CS-DCSK、FM-DCSK、CD-DCSK误码性能对比

Fig. 7 BER performance comparison of CS-DCSK, FM-DCSK, CD-DCSK

CS-DCSK误码性能在不同信道参数下随扩频因子的变化如图8所示。仿真时间T=3 000 s、Walsh码长度N=4、多径个数L=3，扩频因子分别设置为M=32、64、128、256。当信道参数分别设置为高斯信道m=1和m=3时，扩频因子变化对低信

a 高斯信道

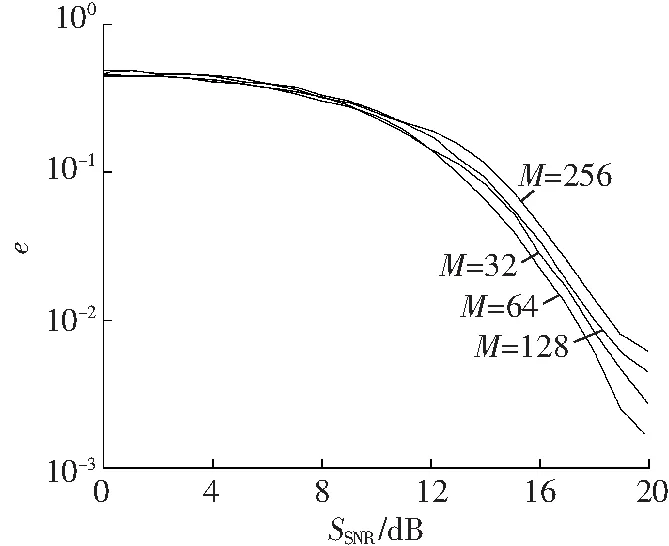
b m=1

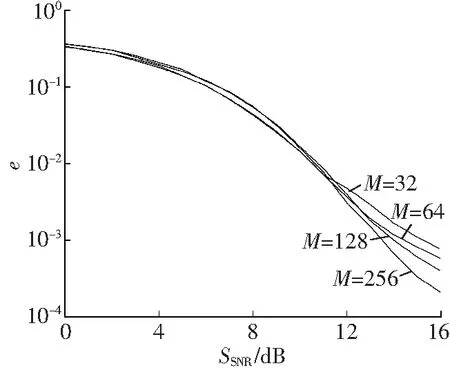
c m=3

d m=4

Fig. 8 BER performance of CS-DCSK under different spreading factors

噪比下的CS-DCSK误码性能几乎没有影响，随着信噪比的不断增加，高斯信道下的CS-DCSK在M=128时误码率达到最低，瑞利信道(m=1)下的CS-DCSK在M=64时误码率达到最低，莱斯信道(m>1)下的CS-DCSK在M=256时误码率达到最低。

3 结束语

适合的超宽带混沌键控模型是煤矿井下超宽带通信系统研究和设计的基础。由于Nakagami分布能够建模煤矿井下超宽带信道从严重衰落到轻度衰落等不同的传输环境，本文基于Nakagami信道模型仿真研究了CS-DCSK在井下巷道中的通信性能及传播特性，并比较分析了信道参数、多径个数和扩频因子变化对系统性能的影响，以及混沌序列长度与Walsh码长度之间的关系。同时，在信道、信噪比和扩频因子相同的情况下，CS-DCSK不仅能够克服FM-DCSK、CD-DCSK接收延时电路难以低成本实现的不足，其通信性能也优于FM-DCSK和CD-DCSK，因此可将其作为煤矿井下无线通信最有潜力的候选技术之一。

[1] 武兴佩， 王 琼， 李 萌. 超宽带无线通信技术的研究[J]. 信息通信， 2015(12): 1483-1489.

[2] 黄琼丹， 李 勇， 卢光跃. 脉间Costas跳频脉内多载波混沌相位编码需达信号设计与分析[J]. 电子与信息学报， 2015, 37(6): 1483-1489.

[3] 杨 华， 蒋国平. 一种改进型差分混沌键控通信方案[J]. 南京邮电大学学报(自然科学版)， 2013, 33(2): 29-33.

[4] 王 娟， 张 爽， 甄春阳， 等. 调频相关延迟差分混沌键控通信模型及性能[J]. 黑龙江科技大学学报， 2016, 26(5): 581-585. [5] 陈志雄， 黄 瑾， 徐位凯. CS-DCSK UWB与窄带通信系统共存性研究[J]. 重庆邮电大学学报(自然科学版)， 2013, 25(2): 259-264.

[6] Xu W K, Wang L, Kolumban G. A novel differential chaos shift keying modulation scheme[J]. International Journal of Bifurcation and Chaos, 2011， 21(3): 799-814.

[7] 康晓非， 朱代先. 煤矿井下超宽带信道建模与仿真[J]. 西安科技大学学报， 2010, 30(2): 241-244.

[8] 王艳芬. 矿井超宽带无线通信信道模型研究[D]. 徐州： 中国矿业大学， 2009.

[9] Nakagami M. The m-distribution-a general formula of intensity Distribution of Rapid Fading [M]. Oxford: Pergamon Press, 1960.

(编校 李德根)

Research on communication model and performance of ultra-wideband chaos shift keying in coal mines

WangJuan，LiJinfeng,NaYu

(School of Electronics & Information Engineering, Heilongjiang University of Science & Technology, Harbin 150022， China)

This paper is aimed at achieving an effective integration of lower cost and lower power consumption-an integration unattainable for the receiving delay circuit of traditional differential ultra-wideband chaos shift keying. The paper proposes the application of CS-DCSK ultra-wideband chaos shift keying with orthogonal code domain to realize the ultra-wideband communication in coal mine. The research is validated by simulating and analyzing the communication performance and propagation characteristics of CS-DCSK in coal mine roadway based on Nakagami multipath fading channel. The simulation shows that the BER performance of CS-DCSK is related to the fading index of Nakagami channel, multipath number and spread spectrum factor; and given the same channel, signal-to-noise ratio, and spread spectrum factor, CS-DCSK gives a better the communication performance than FM-DCSK and CD-DCSK, and can obtain an optimal system performance by a reasonable selection of parameters.

coal mine wireless communication； coal mine； ultra-wideband; chaos shift keying

2017-04-23

国家自然科学基金项目(61471158)；教育部高等学校博士学科点专项科研基金项目(20132301110004)

王 娟(1981-)，女，黑龙江省佳木斯人，副教授，博士研究生，研究方向：无线信号的传输处理及安全，E-mail：76115347@qq.com。

10.3969/j.issn.2095-7262.2017.05.021

TD76

2095-7262(2017)05-0555-05

A