延性材料中球腔膨胀模型及其解析解的进一步研究

高光发 李永池

摘要：空腔膨胀模型是当前广泛应用于许多工程领域的一个理论模型。基于Euler坐标构架，对球腔膨胀过程中不同阶段介质内的应力应变场的通解进行理论推导。讨论了当前国内外的一些推导成果的不足之处，分析表明当前的研究结果具有弹塑性解不连续、混淆了弹性体积压缩率和塑性阶段体积压缩率的概念等局限性，是一种间断的特解。给出了考虑塑性压缩性和塑性不可压两种情况下的弹塑性通解，在此基础上给出了考虑初始球腔尺寸和弹性变形等相关参数的准确的、连续的通解；并对塑性阶段压缩率的影响进行分析讨论。经过验证分析，这些通解更加普适，其简化及在特定假设下的特解与当前的国内外研究结果一致，该研究为球腔膨胀模型的应用和深化研究提供一定的参考。

关键词：球腔膨胀；空腔膨胀；应用力学；塑性力学

中图分类号：O39文献标志码：A文章编号：1672-1098（2017）03-0006-11

Abstract：The cavity expansion model is widely used in engineering area. The deficiencies and problem of the corresponding solutions in the published literatures， such as discontinuity between the elastic stage and plastic stage and confusion of some concepts， were analyzed and discussed. The general solutions of the relative size of the plastic zone and field of stress in the Euler coordinate system were deduced， in which the initial cavity size and the elastic deformation prior to the plastic deformation were considered. These solutions are verified that they are continuous and universal and the solutions in the published literatures are the special solutions. It can be referred to in the appllication and further study the cavity expansion model.

Key words：spherical expansion； cavity expansion； applied mechanics； plasticity

空腔膨胀模型自提出至今无论是土木工程、矿业工程还是军事工程都得到了广泛的应用与推广，自从空腔膨胀模型首次被引入杆弹对金属类延性靶板的准静态/动态侵彻行为分析[1]半个多世纪以来，得到更多力学学者的关注和研究。在此创新性的工作[1]基础上，文献[2]考虑了材料的可压缩性，并推导出此种情况下的空腔膨胀模型中相应的物理量的计算式；同时，文献[3]以另一种方法推导出考虑材料壓缩特征的空腔膨胀模型中相关物理量的解析解。文献[4]对二战期间空腔膨胀模型的研究成果进行了综述。之后，文献[5]对匀速球腔膨胀问题进行了分析，文献[6]根据实验观察对空腔膨胀模型进行了分析，文献[7]对金属材料中空腔膨胀非稳定性进行了研究。在侵彻力学理论研究方面，文献[8-10]对考虑材料压缩性情况下动态空腔膨胀问题进行了系列的研究讨论，特别地，在延性材料的抗侵彻问题中，动态空腔膨胀得到许多学者[11-19]的应用和推广。文献[20]对空腔膨胀模型进行了总结和研究。虽然当前在此方面的研究众多，但各研究之中存在许多不统一之处，各有优缺点，例如，一般以拉为正，但有些研究以压为正，有些在Euler坐标系下进行推导[20-23]，也有点在Lagrange坐标系下进行推导[4]。这在很大程度上限制了空腔膨胀模型在工程中的应用。

对金属延性材料中球腔膨胀模型的研究已经有半个多世纪了，然而除了存在上述所提的问题之外，当前的研究还存在一些不足之处：首先，在膨胀过程中存在弹性压缩和塑性压缩两个过程，因而在不可压缩假设过程中应区分两种情况下的区别，也需要考虑应变包含弹性应变和塑性应变这一事实，这点在当前的一些研究中没有体现；其次，绝大部分研究所计算出的塑性区域相对尺寸是一个固定值，事实上，这个没有体现压缩过程中的实际情况，从而导致其弹性解与塑性解之间不连续。本文参考当前国际对球腔膨胀模型的研究，在讨论分析当前的相关研究中的不足之处和待改进之处，借鉴当前学者的研究方法，给出系统的、思想统一的和较易理解和应用的一种新的推导过程与结论。

1球腔膨胀模型的弹性解

在无限介质中，内部球形内腔由于压力向外部呈球形膨胀，初期周边只有弹性变形，但随着内部压力的增大，从而形成最内部为塑性变形、外部为弹性变形、无限远处可认为无变形等三个区域。利用弹塑性力学，可以求出球腔内表面及介质内部的压力等相关参数。

1.1弹性解的推导

在无限弹塑性介质中，若初始球腔压力为0，此时向球腔内表面缓慢施加作用力，使得材料变形行为为准静态，在初期，材料中的应力状态应为弹性状态。

对于球腔膨胀模型，则有应力平衡方程

即当球腔膨胀到a0+Δa时，介质中才开始出现塑性压缩行为。

1.2弹性解的分析与讨论

在上述准静态球腔膨胀模型的弹性解的推导过程中，整个过程并没有假设弹性不可压，完全根据弹性理论进行推导，所以也应适合于弹性可压缩即泊松比不为0.5时的情况，所以该弹性解为准静态球腔膨胀模型中线弹性材料的解。而从式（6）可知

即体应变为0。在整个推导过程中只有一处假设，即小应变假设，忽略了真应变中的高阶项，而体应变恰恰是径向和环向应变的高阶小量，所以出现此结果；而且，从推导结果来看，小应变假设是合理较准确的，所以该解也是合理准确的，适合与可压缩和不可压缩两种情况的。

2塑性不可压介质弹塑性解

不可压缩假设应包含两个意义：弹性不可压和塑性不可压。前者一般存在误差，因为金属材料的弹性阶段的泊松比v一般明显小于0.5，如普通45号钢为0.29，所以在压缩过程中密度会逐渐增大，但由于其弹性应变极小，所以此类假设虽然理论上不正确但计算结果误差较小；后者在一般压缩过程中基本成立，在很多屈服准则中，假定金属类材料塑性不可压，只是在高速侵彻和爆炸过程中由于高温高压条件下，才考虑其可压缩性。另一方面，应变也包含弹性应变和塑性应变部分，总应变可假设为两种应变之和。

相对于其他学者的推导过程，文献[20]的推导过程较为简洁易懂，只由Euler坐标系下的质量守恒方程方程推导出相关解，但其假设介质弹塑性皆不可压，因此推导过程与结论稍显粗糙；文献[6]直接给出塑性相对尺寸，虽然在塑性区域相对尺寸的结果中存在泊松比参数，但推导中并没有完全体现弹性压缩等现象。

2.1塑性不可压缩介质中的塑性区域相对尺寸

在上节的弹性区域内应力等量的推导过程中，假设应变极小从而满足小应变理论，结果表明该假设是合理可行的；而在塑性变形中，其应变往往不一定能够满足该理论，而且很多时候其应变值很大；因此，此时应变不能取值为Cauchy应变，而应为真应变。根据文献[4]的推导结果，有式（13）推导的是塑性阶段的质量守恒方程，需要注意的是ρp0表示介质中刚达到塑性变形时的初始密度，而不是整个阶段包括弹性变形的初始密度，如图1所示。

从图1可以看出，从ρp0变化ρp至经历两个主要阶段：首先，塑性变形从内边界传递到物质坐标r-u处，此阶段内，此阶段的变形为弹性变形；其次，该点运动到瞬时坐标r处，此阶段的变形为塑性变形。在弹性阶段，介质的体应变为径向和环向应变的高阶小项，所以其中极小，再根据塑性不可压假设，可认为两者之间的值相等，所以其比值为1。然而此时，其边界条件并不是当前现有研究中的u（a）=a-a0（为a0初始球腔半径），因为塑性阶段的位移是从介质达到弹性极限时开始计算的，根据式（10）可知，在塑性阶段开始时， 球腔内壁半径已经膨胀了Δa，因此其边界条件应为u（a）=a-a0-Δa，根据式（13），可有上式说明，球腔内径膨胀到a≥a0+Δa时才开始出现塑性变形，即此时才有c≥0，而不是当前文献中，a≥a0时就出现塑性变形，这与球腔膨胀过程中的物理过程相符。其次，以上述的45号钢为例，其屈服强度为355MPa，泊松比为0.29，杨氏模量为206GPa，两者之间的关系如图2所示。图2中对不同弹性屈服应变时塑性区域相对尺寸之间的关系进行了描述，其中泊松比取为0.29。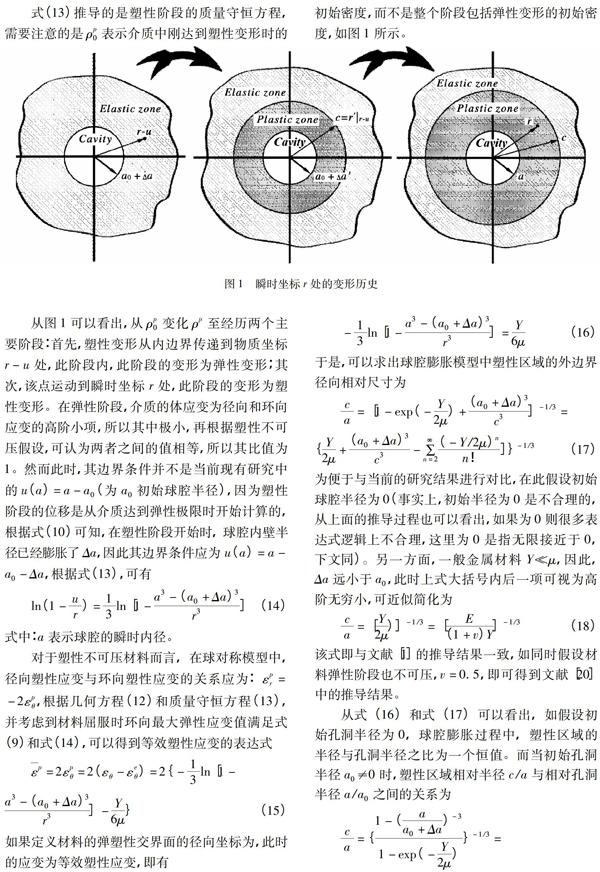

由圖2（a）可知，在球腔膨胀初期，随着孔洞的增大，塑性区域尺寸迅速增加，但当孔洞直径增大到原有的两倍之后，塑性区域的相对尺寸基本恒定，并不明显随孔洞尺寸的增加而增大[1，20]；影响塑性区域最终相对尺寸的最大因素是材料的弹性屈服应变。而从图2（b）可知，塑性区域的相对尺寸一直为弹性碰撞，内径到达a=a0+Δa后才逐渐出现塑性区域，之后逐趋稳定，与时间情况是吻合的，而且该解能够与弹性解保持连续性。

同样，以上文的45号钢为例，对比本文的推导结果与当前研究结果，如图3所示。

从图3可以看出，当球腔膨胀相对内径大于3.5之后，本研究的结果与文献[1]的研究结果基本一致，且皆大于文献[20]的简化结果，即说明考虑弹性阶段的可压缩性所得到的塑性区域相对尺寸稍大于不可压缩假设下的结果。

2.2塑性不可压缩介质中的球腔内壁压力

如式（7）所示，当球腔内边界压力大于时，材料进入屈服阶段。如图1所示，此时在邻近球腔内边界区域首先形成塑性区，较远区才为弹性区域。对于一般金属材料而言，在准静态加载作用下，其应变率及塑性变形导致的温升都极小，可以不予考虑。因此可简单的认为塑性阶段材料中的等效应力取决于其初始屈服强度和等效应变。

上式简化结果与文献[1]的研究结果一致，其一般连续解为式（36）。

3塑性可压介质弹塑性解的推导与分析

3.1准静态理想弹塑性性介质中球腔膨胀模型弹塑性解初解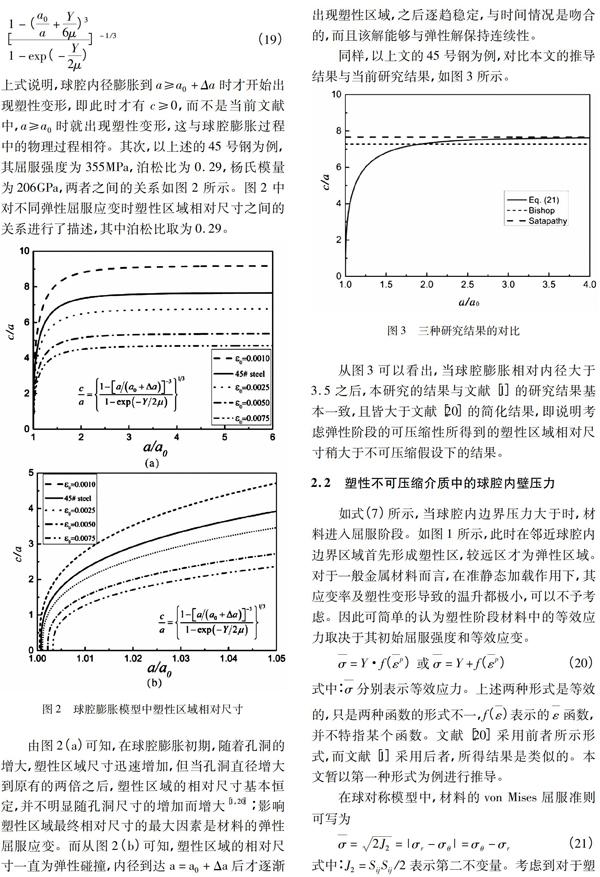

式（48）和式（49）即考虑塑性压缩效应时塑性区域相对尺寸和球腔内表面压力的解析表达式的通解和特殊情况下的解；其中特殊情况下的解与当前国内外研究和使用的解析公式一致。利用上述所推导出的模型，可以对考虑与不考虑材料压缩性能时球腔膨胀模型时的相关参数进行对比，以45号钢为例，不考虑材料压缩性时塑性相对尺寸的计算结果比考虑材料压缩性时的结果高约12%，其内表面的压力高约5%。

3.2初解存在的问题分析

上述考虑塑性可压缩效应时的解得到大量的应用，并在此基础上推导出其他更复杂本构模型时的解析表达式和动态球腔膨胀下的解。从上述的结果分析来看，考虑塑性压缩性时45号钢所得的解明显小于塑性不可压假设前提下的对应的解。从上述的推导方法可以看出，主要基础就是式（42）所示的质量守恒方程，然而，在其基础和推导过程中存在以下几个概念性的问题：

上二式與式（48）（49）一致，说明当前通用的结论中没有区分弹塑性阶段的体积压缩率，混淆了其概念。而本推导与当前推导的基础除此处修改外，还有一项是本推导考虑到密度增加是从球腔出现塑性变形开始，即压力为当前压力与弹性屈服点压力之差，但结果与前文研究结果一致。原因如下：前文的第一种推导过程中利用屈服条件Y=σθ-σr，使整个计算纳入塑性范畴，在此方面两者推导结果一致，但该修正是具有物理意义的。

以45号钢为例（同上忽略初始球腔尺寸），则其塑性区域相对尺寸和球腔内表面的压力随塑性泊松比的值如图5所示。

图5塑性区域相对尺寸与内表面压力随塑性泊松比的变化趋势从图5中可以看出，以45号钢为例，考虑塑性变形阶段介质的可压缩性会减小塑性区域相对尺寸以及球腔内边界压力的值，但考虑到金属延性材料的塑性压缩率远小于弹性压缩率，其减小的幅度小于文献[20]。

4结论

空腔膨胀模型自从提出以来，在许多工程领域得到了广泛的应用。本文针对准静态球腔膨胀模型，参考借鉴当前国内外的研究思想，对球腔膨胀过程介质中的弹性应力状态及相关参数的求解进行了推导，并分别在Euler坐标系中对考虑塑性阶段材料的压缩率和不考虑其压缩率两种情况下的相关参数解进行了推导和讨论，校正了当前推导过程中的一些不足之处。主要结论如下：

1）分析表明，在弹性解的推导过程中，小应变假设是合理和较准确的；然而，由于体应变是径向和环向应变的高阶小量，从而导致小应变假设中体应变被忽略。因而，球腔膨胀模型中，弹性解具有普适性，对于考虑塑性压缩性和不考虑塑性压缩性情况时其解基本一致。

2）在塑性不可压假设下，考虑了弹性压缩阶段的压缩性和初始球腔尺寸，得到了塑性相对尺寸和球腔内壁压力的连续的通解。该解考虑了塑性变形时球腔内已具备的弹性应变，也考虑了初始球腔尺寸不为0的情况，描述了球腔膨胀塑性变形初期相关参数如塑性尺寸、内壁压力随球腔尺寸变化的规律；同时，该塑性解能够与弹性解保持很好的连续性，并对几种典型材料本构模型时的具体解进行了分析讨论。最后，将该解与当前国内外文献中所求得的常用解进行了对比分析，分析表明，当前文献中的解为本文所推导出的解的特解。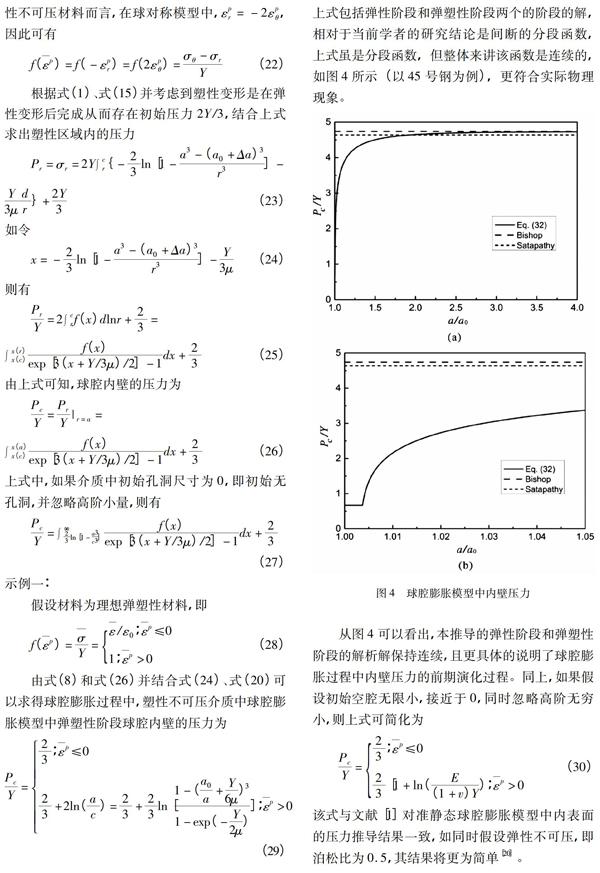

3）在考虑介质可压缩性的前提下，借鉴当前学者的推导思想，给出了Euler坐标系中的相关解，并对改进进行了讨论分析。然而，当前解存在两个问题：一为与塑性不可压假设下的解不连续，二为弹塑性阶段泊松比概念模糊。分析表明，实际上此两个问题的根源就只有一个问题，即在推导中混淆了弹性体积压缩率和塑性阶段体积压缩率的概念。在此基础上对其进行了推导，得到了考虑初始球腔尺寸和塑性变形前的弹性应变等情况下的通解，结果表明，该解与不考虑塑性变形下的结果连续，即假设塑性阶段的泊松比为0.5时，两解一致，解决了当前解存在的问题；并给出了相关解随塑性泊松比的变化而改变的规律，对比分析显示，当前通用解是该解的一种特解。

本文中的所有推导都是基于Euler坐标完成的，推导过程中参考了当前国内外相关的思想，并对其进行简化，推导结果为球腔膨胀模型的通解，适用情况更加广泛，为工程应用提供了一定的参考作用。

参考文献：

[1]BISHOP R F， HILL R， MOTT N F. The theory of indentation and hardness test[J]. The Proceedings of The Physical Society， 1945， 57（3）： 147-159.

[2]HILL R.The mathematical theory of plasticity[M]. Oxford： Oxford University Press， 1950.

[3]CHADWICH P. The quasi-static expansion of a spherical cavity in metal and ideal soil[J]. The Quarterly Journal of Mechanics and Applied Mathematics， 1959， 12（1）： 52-71.

[4]HOPKINS H G.Dynamic expansion of spherical cavities in metal[M]// Progress in Solid Mechanics. Amsterdam：North-Holland Publishing Co.， 1960：284-286.

[5]HUNTER S C， CROZIER R J M. Similarity solution for the rapid uniform expansion of a spherical cavity in a compressible elastic-plastic solid[J]. The Quarterly Journal of Mechanics and Applied Mathematics， 1968， 21（4）： 467-486.

[6]WRIGHT S C， HUANG Y， FLECK N A. Deep penetration of polycarbonate by a cylindrical punch[J]. Mechanics of Materials，1992， 13（4）： 277-284.

[7]HUANG Y， HUTCHINSON J W， TRERGAARDV. Cavitation instabilities in elastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids， 1991， 39（2）： 223-241.

[8]FORRESTAL M J，LUK V K.Dynamic spherical cavity-expansion in a compressible elastic-plastic solid[J]. Journal of Applied Mechanics，1988， 55（2）： 275-279.

[9]FORRESTAL M J， OKAJIMA K， LUK V K. Penetration of 6061-T651 aluminum targets with rigid long rods[J]. Journal of Applied Mechanics，1988， 55（4）： 755-760.

[10]FORRESTAL M J， TZOU D Y， ASKARI E， et al.Penetration into ductile metal targets with rigid spherical-nose rods[J]. International Journal of Impact Engineering， 1995， 16（5）： 699-710.

[11]TATE A. A theory for the deceleration of long rods after impact[J]. Journal of the Mechanics and Physics of Solids， 1967， 15（6）：387-399.

[12]TATE A. Further results in the theory of long rod penetration[J]. Journal of the Mechanics and Physics of Solids， 1969， 17（3）： 141-150.

[13]GOODIER J N.On the mechanics of indentation and cratering in solid targets of strain-hardening metal by impact of hard and soft spheres[C]// AIAA Proceedings of the 7th Symposium on Hypervelocity Impact III， New York：AIAA，1965： 215-259.

[14]HANAGUD S， ROSS B. Large deformation， deep penetration theory for a compressible strain-hardening target material[J].AIAA Journal，1971，9（5）：905-911.

[15]PARTOM Y. Cavity expansion model for partially confined targets[C]// 16th International Ball Symposium， San Francisco： CA， 1996：421-426.

[16]ROSEBERG Z， TSALIAH J.Applying Tate's model for the interaction of long rod projectiles with ceramic targets[J]. International Journal of Impact Engineering， 1990， 9（2）： 247-251.

[17]ROSENBERG Z， MARMOR E， MAYSELESS M. On the hydrodynamic theory of long-rod penetration[J]. International Journal of Impact Engineering， 1990，10（1）： 483-486.

[18]WALKER J D， ANDERSON C E. A time-dependent model for long-rod penetration[J]. International Journal of Impact Engineering， 1995， 16（1）： 19-48.

[19]LEE M， BLESS S.Cavity Dynamics for Long Rod Penetration[R]. Austin：University of Texas， 1996.

[20]SATAPATHY SS. Application of cavity expansion analysis to penetration problems[R]. Austin：University of Texas， 1997.

[21]CHADWICK P.The quasi-static expansion of a spherical cavity in metals and ideal soils[J].The Quarterly Journal of Mechanics and Applied Mathematics， 1959， 12（1）： 52-71.

[22]MENDELSON A.Plasticity： theory and applications[M].Florida：Krieger Publishing Co.，1968：102-103.

[23]FORRESTAL M J， LONGCOPE D B.Target strength of ceramic materials for high-velocity penetration[J]. Journal of Applied Physics， 1990， 67（8）：3 669-3 672.

[24]LUK V K， FORRESTAL M J， AMOS D E. Dynamic spherical cavity expansion of strain-hardening materials[J].Journal of Applied Mechanics，1991， 58（1）： 1-6.

[25]CHADWICK P， COX A D， HOPKINS H G. Mechanics of deep underground explosions[J].Philosophical Transactions of the Royal Society B Biological Sciences，1964， 256（1 070）： 235-300.

（責任编辑：李丽，编辑：丁寒）