变与不变彰显数学的智慧

潘箐

【摘 要】本课以“变”与“不变”为主线，让学生在找“变”的过程中，找到“不变”。“变”与“不变”，从最初大量信息的观察、计算、分析，至剥丝抽茧地聚焦新学内容，再到由数到图的不同表达，始终贯穿每一个环节。在这样整体视野中，学生不仅形成一个突出反比例、清晰其他几种关系的网络，学会找"变"与"不变"的方法，更是养成了对事物、对生活的态度。这样的数学课堂除了用最为本质的数学问题、数学关系、数学特点等吸引学生外，更是启迪了学生的智慧，从而也让数学课堂更有魅力。

【关键词】变与不变；整体；智慧

中图分类号：G622.0 文献标识码：A 文章编号：1671-0568（2017）22-0021-03

“认识反比例”一课是“苏教版”小学数学六年级（下册）总复习前的最后一个内容。这一课与“正比例”的认识一起，编排在比和比例及常见的数量关系的基础上，渗透函数思想，为学生后续的函数学习打下基础。由于“反比例”概念与“正比例”的类似，有了“正比例”的学习经验和基础，学习起来已不能成为难点，其教学的过程如若还以常用的正比例教学方法——“在几个正比例事例的观察比较发现中，抽象共同特征，再予以判断和应用加深理解”进行教学，一来有重复之嫌，学生学习容易疲惫，二来也没有真正地发挥这一内容的优势，更好地激发学生的思考。

细细梳理这一课内容，不难发现，当下教师所熟知的“数感”“符号意识”“数据分析观念”等诸多核心词，分类思想、对应思想、函数思想等多种数学思想方法或观察、比较、抽象、概括等思维方式都能以其为载体渗透一二。内容丰富无比，却不能面面俱到，着眼何处才能让学生有更多收获？“万物皆变”，这是哲学的基本理念。而既有变，也定有不变。“反比例”这一内容的两个要素“一个量随着另一量的变化而变化”和“积不变”正好对应“变”与“不变”的思想。“变”与“不变”为主线，既锁定主要教学内容，利于创设良好的认识环境，也能让学生多一些哲学高度的思考。因此，在智慧数学团队各位专家和同仁的指导下，笔者就“反比例”这一内容的教学作了一番尝试。

一、计算分类，感受丰富的“变化”

生活中，有着形形色色、各式各样的数量关系，每组关系中的变化也是千姿百态。反比例关系只是众多数量关系里的一种。典型的数量关系有着怎样的不同？不同种类的数量关系又分别具备怎样的特征？具备不同特征的各类又如何命名？

人们对事物的认识，往往从区分事物开始。要区分就会有比较，并有了在此基础上的分析与分类。在纷繁复杂的大量“变化”中，选择需要的“变化”进行比较、分类等，既让学生亲历了“反比例”概念的形成过程，也让学生有了找“变化”的体验。

【片段一】

師：老师带来了七组相关联的量。出示：

（1）妈妈和儿子的年龄如下：

（2）一辆汽车，行驶的时间与路程。

（3）用20㎝的线围出的长方形的长与周长如下：

（4）一本书，每天读的页数和读的天数如下：

（5）一本书，已读的页数和剩下的页数。

（6）一辆汽车，从A地到B地行驶的速度和时间如下：

（7）正方形的边长和周长。

师：请大家先填一填表格，再找一找，7个表格中，两种相关联的量同时变化的有哪些？

生：（1）（2）（4）（5）（6）（7）

师：为什么没选（3）呢？

生：周长没变的时候，长却在变化，所以它们不是同时变化的。

师：也就是说，相关联的量有的会同时变化，有的不同时变化。没有同时变化，今天我们暂时不研究。还剩六组，这里的每组相关联的量都在同时变化。同时变化，又可以分成哪几类呢？

生：可以分成同时变大、同时变小、一种变大一种变小、一种变小一种变大。

师：六组数据被分成了四类，如果再归归类，把它们分成两类，你还会再分吗？

生：同时变大或变小，一种变大，另一种变小。

……

七组熟悉数据的计算与观察，不仅让学生体会到数量关系的丰富，更在填写中让学生对每种量的大小变化有了初步的感知，也为后面“不变”量的发现做好了准备。除此以外，学生也在对各组数据的观察区分中，感受了人们认识世界的一般方法，领略了一般概念的初期形成过程，同时，也在数据的变大变小中，提升了学生数感，凸显了这一板块找“变”的主旋律。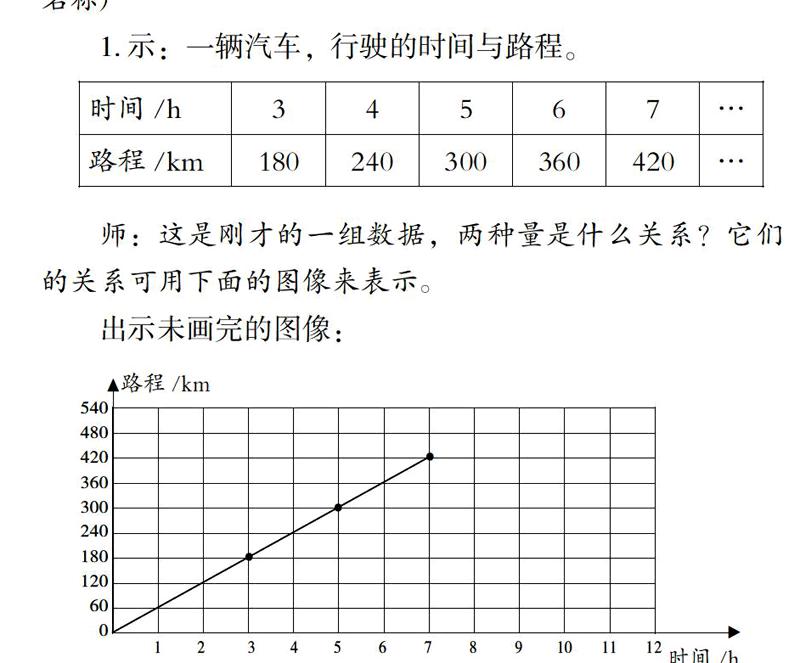

二、猜想概括，在“变化”中寻找“不变”

“变”与“不变”相互依存，有“变”也定有“不变”。因此，找完“变化”，便在“除了变化，还有什么？”“除了之前学过的‘商不变，还有什么不变？”的追问下，让学生从观察前面的“变化”关注寻找“不变”，又由找“不变”聚焦到找“积不变”，从而为学生正式认识“反比例”抽取了素材。

1. 在“正”与“反”的猜想中，聚焦“积不变”

【片段二】

师：同时变化的是相关联的量，还要有不变，想想看，咱们在哪接触过这样的内容？哪些表格中能找到正比例关系？出示：表格（2）（7）

师：你们怎么知道这里的每组量是成正比例关系的呢？第二个表格呢？

师：这两个表格中都有什么不变？

生：商不变。

师：六组数据，我们在两组中找到了“商不变”。还有四组，它们中还有不变吗？

出示：除了商一定，还有其他“一定”吗？

师：仔细观察，跟同桌的伙伴互相说一说：你发现了哪些一定？怎么发现的？endprint

师：算一算，让我们找到了变化中的不变。

师：商一定，就有了正比例关系。有正比例，你觉得还会有什么？

生：反比例。

师：正比例关系中有商一定，那反比例呢？

师：为什么都选“积一定”？

生1：因为积和商相对。

生2：我觉得有乘就有除，乘除是逆运算。

师：很有道理！事实上，确实如此！商一定有了正比例，积一定就有了……

……

數学有其独特的美，其中对称是数学美的核心。有“正”就有“反”，有“除”就有“乘”，有“商”就有“积”……这类相对、相反的思考不仅引出了后继的学习，也让学生领略了数学的对称美，渗透了人们看待事物的辩证眼光，以此引出“反比例”，让学生聚焦“积不变”。

2. 在“变”与“不变”的概括中，认识反比例

【片段三】

出示：

师：仔细观察一下这两个表格。谁来说一说，每组中，变化的是什么？不变的又是什么？同桌互相说一说。

师：先来看（4）号表格。读的天数在变化？每天读的页数也随着……

生：也随着变化。

师：每天读的页数是随着什么的变化而变化的呢？

生：每天读的页数也在随着天数的变化而变化。

师：什么不变？总页数是多少，你怎么算的？

生：用读的天数乘每天读的页数，40×6=48×5=60×4=80×3。

师：对，也就把相对应的两个数乘起来。

师：（6）号表格中呢？总路程又是多少呢？……

师：比较一下每组中两个量变与不变的情况，发现它们共同的地方了吗？

生：都有两组相关联的量，相对应的两个数乘起来积不变。

出示：两种相关联的量，相对应的两个数的积一定，这两种量就成反比例关系，这两种量就是成反比例的量。

“一个量随着另一量的变化而变化”和“两个量相对应的数的积不变”是反比例关系的两个要素。“每天读的页数是随着什么的变化而变化的呢？”“总页数是多少，你怎么算的”“发现它们共同的地方了吗？”之类的有关“变”与“不变”的问题，既放慢了学习节奏，加深了学生的理解，也在抽象概括中有效地训练学生的思维，并渗透函数思想和“对应数相乘”的对应思想。

至此，从一开始对“变”的“批量”观察、分类，到这里对“不变”的“聚焦”分析、比较以及抽象、概括。学生完整地感受了人们认识事物的一般过程，体验了人们认识事物的一般方法，也经历了观察变化并在变化中寻找不变的思考过程。

三、数形对应，不同表达中的“变”与“不变”

变化与不变无处不在。反比例关系在数据表达、文字表达和解析表达之后，还有着形象的图形表达。两种量的每组对应数据都能用二维图像中的一个点来表示，反过来，图像中的每个点也对应着一组数据。图像中亦存在着与数据相同的变化情况，在同一关系的不同表达中继续寻找“变”与“不变”，既让学生进一步认识图像的意义，提升读图用图的能力，也能进一步深入体会“变”与“不变”的随处可寻。

【片段四】

师：我们也能把变与不变在图形中表示出来。（板块名称）

1. 示：一辆汽车，行驶的时间与路程。

师：这是刚才的一组数据，两种量是什么关系？它们的关系可用下面的图像来表示。

出示未画完的图像：

师：如果继续往下画会是什么图形？只看图像能看出什么变了？什么没变？这里的速度等于多少，谁会算？数据在哪里？图中每一个点都对应着一组数据。

再出示：

师：这里两种量分别用x、y来表示。什么在变？看到不变了吗？它们成什么关系？

师：正比例关系可以用一条直线来表示，反比例呢？想象一下，也可以比划比划。谁来猜一猜？

师：既然有数据，我们就一起来找点画一画。还是一条直线吗？不直就只能……？连线成图。有直就有曲，数学里面把它叫曲线。

师：现在从图形里能看出变化的是什么？没变的呢？x扩大，y反而……反过来，x缩小，y反而……

师：如果继续画下去，曲线会离x轴越近还是越远？离y轴呢？为什么？不管怎么变，什么一直没变呢？

……

从学生熟悉的数据表达，到概括出的文字表达和解析表达，再到形象而简洁的图像表达，表达形式由具体到抽象，由单一到概括，由纷繁到凝练，数学的抽象概括、简洁凝练在不同的表达中再次让学生有所体会。

除此以外，在图像中继续寻找变与不变，既让学生关注数据与点的对应，学会了读图，也让学生空间想象有了抓手，可以根据每组数据的特点和点的位置变化趋势去进行“当一种量很大时，另一量会怎样”的预测，从而更好地理解“变化”的相关联。

纵观整节课，学生感受体会了找“变”的过程，并在“变”中找到“不变”。“变”与“不变”，从最初大量信息的观察、计算、分析，至剥丝抽茧地聚焦新的学习内容，再到由数到图的不同表达，始终贯穿每一个环节。

在这样的整体视野中教学，学生不仅容易在心中形成一个突出反比例、清晰其他几种关系的网络，学会了找变与不变的方法，更是养成了一个对事物、对生活的态度：千变万化的事物或生活，有着什么样的变化？这些变化存在规律吗？有什么样的规律，又能帮助我们有着怎样的新发现呢？一节课如若让学生能有这样的理性思考，那数学课堂除了用最为本质的数学问题、数学关系、数学特点等吸引学生外，更是启迪了学生的智慧，从而也让数学课堂更有魅力。

（编辑：胡 璐）endprint