简单电磁问题分析中的举一反三

谭康伯， 路宏敏， 苏 涛

(西安电子科技大学 电子工程学院， 陕西 西安 710071)

简单电磁问题分析中的举一反三

谭康伯， 路宏敏， 苏 涛

(西安电子科技大学 电子工程学院， 陕西 西安 710071)

根据本科高年级电磁相关专业研究型教学实际情况，在有关电磁基本概念、基本原理、基本方法的基础上适当引伸，以电磁学中的一个简明静场问题为例，对电磁数值分析教学中的三种重要方法：差分法、矩量法、有限元进行了讨论分析。通过举一反三，进一步启发研究型教学中的问题处理多样性。

电磁；静场；数值分析

0 引言

在本科专业教学中，一个重要的要求就是不断引导学生构建专业知识框架和联络。对电磁专业研究型教学而言，在基础知识教学时，对基本概念、基本原理、基本方法(本文简称三基)等相关内容提出了相当高的要求。不仅仅要求能通过教学认识基本规律，还要能从中启发灵活、多变的思想和方法来促进对于后续可能遇到的实际问题的分析和解决。基础知识教学作为坚实的树根和树干，需要为后续专业知识教学的树冠上丰富多彩的内容提供支撑。灵动的思维是学生进行高阶段深入学习、研究和工作的有力促证。正因为如此，在电磁相关专业研究型教学中，从简单问题出发，不断引伸、扩展、深入、联系是非常重要的。

对此，本文以相应电磁三基知识框架为出发点，以简单的二维静场问题为例，着重探讨了基于同一问题的发散型分析方法，举一反三，加强和促进对问题处理多样性的理解，进而表明在电磁教学实践中，基本概念、基本原理、基本方法基础之上的适当引伸对于基础教学与研究型教学间联系和启发的重要性。

1 问题模型的基础

静电场是指相对于观察者静止的电荷产生的场。从历史的角度来看，人类在对于静电问题的实践过程中，由“定性”—“定量”的认识飞跃过程是科学发展的必然，其中卡文迪许、库仑、高斯等伟大的科学家为此做出了巨大的贡献。定量分析必须借助于数学手段。由基本定义可知，静电场不随时间变化，故需关注其空间分布特征。静电场是一个矢量场，于是从矢量分析的角度就需要对其所对应的旋度和散度进行讨论。对此，静电场的数学特征可以总结为

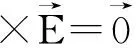
(1)

式(1)表明对于静电场性质特征的认识。旋度特征描述了静电力是保守力，静电场是无旋场。散度特征则表示电荷所产生场区的分布特性，真空中任意一点的电场强度的散度等于该点的电荷密度与介电常数之比。若场区为无源自由区，那么根据矢量分析中的重要关系：梯度场无旋，以及电磁学知识引入的电位φ的定义，则通过对上面两个关系的考虑，就可以进一步得到相应静电场问题的支配方程：

▽2φ=0

(2)

其中，▽2为Laplace算子。如果不只是停留在这些一般性的定性认识基础上，需要进一步关注具体静电问题的分布特征时，就需要定量处理。

2 问题分析的原理

一般而言，在电磁场中，“支配方程+边界条件”构成了相关电磁问题的分析解决方案。具体求解方法包括：解析法、半解析法和数值法。随着计算机技术的发展，数值法已成为一种非常实用且重要的分析方法。相关电磁问题的求解实际上是电磁科学和计算科学的共同体，两者是通过工程数学有机结合起来的，而矩阵(Matrix)在中间发挥了突出作用。简言之，电磁数值方法的关键作用就是将相关“支配算子方程”转化为“矩阵代数方程”。

3 问题的分析处理

3.1 问题模型建立

在电磁场中，静电问题有其简洁的特点，虽然与其相关问题及处理具有特殊性，但其中所反映的思想、原理并不失一般规律。首先建立一个简单的2D静电问题模型。在二维空间中，设有一方形区域，简单起见，取区域四边边长各为3，上边电位为100 V，其它三边为0 V，求其中待求场区的电位。下面将具体围绕该问题来展开数值分析和讨论。

3.2 途径1—差分法

采用有限差分法对该问题分析。该方法处理问题的一个关键是：实现微分到差分的转化。由前面基础理论可知，该问题的支配算子方程为Laplace方程，在2D情况下可以进行微分～差分(转变)处理：

▽2φ=0

～

～

(3)

为了便于计算，对该问题区域进行离散剖分。每个边分为N份，其等分间距为Δx=Δy=3/N，于是整个问题区域形成了(N+1)2个节点，其中待求场点为区域中心的(N-1)2个点。

若以场量的下标i和j分别表示x和y方向上的位置指标，则本例的差分分析图示如图1所示。

图1 差分分析图示

将待求场点代到式(3)中的差分方程中，可以进一步得到如下方程组：

φi+1,j-2φi,j+φi-1,j+φi,j+1-2φi,j+φi,j-1=0, (i,j=1,2,3…,N+1)

(4)

值得指出的是，上面(N-1)2个方程中有4(N-1)个量通过边界条件是已知的。通过对方程组中待求场量各项的合并，并将确定场量移到各个方程等号的右端，则可以得到如下矩阵代数方程：

AX=B

(5)

其中，X为待求场量组成的列向量，A为确定的对称系数矩阵，B为确定场量组成的列向量。通过对该方程的求解就可以得到待求场量X=A-1B。

3.3 途径2—矩量法

(6)

其中{(x,y)∂D}，待求的未知函数是产生边界上电位的电荷线密度ρ(x,y)。将边界剖分成N个小段，每段ln长为2b，b=2·3/N。采用脉冲函数

(7)

作为分域基函数，将待求电荷线密度函数展开，于是有

(8)

从上式可以看到，只要求得系数an则可得到电荷的线密度的分布情况。定义适合于该问题的内积为∫∂Df(x,y)g(x,y)dl。将前面电荷线密度的展开式代入上式，并且取检验函数为：wm=δ(x-xm)δ(y-ym)，其中，(xm,ym)为每段 的中点，则得相应矩阵代数方程：

[lm,n][an]=[gm]

(9)

其中

gm=∫∂Dδ(x-xm)δ(y-ym)Vdl

通过对于上面矩阵代数方程的求解，就可以得到电荷线密度分布函数的系数[an]=[lm,n]-1[gm]。图2给出了分析中的矩量离散形式。

在此基础上，可以进一步得到待求场点的静电位：

(10)

图2 矩量分析图示

3.4 途径3—有限元

通过有限元方法也可对本问题进行分析。有限元方法的实质是建立与问题静电能有关的泛函，并分析其变分。对于本文问题，可以建立其所对应的泛函为

(11)

其中，D为整个问题区域。在具体分析时往往要借助化整为零的技巧，即将总的能量分析转换为在一个三角网格上的分析，即H=ΣHn。对全部三角网格及节点编号，其规则如下：①将所有网格按照从1到2N2编号；②将所有节点从1编号到(N+1)2，为全局编号；③对每个网格的节点从l1、2l、3l编号，为局部编号。由于边界上节点的场量是已知的，因此仅需分析待求场量的节点。

图(3)给出了分析中的有限元网格划分规则和局部编号规则。

图3 有限元分析图示

按照图中的规则，在整个网格划分中，分为两类：上三角网格和下三角网格，且所有网格取向与图中所示临近网格去向一致。网格的划分依据先按x向增大，再y向递增的逐次递增编号。通过离散处理，将问题区域划分为2N2个等腰直角网格，进而形成了(N+1)2节点。对第 个网格的电位可分别用三个节点上的电位做线性插值：

(12)

同时考虑在分析中，对三角网格的形状函数进行展开

(13)

其中，An=(y2-y3)x1+(y3-y1)x2+(y1-y2)x3。上式中的所有坐标都使用的是局部编号。接下来可以构建[tn]和各个网格所对应的能量：

(14)

由前面分析可知，三角网格分为两类。根据问题特点，这里采用等腰直角网格，因此，上面的局部分析结果也分两类。对于下三角网格有：

而对于上三角网格：

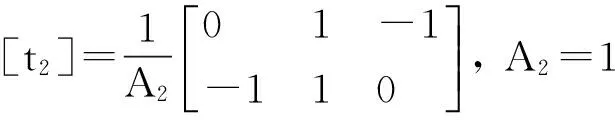
于是进一步的对应可以得到：

(15)

根据变分原理的条件，对剖分所得2N2个局部关系进行整理，则可得到关于(N+1)2个节点的方程组：

(16)

解该代数方程即可确定电位分布。

3.5 结果分析及讨论

为了表明上面三种分析途径的有效性，基于不同途径，分别对前面所建立的统一的二维静电问题模型进行细致分析，得到结果如下图所示：

(a)差分法； (b)矩量法； (c)有限元图4 三种方法分析结果对比

通过对比可以看到，对于同一个问题，三种方法计算结果吻合良好。值得注意的是，通过上面的分析还可以看到，不同方法各有其特点，在实际使用过程中，往往需要和具体问题特点相结合，才能更为高效的发挥其自身优势。在本文问题模型的分析中，通过具体分析过程可以知道，有限差分法较之其它两种相对较优。另外，数值方法存在一定的误差取舍。通常，当减小剖分间距的尺寸或增大离散网格数量时，可以得到更为细致的场分布特性。通过以上对比可以感受到，在实际问题分析中可以采用多种灵活的途径，具体路径的选择则需要根据实际条件合理选择。

4 结语

大学本科研究型教学实际中，从基本知识框架着眼，通过典型问题入手，把不同知识进行对比、联系将对学生的相关专业学习具有重要意义。

在电磁相关学科本科教学实践中，因涉及较多数理专业知识，使得许多学生出现不能积极拓展思维，将多种知识形成联系的问题。对此，本文从大处着眼，小处着手，以电磁专业本科教学实践为研究背景，通过典型问题研究，探索教学活动中问题分析、多样性解决问题及相关基本概念、基本原理、基本方法(三基)的重要作用，讨论问题处理思想的拓展。

由聚拢到发散，再由发散到聚拢……这种思想的启发对于教学非常重要，为了更好地启发多数学生能够更为有效的从多角度来思考电磁知识与计算知识的相互关系，一题多解是一种有效的方法[7]。

[1] J. A. Stratton, Electromagnetic Theory[M]. New York: McGraw-Hill, 1941

[2] 牛中奇. 电磁场理论基础[M]. 北京: 电子工业出版社, 2001

[3] 路宏敏, 朱满座, 赵永久. 电磁场与电磁波[M]. 北京: 科学出版社, 2006

[4] 潘懋元, 王琪. 从高等教育分类看我国特色型大学发展[J]. 北京: 中国高等教育, 2010. 5: 17-19(谭康伯等文)

[5] 邬大光, 赵婷婷, 李枭鹰, 梁燕玲, 李国强. 高等教育强国的内涵、本质与基本特征[J]. 北京: 中国高教研究, 2010. 1: 4-10

[6] 陆国栋. 关于大学教学中若干要素的思考[J]. 北京: 中国大学教学, 2009. 11: 11-13

[7] 梁昌洪. 科学随想录[M]. 西安: 陕西人民教育出版社, 2012

Inspiration from the Analysis of the Simple Electromagnetic Problem

TAN Kang-bo, LU Hong-min, SU Tao

(SchoolofElectricEngineering,XidianUniversity,Xi'an710071,China)

Based on the practical practices in the teaching mode of researching to the juniors and seniors at the electromagnetic related specialties, the basic concepts, the basic principles, and the basic methods are focused and investigated. With the assistance of simple statistic electric problem in electromagnetics, three typical numerical methods, that is differential method, method of moment, and finite element method, are investigated on the basis of the above consideration. Through drawing inferences, the diversity of the problem solving is inspired in the teaching mode of researching.

electromagnetic; statistic field; numerical methods

2016-09-06;

2017-02-08

陕西省精品资源共享课程项目(201522)、陕西省专业综合改革试点项目(201409)

谭康伯(1981-)，男，博士，副教授，主要从事电磁兼容、天线与微波工程教学与研究等工作，E-mail：kbtan@mail.xidian.edu.cn

G420，G642.0，O441，TN802

A

1008-0686(2017)04-0105-05