基于佳点集的蝙蝠定位算法在WSN中应用*

谢国民,干毅军,丁会巧

(1.辽宁工程技术大学电气工程与控制工程学院,辽宁 葫芦岛 125105;2.乌鲁木齐供电公司,乌鲁木齐 830000)

基于佳点集的蝙蝠定位算法在WSN中应用*

谢国民1*,干毅军1,丁会巧2

(1.辽宁工程技术大学电气工程与控制工程学院,辽宁 葫芦岛 125105;2.乌鲁木齐供电公司,乌鲁木齐 830000)

针对无线传感器网络(WSN)节点的定位误差较大的的问题,提出一种新的基于佳点集的蝙蝠定位算法。在改进的算法中,采用基于佳点集的方法对蝙蝠种群个体进行初始化优化,有效提高种群多样性,避免算法过早陷入局部最优;引入部落机制及自适应更新方式,可有效避免局部最优解的吸引,加快收敛速度;通过重构部落利用pareto分级有效避免个别优秀个体被淘汰,增强了泛化能力,提高算法精度。通过MATLAB模拟仿真平台仿真实验表明,改进后的算法具有较好的收敛性和良好的寻优性能,降低测距误差对定位的影响,提高节点的定位精度。算法系统实现条件简单、精度高,具有较高的实际应用价值。

蝙蝠算法;佳点集;部落机制;WSN

无线传感器网络WSN(WirelessSensor Network)是由许多传感器节点组成采用无线通信方式连接的一个多跳自组织的网络系统,具备检测感知、采集和处理信息的功能[1]。在无线传感器网络的应用中,实时获取事件发生位置或节点信息是WSN的基本功能之一,因此节点定位是无线传感器网络中的一个重要问题,引入位置信息,才能使得无线传感器网络的许多检测数据变得更有意义[2]。

针对WSN定位方法,国内外学者进行大量研究,定位算法分为两类:节点自身的定位和目标节点的定位,其中节点自身定位算法分为基于测距技术的定位算法和无需测距的定位算法。基于测距技术的定位算法通过测量节点间的距离或者角度信息,使用三边测量法、三角测量法或最大似然估计法来计算节点位置,包括RSSI(Received Signal Strength Indicator)定位[3]、TOA(Time of Arrival)定位[4]、TDOA(Time Difference On Arrival)定位[5]和AOA(Angle of Arrival)定位[6],算法定位精度较高,但因额外的硬件设置,成本大而使其使用受限;无需测距的定位算法有质心定位、凸规划定位[7]、DV-HOP(Distance Vector HOP)定位、Amorphous定位、MDS-MAP定位[8]和APIT(Approximate PIT Test)定位[9],此类定位算法是通过锚节点的信息和网络连通度来估计节点位置,无需额外硬件支持,算法简单,成本低,但存在定位精度不高等缺点。随着无线传感器技术的发展,已将无线传感器的节点定位问题转换为约束优化问题,通过智能算法对节点进一步优化以提高定位精度[10-13]。蝙蝠算法BA(Bat Algorithm)具有模型简单,寻优能力强等优点可用以解决WSN定位问题;但基本蝙蝠算法存在易早收敛、后期收敛速度慢、局部搜索能力弱等缺点。

针对蝙蝠算法的缺点,本文提出一种基于佳点集的自适应蝙蝠算法GBA(Good-Point Bat Algorithm)用于WSN系统中的节点定位,采用佳点集方法对WSN系统中的节点初始化进行优化,使其均匀分布于解空间,保持种群的多样性;通过GBA算法全局搜索解空间,利用自适应搜索算子的位置更新方法,加快算法的收敛速度,提高蝙蝠算法的全局搜索能力。

图1 无线传感器网络典型的体系结构

1 无线传感器网络体系

无线传感器网络典型的体系结构如图1所示。定位网络是由随机部署的待定位节点和参考锚节点组成。锚节点通过向其他节点广播自身的位置信息,为其他节点确定位置提供信息。在传感器网络中除了知道自身位置信息的锚节点外就是待定位节点。待定位节点通过锚节点提供的信息和定位算法计算出自身的位置。定位算法就是以多节点构成的传感器网络为硬件基础,通过相应的软件设计实现的。精度高、容错能力强定位算法将极大提高定位节点的定位精度。将基于佳点集的自适应蝙蝠算法应用于定位系统,将有效的提高定位节点的定位精度及定位速度。

2 基于佳点集的蝙蝠定位算法

2.1 基于佳点集蝙蝠定位算法方法论

选取适应度函数f(xi)来体现WSN定位系统的精度,f(xi)函数值大小在蝙蝠算法中代表种群个体位置的优劣,适应度函数与种群个体位置构成如式(1)所示关系:

(1)

蝙蝠算法通过超声波搜索,利用回声定位的原理进行猎物搜索,蝙蝠种群在初始化时个体应尽可能的均匀分布在整个搜索空间中[14],采用佳点集的蝙蝠算法在整个搜索空间内进行均匀搜索能以较快的收敛速度快速逼近最优解。

对于搜索空间中的初始种群,既不能粗略的随机产生,又不能遍历所有的状况,通过数论中的佳点集原理设计出均匀分布于搜索空间的初始种群,以保持种群良好的多样性。在佳点集的定义[15-18]中,设GD是D维欧式空间中的单位立方体,如果rGD,形为

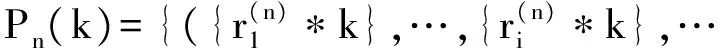
(2)

其偏差φ(n)=C(r,ε)n-1+ε,则称Pn(k)为佳点集,r为佳点,其中C(r,ε)是只与r、ε(ε>0)有关的常数。取rk={2cos(2πr/p)},1≤k≤n,p是满足(p-D/2)≥D的最小素数,或rk={exp(k)},1≤k≤n,{a}表示a的小数部分。理论[19]上已证明,用n个佳点构成的加权和比采用任何其他n个点所得到的误差都要小。

fi=fmin+β(fmax+fmin)

(3)

(4)

(5)

式中:fmin和fmax是声音频率的最小值和最大值;β[0,1]是一个服从均匀分布的随机向量,x*表示当前全局最优解。

种群个体在不断更新,蝙蝠个体在靠近猎物时,音量逐渐降低,脉冲频率逐渐增高,直到蝙蝠个体i搜索到一只猎物时Ai=0,此时停止发音,其更新公式如下

(6)

(7)

为了提高蝙蝠算法的收敛能力以及避免陷入局部最优解,将部落机制引入蝙蝠算法中,将蝙蝠族群划分为规模相同的部落,如图2所示。

由图2可以看出,该划分策略分为两部分:首先是由n个个体组成的部落内部寻出局部最优解转移并记录;其次是将转移的局部最优解组成新部落寻找全局最优解。充分利用蝙蝠算法的局部搜索能力和全局信息交换能力可以使得全局最优信息能在种群群体中有效传递,提高了算法的收敛效率。

图2 部落机制结构

为避免盲目搜索,定义个体适应度调节项和自适应搜索算子,根据个体在每个目标上的适应度值自适应调整搜索范围,如下式所示:

(8)

(9)

(10)

将一次迭代后得到的种群,利用pareto,对相同pareto等级相同的个体按照个体优劣比较原则进行拥挤距离排序,并取出q个个体,更新种群w。

重新构造种群后,采用式(11)计算个体未更新次数:

(11)

2.2 基于佳点集蝙蝠定位算法流程

基于佳点集的蝙蝠定位算法主要思想是通过蝙蝠种群初始化使种群均匀分布,然后将均匀分布的种群个体划分为若干部落寻找出各部落的最优个体,将部落最优个体组成新部落寻出最优个体,循环反复,寻找出最优个体。主要工作步骤如下:

Step 1 定义适应度函数f(xi),xi=(x1,x2,…,xd)T,其中d为维数,x为蝙蝠个体的位置,f(xi)的最优解就是蝙蝠个体搜索到猎物的位置;

Step 2 采用佳点集的方法随机构成蝙蝠种群w,每个个体为xi=(i=1,2,…,n)(n为种群数量),并平均划分为n个部落;定义蝙蝠个体所在位置xi和飞行速度vi以及频率fi;定义蝙蝠发出的音量Ai、脉冲发生率ri、迭代次数。为了方便计算,音量和脉冲频率都设为常数0.5。

Setp 4 选择初始种群w中优秀的个体执行更新并记录新个体,采用轮盘赌方式执行Q次选择,按照个体优劣比较规则每次选出一个pareto等级较低、拥挤距离较大的优秀个体执行式(9),产生的新个体由式(10)记录进入外部集合w′。

Setp 5 按照3.4策略重新构造种群w,并按式(11)记录未被更新次数triali。

Setp 6 淘汰w中多次未被更新的个体。选择triali值最大且pareto等级大于1的个体xi,随机产生新的个体代替xi。

Setp 7 判断是否达到算法结束条件,若达到,输出最优解,否则转到Setp 3。

为了配合改进后的更新策略,Setp 6调整了个体淘汰机制,直接选择pareto等级不为1的最久未被更新的个体做更新,这样算法在选择被淘汰个体时避开了pareto等级为1的个体,防止优秀个体被淘汰。

3 基于佳点集的蝙蝠定位算法试验和分析

3.1 基于佳点集的蝙蝠定位算法试验参数设置

为了验证GBA算法在传感器定位方面的性能,利用MATLAB2014进行仿真测试,已知300个节点(包括锚节点和未知节点),锚节点比例为10%,节点通信半径为30m,随机分布于100m×100m的区域内。将GBA的定位性能与未改进的蝙蝠算法(BA)、粒子群优化算法(PSO)进行对比实验,并采用平均定位误差(error)作为定位结果评价标准,error定义为:

(12)

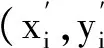
在改进的蝙蝠算法中,初始响度和初始飞行速度在区间[0,1]内随机产生,初始频率均为0,其他参数如表1所示。

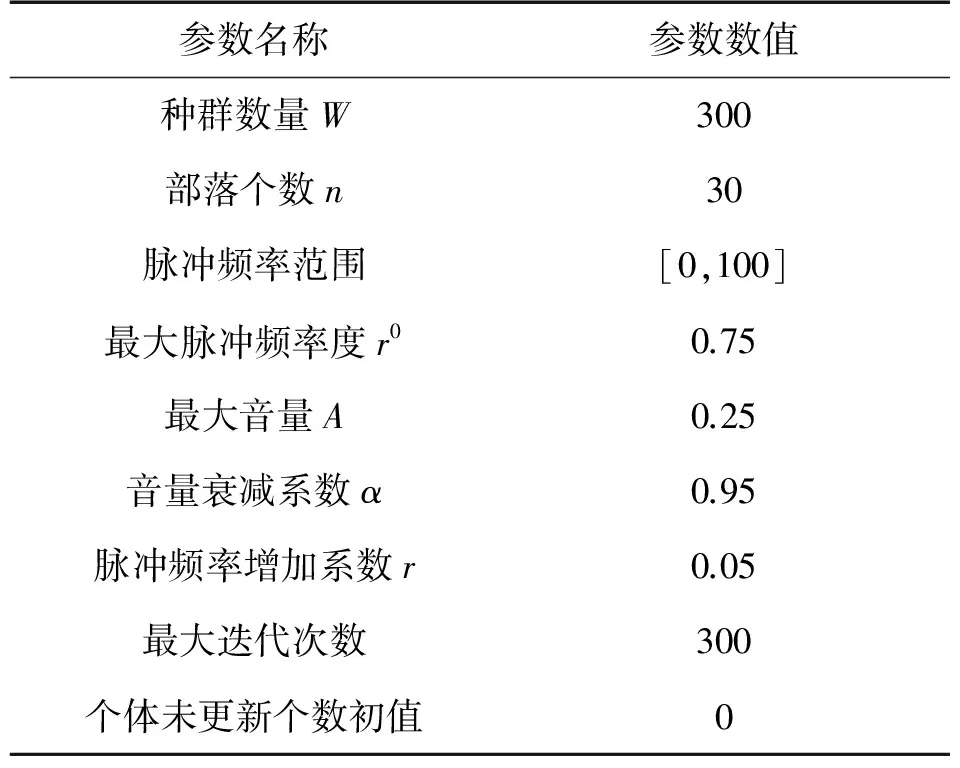
表1 蝙蝠参数

3.2 基于佳点集的蝙蝠定位算法试验结果分析

3.2.1 随机与佳点集的初始化比较

图3分别给出了随机分布点法和佳点集布点法两种不同方法构造的含有300个二维点的初始种群分布图。从图中可以看出,采用佳点集方法产生的初始种群分布比随机方法产生的初始种群要均匀,有着较好的多样性,算法表现较稳定且始终保持初始种群良好的多样性,从而避免出现早熟现象,最终收敛到全局最优。

图3 种群初始化

3.2.2 GBA、BA与PSO的收敛速度对比

GBA、BA以及PSO在定位过程中适应度值的变化曲线如图4所示,从图4可以看出,相对于PSO算法以及BA算法,GBA的求解速度明显加快,只需经过43次迭代就找到了适应度最大值,即寻找到未知节点的最优解,而未经改进的BA算法和PSO算法则分别经历了70次和130次才寻找到最优解。对比结果表明,改进的BA算法在传感器的定位过程中不仅有效降低了传感器的定位误差,而且加快了定位问题的求解速度,是一种速度快、精度高的传感器定位算法。

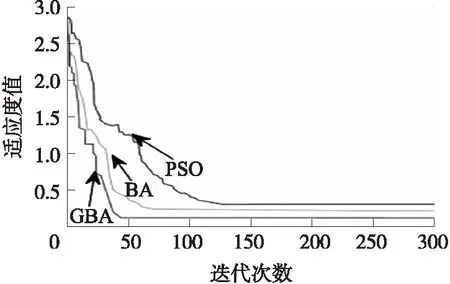
图4 GBA、BA及PSO收敛速度对比

3.2.3 不同的测距误差的定位性能比较

在传感器节点的定位算法中,测距误差对未知节点的位置信息有着直接的影响。不同的测距误差下GBA、BA以及PSO的平均定位误差试验数据如表2所示。从表2可知,在测距误差为8%时,GBA算法的定位误差趋于稳定,为12.1%;BA算法的定位误差为26.1%,是GBA的2.16倍;PSO算法的定位误差是58.44%,是GBA算法的4.83倍。且随着测距误差的增大,BA算法和GBA算法的定位误差也随之增大,其变化趋势如图5所示。相对于PSO算法和BA算法,GBA算法的定位误差更小,可以有效的抑制节点测距误差的累计,一定程度上提高了传感器节点的定位精度。同时,GBA算法相对于BA算法有着更强的局部搜索能力和信息交换能力。

表2 不同测距误差下的定位误差试验数据

图5 测距误差变化的定位性能比较

3.2.4 不同锚节点数量的定位性能比较

不同数量锚节点的情况下,GBA、BA、PSO的平均定位误差变化曲线如图6所示。从图6可知,随着锚节点数的不断增加,GBA、BA及PSO的定位性能越来越好,平均定位误差越来越小。当具有相同的锚节点时,GBA算法的定位误差最小,PSO算法的定位误差最大。增加相同数量锚节点时,GBA、BA、PSO算法的定位误差量平均减少5.34%、4.98%、5.99%。虽然PSO算法随着锚节点数的增加,定位误差减小速度较快,易获得较高的定位精度,但相应的锚节点成本也随之增加。而改进的蝙蝠算法(GBA)在较小的锚节点密度下即能获得较高的节点定位精度,锚节点相关成本较低。可见相对于另外两种算法,在相同的定位精度的条件下,GBA降低了节点定位成本,具有更好的定位价值。

图6 不同数量锚节点时的定位性能对比

4 结论

为了改进蝙蝠算法在无线传感器应用中的定位性能,本文提出了一种基于佳点集的自适应蝙蝠定位算法,其优越性体现如下:

利用佳点集对传统蝙蝠算法进行种群初始化,使得种群搜索节点更均匀,保持了种群良好的多样性;采用部落机制避免了最优解陷入局部最优,加快了算法的收敛速度,提高了定位精度;引入了改进的更新策略,使得在较小锚节点密度下,即获得较高的节点定位精度,同时还降低了锚节点相关成本。

通过对比仿真实验分析,改进后的蝙蝠算法具有更快的收敛速度和良好的收敛性能。降低了测距误差对定位的影响,提高了传感器节点的定位精度,为无线传感器节点定位提供了一种较好的解决方案。

[1]Liu Q,Huang S P. Deployment Strategy of Wireless Seneor Networks for Internet of Things[J]. China Communication 2011,8(8):111-120.

[2]Hang J,Xu H H,Duong T Q,et al. Localization Algorithms of Wireless Sensor Networks:A Survey[J]. Telecommunication Systems,2011.4(52):1-18.

[3]Qiao G,Li X,Zeng J.Design and Implement of RSSI Positioning System on TinyOS Platform[J]. Electronic Science and Technology,2013,26(2):90-93.

[4]Monir Vaghefi S Y,Vaghefi R M. A Novel Multilayer Neural Network Model for TOA-Based Localization in Wireless Sensor Networks[C]//The 2011 International Joint Conference on Neural Networks(IJCNN). IEEE,2011:3079-3084.

[5]Kaune R,Horst J,Koch W. Accuracy Analysis for TDOA Localization in Sensor Networks[C]//2011 Proceedings of the 14th International Conference on InformationFusion(FUSION). IEEE,2011:1-8.

[6]Jiang J R,Lin C M,Lin F Y,et al. ALRD:AOA Localization with RSSI Differences of Directional Antennas forwireless Sensor Networks[C]//2012 International Conference on Information Society(i-Society). IEEE,2012:304-309.

[7]Doherty L,El Ghaoui L.Convex Position Estimationin Wireless Sensor Networks[C]//INFOCOM 2001. Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings IEEE.IEEE,2001,3:1655-1663.

[8]Buja A,Swayne D F,Littman M,et al. XGvis:Interactive Data Visualization with Multidimensional Scaling[J]. Journal of Computational and Graphical Statistics,2004(5):21-53.

[9]彭宇,王丹. 无线传感器网络定位技术综述[J]. 电子测量与仪器学报,2011,5(25):389-399.

[10]李牧东,熊摇伟,梁摇青. 基于人工蜂群改进算法的无线传感器网络定位算法[J]. 传感技术学报.2013,26(2):241-245.

[11]曹欲晓,严奎,徐金宝. 一种最优锚节点集合上的两重粒子群优化DV-HOP定位算法[J]. 传感技术学报,2015,28(3):424-430.

[12]石欣,印爱民,张琦. 基于K最近邻分类的无线传感器网络定位算法[J]. 仪器仪表学报,2014,10(35):2238-2247.

[13]张震,闫连山,刘江涛,等. 基于DV-hop的无线传感器网络定位算法研究[J]. 传感技术学报,2011,24(10):1469-1472.

[14]黄光球,赵魏娟,陆秋琴. 求解大规模优化问题的可全局收敛蝙蝠算法[J]. 计算机应用研究,2013,30(5):1323-1328.

[15]李志俊,程家心. 免疫佳点集遗传算法[J]. 计算机工程与应用,2007,43(28):37-40.

[16]肖赤心,蔡自心,王勇,等. 一种基于佳点集原理的约束优化进化算法[J]. 控制与决策,2009,24(2):249-253.

[17]梁昔明,陈富,龙文. 基于动态随机搜索和佳点集构造的改进粒子群优化算法[J]. 计算机应用,2011,31(10):2796-2799.

[18]刘香品,宣士斌,刘峰. 引入佳点集和猴群翻过程的人工蜂群算法[J]. 模式识别与人工智能,2015,28(1):80-89.

[19]龙文,梁昔明,徐松金,等. 聚类佳点集交叉的约束优化混合进化算法[J]. 计算机研究与发展,2012,49(8):1753-1761.

A Positioning Algorithm Based on Bat Algorithm andGood-Point Setsin the Application of WSN*

XIEGuomin1*,GANYijun1,DINGHuiqiao2

(1.College of Electrical and Control Engineering,Liaoning Technical University,Huludao Liaoning 125105,China;2.Urumqi Power Supply Company,Xinjiang Autonomous Region,Urumqi 83000,China)

In order to solve the problem that node localization error in wireless sensor network(WSN)is large,this paper proposes a new bat positioning algorithm based on good point set. In the improved algorithm,the bat population individual is optimized by the good point set method,which can effectively improve the population diversity and prevent the algorithm from falling into the local optimum;The method by introducing tribal mechanism and adaptive updating can effectively avoid attracting the local optimal solution and expedite the convergence speed;Reconstructing the tribe by pareto classification can avoid eliminating the isolated outstanding individuals,enhance the generalization ability and improve the algorithm precision. By the simulation experiments on MATLAB,the results show that the improved algorithm has good convergence and searching performance,also reduces the influence of ranging error on positioning,and improves the nodes positioning accuracy. The algorithm is simple in implementation,high in precision and high in practical value.

bat algorithm;good-point set;tribal mechanism;WSN

谢国民(1969-)，男，辽宁阜新人，博士，副教授，研究生导师。主要从事电气工程和智能检测及电气控制方面的研究工作，lngdxgm@163．com；干毅军(1992-)，男，湖北武穴人，辽宁工程技术大学电气与控制工程学院硕士研究生，主要研究方向为智能检测与电气控制，770827125@qq．com； 丁会巧(1991-)，女，河北沧州人，硕士研究生，主要研究指那个检测与电气控制。现就职于国家电网乌鲁木齐供电公司，313134949@qq．com。

项目来源:国家自然科学基金项目(51274118);辽宁省重点实验室项目(LJZS003);辽宁省教育厅基金项目(UPRP20140464)

2017-01-06 修改日期:2017-03-10

TP391;TP212

A

1004-1699(2017)08-1252-06

C:7230

10.3969/j.issn.1004-1699.2017.08.021