一种基于自适应代表节点选择的WSN数据收集方法*
谢成阳,牛玉刚*,陈 蓓
(1.华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237;2.上海电气集团股份有限公司中央研究院,上海 200070)
一种基于自适应代表节点选择的WSN数据收集方法*
谢成阳1,牛玉刚1*,陈 蓓2
(1.华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237;2.上海电气集团股份有限公司中央研究院,上海 200070)
采用压缩感知的无线传感网络数据收集方法要求每个节点都参与数据收集,会造成很大的能量浪费。本文提出了一种基于自适应代表节点选择的WSN数据收集方法,在保证压缩感知数据重构精度的同时,减少参与数据收集的节点数。首先,采用主成分分析和混合压缩感知相结合的办法设计稀疏基;然后,通过分析稀疏基的框架势FP(Frame Potential)设计压缩感知的稀疏观测矩阵,从而选择代表节点,以减少参与数据收集的节点数目;最后,根据Sink处数据重构精度,自适应调整稀疏观测矩阵以用作下一时刻数据收集,从而保证数据收集的重构精度。仿真结果表明,该方法有效的降低了网络能耗和数据传输量,同时还保证了每个时刻数据重构的精度。
无线传感网络;代表节点选择;压缩感知;主成分分析;框架势
无线传感网络WSN(Wireless Sensor Network)在军事、环境、医疗和工业等方面都有着广泛的运用[1]。然而,由于传感器尺寸和安放环境的约束,造成其电池电量有限且很难得到更换,所以网络能耗是WSN设计时必须考虑的主要问题。由于压缩感知CS(Compressed Sensing)技术可以有效的减少网络数据发送量,节约网络数据收集的能量,因此,CS技术受到了许多学者的关注[2-3]。然而,直接采用CS与WSN数据收集相结合的方法要求网络中所有节点都参与CS数据收集,这仍然会造成很大的能量消耗。因此,人们提出了很多基于CS的改进方法。文献[4]提出了CS技术的改进方法混合压缩感知(Hybrid-CS),当节点收到的数据包数大于一定值时,节点才进行数据压缩,减少了网络发送的数据包数。文献[5]将Hybrid-CS与数据收集树的构建过程相结合,根据节点的剩余能量,设计出一种长生命周期数据收集方法,有效的提高了网络的生命周期。另一种减少网络能耗的办法是通过优化CS本身的结构,对传统观测矩阵和稀疏基进行改进。文献[6]设计了一种CS观测矩阵,用以减少每一轮参加数据收集的节点数目,并证明其满足CS数据重构的条件。然而,上述方法虽然能减少网络数据量,但整个网络的数据量仍然偏高,并且往往在减少网络数据量的同时,CS数据重构精度会因为观测值信息的减少而降低。
针对此问题,本文提出了一种基于自适应代表节点选择的数据收集ARNS-DG(Adaptive Representative Nodes Selection Data Gathering)方法,主要创新点如下:①运用主成分分析PCA(Principal Component Analysis)对传感器所收集数据进行分析,从而进行CS稀疏基设计,这样每个时刻的稀疏基可随着传感器信号的变化而变化,可为始终选择具有代表性的节点提供条件;②将框架势FP(Frame Potential)性质与PCA相结合,用来分析稀疏基以确定M×N维稀疏观测矩阵,从而确定代表节点。在此稀疏观测矩阵下,只需从N个节点中选择M个具有代表性的节点以参加数据收集,从而减少网络的数据量,并使观测值包含更多的传感器数据信息;③通过代表节点进行数据收集后,根据Sink处的数据重构精度所处范围,自适应调整下一时刻ARNS-DG的稀疏观测矩阵内容,从而保证下一时刻数据重构的精度。
1 基于ARNS-DG的WSN方法
1.1 WSN数据收集模型和CS
考虑由N个节点组成的WSN,所有节点(除Sink外)都同构且统一随机的分布在一片监控区域内。假设每个节点都具有相同的初始能量和传输半径r,WSN中每个节点都有采集信息并将信息发送给Sink节点的能力,且节点所收集信息在时间和空间上具有相关性,距离小于r的两个传感器节点间可相互通信,由于传输距离的限制,大部分节点不能直接将数据发送给Sink节点,而是采用多跳可靠的网络协议将数据传输给Sink节点。
若不采用数据融合的方法,越靠近Sink的节点需要发送和接收的数据越多,消耗能量的速度也越快。基于CS的WSN数据收集中,Sink不需要接收所有节点发送的N个数据包,只需接收M个压缩数据包,然后对此M个数据包进行数据重构。
设所有节点收集的信号为x=(x1,x2,…xN)T,利用各节点收集信号的相关性,若信号x满足:
(1)
式中:稀疏基ψ一般为N×N维正交矩阵,θ为N×1维被稀疏后的信号,其N个元素中只有L个不为零(或此L个元素远大于其他N-L个接近于0的元素),则称信号x在稀疏基ψ下是L阶稀疏,信号x再通过与稀疏基ψ不相关的M×N(其中N>M>L)维观测矩阵φ相乘得到M×1维观测值y:

(2)
当观测矩阵φ满足RIP[7]性质,且矩阵ψ,φ满足:
(3)
时,则可通过解式(4)后得到稀疏信号θ,从而恢复传感器信号x。

(4)
式中:C为常数,μ(φ,ψ)为观测矩阵φ和稀疏基ψ之间的相关程度。
Hybrid-CS是CS数据收集方法的一种改进,它将WSN中的节点分为两种类型,即转发节点和压缩节点。转发节点需要发送其收集的数据并转发子节点发送来的数据;而压缩节点对其本身收集的数据和子节点发送来的数据进行压缩,变为M个数据包。图1为简单链式传输结构中3种不同原理下的数据传输过程。图1中,箭头上的数据代表节点发送的数据包数,带上划线的数据代表经压缩后的数据包数。从图1可知,相比于CS,Hybrid-CS数据收集过程可进一步减少网络数据传输量。
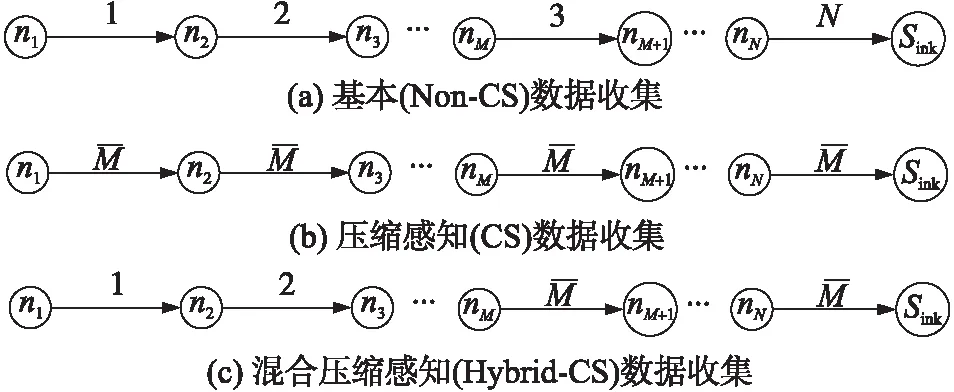
图1 Non-CS(基本)、CS、Hybrid-CS数据收集过程对比
1.2 ARNS-DG方法
基于CS技术的数据收集过程中,由式(2)可知对于第i轮观测值yi和观测值向量y有:
(5)
式中:φ1,φ2,…,φN为观测矩阵φ的N个列向量,φi1,φi2,…,φiN是其第i行的N个元素。由式(5)知,当φi1,φi2,…,φiN中有元素为0时,其对应的节点就不需要参与第i轮的数据收集,而当整个列向量为0向量时,则对应的节点就不用进行数据收集[8]。因此,参与CS数据收集节点的选择过程,实际上就是CS观测矩阵的设计过程。
普通CS中的观测矩阵一般采用高斯随机矩阵[9],其每轮0元素很少,且列向量都不为零向量,则所有节点都须参与CS的数据收集过程,即使是采用Hybrid-CS,其每轮参与数据收集的节点数仍然较多。若要减少参与数据收集的节点数目,则应进一步增加观测矩阵中0元素的数目,或使一部分列向量为零向量,即将观测矩阵变稀疏,相比于大部分元素非零的高斯观测矩阵,由于此类观测矩阵大部分元素为0,则可称其为稀疏观测矩阵。但由于稀疏观测矩阵中0元素较多,若要保证CS数据重构的精度,则一般需要增加稀疏观测矩阵维数M以获得更多观测值,这样又会增加网络能耗。因此,需要考虑一种方法在减少参与数据收集的节点数的同时,又保证CS数据重构的精度。
1.2.1 CS矩阵设计
设有集合χ(k)={x(1),x(2),…x(k)}代表WSN节点从时刻1到时刻k收集的k个N维信号,则信号均值和协方差矩阵为:
(6)
取协方差矩阵的L个最大特征值所对应的单位特征向量,并按对应特征值大小降序排列,即为N×L维正交矩阵U。
PCA是由Karhunen-Loeve理论发展而来的一种方法,其主要原理是用压缩后的M维数据表示原来的N维数据,从而对数据进行降维。根据PCA理论,可将信号x(k)通过L×1维的信号α(k)表示出来,即:
(7)
式中:α(k)的维数根据原信号x(k)变化。
根据PCA这一特点,可将PCA与CS技术相结合[10],联立式(2)与式(7)有:
(8)
则可知新的稀疏基即为U,可通过式(4)类似的方法解式(8),得到α(k)后即可通过式(7)重构出原信号x(k)。由于根据PCA设计的稀疏基可根据传感器信号变化而发生变化,因此,代表节点选择也可随之而变化,从而始终挑选具有强代表性的节点。
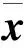
文献[11]证明了此稀疏观测矩阵满足RIP性质。对式(5)运用此观测矩阵,则有:
y=φe1x1+φe2x2+…+φeNxN=(xr1xr2…xrM)T
(9)
式中:r1,r2,…rM代表每轮被选择的节点序号。根据式(9)可知,每轮只有一个节点进行数据收集,M轮观测值只需要从N个节点中选择M个节点进行数据收集即可形成观测值向量y。
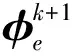
1.2.2 代表节点选择
由于稀疏观测矩阵φe的内容每时刻并不固定,所以需要一种方法来确定每个时刻的φe,即确定ARNS-DG中每个时刻参与数据收集的M个代表节点,文献[10-11]采用一定概率从N个节点中随机的选择M个节点,同时确定稀疏观测矩阵φe,这种方法虽然容易实现,但随机选择的节点可能都集中在一小块区域,使所选节点的信号不能很好的代表整个WSN区域的N个节点收集的信号。
根据1.2节分析可知,若在第k+1时刻用M个节点的信号来得到α(k+1),则应使这M个节点的信号包含尽可能多的节点信息。设代表被选择代表节点序号的集合,矩阵的FP指标可以用来确定传感器节点的放置位置[12],同样,可将FP运用于稀疏基U来确定,从而选择含更多的信息的节点。矩阵U关于集合的FP指标定义如下:
FP(U,
(10)
式中:ui,uj为稀疏基U的第i,j个行向量。根据文献[13]可知,矩阵的FP值越大,其稀疏性越差,所以从N个节点中选择M个节点,就相当于从U中选择M个能让矩阵U的FP最小的行,即去掉N-M让U的FP值最大的行。设被删除节点的序号集合为υ,由前k个时刻采样信号的U(k)确定k+1时刻代表节点序号(k+1)的步骤如下:
输入k时刻稀疏基U(k),选择节点数目M
输出k+1时刻被选择节点序号(k+1)
②υ(k+1)=∅ /*初始化υ(k+1)*/
③υ(k+1)=argmaxi,j∈|
⑥ifi*=argmaxi*∈(k+1)FP(Uk,i*){
⑧υ(k+1)=υ(k+1)∪i*/*更新υ(k+1)*/
}
}
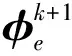
图2为常见树形结构下,经过代表节点选择后的数据收集过程与基本数据收集(Non-CS)、单纯运用CS和Hybrid-CS下的3种数据收集过程的对比,黑色节点即为需要进行数据收集的节点,路径旁的数据代表节点发送的数据包数,带上划线的数据代表经压缩后的数据包数。从图2(d)中可知采用代表节点选择后,只有代表节点需要进行数据收集并将数据发送给Sink,而非代表节点只需要转发数据包即可,因此其网络发送的数据量相对于其他3种方法有明显减少。
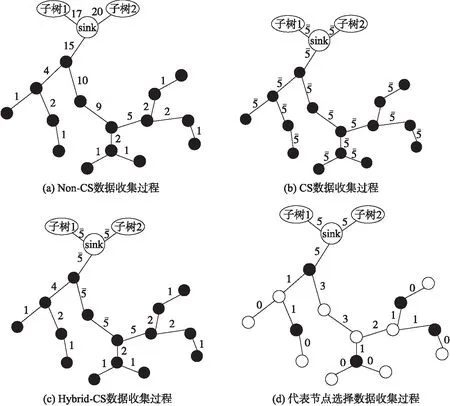
图2 树形结构下4种方法数据收集对比
1.2.3 自适应精度调整
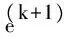
对于问题①,常见的方法是:前k个时刻要求所有节点都直接将信息发送给Sink节点。这种方法虽然简便,但在WSN中传输的数据包较多时,很容易发生丢包,并且这对能量受限的传感器节点也会造成很大的能量消耗。可运用Hybrid-CS进行前k个时刻的数据收集,它可进一步减少网络传输的数据包量,减少节点的能量消耗[14],其重构信号的精度也很高,所以,在前k个时刻可以用Hybird-CS进行数据收集,并利用在Sink处重构后的信号代替前k个时刻的采样信号。
由文献[2]可知,M合适的取值范围为30%N~40%N,当M越大时,获得的观测值数量也就越多,所以对于问题(2),应通过前一时刻数据重构的精度确定下一时刻选择的节点数,即M值,来自适应的调整重构精度。当上一时刻Sink处的数据重构精度过低时,则须增加M值,即增加代表节点数量,以获得更多WSN的信息,此时观测矩阵的维数就需增加;而当上一时刻Sink处的数据重构精度足够高时,则可适当降低M值,即降低观测矩阵维数,以减少代表节点数量。
根据式(9)可知,运用稀疏观测矩阵后,Sink会直接收到被选择代表节点发送的信息,因此在Sink可用指标ε:
(11)
来判断每时刻信号重构的误差,其中,xs为被选择节点发送给Sink的原始数据,xrs为重构后的信号中,对应于被选节点序号的数据。可在Sink处进行数据重构后,判断指标ε是否超过上、下限阀值εmin,εmax来判断下一时刻是否改变M值,并且对于M,还可设置上限Mmax,当M大于Mmax时,则可认为此时ARNS的重构精度过低,应重新开始整个ARNS过程。
1.2.4 网络数据量分析
这里将选择3种数据收集策略,即单纯运用CS和Hybrid-CS以及本方法ARNS-DG,分别计算它们运用在同一WSN下的网络数据量的复杂度,在整个计算过程中,假设每个节点到Sink节点的平均跳数为d,整个网络的节点数为N,3种方法都按相同路由将数据发送给Sink。
对于单独运用CS下的压缩数据收集过程,由于其采用高斯观测矩阵,因此其每行有O(N)个非零元素,并且根据CS的原理可知,每个节点需要向其下一跳节点发送M个压缩数据包,这样,Sink可收到M个投影值以进行信号的重构。因此,单纯运用CS下的网络数据传输量为:
TRSCS=O(MN)
(12)
对于本方法ARNS-DG下的收集过程,由于稀疏观测矩阵的每行仅有一个非零元素,那么整个过程只需要M个代表节点进行压缩数据收集,并且由于采用了代表节点选择,所以节点选择比较均衡,即仍可认为每个代表节点到Sink节点的平均跳数为d。因此,ARNS-DG下的网络传输量为:
TRSARNS-DG=O(Md)
(13)
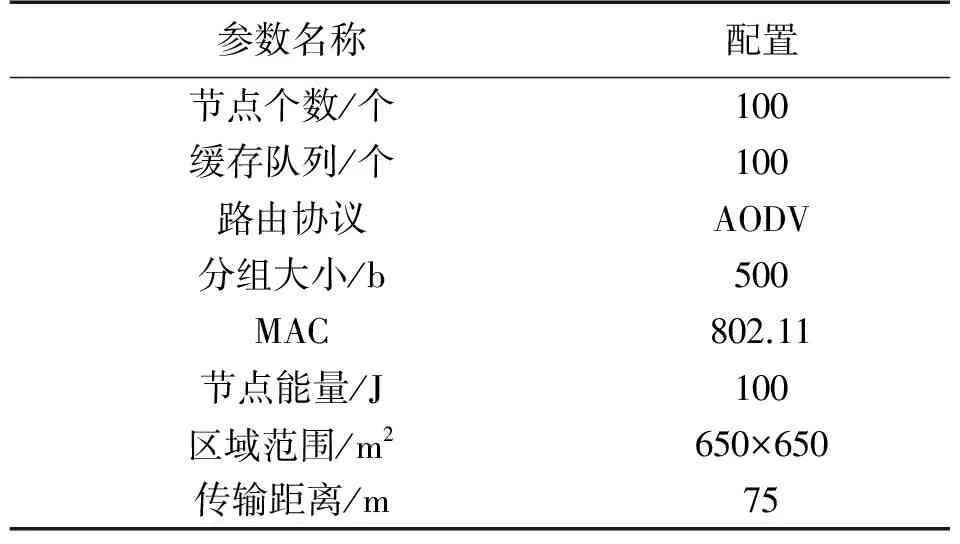
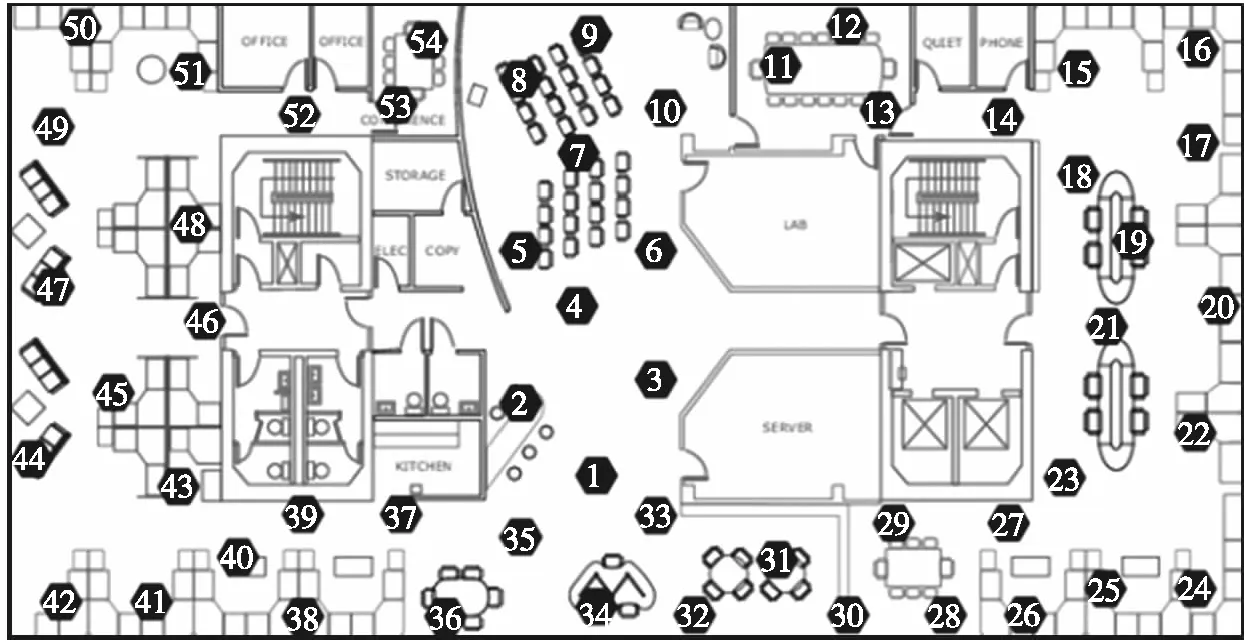
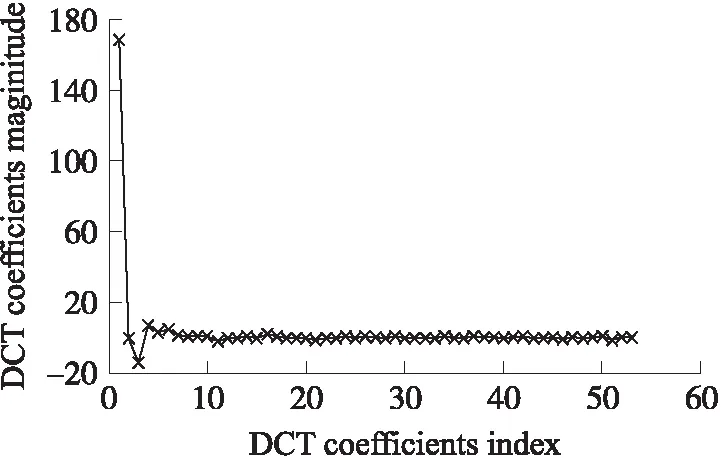
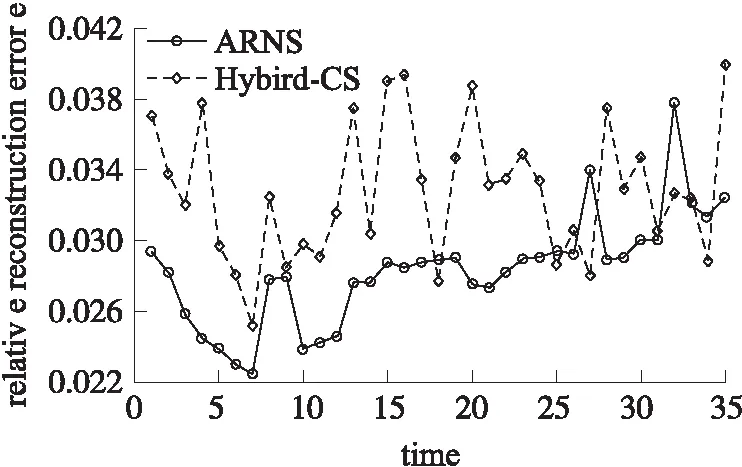
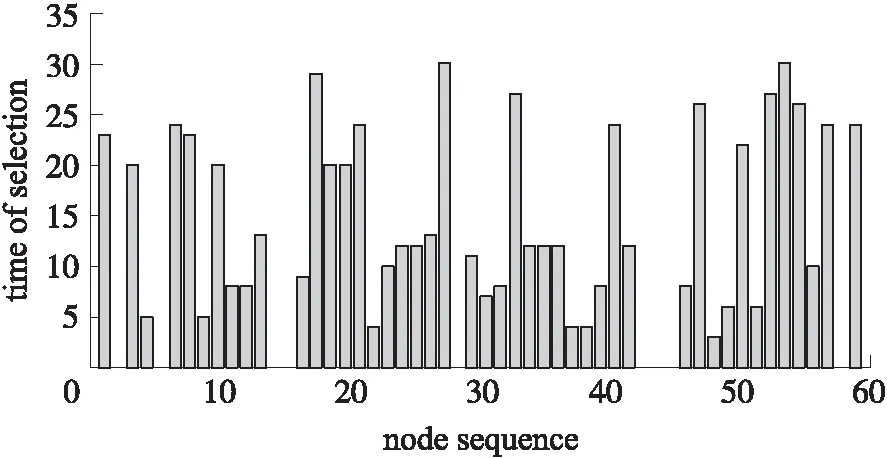
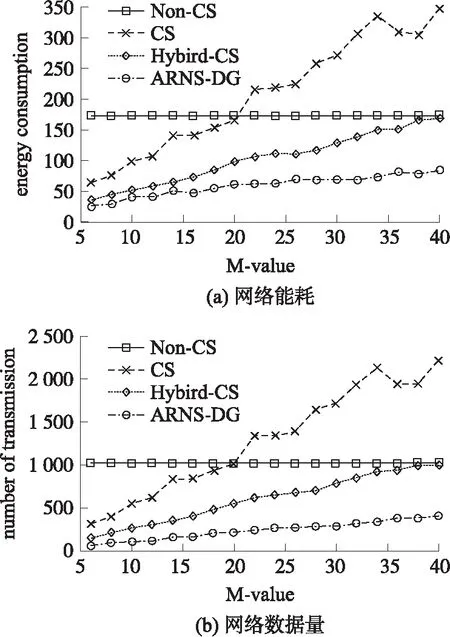
由于平均跳数为d 而对于Hybrid-CS数据收集过程,它将节点分为压缩节点和转发节点,并要求所有N个节点都参加数据收集,则可将其网络数据量分为两部分,即转发节点部分和压缩节点部分。在相同路由下,ARNS-DG中总共只有M个代表节点产生数据,则ARNS-DG下节点发送给下一跳节点的包数最多为M,即ARNS-DG的数据量只相当于Hybrid-CS转发节点数据量的一部分,则可知ARNS-DG的数据量是优于Hybrid-CS的。而根据2.1节中的分析可知,Hybird-CS下的网络数据量是优于单纯运用CS的,因此有: TRSARNS-DG (14) 1.3ARNS-DG方法过程 ARNS-DG方法的实施过程如图3所示,整个过程分为三大部分。 图3 ARNS-DG方法过程 第3部分通过在k时刻后,每个时刻的指标ε和M值的范围,对M值保持不变、增加、减少间隔值Δ或重新开始ARNS方法,来达到自适应精度控制的目的。 与传统的数据压缩方法相比[16],由于ARNS-DG方法采用的稀疏观测矩阵非零元素的值均为1,所以每个代表节点直接将其采样数据发送给Sink即可(采样数据与1相乘仍然为原数据),即ARNS-DG方法在每个节点内不须进行数据压缩的计算,因此其降低了在采样端发生计算错误的可能性,并节约了数据传输时间。 本文的仿真实验分为两个部分,分别为Sink处重构精度仿真和网络能耗及数据量仿真。第1部分采用Intel Berkeley lab[17]的实验数据,运用MATLAB进行重构精度仿真。第2部分选择网络仿真软件NS2进行仿真。 仿真实验过程中主要参数设置如表1、表2所示,并用式(15)中的相对重构误差e来衡量数据重构的精度。式(15)中的衡量指标和式(11)类似,但式(15)中的e是在知道真实数据的情况下,运用实际信号与所提方法重构信号来求相对误差e。 e=‖x-xr‖2/‖x‖2 (15) 表2 NS2仿真参数设置 2.1 重构精度仿真 对WSN使用CS的前提是传感器所收集的信号是可稀疏的,所以需要对信号的可稀疏性进行验证。 如图4所示的WSN中,54个节点均匀的分布在一个实验室里。其中的每一个传感器节点对房间内的温度、湿度和光照水平进行超过一个月的测量。 图4 Intel Berkeley lab WSN 节点分布图 由于实验中的数据有一部分发生了丢包,所以应选择具有连续数据的节点进行稀疏性实验,其中53号节点由于收集的数据有一大部分缺少,所以仿真实验中去掉了53号节点的数据。 图5为全部53个节点前8个时刻的实际温度采样信号经过离散余弦变换DCT(Discrete Cosine Transform)后的稀疏系数均值,从图5中可知,前8个时刻的实际温度采样信号经过DCT后的均值系数大部分都变为0,即信号在DCT下是可稀疏的。同理,其他时刻的温度数据也具有同样的可稀疏性,所以对于ARNS的前8个时刻的采样信号,可采用Hybrid-CS进行收集并重构后的信号进行代替,且可运用DCT域下的矩阵作为前8个时刻Hybrid-CS的稀疏基。 从稀疏性验证可知,可将Hybrid-CS运用于前8个时刻节点的数据收集,则可从第9个时刻开始将ARNS运用到WSN的数据收集过程中。图6是从第9个时刻开始仍采用Hybrid-CS和采用ARNS后的数据相对重构误差e对比,其中,重构算法采用CoSaMP。 图5 温度信号DCT系数幅度均值 图6 数据重构相对误差对比 图6中共有35个时刻的数据重构相对误差,从图6可以看出,Hybrid-CS的下误差e在0.035左右波动,且波动幅度较大;ARNS的误差e在0.03左右波动,且ARNS的自适应精度调整起了明显的作用,在27、32时刻自适应调整M值后精度有了明显回升,而在其他时刻,误差e的波动较小。 图7是运用自适应代表节点选择后,这35个时刻的采样中每个节点被选中的次数,其中53号节点由于收集的数据有一大部分缺少,所以并未统计其被选择次数。 图7 节点选择次数 结合图4和图7可看出,被选择次数多的节点大部分都很具有代表性,并且这35个时刻的数据收集过程中,大部分节点都有被选择,这说明ARNS选择的代表节点基本上可以代表WSN中所有节点的信息。 2.2 网络数据量及能耗仿真 从2.1节仿真可知,ARNS可保证数据重构的精度,并自适应的调整M值,从而调整数据重构的精度。在确定ARNS可以确保数据重构的精度后,还需要验证其运用在一定规模WSN时,网络能耗及数据量的变化情况,此部分运用NS2进行仿真。 整个仿真中设置了100个节点均匀的分布在650 m×650 m的监控环境中,节点的通信范围设为75 m,Sink位于整个监控区域的右上角,图8为Non-CS、CS、Hybrid-CS以及ARNS-DG下网络能耗及网络数据量,其中CS、Hybrid-CS的观测矩阵采用高斯随机矩阵,有小部分元素为0,图中横坐标均为M值。 图8 网络数据发送量及能耗 由图8可知,除Non-CS外,网络数据发送量和网络能耗都随着M值的增加而变大,这是由于随着M值增大,所需的观测值数量也增加,网络接收和发送的包数也变多。而在4种方法的对比中,ARNS-DG下WSN发送的数据包数和网络能耗在不同M值下均最少。所以应尽可能采用ARNS进行数据收集。而当M值大于20时,CS的能耗和数据发送量比Non-CS还大,因此可见,并不适合将CS直接运用到WSN中。而在Hybrid-CS中,当M值大于40时,其数据发送量和能耗基本与Non-CS持平,这是因为在仿真网络中发送包数超过40的节点很少,因此当M值大于40时,Hybrid-CS的效果基本相当于Non-CS,而当M值等于35时,Hybrid-CS可以节约一部分网络能耗,且在此时的数据重构精度也能满足要求,这也是为什么3.1中取M=35%N=18进行前8个时刻Hybird-CS数据收集的原因。 从以上分析可知,整个ARNS-DG的过程中,前8个时刻采用Hybrid-CS获取采样信号,而在之后采用ARNS-DG,并通过自适应调整稀疏观测矩阵来控制精度是非常合理的,这样既可以减少网络能耗和数据量,又能保证数据重构的精度。 本文提出一种基于ARNS的数据收集方法。通过ARNS-DG来减少网络数据量和能耗,其运用Hybrid-CS来收集前k个时刻的信号,以用作ARNS稀疏观测矩阵和稀疏基设计,并通过自适应调整稀疏观测矩阵内容来控制数据重构的精度。仿真结果表明,整个ARNS-DG过程既保证了数据重构的精度,又减少了网络能耗和数据量。 [1]徐平平,刘昊,褚宏云,等. 无线传感器网络[M]. 北京:电子工业出版社,2013:15-28. [2]Luo C,Wu F,Sun J,et al. Compressive Data Gathering for Large-Scale Wireless Sensor Networks[C]//The 15th Annual International Conference on Mobile Computing and Networking. New York:ACM Press,2009:145-156. [3]牛玉刚,甘峰浩,胡源. 基于压缩感知的拥塞控制机制[J]. 控制与决策,2015,30(2):246-250. [4]Wu X G,Xiong Y,Huang W C,et al. An Efficient Compressive Data Gathering Routing Scheme for Large-Scale Wireless Sensor Networks[J]. Computers and Electrical Engineering,2013,39(6):1935-1946. [5]陈正宇,杨庚,陈蕾,等. 基于压缩感知的WSN长生命周期数据收集方法[J]. 电子与信息学报,2014,36(10):2343-2349. [6]Luo C,Wu F,Sun J,et al. Efficient Measurement Generation and Pervasive Sparsity for Compressive Data Gathering[J]. IEEE Trans Wireless Communications,2010,9(12):3728-3738. [7]Laska J N,Davenport M A,Baraniuk R G. Exact Signal Recovery from Sparsely Corrupted Measurements Through the Pursuit of Justice[C]//Conference of the Forty-Third Asilomar Conference on Signals,Systems and Computers. Pacific Grove:IEEE Press,2009:1556-1560. [8]张美燕,蔡文郁. 融合K均值分簇MST路由的无线传感网压缩采样技术[J]. 传感技术学报,2015,28(9):1402-1407. [9]焦李成,杨淑媛,刘芳,等. 压缩感知回顾与展望[J]. 电子学报,2011,39(7):1651-1662. [10]Quer G,Masiero R,PillonettoG. Sensing,Compression,and Recovery for WSN:Sparse Signal Modeling and Monitoring Framework[J]. IEEE Trans Wireless Communications,2012,11(10):3447-3461. [11]Wu X G,Xiong Y,Yang P L,et al. Sparsest Random Scheduling for Compressive Data Gathering in Wireless Sensor Networks[J]. IEEE Trans Wireless Communications,2014,13(10):5867-5877. [12]Ranieri J,Chebira A,Vetterli M. Near-Optimal Sensor Placement for Linear Inverse Problems[J]. IEEE Trans Signal Processing,2014,62(5):1135-1146. [13]周锋,曾雪迎,杨力华. 一种基于正则化的稀疏表示方法[J]. 数学学报,2015,58(4):649-660. [14]Xie R T,Jia X H.Transmission-Efficient Clustering Method for Wireless Sensor Networks Using Compressive Sensing[J]. IEEE Trans Parallel and Distributed Systems,2014,25(3):806-815. [15]杜海韬,李强,丁广太,等. WSN中基于链路质量和节点能量的AODV路由算法研究[J]. 传感技术学报,2016,29(7):1042-1048. [16]Liu X,Luo J,Rosenberg C. Compressed Data Aggregation:Energy-Efficient and High-Fidelity Data Collection[J]. IEEE Trans Networking,2012,21(6):1722-1735. [17]Bodik P,Hong W,Guestrin C,et al. Intel Lab Data[DB/OL]. http://db.csail.mit.edu/labdata/labdata.html,2004. A Data Gathering Algorithm on WSN Based on AdaptiveRepresentative Nodes Selection* XIEChengyang1,NIUYugang1*,CHENGBei2 (1.Key Lab of Advanced Control and Optimization for Chemical Process,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China;2.Central Academe,Shanghai Electric Group Co.,Ltd.,Shanghai 200070,China) A shortcoming for the conventional compressive sensing(CS)method in wireless sensor network(WSN)is to require all nodes participating in data gathering process such that the waste of energy inevitably happen. In this paper,a data gathering method based on adaptive representative nodes selection is proposed,which not only ensures the accuracy of data reconstruction,but also reduces the number of nodes involved in data gathering. Firstly,a sparse basic is designed by combining principal component analysis(PCA)and CS;Secondly,according to the frame potential(FP)of sparse basic,a sparse measurement matrix is designed to choose representative nodes for reducing the number of nodes involved in data gathering. Thus,the data reconstruction accuracy in Sink node is guaranteed by adaptive controlling the sparse measurement matrix. Finally,it is shown via simulation results that the proposed method can reduce energy consumption and transmission of network,and ensure the accuracy of data reconstruction. WSN;representative nodes selection;compressive sensing;PCA;frame potential 谢成阳(1989-),男,湖北鄂州人,硕士研究生,研究领域为无线传感网络数据融合与拥塞控制,578245288@qq.com;牛玉刚(1964-),男,辽宁营口人,博士生导师,研究领域为随机系统,无线传感网络,微电网,acniuyg@ecust.edu.cn; 陈 蓓(1985-),女,浙江上虞人,博士生,研究领域为滑模控制,工业自动化,储能技术。 项目来源:国家自然科学基金项目(61673174) 2016-12-20 修改日期:2017-03-19 TP393 A 1004-1699(2017)08-1232-08 C:6150P 10.3969/j.issn.1004-1699.2017.08.018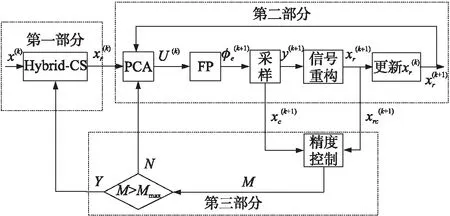
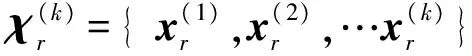
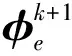
2 仿真实验

3 结束语


