基于AIC准则和时窗能量比的电缆局部放电在线检测与定位*

孙 抗,郭景蝶,杨延举,马星河

(1.河南理工大学电气工程与自动化学院,河南 焦作 454000;2.平顶山供电公司,河南 平顶山 467001)

基于AIC准则和时窗能量比的电缆局部放电在线检测与定位*

孙 抗1*,郭景蝶1,杨延举2,马星河1

(1.河南理工大学电气工程与自动化学院,河南 焦作 454000;2.平顶山供电公司,河南 平顶山 467001)

在利用多高频电流传感器进行电缆局部放电在线检测与定位时,针对局放信号初至时刻拾取精度不高影响定位精度的问题,提出一种基于AIC(Akaike’s Information Criterion)准则和时窗能量比的局放故障在线检测与精确定位方法。首先利用时窗能量比检测出局部放电发生的时窗,然后求取确定时窗的局部AIC特征曲线,并基于AIC准则精确拾取局放信号初至时刻。最后,运用到达时间法对局放源进行定位。仿真结果表明,该方法定位精度高,抗噪声干扰能力强,在-2 dB的噪声环境下可实现99.85%的定位准确率,具备工程实用价值。

局放放电;定位;时窗能量比;AIC准则;到达时间法

电缆局部放电(以下简称局放)信号的在线检测与定位对于电缆绝缘状况的诊断具有十分重要的意义[1-2]。高频电流法通过高频电流传感器(HFCT)耦合局放电流产生的电磁信号来检测局放信号,是目前运用最普遍的局放检测方法[3]。行波反射法(TDR)和到达时间法(ATA)是基于高频电流的常用局放定位方法。覃剑等分别运用上述方法对电缆局放源进行定位,但其定位的精度高度依赖于局放信号初至时刻的拾取精度[4]。郑文栋等采用AIC准则并联合多种传感器对局放源进行定位,但AIC方法只能用于局放信号初至时刻的拾取,并不能进行局放事件的识别,难以在线实现故障精确定位[5]。孟光韦等提出了基于时域反射原理的阈值法、峰值法对电缆局放源进行定位。但其定位精度受噪声和波形畸变影响较大,在实际应用中难以保证[6]。高树国等采用小波模极大值法进行局放定位,但该方法易受噪声影响产生多个伪极值点[7]。

时窗能量比在检测局放事件时简捷、高效,但拾取信号初至时刻的精度不高。AIC准则对波至时间的拾取精度远高于时窗能量比,但其仅适用于确定的局放事件时窗内,对于在线监测的时间序列,AIC准则难以有效检测局放事件。结合上述两种方法的优点,提出基于时窗能量比和AIC准则两步法的局放在线检测与定位方法。仿真结果表明,该方法能够有效克服现有方法局放初至时刻拾取精度不高的缺陷,且对噪声具有很强的适应能力,能够有效实现电缆局放故障的在线检测与精确定位。

1 基于AIC准则的局放初至时刻拾取

1.1 问题描述

在电缆局放在线定位应用中,由于噪声干扰、高频信号衰减、频散和反射等原因,TDR方法通常只适用于短距离局放定位。对于较长距离的电缆,可利用多传感器ATA法,通过比较局放信号到达各传感器的时间差实现局放源定位[8]。如图1所示,在电缆本体上安装3个传感器,首尾两端A、B间距离为L,传感器C位于AB中点。若同一局放信号到达两端传感器的时刻分别为t1、t2,则局放源与A端的距离为:

X=0.5[(t1-t2)v+L]

(1)

式中:v为局放信号在电缆中的传播速度。

由式(1)可知,ATA法的定位精度高度依赖于局放信号初至时刻的拾取精度。人工拾取精度虽高,但并不适用于在线定位。而现有的自动拾取方法拾取精度受噪声的影响较大。因此,能否在线高精度拾取局放初至时刻是电缆局放在线检测与定位的关键。

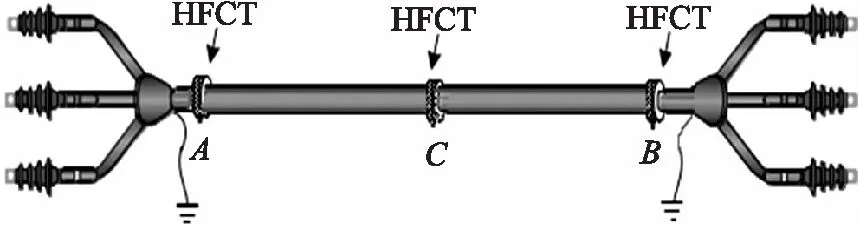
图1 多传感器安装示意图

1.2 AIC(Akaike)信息准则

AIC准则是一种衡量统计模型拟合优良性能的标准,可以权衡所估计模型的复杂度和模型拟合数据的优良性[9]。该准则采用AIC特征值衡量两个模型间的相对信息距离。信息距离越大,其拟合性越差,AIC特征值越小,因此,可利用AIC特征值来表示两个模型拟合度。AIC准则因其优良的性能和较高的精度被广泛应用地震预报、车辆设计、电源建模等领域[10-11]。

将AIC准则应用于电缆局放信号初至时刻的自动拾取。在信号检测时,若信号只含噪声分量,分量间统计特性相近,其拟合度较高,AIC特征值也较大。若信号中含有局放脉冲信号,由于噪声分量和局放分量具有不同的统计性质,在最小平方意义下两类信号间的拟合度最低,其AIC特征值最小。基于以上分析,AIC最小特征值对应的时刻即为局放信号初至时刻。

在信息论中,常用信息距离衡量信号间的拟合度。假设f为信号理想模型,g为其估计模型。用模型g近似f所带来的信息损失称之为两个模型间的Kullback-Leibler信息距离(K-L距离),其定义如式(2)所示。

(2)

通过比较两个模型的K-L距离大小,可以判断出两个模型的拟合程度。由于

E[lgg(X|θ)]=∫f(x)lgg(x|θ)dx

(3)

E表示f分布的数学期望,E[lgf(x)]为仅与f相关的定值。整理式(2)得:

I(f,g)=E[lgf(x)]-E[lgg(x|θ)]

=C-E[lgg(x|θ)]

(4)

定义I(f,g)-C为相对K-L距离,则:

I(f,g)-C=-E[lgg(x|θ)]

(5)

(6)

对于式(6)的比较存在过估计,过估计的量近似等于需要估计模型的参数个数K+1,即

(7)

因此,Akaike定义了期望K-L距离估计为模型的挑选准则,称为AIC准则。AIC特征值为:

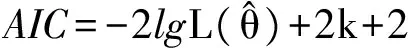
(8)

由上述推导可知,AIC特征值可有效衡量信号分量之间的拟合度,为局放信号初至时刻拾取提供计算依据。

1.3 基于AIC准则的波至时刻拾取

Akaike首先提出AIC准则,并将其应用于自回归(AR)模型中。该理论指出,一个时间序列可以分为几个局部稳定的时段,每一个时段都可以用AR模型来拟合[12-13]。由于噪声信号与局放信号性质不同,其AR模型也存在差异。在电缆局放在线定位时,将HFCT传感器测得的时间序列分为两个局部稳定的时段,每一段用AR模型来模拟。寻找将时间序列分为两个局部稳定时段的最佳分割点,该点处的AIC特征值最低,即局放初至时刻。如图2(a)所示,某时刻向采样信号注入一局放脉冲,其对应的AIC特征曲线如图2(b)所示。可以看出,AIC特征最小值点与脉冲注入时刻保持一致,可用于局放初至时刻的拾取。

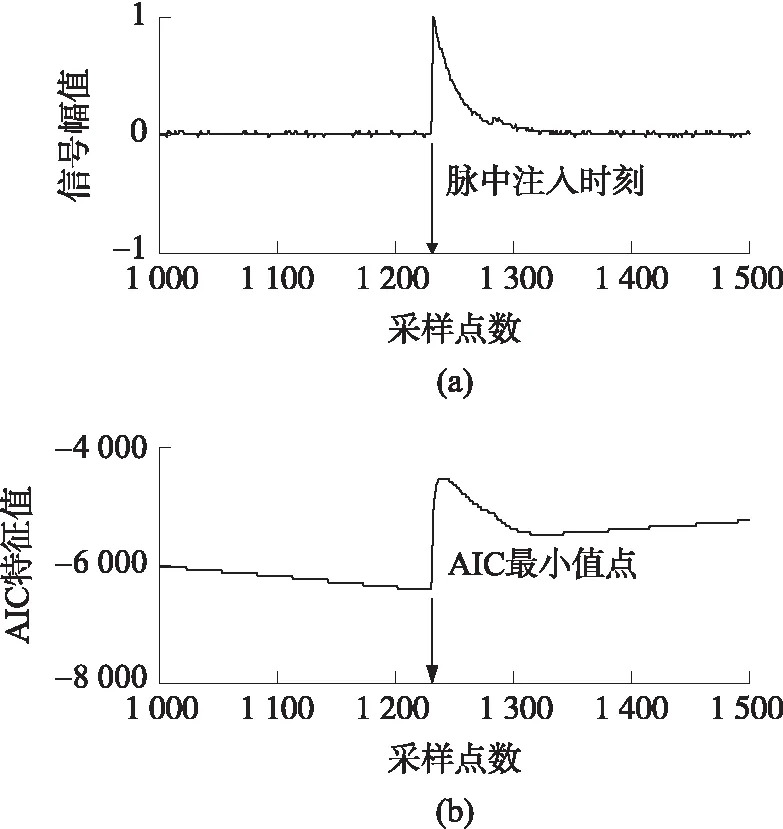
图2 局放初至时刻与AIC特征最小值对应关系

对于包含局放事件的时间序列[xn],局放初至时刻将该序列分为两个局部稳定的时段:局放到达前时段和到达后时段。每一个时段均能用AR模型来拟合:

(9)

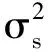
假设第k点是两个局部稳定时段的最佳分界处,用AR模型系数来求取两个时段的误差,并求取其最大对数似然函数得:

(10)

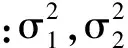
(11)

由于局放信号AR模型的阶数远小于采样点数,则式(11)可以简化为:

AIC(k)=klg[var(x[1,k])]+

(N-k-1)lg[var(x[k+1,N])]+C

(12)

式中:var表示数据序列的方差。

利用式(12)可直接得到时间序列[xn]的AIC特征曲线,其最小值点即对应局放信号的初至时刻。

2 基于时窗能量比的局放事件检测

在包含局放事件的时间序列中,AIC准则能够实现局放初至时刻的高精度拾取,但其自身却不能实现局放事件的自动检测。即使在不含局放事件的纯噪声记录中也总会出现一个AIC最小值点(1 424),但此点却没有任何意义,如图3所示。因此,局放源在线定位首先要识别局放信号,并确定出局放发生的时窗。

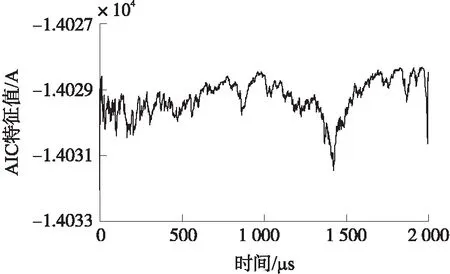
图3 纯噪声信号的AIC特征曲线

时窗能量比经常应用于地震信号检测,本文将其引入,用于确定局放发生的时窗。对于监测到的时间序列[xn],对时间轴上第i个采样点邻域附近取一时窗,时窗样点长度为2 m,该采样点i即为时窗中心,则后时窗与前时窗之间的能量比值可表述如下:

(13)

考虑到式(13)稳定性,可以增加一个稳定性因子,则能量比可定义为:

(14)

式(14)的意义在于,当初至信号到达后,通过检测时窗能量比R是否大于给定的阈值,判断是否有局放事件发生。若未检测到符合条件的能量比值则循环至下一时刻,若检测出局放事件,则可确定出以局放事件点为中心,大小为2m的时窗[xn],对[xn]运用AIC准则即可得到局放信号初至时刻。

3 基于两步法的电缆局放源定位

时窗能量比法能通过比值R的最大值点确定局放的初至时刻,但精度不高。AIC准则可实现初至时刻的高精度拾取,且其精度高于时窗能量比法,但不能识别局放事件,无法进行在线检测与定位。基于此,提出一种联合时窗能量比和AIC准则的两步法实现局放信号初至时刻的高精度自动拾取。首先利用时窗能量比检测局部放电事件发生的时窗,然后对确定的时窗采用局部AIC准则实现局放信号初至时刻的拾取。图4为时窗能量比与两步法对比试验结果。对于含局放事件的信号波形,人工拾取的波至时间点为1 231(图4a);取时窗宽度为200,时窗能量比拾取初至时刻为1 179(图4(b));两步法拾取初至时刻为1 230(图4(c))。经上述对比分析可知,仅采用时窗能量比得到的初至时刻误差较大,而两步法得到的初至时刻更接近真实值。

图4 局放事件的检测结果对比

如上所述,两步法可得到传感器A、B、C处的波至时刻,分别记为tA(aic)、tB(aic)、tC(aic)。接下来,可通过这三个时刻值确定局放源范围,并进一步通过多传感器ATA法计算出局放信号在电缆中的传播速度。解决了因电缆型号、状态以及信号频率等多种因素导致传播速度与经验固定速度存在差异的波速不定性问题。

若|tA(aic)-tC(aic)|<|tB(aic)-tC(aic)|,则局放源位于AC段,局放信号的传播速度为:

(15)

若|tA(aic)-tC(aic)|>|tB(aic)-tC(aic)|,则局放源位于BC段,局放信号的传播速度为:

(16)

若|tA(aic)-tC(aic)|=|tB(aic)-tC(aic)|,则局放源位于AB外的电缆两端,局放信号的传播速度为:

(17)

将算得的波速代入式(1)中,则局放源位于AC段时,距离A端的距离为:

(18)

局放源位于BC段时,距离B端的距离为:

(19)

4 仿真实验与结果分析

4.1 仿真实验模型与方法

利用PSCAD/EMTDC中的BergeronModel电缆模型对电缆局放系统进行仿真,验证时窗能量比和AIC两步法在电缆局放定位中的可行性。配置一根长1km的10kV电缆,将该电缆模型简化为3部分:导体层、屏蔽层和外皮,如图5所示。

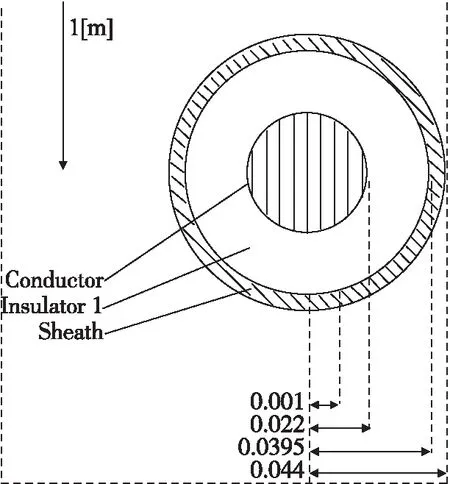
图5 电缆仿真模型

电缆参数如表1所示。

表1 10 kV电缆模型参数

局放波形上升沿陡峭并且持续时间短,在数学模型上可以用指数函数模型来等效:

f(t)=Ae-(t-t0)/τ

(20)

式中:A是信号的幅值,t0是信号发生时间,τ是衰减系数。当取A=2mV,τ=1μs时,放电模型如图6所示。

在距离A端100m处注入模拟脉冲,pscad仿真模型图如图7所示。

图6 指数函数放电曲线

利用传感器Ea1、Ea2、Ea3采集局放信号,如图8所示。可以看出局放信号通过不同长度电缆传输到达传感器的时间不同。

4.2 时窗长度对波至时刻拾取精度的影响

时窗能量比的拾取精度与所选时窗的长度相关,为探讨两步法拾取精度与时窗长度的关系,采用不同大小的时窗对同一时间序列进行局放初至时刻拾取,结果如表2所示。

图7 局部放电Pscad仿真模型

图8 传感器测得的局放信号

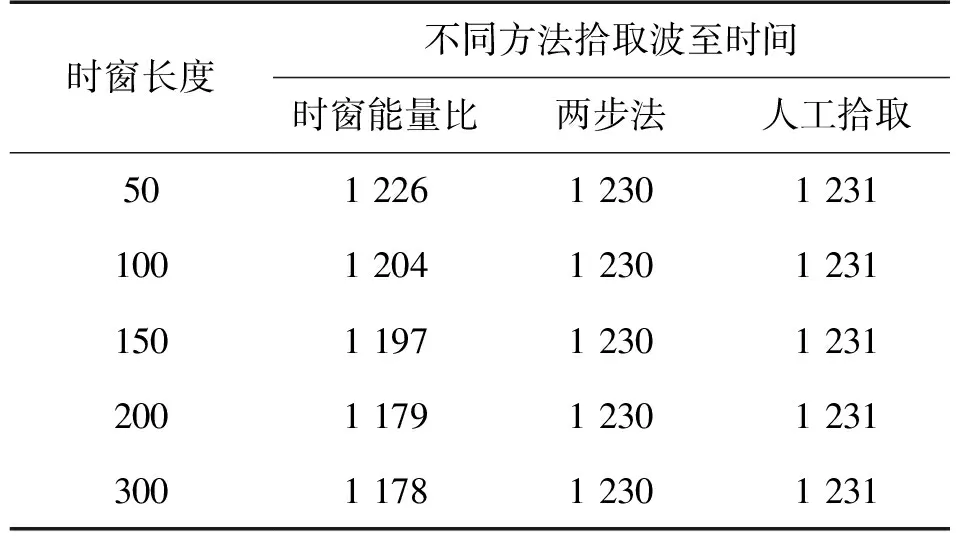
时窗长度不同方法拾取波至时间时窗能量比两步法人工拾取50122612301231100120412301231150119712301231200117912301231300117812301231

由表2可以看出,随着时窗长度的变大,时窗能量比拾取波至时刻的精度变低,而本文采用的两步法

并不受时窗长度影响,拾取的波至时刻与人工拾取的时刻几乎一致,拾取精度较高。

4.3 实验结果及分析

在现场使用环境下,测量噪声难以避免。为验证算法的实用性,对局放脉冲分别加入信噪比约为20 dB、4 dB、-2 dB的高斯白噪声。应用本文提出的两步定位算法,得到的AIC特征曲线如图9所示,其中图9(a)、图9(c)、图9(e)为不同噪声情况下的放电波形,图9(b)、图9(d)、图9(f)为其对应的AIC特征曲线。

表3为在不同信噪比情况下运用峰值法和两步法所得到的信号初至时刻以及运用ATA对长为1 km,局放源距离100 m的电缆进行在线局放故障检测与定位的结果。

由表3可知,峰值法和本文所提两步法的定位精度均受信噪比影响,但在同等噪声环境下,两步法的定位误差小于峰值法。在-2 dB的噪声环境下,基于两步法的定位方法可实现99.85%的定位准确率,具有更高的实用价值。

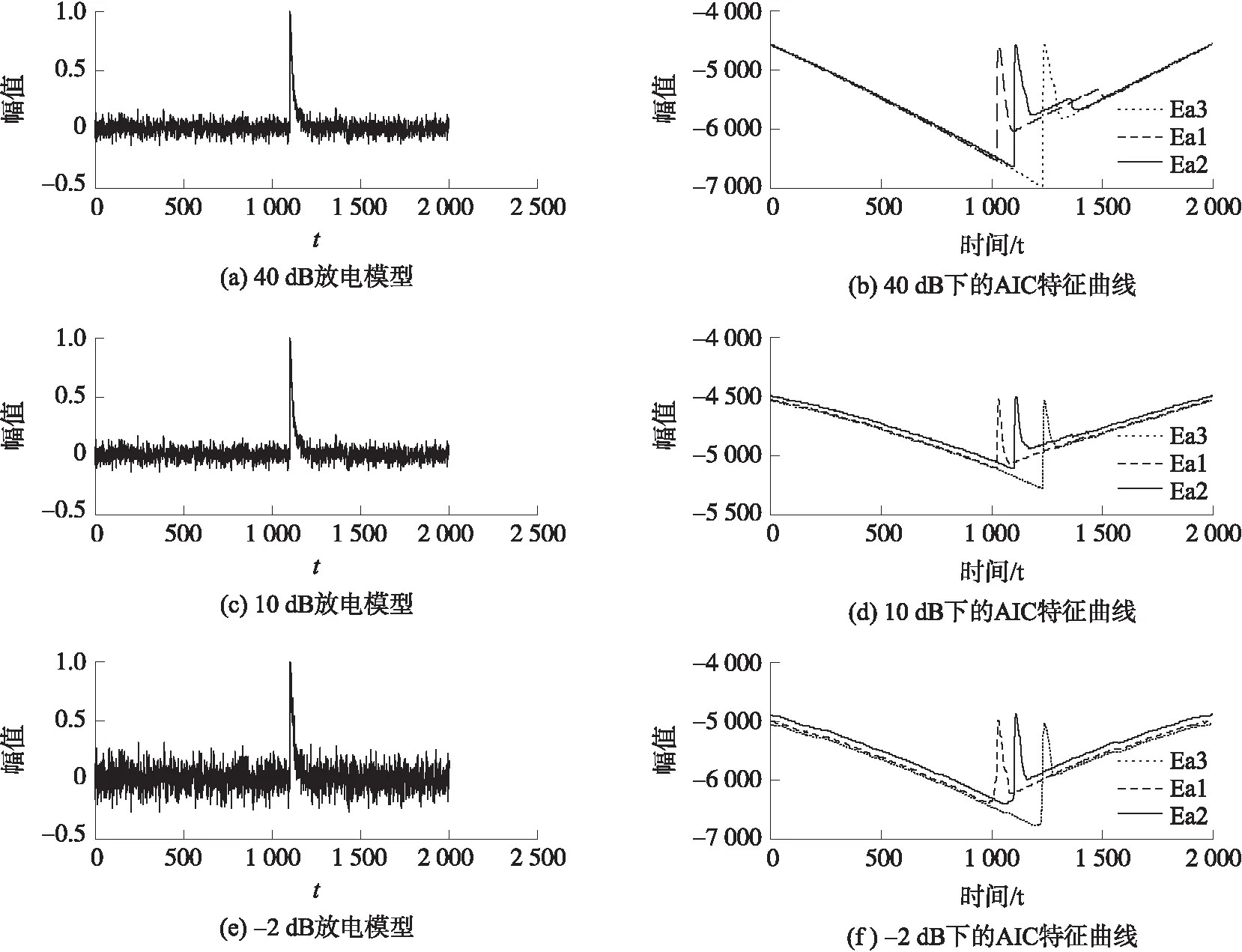
图9 不同噪声与对应特征曲线图

信噪比/dB两步法Ea1Ea2Ea3定位值/m误差/m峰值法Ea1Ea2Ea3定位值/m误差/m2010251102123099．60．4102711041233100．80．84102511021231100．80．8102811041233102．72．7-298710661199101．51．5102811041234103．83．8

5 结论

①本文提出的基于时窗能量比与AIC准则的两步法有效综合了两种方法的优点,可在线识别局放事件,并实现局放信号初至时刻的高精度拾取,从而有效提高了局放源在线定位精度。

②基于多传感器的ATA方法不仅实现了长电缆局部放电的在线检测,且解决了波速不定性问题,提高了在线定位的精度。

③相比于传统的阈值法、峰值法和小波模极值法,本文所提出的两步法对噪声具有更强的适应能力,具有重要的理论意义和工程应用价值。

[1]郭灿新,张丽,钱勇,等. XLPE电力电缆中局部放电检测及定位技术的研究现状[J]. 高压电器,2009,45(3):56-60.

[2]江秀臣,蔡军,董小兵,等. 110 kV及以上电压等级交联电缆在线监测技术[J]. 科学之友,2013,25(10):13-17.

[3]韦斌,王伟,李成榕,等. VHF钳型传感器在线检测110 kV XLPE电缆局放[J]. 高电压技术,2004,30(7):37-39.

[4]覃剑,葛维春,邱金辉,等. 输电线路单端行波测距法和双端行波测距法的对比[J]. 电力系统自动化,2006,30(6):92-95.

[5]郑文栋,杨宁,钱勇,等. 多传感器联合检测技术在XLPE电缆附件局部放电定位中的试验研究[J]. 电力系统保护与控制,2011,39(20):84-88.

[6]孟光韦,黄培光,王萌,等. 基于TDR技术的弹上电缆网无损在线检测技术研究[J]. 电子测试,2016(14):55-56.

[7]高树国,刘贺晨,范辉,等. 考虑波速特性的小波变换模极大值法的电力电缆局部放电定位研究[J]. 电网技术,2016,40(7):2244-2250.

[8]范新桥,朱永利. 基于双端行波原理的多端输电线路故障定位新方法[J]. 电网技术,2013,37(1):261-269.

[9]俞倩雯,李克强. 基于AIC信息量准则的车辆油耗建模与评估[J]. 汽车工程学报,2014,4(3):165-171.

[10]贾瑞生,谭云亮,孙红梅,等. 低信噪比微震P波震相初至自动拾取方法[J]. 煤炭学报,2015,40(8):1845-1852.

[11]商云龙,张奇,崔纳新,等. 基于AIC准则的锂离子电池变阶RC等效电路模型研究[J]. 电工技术学报,2015,30(17):55-62.

[12]王晓伟,刘占生,窦唯. 基于AR模型的声发射信号到达时间自动识别[J]. 振动与冲击,2009,28(11):79-83.

[13]张朋,范福玲,杨益,等. 基于时间序列模型的超声信号滤波算法研究[J]. 传感技术学报,2015(3):396-400.

孙 抗(1982-),男,2004年于哈尔滨工业大学获得学士学位,2011年于北京理工大学获得博士学位,现为河南理工大学副教授,主要研究方向为设备在线监测、智能电器等。

On Line Partial Discharge Detection and Localization Based onAIC Criterion and Time-Window Energy Ratio*

SUNKang1*,GUOJingdie1,YANGYanju2,MAXinghe1

(1.School of electrical engineering and automation,Henan Polytechnic University,Jiaozuo He’nan 454000,China;2.Pingdingshan Power Supply Company,Pingdingshan He’nan 467001,China)

Based on AIC(Akaike’s Information Criterion)criterion and time window energy ratio,the method of PD on-line detection and fault location was proposed to solve the problem that the positioning accuracy was affected by the low picking accuracy of PD signal arrival time,when using the multi high frequency current sensor to realize the online detection and location of partial discharge on cable. Firstly,the time window energy ratio was used to the time window,and the AIC characteristic curve of the certain window was obtained,then the AIC criterion was used to accurately pick up the initial arriving moment of signal. Finally,the PD source was located by the method of arrival time. The simulation results show that this method,which has high engineering practical value,not only has high precision and strong anti-interference ability,but also can achieve 99.85% localization accuracy in -2 dB noise environment.

partial discharge;location;time window energy ratio;AIC criterion;arrival time

项目来源:国家自然科学基金河南省联合基金项目(U1404522);河南省产学研合作项目(132107000027)

2016-11-26 修改日期:2017-03-28

TM726.4

A

1004-1699(2017)08-1209-06

C:7230

10.3969/j.issn.1004-1699.2017.08.014