基于重力四元数的陀螺漂移估计与补偿*
杨金显,杨 闯
(河南理工大学电气工程与自动化学院导航制导实验室,河南 焦作 454003)
基于重力四元数的陀螺漂移估计与补偿*
杨金显*,杨 闯
(河南理工大学电气工程与自动化学院导航制导实验室,河南 焦作 454003)
为提高钻探中的钻具姿态测量精度,提出一种基于重力四元数的MEMS惯性随钻姿态测量方法。采用MEMS惯性器件构建钻具姿态测量系统,把加速度计数据解算的姿态四元数作为观测四元数,陀螺仪数据解算的姿态四元数作为误差四元数;然后将陀螺仪漂移融入误差四元数,建立重力四元数估计陀螺仪误差四元数的模型,采用最小二乘法估计陀螺仪三轴漂移,进而补偿陀螺仪姿态四元数;通过补偿后的姿态四元数解算出钻具姿态。最后设计了转台、振动台实验和钻进模拟实验,实验结果表明,姿态四元数补偿后的井斜角和工具面角漂移由平均10 °/h减小到约0.2 °/h,方位角误差由平均12 °/h减小到约0.46 °/h,实现了加速度计补偿陀螺的三轴漂移,表明该方法能够有效提高钻具的姿态测量精度。
惯性随钻测量;陀螺漂移估计;重力四元数;姿态解算
近年来,基于MEMS加速度计/陀螺仪的微惯性姿态测量单元(MIMU)以其成本低、体积小、寿命长、集成化、抗冲击能力强和可靠性高等优势,不但在石油钻井、地质勘探和非开挖领域得到广泛应用,近几年也逐步推广到煤矿领域,如煤层气(瓦斯)抽采、底板加固、注浆堵水的钻孔等,这就要求实时对钻具的姿态进行测量和监测,以保障钻具的正常运行。采用MEMS惯性器件构造的惯性随钻测量单元MIMU,通过敏感的钻具三轴加速度和角速度经过解算可得钻具井斜角θ、工具面角φ、方位角ψ,陀螺仪作为MIMU的主要测量元件,但由于陀螺仪存在漂移,长时间累积计算会产生较大误差,需要利用辅助传感器对陀螺漂移进行估计和误差补偿。尽管国外的惯性随钻测量技术已趋于成熟,但严格的技术封锁,因此进行相关研究具有重要意义。
陀螺仪倾角信息补偿一般不是问题,可以靠MIMU中加速度计来完成,由于加速度计精度要高于陀螺仪,且无累计误差,结合陀螺仪和加速度计解算的结果可以获得较高精度倾角信息,这也是国内外加速度计在随钻测量中大量使用的原因[1-4]。但加速度计不能很好的获得方位角信息,难以对陀螺进行方位角修正,而用磁强计辅助的方式进行方位修正,需建立精确地磁场模型和屏蔽钻具本身的磁干扰以及外界磁干扰[2,4-7],考虑到随钻测量复杂的磁场环境磁强计辅助方式很难实施,因此补偿陀螺方位漂移这个重担还得落到加速度计身上。
由上面分析,若简单通过加速度计解算钻具角度补偿陀螺漂移,仅能补偿陀螺倾角信息而钻具方位角补偿却无能为力。为实现加速度计对陀螺仪三轴漂移的补偿,李启光等对6只加速度计按回转轴对称布局建立加速度与角速度数学模型,并利用Kalman滤波对该解算角速度与陀螺仪的输出进行融合补偿陀螺仪漂移[8],虽实现对陀螺漂移全补偿,但需要对加速度计严格对称安装,较难应用到随钻测量。Churchill提出了利用加速度计估计陀螺处于铅垂方向时的漂移以修正航向角的方法[9],该方法需要确保旋转是绕水平方向以保证修正精度,不适用于MIMU姿态角处于任意值的情形。颜翚等建立了陀螺漂移随机游走模型,并用加速度计陀螺仪的低频值作为观测量,通过扩展卡尔曼滤波算法进行钻具姿态的导航推算[10],在静态下虽有一定效果,但强振动强冲击条件下陀螺漂移模型不一定适用。吴哲明提出一种通过IMU旋转实现加速度计估计陀螺漂移方法,建立了倾角误差和陀螺漂移之间的数学模型[11],需要稳定旋转机构驱动,在随钻测量强振动强冲击环境很难实现。
由于加速度计精度要高于陀螺仪,且无累计误差,鉴于此,为进一步解决加速度计难以估计陀螺仪三轴漂移,不通过加速度计求角度补偿陀螺仪积分角度误差,在不增加额外辅助部件情况下,根据四元数旋转理论,建立重力四元数估计陀螺仪误差四元数模型,采用最小二乘法估计陀螺仪三轴漂移,进而补偿陀螺仪姿态四元数,通过补偿后的姿态四元数解算出钻具姿态。最后设计了转台实验、振动实验和钻进模拟实验,实验结果表明,该方法能够有效提高钻具的姿态测量精度。
1 钻具姿态四元数描述
假定地理坐标系作为参考坐标系,有n系oxnynzn(正向分别为东、北、天),钻具坐标系b系oxbybzb。参考坐标系到钻具坐标系的单位旋转四元数记为q=[q1,q2,q3,q4]T,有如下关系;
(1)
通过四元数有关旋转理论可将n系向b系的坐标旋转变换过程用坐标变换矩阵表示为:
(2)
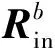
(3)
由式(3)求取当前钻具姿态角,需要先获取钻具当前姿态四元数,钻具姿态四元数可分别由加速度计、陀螺仪数据解算获得,理想情况下钻具姿态四元数=重力四元数=陀螺仪姿态四元数,陀螺仪四元数通过陀螺仪敏感钻具三轴角速度来完成。由于陀螺仪漂移导致陀螺仪四元数存在累积误差,加速度计精度要高于陀螺仪,且无累计误差,但易受钻具振动影响[13-14],因此为获取较高精度钻具姿态四元数,进而提取较高精度姿态角,需要融合重力四元数和陀螺仪四元数,钻具姿态解算过程如图1所示。
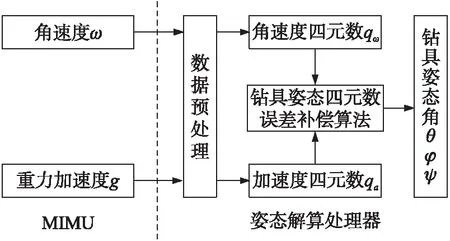
图1 钻具姿态角四元数解算过程
2 姿态四元数误差补偿算法
2.1 重力四元数
钻具停止钻进时加速度计测量的钻具主要为重力加速度及测量噪声。加速度计测量的钻具重力向量记为a=[ax,ay,az]T;在参考系(地理系)中,归一化的重力向量记为gn=[0,0,1]T,经式(2)坐标变换得钻具坐标系下的重力向量gb为:
(4)
联立式(1)、式(4),求取当前加速度姿态四元数qa(k+1),有[15]:
qa(k+1)=q(k+1)+qa0(k+1)
(5)
式中:qa0(k+1)为加速度计提取重力加速度过程中噪声四元数,作为白噪声四元数处理。q(k+1)为钻具真实姿态四元数(k+1表示当前时刻,k表示上一时刻,k=0,1,2,…,下同)。
2.2 陀螺仪误差四元数传递模型
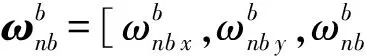
(6)
式中:q表示当前钻具真实姿态四元数,其一阶龙格—库塔计算式为:
(7)
T为角速度采样周期。式(6)、式(7)为理想角速度分量下姿态四元数表示,实际角速度由与钻具固连陀螺仪所测,陀螺仪存在漂移,其漂移模型简记为[11]:
(8)
式中:ω为陀螺仪所测三轴角速度向量,ω0=[ω0x,ω0y,ω0z]T为陀螺漂移误差向量。陀螺漂移是一个随机渐变过程,在相邻采样间隔认为其不变[16]。式(7)基于陀螺所测角速度通过迭代加求取当前时刻钻具姿态四元数,因陀螺漂移会有累计误差,若不加以补偿,短时内就会积累很大姿态四元数误差,因此需对陀螺漂移估计并补偿修正实时姿态四元数。
考虑式(8)陀螺仪角速度误差模型,联立式(6)、式(7)得当前时刻陀螺仪钻具姿态四元数:
(9)

2.3 重力四元数估计陀螺漂移算法
当前时刻钻具真实姿态四元数无法精确获得,鉴于加速度计精度高于陀螺仪,以当前加速度姿态四元数观测陀螺仪姿态四元数,由式(5)、式(9)可得重力四元数观测陀螺仪四元数误差最小二乘估计模型:
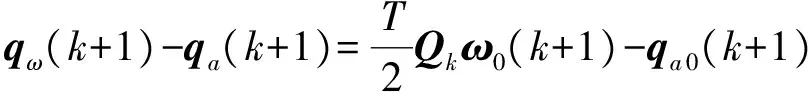
(10)

(11)
将式(11)陀螺漂移估计值代入式(9)结合当前陀螺仪姿态四元数,可得当前钻具姿态四元数最佳估计值:
(12)
将代入(12)代入式(3)四元数计算钻具姿态即得当前时刻钻具最佳姿态估计。
基于上述原理,重力四元数估计陀螺漂算法流程如图2所示。
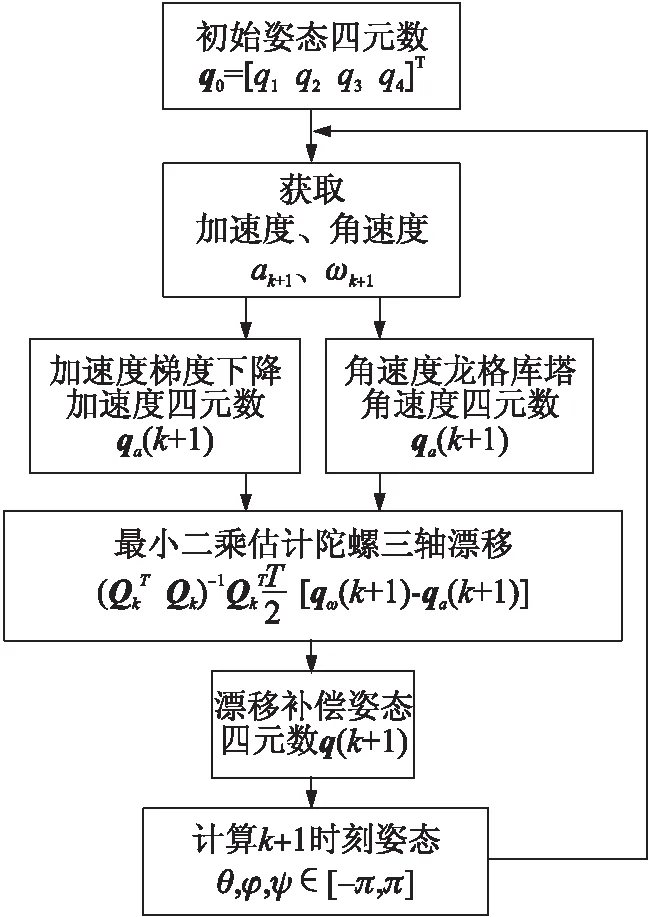
图2 重力四元数估计陀螺漂移流程图
3 实验设计及结果分析
3.1 转台实验


图3 MIMU转台实验

图4 转台实验陀螺仪漂移补偿前后姿态角误差
观察图4可知,陀螺仪在较短时间内漂移累积误差较小,长时间工作累计误差较大,且工作时间越长,累计误差越大,因此需要对陀螺漂移进行估计与补偿。经过1h的姿态解算,加速度计连续补偿陀螺漂移,井斜角误差由9.35 °/h减小到0.17 °/h;工具面角误差由9.35 °/h减小到0.19 °/h;方位角误差由9.96 °/h减小到0.28 °/h,显著减小了因陀螺漂移造成的姿态解算误差,可见算法实现了加速度计对陀螺仪的三轴漂移估计与补偿。同时,实验发现当倾斜角小于3°或接近90°时,方位角变化引起的重力四元数变化较小,导致重力四元数观测陀螺方位轴漂移能力降低,致使方位角误差补偿能力略有降低。
3.2 振动台实验
为验证算法在钻进振动情况下估计并补偿陀螺漂移性能,设计了振动台实验,将设计的蓝牙MIMU以倾斜角45°固定于振动台,如图5所示,采集3 600sMIMU信号,用本文方法实时估计并补偿陀螺漂移,陀螺漂移补偿前后姿态解算误差随时间变化情况如图6所示。

图5 MIMU振动台实验
观察图6发现,加速度计补偿陀螺漂移前后井斜角误差由11.14 °/h减小到0.24 °/h;工具面角误差由10.09 °/h减小到0.42 °/h;方位角误差由12.63 °/h减小到0.38 °/h,虽显著减小因陀螺漂移造成的姿态解算累积误差,但由于受振动影响,重力估计并补偿陀螺漂移误差会有所增大。
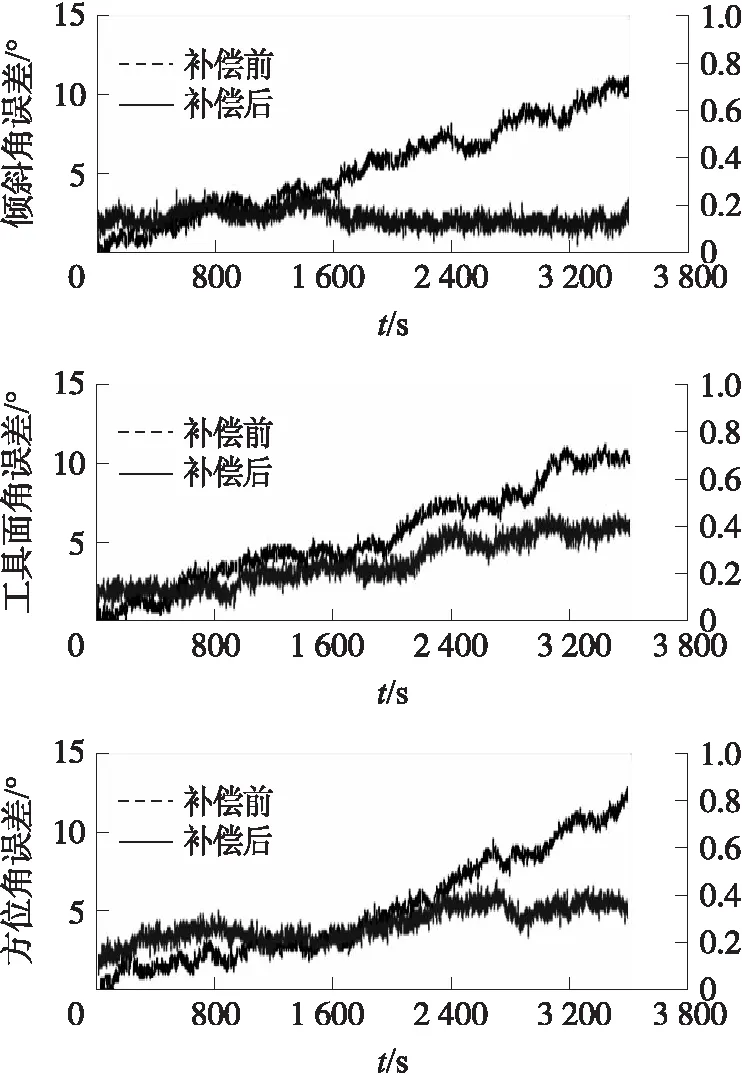
图6 振动台实验陀螺仪漂移补偿前后姿态角误差
3.3 钻进模拟实验
为进一步验证重力四元数估计陀螺漂移算法性能,设计了钻进模拟实验,将设计的蓝牙无线MIMU系统通过夹具固定于钻杆上部如图7所示,并通过转台对失准角进行标定。钻进过程存在振动冲击,为提高钻具姿态解算精度,硬件上采用高精度抗振MEMS加速度计和陀螺仪并做抗振处理(MIMU精度越高姿态结算精度也会越高);软件处理方法上由于陀螺仪抗振性能优于加速度计(可从加速度计和陀螺仪的工作原理上分析得知),在振动较大时用陀螺解算钻具姿态,振动较小时利用重力四元数估计并补偿陀螺漂移,可充分利用连接钻杆或人为控制停止钻进期间重力四元数估计并补偿陀螺漂移,进行重置姿态初始值。

图7 模拟钻进实验
实验开始前,先调整钻机倾斜角为45°并记录50s静止姿态数据;然后以初始倾斜角/方位角直行钻进,持续10 800s,每1 800s停止钻进模拟安装钻杆过程,通过蓝牙实时采集MIMU加速度、角速度及解算的姿态角数据,并在试验结束后对采集的角速度数据进行离线姿态角解算。为便于对比陀螺漂移补偿前后姿态角解算误差,本次实验仅对倾斜角和方位角解算误差进行测试,将实验开始前采集的多组倾斜角、方位角数据均值作为真值;将离线角速度解算的角度作为陀螺漂移补偿前角度数据,MIMU模块实时解算的角度为补偿后的角度。
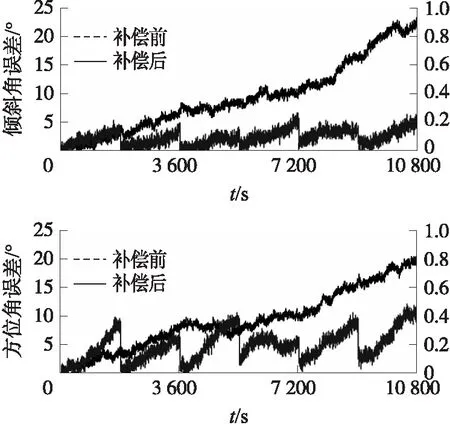
图8 钻进实验陀螺仪漂移补偿前后姿态角误差
图8为陀螺漂移补偿前后倾斜角/方位角解算误差对比结果,由图8可知,重力四元数间歇补偿陀螺漂移前后井斜角误差由11.15 °/h减小到0.22 °/h以内;方位角误差由10.18 °/h减小到0.46 °/h以内,显著减小因陀螺漂移造成的姿态解算累积误差。
4 结论
针对MIMU在惯性随钻测量中加速度计难以估计陀螺三轴漂移问题,本文通过四元数旋转理论,利用加速度姿态四元数与陀螺仪姿态四元数关系,建立重力四元数估计陀螺仪误差四元数模型,采用最小二乘法估计陀螺仪三轴漂移,进而补偿钻具姿态四元数,通过补偿后的姿态四元数解算出钻具姿态,利用连接钻杆或人为控制停止钻进期间进行重置姿态初始值。最后转台和振动台实验结果表明,陀螺漂移补偿修正后姿态估计精度有了明显提高,实现了加速度计估计陀螺仪三轴漂移,钻具倾角及方位角精度有了较大提高。钻进模拟实验,陀螺漂移补偿前后倾斜角误差由11.15 °/h减小到0.22 °/h以内;方位角误差由10.18 °/h减小到0.46 °/h以内,进一步说明了重力四元数间歇补偿陀螺漂移算法的有效性,计算量小,表明该方法有效能够提高钻具的姿态测量精度。
[1]Jurkov A S,Cloutier J,Pecht E,et al. Experimental Feasibility of the In-Drilling Alignment Method for Inertial Navigation in Measurement while Drilling[J]. IEEE Transactions on Instrumentation and Measurement,2011,60(3):1080-1090.
[2]Wang Z,Poscente M,Filip D,et al. Rotary In-Drilling Alignment Using an Autonomous MEMS-Based Inertial Measurement Unit for Measurement while Drilling Processes[J]. IEEE Instrumentation and Measurement Magazine,2013,16(6):26-34.
[3]杨全进,徐宝昌,左信,等. 旋转导向钻具姿态的无迹卡尔曼滤波方法[J]. 石油学报,2013,34(4):1168-1175.
[4]Xue Qilong,Leung H,Wang Ruihe,et al. Continuous Real-Time Measurement of Drilling Trajectory with New State Space Models of Kalman Filter[J]. IEEE Transactions on Instrumentation and Measurement,2016,65(1):144-154.
[5]徐涛,温东,孙晓磊. 基于加速度计和磁强计的方位测量与校正技术研究[J]. 仪器仪表学报,2009,30(10):2018-2022.
[6]Afzal M H,Renaudin V,Lachapelle G. Use of Earth’s Magnetic Field for Mitigating Gyroscope Errors Regardless of Magnetic Perturbation[J]. Sensors,2011,11(12):11390-414.
[7]高怡,汪跃龙,程为彬. 抗差自适应滤波的导向钻具动态姿态测量方法[J]. 中国惯性技术学报,2016,24(4):437-442.
[8]李启光,张海龙. 基于六加速度计的陀螺仪漂移补偿算法的研究[J]. 传感器与微系统,2009,28(12):42-44.
[9]Churchill D L. Inertial Measurement System with Self Corrertion[P]. No.8010308.USA,2011.
[10]颜翚,葛彤,杨柯,等. 水下攻泥器随钻姿态惯性测量方法[J]. 上海交通大学学报,2012,46(03):446-450,457.
[11]吴哲明,孙振国,张文增,等. 基于惯性测量单元旋转的陀螺漂移估计和补偿方法[J]. 清华大学学报(自然科学版),2014,54(9):1143-1147.
[12]吴涛,白茹,朱礼尧,等. 基于卡尔曼滤波的航姿参考系统设计[J]. 传感技术学报,2016,29(4):531-535.
[13]Rohac J,Reinstein M,Draxler K. Data Processing of Inertial Sensors in Strong-Vibration Environment[C]//Intelligent Data Acquisition and Advanced Computing Systems(IDAACS),2011 IEEE 6th International Conference.IEEE,2011,1:71-75.
[14]Alam M,Rohac J. Adaptive Data Filtering of Inertial Sensors with Variable Bandwidth[J]. Sensors,2015,15(2):3282-3298.
[15]Sebastian O H Madgwick,Andrew J L Harrison,Ravi Vaidyanathan. Estimation of IMU and MARG Orientation Using Agradient Descent Algorithm[C]//IEEE International Conference on Rehabilitation Robotics. USA,2011:332-338.
[16]Mahony R,Euston M,Kim J,et al. A Non-Linear Observer for Attitude Estimation of a Fixed-Wing Unmanned Aerial Vehicle without GPS Measurements[J]. Transactions of the Institute of Measurement and Control,2011,33(6):699-717.
Gyro Drift Estimation and Compensation Based on Gravity Quaternion*
YANGJinxian*,YANGChuang
(Navigation and Guidance Laboratory,School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo He’nan 454003,China)
In order to decrease the attitude measurement error while drilling,an gravity quaternion estimating triaxial gyro drift-based(AQEGD)attitude measurement algorithm is proposed using an inertial sensor composed of a triaxial accelerometer and a triaxial gyroscope. The gravity quaternion based on accelerometer data is regarded as an observation vector,the gyro quaternion based on gyro data as an error vector blended in triaxial gyro drift;The triaxial gyro drift errors are sensed by the gravity quaternion using the linear least square estimation algorithm,by which the gyro quaternion used to calculate drilling tools dynamic attitude orientation is compensated;At last turntable experiment,shaking-table experiment and drilling experiment are conducted to verify the performance of the proposed algorithm in various dynamic condition settings and to provide further insight into the variations in the estimation accuracy. Furthermore,the experiments indicate that the proposed AQEGD can lower the triaxial gyro drift,with corresponding orientation average errors of deviation angle and tool face angle from 10 °/h(before compensation)to 0.2 °/h(after compensation),azimuth from 12 °/h to 0.46 °/h.
inertial measurement while drilling;gyro drift estimation;gravity quaternion;attitude algorithm

杨金显(1980-),男,山东曹县人,博士,副教授,硕士生导师,1999~2008年于哈尔滨工程大学获得学士、硕士和博士学位,主要从事MEMS惯性测量及在随钻、电网运动和变形监测中的应用研究,yangjinxian@hpu.edu.cn;杨 闯(1992-),男,河南滑县人,现为河南理工大学电气工程与自动化学院硕士研究生,主要从事惯性测量研究,yang_ch126@126.com。
项目来源:国家自然科学基金项目(41672363,U1404510,61440007);河南省科技攻关项目(172102210289);河南省创新型科技人才队伍建设工程项目(CXTD2016054);河南省高校基本科研业务费专项资金项目(NSFRF1619);河南理工大学杰出青年基金项目(J2017-5)
2017-01-25 修改日期:2017-04-18
TH763
A
1004-1699(2017)08-1187-06
C:7210
10.3969/j.issn.1004-1699.2017.08.010

