目标火力分配的优化算法

文/陈龙马亚平

目标火力分配的优化算法

文/陈龙1马亚平2

火力分配问题是一个规划问题，火力分配优化问题是作战仿真中的一个重要内容，其算法的优劣决定了火力分配优化结果，该结果是影响战争胜败的关键因素。本文通过分析目标火力分配优化算法发展历程，将火力分配优化算法归纳总结为常规解析火力分配法、智能进化火力分配法、混合式火力分配法三种方法，并分析总结各自的特点，最后对MOEA/D优化算法进行了初步研究。

火力分配 优化算法 MOEA/D算法

集中优势兵力，以多击少，这是战争中一条基本作战原则。伟大的军事家毛泽东说过：“集中优势兵力，各个歼灭敌人。”克劳塞维茨也指出：“数量上的优势应该看作是基本原则，不论在什么地方都应该是首先和尽量争取的。”时至今日，如何精确用兵，做到战斗效能精确匹配、数量规模合理够用，量敌用兵，保存战力，以最小代价夺取最大作战效果是对这一基本原则的发展和延伸。随着信息化武器装备的不断更新换代，其相应的打击能力也不断提高，火力分配的优化直接影响着战争的进程和胜负。实际作战中，由于作战火力单元资源有限，难以做到对所有目标进行均匀打击和有效覆盖。因此需要在满足火力资源约束条件下，紧紧围绕作战使命，合理分配火力，以综合效能作用于敌要害和关节，争取以最小的代价最大限度地达成作战使命。火力分配问题实际上是一个多目标优化问题，国内外针对火力分配问题的研究非常广泛，而且根据不同的火力和目标提出相应的优化算法。很多算法已经被运用于火力分配优化中，大致可以分为常规解析火力分配法、智能进化火力分配法、混合式火力分配法三种方法。

1 常规解析火力分配法

常规解析火力分配法是将求解问题抽象化、形象化形成数学表达式，利用若干个数学表达式建立相应的数学模型，用数学的方法进行求解得出最优解。常规解析法常见的有线性规划法、动态优化法、序列算法、马儿可夫动态决策、模糊AHP、可行方向法等。

1970年，Matlin S[1]、1986年，Lloyd S P等[2]通过将分配问题按序排列，选取各火力单元的失败概率，使用最小失败概率进行优化选取目标与火力分配组合，该方法得到结果比较理想，但是算法的收敛慢、效率不高。

1977年，Nash[3]最早尝试解决有约束条件下资源优化配置问题。1993年，Libby V[4]通过大量计算采用线性规划研究火力分配问题，获得火力分配的最佳决策方法。2001年，Dasarathy B V[5]总结前人的基础上提出启发式近似法，试图减小线性规划的复杂计算问题，但是问题没有得到很好解决，精度也有待提高。

2004年，杨建兵等[6]结合层次分析法和线性规划法，分析坦克连冲击火力分配问题，最后使用软件以报告文件或图形的方式显示火力分配结果。

2006年，纪兵等[7]利用马尔可夫决策理论建立坦克连的动态火力分配模型, 使结果更符合战场动态环境情况的随机问题；2009年，陈伟兵等[8]将马尔可夫决策理论运用到炮兵群火力分配中，建立了炮兵群动态火力分配模型，通过例子验证该方法的可行性。

2007年，黄力伟等[9]针对目标函数是线性或非线性的一类火力分配问题, 提出了虚拟火力单位或目标的方法, 将问题转化为能够用匈牙利算法求解的指派问题, 该方法简单、易于计算, 有一定的应用价值。

2011年，王净等[10]基于动态规划算法对舰空导弹火力分配模型进行研究, 给出了动态规划的算法，得到最优火力分配结果。

2013年，丁红岩等[11]针对水面舰艇编队攻潜火力分配问题，运用模糊AHP 方法，通过构建攻潜火力分配模型，进而建立模糊评判矩阵，确定各个评价因素的权重，最后制定最优的火力分配方案。该方法可操作性较强，为反潜作战提供一定的辅助决策。同年，梁波等[12]考虑目标价值指标、武器对目标的单位毁伤概率以及目标防卫能力, 提出了基于可行方向法的火力分配模型。通过仿真实例验证模型及其算法有效。

2016年，谭乐祖等[13]考虑分析多目标规划模型的约束条件和目标函数基础上，建立多目标整数规划模型，求解火力分配问题。

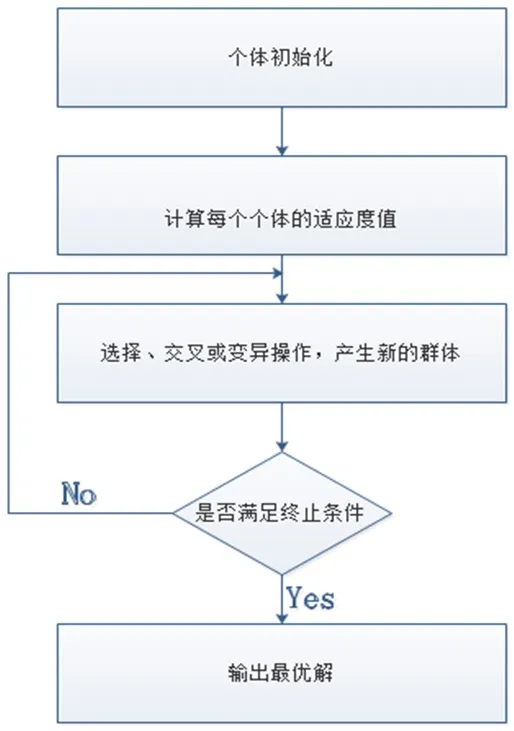
图1

常规解析火力分配法要求数学逻辑严谨、有明确的数学表达式，能够分析建立适当的数学模型，而且其庞大的计算量影响到计算的效率不高，在解决大规模火力分配问题时，问题更加突出，难以满足现代战争实时性的要求。

2 智能进化火力分配法

随着科学技术的不断发展，常规解析火力分配法的缺陷得到一定程度得到解决，智能进化算法的运用使得火力分配优化问题解决空间得到迅速扩展， 不断发展完善的优化算法通过计算机得以实现，这些智能的进化算法为解决复杂、非线性优化问题开辟了新的路径。其中常见的有粒子群算法、人工神经网络法、差分进化算法、遗传算法、禁忌搜索算法和影响网络[14]等。

智能进化算法是以模拟自然界生物进化过程的优化算法，出发点是模拟自然界生物群体生活时，个体之间的互相交流与合作，利用个体的简单、有限行为拓展到群体的、完成复杂任务的整体能力。如鸟群算法、蚁群算法、蜂群算法、粒子群算法、萤火虫算法等，以固体退火理论及系统稳定性理论为基础的模拟退火算法、Hop fi eld 神经优化算法，以及遗传算法、免疫算法、禁忌搜索算法等，都可以归结为智能进化算法。进化计算在发展的过程中形成了进化策略、进化编程和遗传算法三类主要的算法。这些算法都是基于种群的启发式算法，使用交叉算子、变异算子和选择算子搜索问题。进化算法的一般执行过程如图1所示。

不同的进化算法主要的区别在于编码形式和算子的执行方式不同。由于不同生物个体之间差异较大，个体的功能描述也千差万别，但在进化算法方面有其统一的框架模式，都是基于概率的随机搜索方式，各种不同算法在结构、内容和计算方法等方面具有较大的相似性。

1991年，Dorigo等[15]受到自然界蚂蚁觅食行为的启发，通过模拟蚂蚁觅食行为，提出了蚁群优化算法。

1995年，Kennedy J等[16]基于对鸟群捕食行为的研究第一次提出了粒子群优化算法,该算法具有操作、编程简单的特点。

2005年，余有明等[17]提出了多种群伪并行混沌遗传算法。结合多群体伪并行性和混沌运动随机性, 将混沌变尺度映射机理应用到种群优化进化。 一定程度提高了收敛速度和最优解搜索成功率。

2006年，丁铸等[18]将改进型微粒群算法运用到防空火力分配问题中，并和其他算法对比，该算法具有较快收敛性和较高收敛精度。同年，李丹等[19]基于神经网络TSP 算法解决防空作战火力分配问题。

2008年，陈华东等[20]使用混合粒子群算法的求解多平台多武器的火力分配问题, 该算法在规模复杂问题中体现算法的优越性。

2010年，傅调平等[21]提出基于自适应编码的遗传算法解决火力分配问题, 自适应选择、交叉和变异, 具有较快的收敛速度，较好地避免陷入局部最优。

2012年，隋永华等[22]提出了一种新的基于微分进化算法的求解方法。在分析基本微分进化算法的基础上，改进利用自由差分提高算法收敛速度，增设单体随机变异弥补种群多样性降低的缺陷，最后进行了遗传算法、基本微分进化算法对比测试，结果表明改进的微分进化算法更加有效；同年，韩占朋等[23]结合混合蛙跳算法对防空作战火力分配问题进行了研究，通过引入可变步长，使多点变异方式转换到单点变换方式进行改进混合蛙跳算法求解模型，取得较好的收敛速度和精度。

2016年，董朝阳等[24]提出一种改进遗传算法。通过构造改进的适应度函数，从而提高算法的收敛精度，通过计算染色体的相似度来选择交叉或变异操作，提高了算法的寻优性和效率。

智能进化火力分配法拓宽了火力分配问题的广度和深度，一定程度上提高了速度和精度，为现代复杂战场环境下的火力分配问题提供了新的研究思路和手段。

3 混合式火力分配法

混合式火力分配法是结合了常规解析火力分配法和智能进化火力分配法这两种方法，通过有效组合运用常规解析火力分配法和智能进化火力分配法，使得火力分配优化问题得到进一步完善的解决，该混合式火力分配法具有上述两种不具有的收敛速度较快、寻优能力强、鲁棒性强的优势，是目前解决火力分配优化问题的可靠方法，也是现阶段专家学者研究和关注较多的方法。常见的混合式火力分配法有如下。

2007年，马宏斌等[25]采用改进型遗传和蚁群混合算法对防空兵群火力分配问题进行研究，将蚁群算法的双向图引入改进型的遗传算法中，将武器分配优化转化为双向寻找最佳路径，避免陷入局部最优和提高了搜索效率；同年，丁铸等[26]结合禁忌搜索和微粒群优化算法，提出混合优化策略用于解决目标火力分配问题，提高了原算法的性能。

2008 年，程杰等[27]结合粒子群算法和遗传算法，将遗传算法中的变异操作引入粒子群算法中，增强全局搜索能力，有助于跨出局部最优。

2011年，曾松林等[28]基于动态博弈建立防空火力单元分配模型，利用双矩阵博弈纳什均衡建立纳什均衡二次规划，并利用混合粒子群算法进行求解，具有较高的应用价值。

2012年，孙媛等[29]提出了一种改进的混合遗传算法，将模拟退火算法与遗传算法相结合，引入小生境技术解决早熟问题，然后利用模拟退火算法解决陷入局部最优问题，使得问题得到较好的解决。

2013年，罗佳等[30]结合免疫遗传算法和量子遗传算法，利用免疫克隆、免疫记忆、免疫平衡算子改善优化量子遗传算法，引入先验知识和局部最优解来提高算法的收敛精度、收敛速度和稳定性。

2016年，周兴旺等[31]从博弈论的角度研究火力分配问题，建立基于贝叶斯混合博弈的火力分配模型。通过构造贝叶斯混合博弈树，利用混合粒子群算法求解，有效性好，有较高的理论应用价值。

4 MOEA/D进化算法

实践中大多数优化问题是多目标优化问题，需要在约束条件下同时考虑多个优化目标，且大多数目标并不是独立存在的，每个目标都有不同的意义和量纲，各个目标之间存在相互耦合、竞争的关系。传统求解多目标优化问题的方法是用权重系数将各个目标聚合为一个单目标，然后用单目标优化方法来求解。主要问题有：一是由于这些子目标往往相互冲突或关系未知，不存在或很难确定是否存在单个最优解使得多个目标同时获得最优，此时需要通过多次设置不同的权重来得到多个“最优解”来进行比较，这给求解多目标优化问题的求解带来了巨大的计算量；二是单个优化目标经过数学建模，具有相应的目标函数，而多目标函数往往高度非线性、不可微分和多极值，这给优化问题带来了极大的困难；三是各目标之间相互制约，对其中一目标优化必须牺牲其他目标为代价。

创伤性颅内损伤患者所用全身用抗感染药各亚类中，金额排序前3位的分别是第三代头孢菌素类药物（1 622.98万元）、碳青霉烯类药物（1 023.96万元）、第二代头孢菌素类药物（493.91万元）；DDDs排序前3位的分别是第三代头孢菌素类药物（94 635.5）、第二代头孢菌素类药物（28 962.6）、氟喹诺酮类药物（22 586.3），详见表7。

2007年，Zhang等[32]提出了一种新的多目标优化算法框架—MOEA/D。MOEA/D先将MOP分解为多个标量优化子问题；每个子问题通过交换各自解的信息来加快搜索速度。为了避免算法早熟，解信息的交换一般发生在临近子问题之间，而临近子问题通常通过聚合系数的欧式距离决定的，这是因为我们假设较近的聚合系数产生的子问题的最优解也较相近。每个子问题保留的解都是迄今为止对应聚合系数最好的解。可见，MOEA/D的基础是分解策略。

MOEA/D将MOP分解为多个标量优化子问题指的是：MOEA/D没有将MOP作为一个整体进行处理，而是将一个MOP分解为N个单目标优化问题，其中分解是通过聚合方法实现的。常见的聚合方法有：加权和方法、切比雪夫方法为例说明。

加权和（weighted sum）方法：

标量优化问题的最优解是一个Pareto最优解；而Pareto最优解可能是某个聚合标量优化问题的最优解。因此，PF的逼近可以转化为多个标量优化子问题。这也是很多传统数学规划法逼近PF的基本思想。可见，将MOP分解为多个标量优化问题是个很好的求解方法。

本文在借鉴国内外相关领域研究成果的基础上，尝试将火力分配的优化算法进行系统整合。从算法概念、模型理论和发展情况方面对火力分配的优化算法进行了初步研究，希望能借此开拓思路，为进一步研究航母编队反潜作战火力分配的应用打下理论基础。

[1]Matlin S.A Review of the Literature on the Missile-Allocation Problem[M]. INFORMS,1970.

[2]Lloyd S P,Witsenhausen H S.Weapons allocation is NP-complete[C].IEEE Summer Conference on Simulation. 1986.

[3]Nash J M.Optimal allocation of tracking resources[C].Decision and Control Including the,Symposium on Adaptive Processes and A Special Symposium on Fuzzy Set Theory and Applications,1977 IEEE Conference on.IEEE,1977：1177-1180.

[4]Libby V.Information-based sensor management[J].Proc Spie,1993,1955(1955)：156-164.

[5]Dasarathy B V.Distributed resource allocation under communication constraints[J].Proc Spie,2001：213-224.

[6]杨建兵,李大鹏,王忠义,杜涛.线性规划在最优火力分配辅助决策中的应用,2004(19)：550-560．

[7]纪兵,侯胜高,刘学银.基于马尔可夫决策过程的坦克连动态火力分配方法研究[J].火力与指挥控制,2008,31(07)：15-19.

[8]陈伟兵,蔡向阳,姜博轩.基于马尔可夫决策过程的炮兵群动态火力分配方法[J].国防科技,2009,30(04)：56-58．

[9]黄力伟,许品刚,王勤.基于匈牙利算法求解的火力分配问题[J].火力与指挥控制,2007,32(06)：25-28.

[10]王净,战凯,晏峰.基于动态规划算法的舰空导弹火力分配模型研究[J].舰船电子工程,2011,200(02)：24-26.

[11]丁红岩,董晓明,寇祝.基于模糊AHP的水面舰艇编队攻潜武器分配[J].指挥控制与仿真,2013,35(04)：138-142．

[12]梁波，段然基于可行方向法的火力分配模型[J].指挥信息系统与技术,2013,4(02)：30-32．

[13]谭乐祖,张 峥,孙仲元.多型反舰导弹混合攻击异型舰艇编队多目标整数规划火力分配模型[J].兵工自动化,2016,35(08)：47-49．

[14]孙清.基于影响网络和分布估计算法的空袭火力分配方法研究[D].国防科学技术大学,2011.

[15]L.M.Gambardella,E.Taillard,and G.Agazzi.MACS-VRPTW：A multiple ant colony system for vehicle routing problems with time windows.In D.Corne,M.Dorigo,F. Glover,D.Dasgupta,P.Moscato,R. Poli,and K.V.Price,editors,New Ideas in Optimization,McGraw-Hill,1999,pp.63-76.

[16]Kennedy J,Eberhart R.Particle swarm optimization[C].IEEE International Conference on Neural Networks,1995.Proceedings.IEEE Xplore,1995：1942-1948 vol.4.

[17]余有明,刘玉树,刘昆.混沌伪并行遗传算法及其在火力分配优化中的应用[J].北京理工大学学报,2005,25(12)：1047-1051．

[18]丁铸,马大为,张学锋,徐志强.基于改进微粒群算法的火力分配[J].弹箭与制导学报,2006：578-580．

[19]李丹,王巨海,陈振雷.基于神经网络TSP算法的防空作战火力分配[J].火力与指挥控制,2006,31(04)：42-45．

[20]陈华东,王树宗,王航宇.基于混合粒子群算法的多平台多武器火力分配研究[J].系统工程与电子技术,2008,30(05)：880-883．

[21]傅调平,陈建华,李刚强.基于动态自适应遗传算法的舰艇防空火力分配[J].广西师范大学学报：自然科学版,2010,28(03)：187-190．

[22]隋永华,郭雷,俞利新,王海晏.改进的微分进化算法求解空战火力分配问题[J].火力与指挥控制,2012,37(12)：118-121．

[23]韩占朋,王玉惠,姜长生,吴庆宪.用混合蛙跳算法的智能防空火力分配[J].电光与控制,2012,19(12)：10-13．

[24]董朝阳,路遥,王青.改进的遗传算法求解火力分配优化问题[J].兵工学报,2016,37(01)：97-102．

[25]马宏斌,王玉生.基于改进型遗传和蚁群混合算法的防空兵群火力分配模型[J].武器装备自动化,2007,26(07)：3-4.

[26]丁铸,马大为,于存贵,张学锋.基于禁忌搜索与微粒群优化算法的混合优化策略算法在目标分配问题上的应用[J].兵工学报,2007,28(09)：1127-1131．

[27]程杰,李勇,任伟.改进粒子群算法在防空火力分配中的应用[J].武器装备自动化,2008,27(04)：10-11．

[28]曾松林,王文恽,丁大春,张毅.基于动态博弈的目标分配方法研究[J].电光与控制,2011,18(02)：26-29．

[297]孙媛,王毅,李季颖.改进的混合遗传算法在防空目标分配中的应用[J].四川兵工学报,2012,33(09)：113-116．

[30]罗佳,薛青,王之腾,张宏军.作战仿真中火力分配优化算法研究[J].计算机仿真,2013,30(10)：62-66．

[31]周兴旺,从福仲,庞世春,侯满义,辛腾达.基于贝叶斯混合博弈的空袭火力资源分配决策模型[J].火力与指挥控制,2016,41(07)：18-22．

[32]Zhang Q,Li H. 2007.MOEA/D：A multiobjective evolutionary algorithm based on decomposition[J].IEEE Trans Evol Comput,11(06)：712-731.

作者单位
1.国防大学研究生院 北京市 100091
2.国防大学公共平台中心 北京市 100091

陈龙（1988-），男，福建省仙游县人。硕士在读，现为国防大学研究生。主要研究方向为作战模拟系统工程。