极限风况下不同基础形式的风电机组塔架荷载估计

文|许楠

极限风况下不同基础形式的风电机组塔架荷载估计

文|许楠

目前，从陆上风电机组到海上风电机组，随着离岸距离和水深的增加，基础形式分为陆上的固定式，近海的底部固定式和浮体式。以往研究大都只针对某一种基础结构形式来研究塔架的荷载。研究表明，不同的基础形式会产生不同的塔架荷载，对于浮体式风电机组，数值模拟是常用的荷载评估方法，鉴于固定基础模型不适用于计算浮体式风电机组的塔架荷载，因此有必要构建一种通用的荷载计算模型，从而可以运用解析公式来估计极限风况下的塔架荷载。本文提出了SR （Sway-Rocking） 模型作为任意基础形式的风电机组通用的荷载计算模型。SR模型可将复杂的浮体式风力发电机组的锚固体系简化为一个横向的弹簧及阻尼器和一个转动的弹簧及阻尼器，两个弹簧的刚度和两个阻尼器的阻尼可以通过FEM （Finite Element Model） 分析来获取。通过改变弹簧刚度和阻尼器阻尼可以模拟不同的基础形式风电机组的塔架荷载，从而可以利用等效静力荷载方法和模态分析来推导极限风况下塔架荷载的理论计算公式。对于每一种基础形式，理论公式均已由动力响应分析验证。

风电机组、基础与锚固体系

本文研究风荷载的模型选取半潜式浮体作为基础，锚固体系分别采用张力腿和悬链线体系，浮体之上安装NREL 5MW型号风电机组。浮体的详细参数参见表1：张力腿锚固体系，考虑到尽量消减浮体的纵摇效应，3条张力索分别连接浮体的3个角柱，参照图1（a）；悬链线锚固体系由3条400m跨度的锚链共同连接在中心柱的底端，相邻锚链水平投影的夹角为120°，其中一条沿入射波的方向伸展，参照图1（b）；风电机组的详细参数参见表2。本文采用FEM计算程序来验证塔架荷载的解析公式，程序可以考虑风电机组、浮体及锚固体系之间的耦合特性。

表1 半潜式浮体的参数

表2 NREL 5MW风电机组的参数

图1 本文研究的锚固体系

SR（Sway-Rocking）模型

纵移和纵摇是浮体6个自由度运动（如图2）中最为显著的两个，其他方向的运动可以忽略。因此，本研究借鉴地震工程中常用的SR模型（如图3）作为等效计算模型模拟浮体运动对塔架荷载的影响。SR模型可将复杂的锚固体系简化为两个方向的弹簧和阻尼器：纵移用一个横向的弹簧和阻尼器模拟，纵摇用一个转动的弹簧和阻尼器模拟。与地震工程不同的是等效刚度kS， kR和阻尼cS， cR需通过FEM分析来获取。

采用完整的浮体风电机组体系模型，将上部结构（风电机组和浮体）视为刚体，横向频率ωS和转动频率ωR可以通过FEM数值模拟体系的自由振动获得。因此，两个弹簧的刚度可按下式计算：

式中，m是风电机组和浮体的总质量， m(r)是r位置处的单位长度质量，h(r)是距离塔架底部的高度。 由于浮体被看作是塔架底部的集中质量，不考虑其尺寸的影响，因此公式（2）中仅在风电机组部分做积分。另外，两个阻尼器的阻尼也可以由FEM数值模拟进行估计。将上部结构的多自由度体系简化为等效单自由度模型，同时考虑了横向和转动运动，通常被称作压缩SR模型（图4）。单自由度体系的质量，刚度，阻尼比分别为me，ke，ce。

由于第一阶振动模态对风电机组塔架的风荷载贡献最为显著，而高阶频率在风荷载谱中所占的能量非常小，所以本研究忽略高阶模态的影响，只考虑第一阶模态。图4的压缩SR模型的第一阶固有周期T1可以由固定基础模型的第一阶固有周期Tf，横向固有周期TS和转动固有周期TR计算，如公式（3）所示。

要计算压缩SR模型的阻尼比，需考虑一个循环振动周期T1内的应变能E和吸收的能量ΔE，则第一阶模态的阻尼比ξ1推导如下：

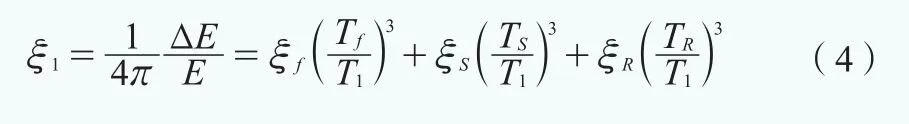
式中，ξf是固定基础模型的第一阶阻尼比，ξs是横向阻尼比，ξR是转动阻尼比。计算SR模型的第一阶固有周期T1和阻尼比ξ1的必要参数见表3。

图2 浮体式风电机组体系的运动

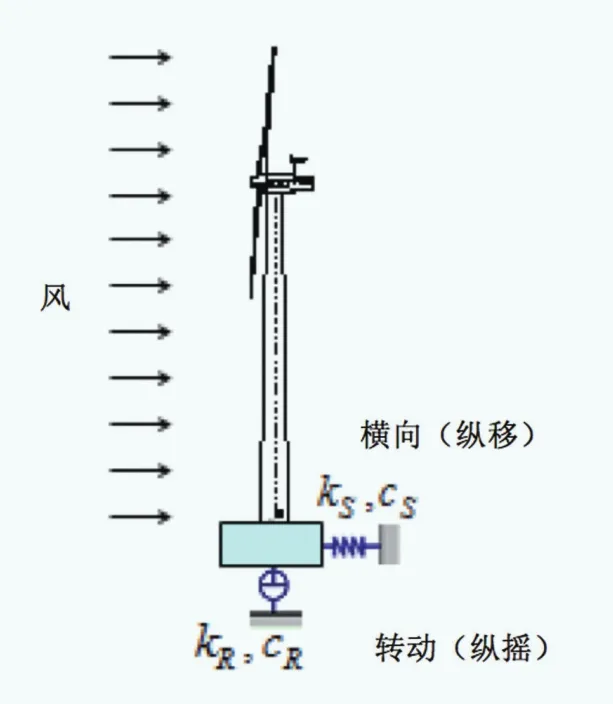
图3 Sway-Rocking 模型

图4 压缩SR模型

表3 周期和阻尼比

风荷载估计

与固定式基础的风电机组一样，作用在塔架上的最大风荷载依然可采用等效静风荷载公式计算，其中平均风荷载的计算也与固定式基础无差异。由于平均风荷载依赖于风本身，所以在相同风况下，不同基础形式的塔架平均风荷载是相同的。标准差也同样包含了背景部分σB和共振部分σR：

式中，Iuh为轮毂高度处的湍流强度，Q为平均风荷载，φ为振型修正系数，Ruh（n1）为标准化的功率谱密度，KB和 KR（n1）分别为背景和共振分量的尺寸折减系数，n1为塔架的第一阶固有频率，ξ为阻尼比。KB可按下式计算：

式中R为风轮半径，Lu为湍流积分尺度。因此，与平均风荷载一样，不同基础形式的背景标准差是相同的，因为它只依赖于风本身和风电机组尺寸。但是共振分量是ϕ，Ruh（n1），KR（n1）和ξ的函数，因此除了风本身它还和结构自身的振动特性有关，所以会随着基础形式而发生变化。振型修正系数ϕ与振型和模态质量有关，从图5可以看出 ，固定基础模型的振型修正系数比SR模型的稍低，但并不显著。

标准化的风速谱Ruh（n1）和共振分量的尺寸折减系数KR（n1）以及阻尼比ξ表示如下：

式中Uh为轮毂高度处的平均风速，C为无量纲的衰减因子，ξ1为系统的阻尼比，ξa为气动阻尼比。

图6和图7给出了标准化风速谱Ruh（n1）和共振分量的尺寸折减系数KR（n1）随第一阶固有频率的变化。从图中可以看出，由于固定基础模型的固有频率值比SR模型高，所以其Ruh（n1）和KR（n1）的值要比SR模型低很多。因此，对于浮体式风电机组如采用固定基础模型，会低估其共振标准差。

图5 振型修正系数φ的比较

图6 标准化风速谱的比较

图7 共振分量的尺寸折减系数的比较

图8 总的阻尼比ξ的比较

由于不同基础形式的风电机组的气动阻尼比是相当的，这样差异较大的系统阻尼比会导致不同基础形式的总的阻尼比的差异较大。从图中可以看出，固定基础模型的总阻尼比要比SR模型的低很多，这就造成了采用固定基础模型会高估浮体式风电机组的共振标准差。

图9 标准差的比较

图10 峰值因子的比较

以上分析可以看出，第一阶固有频率和系统阻尼比是估计塔架荷载的两大控制因素，而固定基础模型在这两个因素上与SR模型有着较大差异，所以固定基础模型不能用来计算浮体式风电机组体系的风荷载。如图9所示，对于不同的基础形式，利用SR模型提出的计算公式都可以给出与数值模拟接近的结果。另外，悬链线体系风电机组的标准差比张力腿体系的低，也是由于其较大的阻尼比引起的（图8）。

塔架荷载的非高斯峰值因子是向上零穿越概率以及偏度的函数。对于不同的基础形式，偏度无较大差异，而且由于海上的低湍流度，偏度值很低；向上零穿越概率受第一阶固有频率影响较大，所以固定基础模型和SR模型的向上零穿越概率差异较大。图10给出了峰值因子随向上零穿越概率的变化，可以看出峰值因子随向上零穿越概率变化不大。因此，两种模型有着接近的峰值因子。

结论

本文提出了SR模型作为任意基础形式的风电机组的通用荷载计算模型。SR模型可以考虑浮体运动对塔架荷载的影响，通过改变弹簧刚度和阻尼器阻尼可以模拟不同的基础形式的塔架荷载，从而利用等效静力荷载方法和模态分析推导了极限风况下塔架上的风荷载的理论计算公式。本文比较了固定式基础和浮体式基础（张力腿和悬链线）的风电机组塔架上的风荷载。由理论公式可以看出，对于不同的基础形式平均风荷载和标准差的背景分量是相同的，这是因为它们是由风本身决定的；但是标准差的共振分量是不同的，因为它还依赖于结构自身的振动特性。研究发现，第一阶固有频率和系统阻尼比是估计塔架荷载的两大控制因素，而固定基础模型在这两个因素上与SR模型有着较大差异，所以传统的固定基础模型只能用于陆上风电机组，而SR模型适用于任意基础形式的风电机组。本研究还发现非高斯峰值因子对基础类型不敏感。

（作者单位：中国广核新能源控股有限公司）