基于有限穿越水平可视图的短时睡眠心率变异性研究∗

霍铖宇马小飞 宁新宝

1)(常熟理工学院物理与电子工程学院,常熟 215500)

2)(南京大学电子科学与工程学院,生物医学电子工程研究所,南京 210023)

基于有限穿越水平可视图的短时睡眠心率变异性研究∗

霍铖宇1)†马小飞2)宁新宝2)

1)(常熟理工学院物理与电子工程学院,常熟 215500)

2)(南京大学电子科学与工程学院,生物医学电子工程研究所,南京 210023)

(2017年4月10日收到;2017年6月7日收到修改稿)

心率数据是最易于获取的人体生理数据之一,基于心率变异性的睡眠分析是近年来各种用于日常健康管理的可穿戴设备功能的一个重要发展方向,需要不断探索可以应用于标准睡眠分期时间窗(约30 s)的各类短时特征参数.利用近期报道的有限穿越水平可视图,并进一步提出一种加权有限穿越水平可视图,将不同睡眠状态下的短时心率变异序列映射为网络,进而提取平均集聚系数、特征路径长度、集聚系数熵、路径分布熵、加权集聚系数熵和加权路径分布熵等网络特征参数进行统计分析.结果表明,各网络参数值在醒觉、浅睡期、深睡期和快速眼动期的幅度水平具有显著差异,体现了所述方法在基于短时心率变异数据的睡眠分期中的有效性.同时,进一步研究了健康年轻人和中老年人在不同睡眠状态下的网络参数值,发现两者虽然存在整体的水平差异,但是在不同睡眠状态间的变化仍具有相同的趋势,反映出相对于正常的年龄老化,睡眠调制对心脏动力学系统具有更显著的影响,也说明所述方法可作为基于心率变异性的睡眠研究的一种新的辅助工具.

有限穿越水平可视图,睡眠,心率变异性

1 引 言

睡眠是一种重要的生理活动,对于人体的物理和精神方面的自我恢复具有非常关键的作用[1].根据美国睡眠医学学会(American Academy of Sleep Medicine,AASM)发布的规范,睡眠过程可以进行分期,具体分为醒觉(wakefu lness,W),非快速眼动期(non-rapid eyemovement,NREM)和快速眼动期(rapid eyemovement,REM).其中,NREM阶段根据不同脑电特征所体现的睡眠深度又可分为N1,N2,N3三个阶段[2].在一些研究中,通常将N1和N2阶段统称为浅睡眠(light sleep,LS),而N3阶段被称为深睡眠(deep sleep,DS)或慢波睡眠(sloWwave sleep,SWS)[3,4].在早期的睡眠分期标准(Rechtschaffen and Kales Standard,R&K Standard)中,浅睡眠分为S1和S2两个阶段,深睡眠还依据脑电中δ波的比例进一步划分为S3和S4两个阶段[5,6].准确的睡眠分期对于睡眠质量的评估及睡眠相关疾病的诊断都具有重要的意义.目前用于睡眠分期的金标准是以脑电为基础的多导睡眠图(polysomnography,PSG)监测,通常需要在医院专门的睡眠实验室中进行,费用高,设备复杂,在病人身上放置的电极较多,需要专业操作,给病人带来的生理心理负荷大,常常会干扰其正常睡眠.对于普通人群,更适合的睡眠评估监测手段是便携化、低成本、不影响睡眠的非专业级设备,相应的信号来源也以方便采集的非脑电信号为主.以往研究证实,心率变异性(heart rate variability,HRV)和人体自主神经的活动密切相关,与睡眠也有着密切的联系[7],在不同的睡眠期,相应的HRV序列具有不同的信号特征,因此HRV也是获得睡眠信息的重要途径[8−10].相应地,各类基于线性和非线性方法的睡眠状态HRV特征参数的提取也得到了较为广泛的研究[11].但是,许多基于HRV的睡眠状态分析往往采用相对较长的时间窗(例如5 Min左右)[12−14],这与睡眠分期规范中30 s时长的分期基本单位并不符合.因此,从30 s左右的短时HRV序列中寻找有效的睡眠特征参数,仍然有着重要的意义和价值[15].

近年来,复杂网络的相关理论已开始广泛应用于生理信号的分析[16−19].以往的研究表明,一种有效的探测HRV序列动力学特性的方法是把序列转换成复杂网络[20−23].Lacasa等[24]提出的可视图(visibility graph,VG)方法,是近年来得到广泛应用的一种比较典型的转换方法.VG方法构建的网络能够保留时间序列的一些内在信息和特征,周期序列被映射为规则网络,随机序列被映射为随机网络,而具有分形自相似特性的序列则被映射为无标度网络.经仿射变换或坐标轴尺度变换后其可视性不变.Liu等[25]将VG方法作为一种特征提取手段应用于脑电信号的睡眠分期;Long等[3]将VG方法应用于睡眠过程心跳呼吸耦合序列分析;Hou等[26]将VG方法应用于短时HRV序列的睡眠特征分析,所采用的几个复杂网络参数的计算结果在不同睡眠阶段体现出了一定的统计学差异,同时也观察到了由HRV序列映射得到的可视图的幂律形式的度分布,并且其平均路径长度与节点数之间的关系体现了“小世界网络”的特性.

在标准VG的基础上,Luque等[27]又提出了一种水平可视图(horizontal visibility graph,HVG),该方法与VG方法具有一些相同的性质,如节点至少和左右相邻点相连接,为无向网络,坐标尺度变换或仿射变换后可视性不变等.HVG方法能够反映随机序列和混沌序列的差异,比VG的可视性准则更严格而简单,不再需要进行直线的插值计算,进一步提高了映射运算的效率,近年来在时间序列的分析中也得到了广泛的应用,并相继有研究者对其提出了各种改进,如加权的水平可视图[28]、有限穿越水平可视图等[29],并在气液两相流、脑电等时间序列的分析中获得了较好的效果.因此,本文考虑基于改进的HVG相关方法,对不同睡眠状态的短时HRV数据进行分析,以期在相对标准VG进一步提高计算效率的前提下,获得相类似或更有效的分析结果,从而为基于短时HRV数据的睡眠生理研究提供新的手段和途径.

2 方 法

2.1 有限穿越水平可视图

有限穿越水平可视图(liMiMtied penetrable horizontal visibility graph,LPHVG)[29]是标准HVG的一个扩展.其基本思想是:首先定义有限穿越视距Lp,然后将原始时间序列中的点定义为网络节点,根据其幅度绘出相应高度的直方条.基于HVG方法可视性准则,两个节点存在连接的条件是在两个直方条之间绘出一条水平的可视线,且被位于两者之间的其他直方条截断的次数n≤Lp.图1为一个长度N=10的HRV序列在有限穿越视距Lp=1情况下基于LPHVG方法映射生成网络的示意图.图1(a)中双向实线箭头表示基于标准HVG方法的可视线,双向虚线箭头表示在有限穿越视距Lp=1情况下新增的可视线.图1(b)则是据此生成的网络图,其中实线和虚线的含义与图1(a)相同.

研究认为,在噪声的干扰下,HVG网络中本应相连的节点容易受到噪声点隔断,对建网效果产生影响,动力学特性被噪声掩盖[30,31].而LPHVG则具有相对更强的连接性,进而在较小的时间尺度上具备一定的抗噪性能,同时不影响对序列长程波动趋势的反映.

在构建网络的基础上,我们对四个复杂网络参数进行考察,分别为:平均集聚系数C、特征路径长度L、集聚系数熵Ec和路径分布熵Ed.

平均集聚系数C由Watts等在对“小世界网络”的研究中引入,其定义为[32]

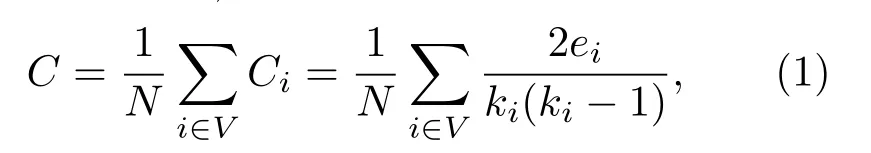
式中,V为所构造的图的节点集合,其中包含N个节点;与节点i相连的节点数为ki,所有与节点i相连的节点之间实际所连的边数为ei,其与这些节点之间可能连出的最大边数ki(ki−1)/2的比值即为节点i的局部集聚系数Ci,反映了图中的节点之间聚集成簇的程度.平均集聚系数C是图中所有顶点的局部集聚系数的算术平均值.

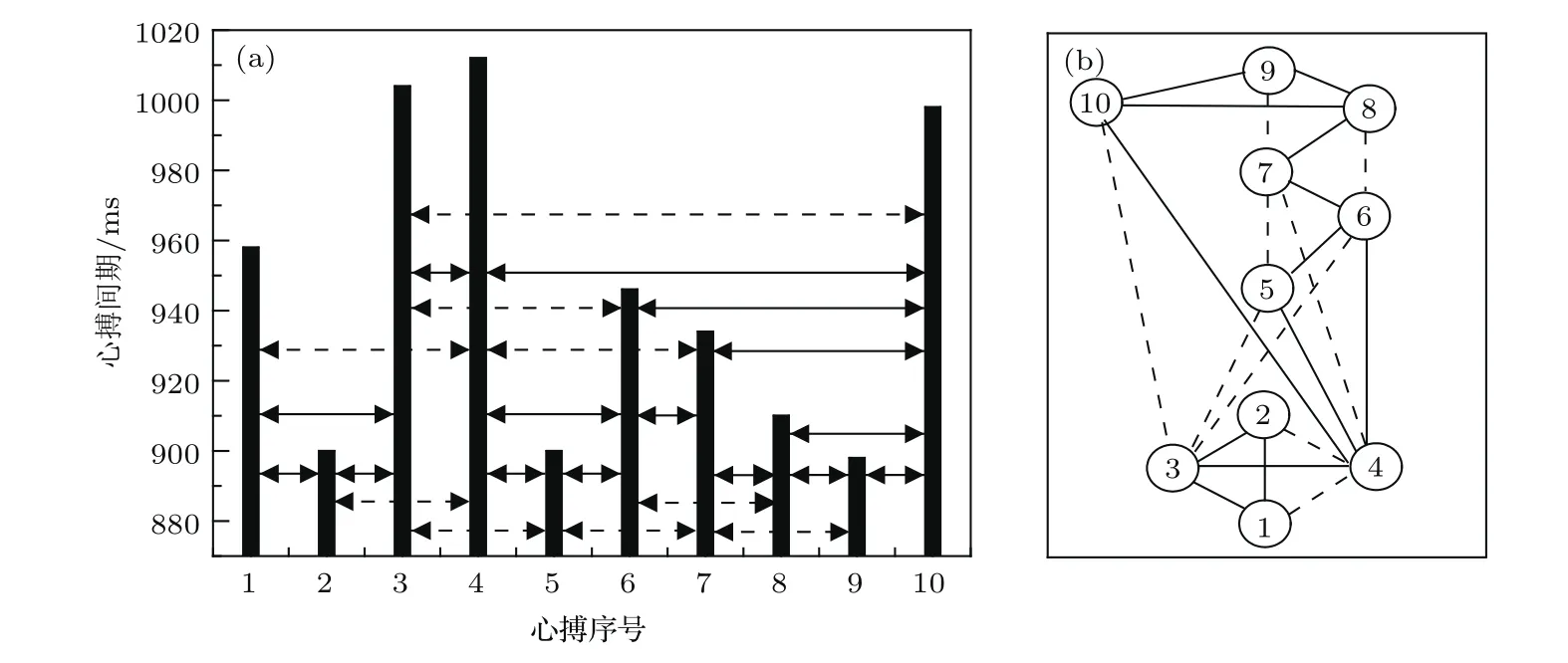
图1 有限穿越水平可视图网络构建示例(有限穿越视距Lp=1) (a)节点可视性示意图;(b)对应的网络图Fig.1.ExaMp le of the construction of a liMited penetrab le horizontal visibility graph(liMited penetrab le d istance Lp=1):(a)Illustration of visibility criteria based on a heartbeat interval tiMe series;(b)the correspond ing graph ex tracted froMtiMe series in(a)using the LPHVG algorithm.

特征路径长度L用于衡量图中两个节点之间的典型距离,其定义为[32]

式中,V为所构造的图的节点集合,N为图中包含的节点数,dij为节点i和j之间的最短路径长度.图中所有节点对之间的最短路径长度的平均值,即为特征路径长度.

集聚系数熵Ec的定义来自于对各节点的集聚系数分布情况的描述.首先计算各节点i的集聚系数Ci的分布频率PC,i,有

路径分布熵Ed用于描述各节点间路径的分布情况.首先对任意两个节点间的路径长度d的分布进行直方图统计[28](d的分布范围是[1,N−1],N为节点数),并得到不同路径长度d的分布频率Pd,据此定义路径分布熵Ed为

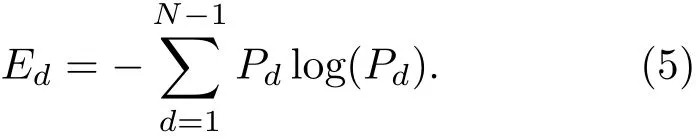
2.2 加权有限穿越水平可视图

在上一节所述的LPHVG基础上,我们进一步提出一种加权有限穿越水平可视图(weighted liMited penetrable horizontal visibility graph,WLPHVG)的构造方法.与前述LPHVG方法相同,定义有限穿越视距Lp并判断两个节点之间的连接性.同时,设两个节点i和j的幅度值分别为xi和xj,进一步定义两节点i和j之间的边的权值Wij为[34]

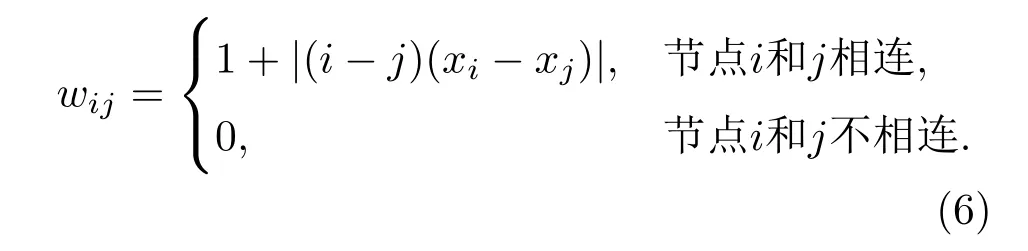
在将时间序列映射为加权网络的基础上,经综合考察,提取两个网络特征参数进行分析,分别为加权集聚系数熵ECw和权值分布熵Ew.

对于加权集聚系数熵,首先定义网络中节点i的加权集聚系数Cw,i为[35]

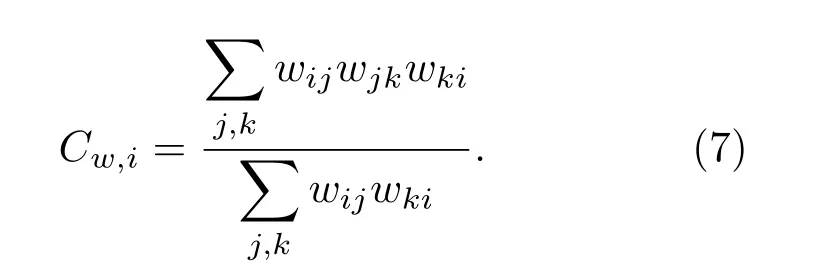
然后计算各节点i加权集聚系数Cw,i的分布频率P Cw,i,

最后,定义加权集聚系数熵ECw为

对于权值分布熵,首先对图中各条边的权值分布范围进行直方图统计(设划分区间数为M),并计算各权值区间内的边数分布频率[28].设第i个权值区间内的边数分布率为Pw,i,则权值分布熵Ew定义为

3 实验结果

3.1 数据来源及预处理

本文采用的数据来源于Sleep Heart Rate and Stroke VoluMe Data Bank[36],具体采用了该数据库中包含的45个健康人窦性心律RR间期数据集(RR normal sinus rhythm),该组数据来源于具有窦性心律的健康人的睡眠过程.在各数据记录对应的标识文件中,包含有数字组成的代码组合,用于区分不同的睡眠周期、睡眠分期状态(该数据库中的非快速眼动(NREM)睡眠是根据R&K标准分为S1—S4四个阶段)、是否为平稳数据等.对每个数据,本文根据标识文件的对应信息,在数据文件中截取具有连续30点长度(约30 s)且处于同一个睡眠分期状态的平稳的RR间期短数据段作为分析对象.总共获取的各睡眠状态下数据段数量如表1所列,其中,LS代表浅睡期(睡眠阶段S1和S2),DS代表深睡期(睡眠阶段S3和S4),REM代表快速眼动期,W代表醒觉状态.

表1 各睡眠状态数据段数量统计Tab le 1.Statistics of the nuMber of segMents in each sleep stage.

3.2 结果与讨论

采用第2部分所述的基于LPHVG及WLPHVG的方法,对四个不同睡眠状态下的HRV数据组进行了分析计算,在有限穿越视距Lp=1时,对应的6个网络参数测度值的柱状图分布如图2所示,图中柱状图高度表示参数均值,误差棒表示标准误.

作为比较,我们也基于标准VG方法构建无向图并计算了相同的4个网络参数,结果如图3所示.

由于计算结果的方差不齐,我们采用K ruskal-Wallis(KW)非参数检验方法对分析结果进行统计检验.零假设为:不同的睡眠/醒觉状态组的网络测度值来自于相同的分布.对图2中分析结果的统计检验显示,所有网络参数的KW检验的p＜1×10−200≪0.01,故拒绝零假设,可以认为不同的睡眠/醒觉状态组的网络测度值总体水平不全相同.为进一步分析各睡眠/醒觉状态之间两两是否存在差异,同时基于Tukey-K ramer方法进行了组间的多重比较,结果显示,对上述各参数而言,任意两个状态间的检验结果均满足p≪0.01,拒绝组间均值相等的零假设,说明上述6个参数的计算结果对于不同的睡眠/醒觉状态均存在显著差异.

关于构建网络时的有限穿越视距Lp,考虑到分析对象为短时数据,穿越视距过大会造成细节丢失,所以我们主要对三个不同的有限穿越视距Lp=0,Lp=1和Lp=2进行了分析测试.分析结果的柱状图基本模式是类似的,统计检验也均显示不同睡眠/醒觉状态的网络测度值总体水平不同.但是从组间多重比较结果来看,效果略有差异,例如当Lp=0(即原始的HVG)时,平均集聚系数C对于REM状态和W状态间的差异不显著.综合考察结果发现,穿越视距Lp=1下效果相对最好,可以认为在抗噪声能力和序列动力学特性探测能力方面达到了较好的平衡.

另外,与图2结果相比,对于标准VG分析(即图3中的结果),统计检验显示,所有网络参数的KW检验均满足p≪0.01,反映不同的睡眠/醒觉状态组的网络测度值总体水平不完全相同.但是在后续的组间多重比较中发现,部分睡眠状态间的差异不够显著,图3中标记为n.s.的即为统计检验无显著差异(p＞0.05)的睡眠状态组.总体而言,本文采用的分析方法,与标准VG相比,在短时HRV序列的睡眠状态分析这一应用场景中可以认为具有更优的效果,且计算速度更快.

以下对图2中的分析结果做进一步的探讨.从计算结果的柱状图上看,对于4个LPHVG网络下的特征参数,除了平均集聚系数C以外,其余3个参数在不同睡眠/醒觉状态均呈现相类似的变化规律.平均集聚系数C在REM状态下具有最小值,而在DS状态具有最大值;特征路径长度L及两个熵测度则相反,在REM状态及W状态的平均值较高,随着睡眠从LS向DS状态的加深,其值也逐渐下降.另两个WLPHVG参数各状态之间的变化规律与无权网络下的L,Ec和Ed相反,从醒觉W到浅睡LS再到深睡DS的变化趋势是逐渐增大,REM状态则反向变化.

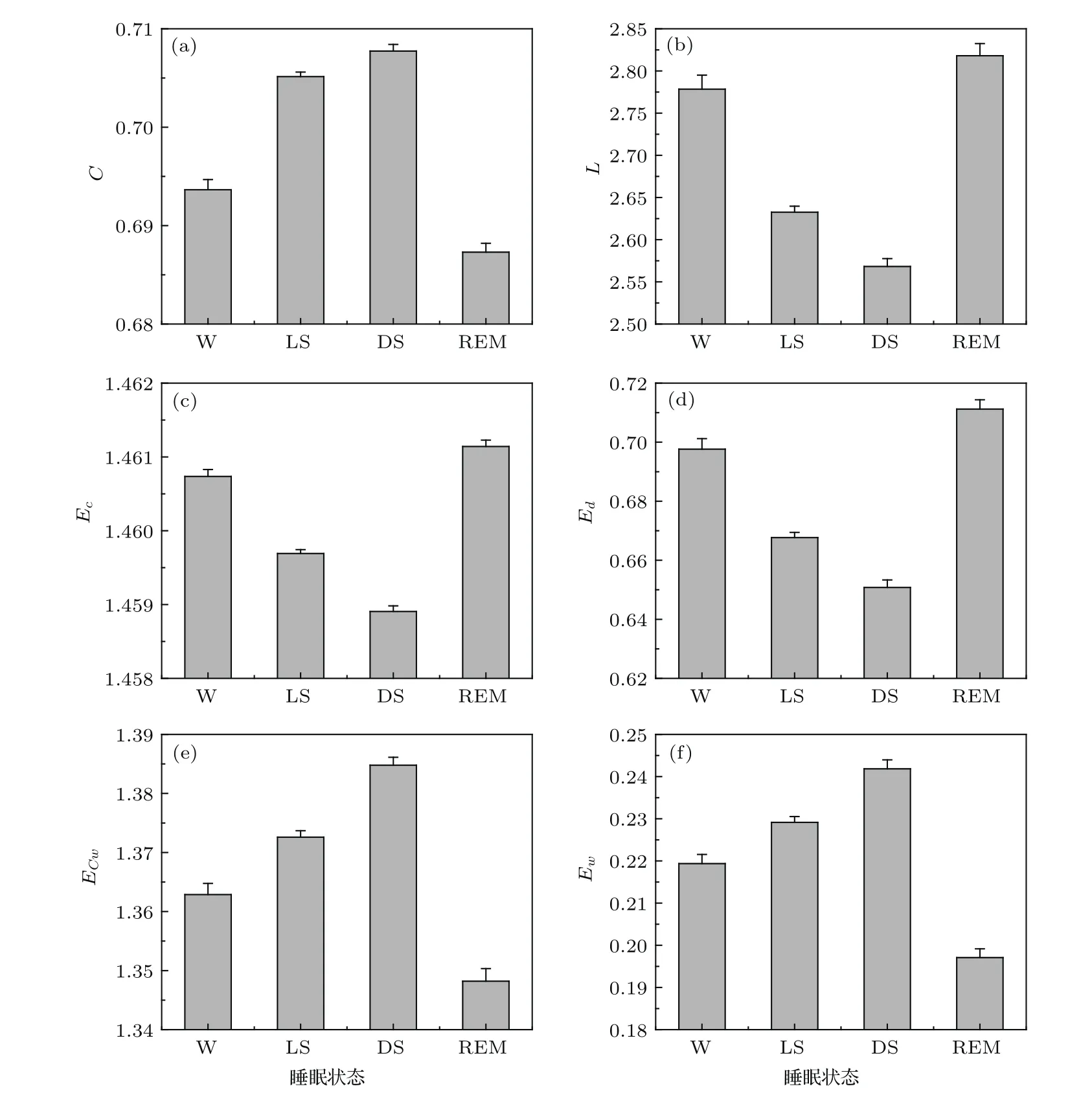
图2 睡眠HRV数据的LPHVG和WLPHVG网络参数计算结果 (a)平均集聚系数C;(b)特征路径长度L;(c)集聚系数熵Ec;(d)路径分布熵Ed;(e)加权集聚系数熵ECw;(f)权值分布熵EwFig.2.Network paraMeters calcu lated froMsleep HRV series using LPHVG and WLPHVG algorithm:(a)Average clustering coeffi cient C;(b)characteristic path length L;(c)clustering coeffi cient entropy Ec;(d)distance d istribu tion entropy Ed;(e)weighted clustering coeffi cient entropy ECw;(f)weight distribution entropy Ew.

心脏动力学系统是一个处于自主神经系统调控下的集成的生理系统输出的典型例子,因此,睡眠状态变化对心脏动力学系统输出的HRV序列所构成的网络参数的影响,来源于自主神经调控在不同睡眠状态下的变化,其相互关系比较复杂,受到很多因素的影响[37].事实上,自主神经调控的变化可以深刻影响睡眠发生和睡眠稳态,在睡眠过程中,随着不同睡眠阶段的变化(醒觉W、浅睡期LS、深睡期DS和快速眼动期REM),自主神经调控在交感神经系统和副交感神经系统的交替支配中波动[38].从醒觉状态到非快速眼动(NREM)状态的睡眠,与逐渐增长的副交感神经调制及逐渐下降的交感神经调制相联系,在NREM睡眠期间,随着从浅睡到深睡的睡眠程度的加深,心率等参数均逐渐下降,而HRV则有所上升;与之相反,从NREM阶段到REM睡眠阶段,HRV会有显著的降低,伴随着交感迷走神经平衡的变化,向着迷走神经控制减弱及交感神经调制增强的方向变化[39,40].在REM睡眠阶段,心血管系统呈现某种“激活”状态,其活动水平甚至会高于醒觉状态[37],因此从NREM到REM状态往往伴随着非常显著的参数变化.

结合图2的分析结果,从W到LS再到DS状态,各参数值的变化是向同一个方向逐渐加深(递增或递减),到DS状态时达到极大值或极小值,而从DS到REM状态,参数值则会发生反方向的显著变化,其差异甚至会大于DS和W状态的差异.这与上面提到的睡眠阶段变化中的自主神经调制过程的变化规律是相符合的.

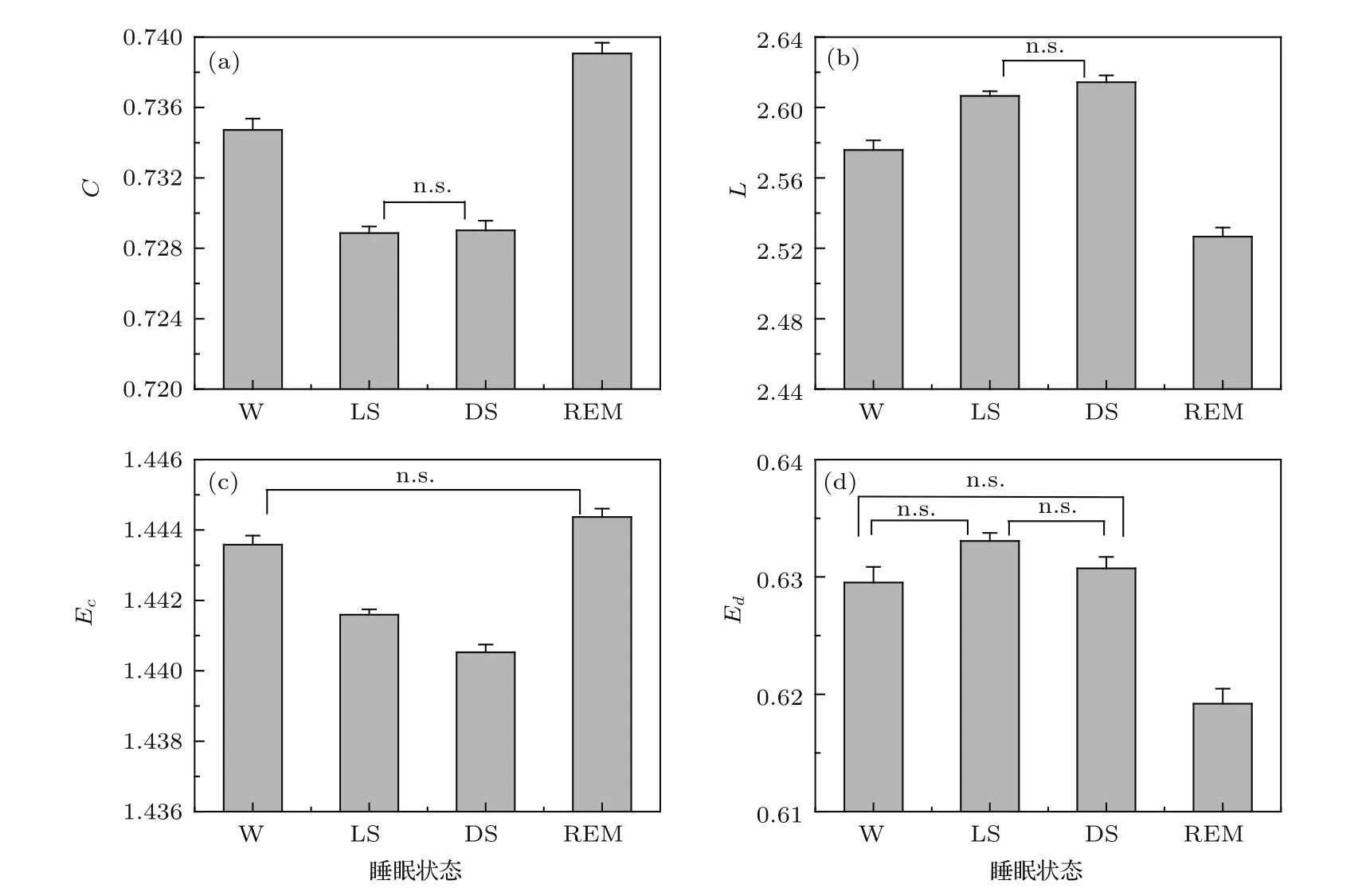
图3 睡眠HRV数据的标准VG网络参数计算结果 (a)平均集聚系数C;(b)特征路径长度L;(c)集聚系数熵Ec;(d)路径分布熵EdFig.3.Network paraMeters calcu lated froMsleep HRV series using standard VG algorithm:(a)Average clustering coeffi cient C;(b)characteristic path length L;(c)clustering coeffi cient entropy Ec;(d)distance d istribu tion entropy Ed.

总体而言,HRV序列作为复杂的自主神经调控过程的输出,具有高度的复杂性,在不同的睡眠阶段,序列的动力学特性必然存在差异.通过LPHVG和WLPHVG方法构建的网络,其网络参数值较为敏感地捕捉到了不同睡眠阶段HRV序列动力学特性的差异,并且与现有的生理学认知相符合.

此外,以前的研究表明,年龄的老化通常与生理功能的衰退和生理复杂性的降低相联系.睡眠的动态过程也被发现随着年龄老化而改变,例如,老年人通常会表现出更多的片段睡眠及更为频繁的唤醒以及深度睡眠持续时间的减少[41,42].在睡眠调控和心脏调控之间所存在的复杂交互机制,以及这种交互机制是否随着年龄老化会减弱,也是值得研究的问题.有一种观点认为,在不同的睡眠状态下,对于健康的中老年人,其HRV序列的有关测度仍会像年轻人一样有显著的差异;另一种观点则认为,由于与年龄相关的心脏系统的变异性和睡眠过程中自主神经调控响应能力的下降,对于健康的中老年人,其HRV序列的测度在不同睡眠状态下的差别将会变得不明显.

因此,我们将前文所述的LPHVG和WLPHVG方法应用于不同年龄组的HRV数据,对这一问题进行研究.数据仍然来源于3.1节中所介绍的数据库.在其中选取了10名年龄在25岁以下的健康年轻人样本(年龄为20.4±2.8岁,均值±SD)和10名年龄在45岁以上的健康中老年样本(年龄为50.2±4.8岁,均值±SD).由于前述的网络参数较多,为精简叙述,从LPHVG和WLPHVG两种方法构建的网络中各选取一个相对应的参数,即集聚系数熵Ec以及加权集聚系数熵ECw进行分析,结果如图4所示.

图4中,空心正方形及实心圆形标记表示计算结果的均值,误差棒表示标准误.紧靠标记上方或下方的字母组合表示该年龄组不同睡眠状态间的多重比较结果,若与某个睡眠状态有显著差异,则标记该状态的首字母.例如,图4(a)中年轻人的W状态,经统计检验,与LS,DS,REM状态均有显著差异,则标记为LDR,其余以此类推.

由图4可见,年轻人和中老年人的分析结果在参数值上存在一定的整体差异.图4(a)中,除醒觉状态外,中老年组的各睡眠状态参数值Ec显著高于年轻人组(Mann-Whitney-Wilcoxon TEST,p＜0.05);在图4(b)中,中老年组的各睡眠状态参数值ECw则显著低于年轻人组(Mann-Whitney-Wilcoxon TEST,p＜0.05).年轻人和中老年人整体参数值大小关系的不一致性主要来源于网络构建方法的差异,LPHVG和本文定义的WLPHVG方法实际上是从不同的角度反映了时间序列的性质,相应的网络参数在数值上并不具有直接的可比性.值得注意的是,这两种不同的网络构建方法所对应的网络参数都反映出随着年龄的老化,中老年人的生理机能尤其是心脏自主神经系统在睡眠过程中的调制作用确实相对年轻人发生了一定的改变.然而,从不同睡眠状态下参数值的变化趋势来看,无论是年轻人还是中老年人,其趋势是非常相似的.年轻人和中老年人在不同睡眠状态下的参数值均呈现相类似且较为显著的变化趋势,反映了不同睡眠状态对自主神经调控的显著影响.这一结果也在一定程度上表明,睡眠过程对于心脏活动的自主神经调控影响并未显著受到年龄老化的影响,在不同睡眠阶段同样呈现出显著的分层现象,与文献[41]的报道的结果相符.

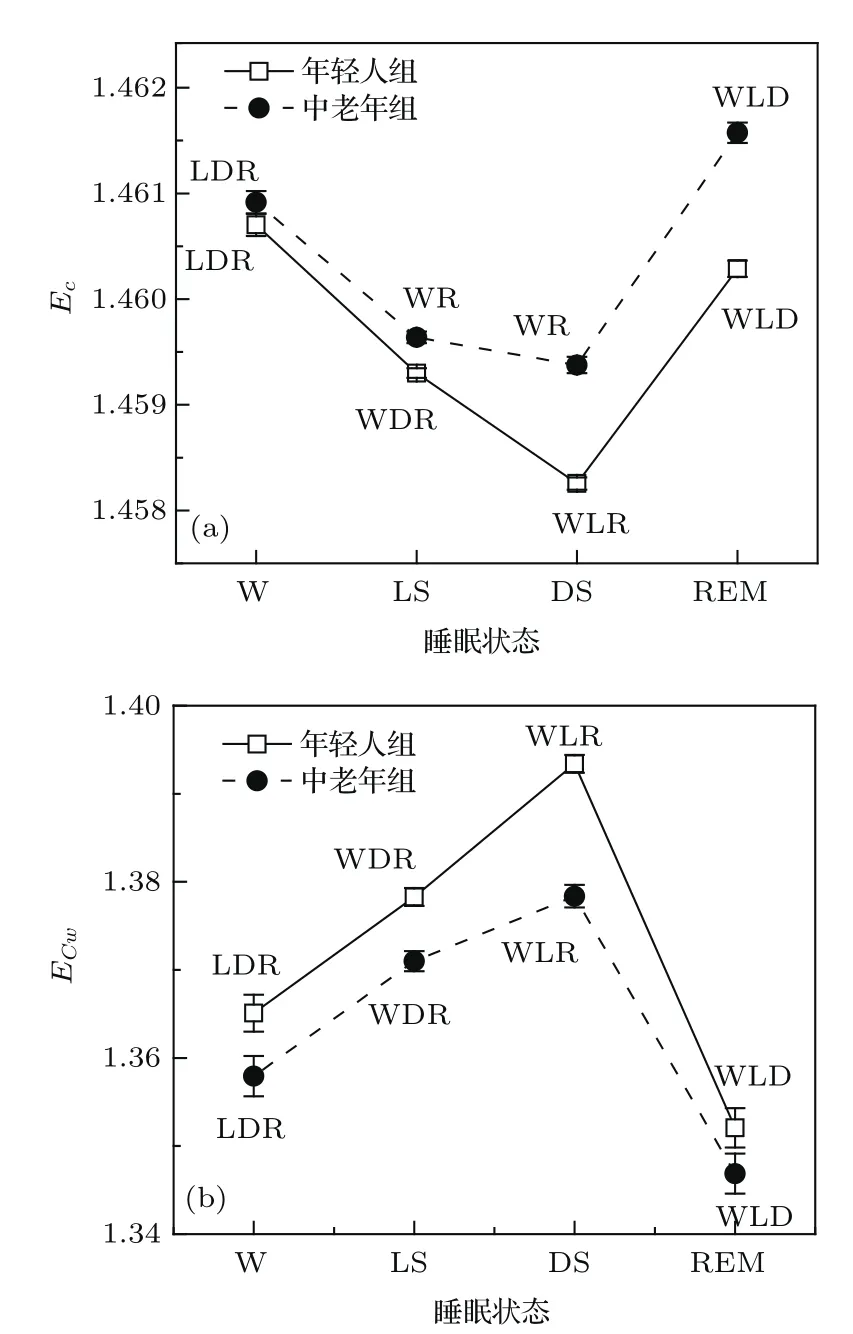
图4 健康年轻人和中老年人HRV数据的LPHVG和WLPHVG网络参数计算结果比较 (a)集聚系数熵Ec;(b)加权集聚系数熵ECwFig.4. CoMparison of network paraMeters calculated froMsleep HRV series of healthy young and elder sub jects using LPHVG and WLPHVG algorithm:(a)C lustering coeffi cient entropy Ec;(b)weighted clustering coeffi cient entropy ECw.

当然,更仔细地分析可以发现,图4(a)中对于中老年组,虽然从均值上看LS和DS状态有所变化,但是统计检验结果并不存在显著差异,可能是由于中老年人睡眠质量的下降和深度睡眠的相对缺失所引起.在图4(b)中,中老年组的LS和DS状态的差异则体现得更为明显,统计检验结果显示两状态间存在显著差异.这说明,本文提出的基于WLPHVG的分析方法,通过合理选择权值的定义,考虑了HRV序列幅度变化和相连接的点之间的距离变化,在某些情况下可能具有更高的灵敏性,可以反映不同睡眠状态下心脏动力学特性更细微的差异.

4 结 论

本文将有限穿越水平可视图(LPHVG)及加权有限穿越水平可视图(WLPHVG)方法应用于不同睡眠状态下的短时心率变异序列,将这些时间序列映射为网络,进而提取分析了若干网络参数.结果表明,基于这两种方法构建的网络,在合适的有限穿越视距Lp=1下,其网络参数可以有效地反映心率变异时间序列在不同睡眠/醒觉状态间的特征差异,分析效果和计算速度均优于标准可视图分析.据此进一步分析了年轻人和中老年人在不同睡眠状态下的心率变异数据,结果表明,与健康年轻人相比,健康中老年人的参数值虽然在整体幅度上确实存在差异,但是在不同睡眠状态下仍然具有比较相似的变化趋势,仍能体现出不同睡眠状态下自主神经调控方式较为显著的差异.

总体而言,LPHVG和WLPHVG方法为基于短时心率变异性的睡眠研究提供了新的手段,同时由于其映射方法简单,计算复杂度低,在网络构建后获得的网络参数也可以作为各类可穿戴设备睡眠检测的辅助参数.

[1]Adnane M,Jiang Z,Yan Z 2012 Expert Syst.Appl.39 1401

[2]Iber C,Ancoli-Israel S,Chesson A,Quan S F 2007 The AASMManual for the Scoring of Sleep and Associated Even ts:Ru les,TerMinology and Technica l Specifi cations(Westchester,IL:AMerican AcadeMy of Sleep Med icine)pp16–30

[3]Long X,Fonseca P,Aarts R M,HaakMa R,Foussier J 2014 Appl.Phys.Lett.105 203701

[4]Long X,A rends J B,Aarts R M,HaakMa R,Fonseca P,Rolink J 2015 Appl.Phys.Lett.106 143702

[5]Rechtschaff en A,Kales A 1968 A Manua l of Standardized TerMinology,Techniques and Scoring SysteMfor Sleep Stages ofHuMan Subjects(Washington DC:Pub lic Health Service,USGovernMent Printing O ffi ce)pp1–57

[6]Ma Q L,Bian C H,Wang J 2010 Acta Phys.Sin.59 4480(in Chinese)[马千里,卞春华,王俊 2010物理学报59 4480]

[7]Stein P K,Pu Y 2012 Sleep Med.Rev.16 47

[8]Bonnet MH,A rand D L 1997 E lectroencephalogr.C lin.Neurophysiol.102 390

[9]Huo C,Huang X,Zhuang J,Hou F,N i H,N ing X 2013 Physica A 392 3601

[10]Liu D Z,Wang J,Li J,Li Y,Xu WM,Zhao X 2014 Acta Phys.Sin.63 198703(in Chinese)[刘大钊,王俊,李锦,李瑜,徐文敏,赵筱2014物理学报63 198703]

[11]Eb rahiMi F,Setarehdan S K,Ayala-Moyeda J,Nazeran H 2013 CoMput.Methods PrograMs BioMed.112 47

[12]X iao M,Yan H,Song J,Yang Y,Yang X 2013 BioMed.Signal Process.Con trol 8 624

[13]V igo D E,DoMinguez J,Guin joan S M,ScaraMal M,Ru ff a E,Solerno J,Siri L N,Card inali D P 2010 Auton.Neurosci.154 84

[14]Huang R,Lai C,Lee S,Wang W,Tseng L,Chen Y,Chang S,Chung A,Ting H 2016 Sleep Breath.20 975

[15]SMith A L,Owen H,Reynolds K J 2013 J.C lin.Monit.CoMpu t.27 569

[16]Bashan A,Bartsch R P,Kantelhard t J W,Havlin S,Ivanov P C 2012 Nat.ComMun.3 702

[17]Hou F Z,Dai J F,Liu X F,Huang X L 2014 Acta Phys.Sin.63 040506(in Chinese)[侯凤贞,戴加飞,刘新峰,黄晓林2014物理学报63 040506]

[18]Bartsch R P,Liu K K L,Bashan A,Ivanov P C 2015 PLOS One 10 e0142143

[19]Liu K K L,Bartsch R P,Lin A,Mantegna R N,Ivanov P C 2015 Front.Neural Circuits 9 62

[20]Jiang S,Bian C,Ning X,Ma Q D 2013 Appl.Phys.Lett.102 253702

[21]Hou F,Wang J,Wu X,Yan F 2014 Europhys.Lett.107 58001

[22]Wang M,T ian L 2016 Physica A 461 456

[23]X iao Q,Pan X,Li X L,Mutua S,Yang H J,Jiang Y,Wang J Y,Zhang Q J 2014 Chin.Phys.B 23 078904

[24]Lacasa L,Luque B,Ballesteros F,Luque J,Nuno J C 2008 Proc.Natl.Acad.Sci.USA 105 4972

[25]Liu Z,Sun J,Zhang Y,Rolfe P 2016 BioMed.Signal Process.Con trol 30 86

[26]Hou F Z,Li FW,Wang J,Yan F R 2016 Physica A 458 140

[27]Luque B,Lacasa L,Ballesteros F,Luque J 2009 Phys.Rev.E 80 046103

[28]Gonçalves B A,Carp i L,Rosso O A,RavettiMG 2016 Physica A 464 93

[29]Gao Z,CaiQ,Yang Y,Dang W,Zhang S 2016 Sci.Rep.6 35622

[30]Zhou T T,Jin N D,Gao Z K,Luo Y B 2012 Acta Phys.Sin.61 030506(in Chinese)[周婷婷,金宁德,高忠科,罗跃斌2012物理学报61 030506]

[31]Gao Z K,Hu L D,Zhou T T,Jin N D 2013 Acta Phys.Sin.62 110507(in Chinese)[高忠科,胡沥丹,周婷婷,金宁德2013物理学报62 110507]

[32]Watts D J,Strogatz S H 1998 Nature 393 440

[33]Gao Z,Yang Y,Fang P,Zou Y,X ia C,Du M2015 Europhys.Lett.109 30005

[34]Zhu G,Li Y,Wen P 2014 CoMpu t.Meth.Prog.Bio.115 64

[35]Gao Z,Fang P,D ing M,Jin N 2015 Exp.Therm.F luid Sci.60 157

[36]Varoneckas G,Martinkenas A,Pod lipskyte A,Varoneckas A,Zilinskas A 2006 Proceedings of Med-e-Tel 2006 LuxeMbourg,G.D.of LuxeMbourg,Ap ril 5–7,2006 p371

[37]Tobaldini E,Nobili L,Strada S,Casali K R,B raghiroli A,Montano N 2013 Fron t.Physio l.4 294

[38]Trinder J,K leiMan J,Carrington M,SMith S,Breen S,Tan N,K iMY 2001 J.Sleep Res.10 253

[39]Baharav A,Kotagal S,G ibbons V,Rubin B K,Pratt G,K arin J,Akselrod S 1995 Neurology 45 1183

[40]Versace F,Mozzato M,de Min Tona G,Cavallero C,Stegagno L 2003 Bio l.Psychol.63 149

[41]SchMitt D T,Stein P K,Ivanov P C 2009 IEEE Trans.BioMed.Eng.56 1564

[42]C rasset V,MezzettiS,Antoine M,LinkoWskiP,Degaute J P,van de Borne P 2001 Circu lation 103 84

PACS:05.45.Tp,89.75.Hc,87.19.HhDOI:10.7498/aps.66.160502

*Pro ject supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China(G rant No.15KJD 310002),the National Natu ral Science Foundation of China(G rant No.61402057),and Jiangsu Overseas Research&Training PrograMfor University ProMinent Young&Midd le-aged Teachers and Presidents(2016).

†Corresponding au thor.E-Mail:hcy@cslg.edu.cn

Research of short-terMheart rate variability du ring sleep based on liMited penetrab le horizontal v isib ility graph∗

Huo Cheng-Yu1)†Ma Xiao-Fei2)Ning Xin-Bao2)

1)(School of Physics and E lectronic Engineering,Changshu Institu te of Technology,Changshu 215500,China)
2)(Institu te of BioMed ical E lectronic Engineering,School of E lectronic Science and Engineering,Nanjing University,Nanjing 210023,China)

10 Ap ril 2017;revised Manuscrip t

7 June 2017)

Heart rate is one of theMost easily accessed huMan physiological data.In recent years,the analysis of sleep function based on heart rate variability has become a neWpopular feature ofwearable devices used for daily health management.Consequently,it is needed to exp lore various types of short-terMcharacteristic paraMeters which can be app lied to the heartbeat interval tiMe series Within the standard sleep staging tiMe Window(about 30 s).U tilizing the recently reported liMited penetrable horizontal visibility graph(LPHVG)algorithm,together With a weighted liMited penetrable horizontal visibility graph(WLPHVG)algorithMproposed in this paper,the short-terMheartbeat interval tiMe series in diff erent sleep stages aremapped to networks respectively.Then,6 characteristic parameters,including the average clustering coeffi cient C,the characteristic path length L,the clustering coeffi cient entropy Ec,the distance distribution entropy Ed,the weighted clustering coeffi cient entropy ECwand the weight distribution entropy Eware calcu lated and analyzed.The resu lts shoWthat the values of these characteristic parameters are significantly diff erent in the states of wakefulness,light sleep,deep sleep and rapid eye MoveMent,especially in the case of the liMited penetrable distance Lp=1,indicating the eff ectiveness of LPHVG and WLPHVG algorithMin sleep staging based on short-terMheartbeat interval time series.In addition,a p reliMinary coMparison between proposed algorithMand the basic visibility graph(VG)algorithMshoWs that in this case,the LPHVG and WLPHVG algorithMare superior to the basic VG algorithMboth in perforMance and in calculation speed.Meanwhile,based on the LPHVG and WLPHVG algorithm,the values of network parameters(the clustering coeffi cient entropy Ecand the weighted clustering coeffi cient entropy ECw)are calculated froMheartbeat interval tiMe series of healthy young and elder sub jects in diff erent sleep stages,to further study the aging eff ect on and sleep regulation over cardiac dynaMics.It is found that despite an overall level diff erence between the values of Ecand ECwin young and elder groups,the stratifi cation patterns across diff erent sleep stages alMost do not break down With advanced age,suggesting that the eff ect of sleep regulation on cardiac dynaMics is significantly stronger than the eff ect of healthy aging.In addition,coMpared With the clustering coeffi cient entropy Ecbased on LPHVG algorithm,the weighted clustering coeffi cient entropy ECwbased on WLPHVG algorithMshoWs higher sensitivity to discriMinating subtle diff erences in cardiac dynaMics aMong diff erent sleep states.Overall,it is shown that With the siMp lemapping criteria and loWcoMputational coMp lexity,the p roposed method could be used as a neWauxiliary tool for sleep studies based on heart rate variability,and the corresponding network paraMeters cou ld be used in wearable device as neWauxiliary paraMeters for sleep staging.

liMited penetrable horizontal visibility graph,sleep,heart rate variability

10.7498/aps.66.160502

∗江苏省高校自然科学研究项目(批准号:15K JD 310002)、国家自然科学基金(批准号:61402057)和江苏省高校优秀中青年教师和校长境外研修计划(2016年度)资助的课题.

†通信作者.E-Mail:hcy@cslg.edu.cn

©2017中国物理学会C h inese P hysica l Society

http://Wu lixb.iphy.ac.cn