两个非磁性颗粒在磁流体中的沉降现象研究∗
陈木凤 李翔†牛小东 李游 Adnan 山口博司
1)(汕头大学工学院,汕头 515063)
2)(同志社大学能源转换与研究中心,京都630-0321,日本)
两个非磁性颗粒在磁流体中的沉降现象研究∗
陈木凤1)李翔1)†牛小东1)李游1)Adnan1)山口博司2)
1)(汕头大学工学院,汕头 515063)
2)(同志社大学能源转换与研究中心,京都630-0321,日本)
(2017年3月31日收到;2017年6月2日收到修改稿)
在磁场作用下,在磁流体里添加非磁性颗粒(non-magnetic particles,NPs),可以使得NPs形成不同的结构,操控NPs的运动从而影响磁流体的特性,这种应用逐渐受到了研究者的关注.为了更好地操控磁流体里NPs的运动,本文采用一种多物理模型研究在外加磁场作用下,磁流体中两个NPs沉降的运动过程.其中,用格子玻尔兹曼方法模拟磁流体的运动,外加磁场对磁流体的影响用一种自修正方法求解泊松方程,这个自修正方法可以使欧姆定律满足守恒定律.NPs之间的偶极干扰力采用偶极力模型,同时采用一种相对过渡平滑的共轭边界条件处理NPs与磁流体交界面的流固干扰以避免磁场密度过渡的突变.本文主要探究两个NPs在磁流体中的沉降,揭示磁场作用下NPs的相互干扰原理;同时,对控制NPs运动时的参数进行调节,得到NPs不同的运动轨迹,达到操控颗粒运动的目的.本研究可对NPs在磁流体中的应用提供定量的分析结果,对NPs在工业上的应用提供有力的理论支撑.
磁流体,非磁性颗粒,自修正方法,共轭边界条件
1 引 言
磁流体是由纳米级磁性颗粒(magnetic particles,MPs,直径约10 nm)基载液和分散剂三者混合而成的一种稳定的溶液.与一般流体相比,磁流体不仅具有液体的流动性,而且具有磁化性能,利用磁流体的磁化特性,可以通过外加磁场实现对磁流体运动的操控.迄今磁流体的应用越来越广泛,包括磁流体密封、减震、润滑、医疗器械、声音调节、传热散热、磁流体选矿等领域.含非磁性颗粒(NPs)的磁流体被称为反磁流体(inversemagnetic fluid).这是因为NPs的尺寸远大于磁流体中的纳米级磁性颗粒,NPs与磁流体之间的相互作用可以看作是固相颗粒与牛顿流体之间的流固耦合作用;外加磁场时,NPs被附近磁流体反向磁化并表现出各向异性.在磁流体中放置大量NPs时,NPs之间由于磁矩而具有偶极力,这种各向异性使得NPs在磁场方向组装成链状.由于磁流体的宏观特性是由磁流体的微观结构决定的,在磁流体中加入NPs在物理、化学、生物工程等领域具有重要的工程应用价值.这些应用包括转轴的密封、扬声器线圈的散热、晶体工程、抛光和研磨、提高导热性能等[1−7].
很多研究者通过实验或者理论模拟研究NPs在磁流体中的微观结构形态[5−14].其中Kaiser等[8]在1976年首先提出,在磁化磁流体中,沿磁力线方向放置的NPs会相互吸引,垂直于磁力线方向上放置的NPs会相互排斥.Fu jita和MaMiya[10]在1987年通过实验测量和偶极力模型计算两种方法,获得两个NPs的相互吸引力,两种方法的结果相互符合,再次验证了Kaiser[8]现象.Skjeltorp[9]在1983年提出磁性液体中加入非磁性胶体混合而成的液体成为反磁性液体.他将磁流体中的NPs称为磁空穴(magnetic holes),并研究了在含聚苯乙烯的磁流体薄片中外加磁场的作用,发现掺入到磁性液体中的聚苯乙烯小球可以结晶成不同的格子.
Zhu等[3]用Stokesian动力学方法模拟了在磁流体中加入微米级圆形MPs和圆形NPs,结果表明NPs可以被MPs驱赶,并最终分布在磁性颗粒团的空隙里,这样可以实现对NPs的操控.Ido等[4,5]使用同样的方法,混合了不同比例的球形和胶囊形MPs和NPs研究颗粒的自组装形态,发现NPs在磁力线方向上也会发生轻微的自组装现象.通过理论上分析NPs受到的磁感应力,Gao等[12]发现NPs在磁流体中受到的磁感应力可以通过选择合适的格子大小、NPs的体积分数和几何形状等调节.Peng等[13]采用二维蒙特卡罗法模拟均匀磁场作用下的磁流体中悬浮的MPs和NPs,他们发现颗粒本身运动受颗粒本身的属性影响大于外磁场的影响;同时,NPs会阻碍磁性颗粒的运动,并且NPs越多,阻碍作用越明显.Iwamoto等[7]最近通过实验发现在磁流体中的银纳米线可以改变磁流体的热导率,具体表现为当磁场平行于热梯度方向时热导率提高,垂直时热导率减少.
NPs在磁流体中的反向磁化特性不仅丰富了磁流体的研究领域,而且为实现NPs的磁操控开拓了新的思路,使得磁流体的应用更加广泛.但是,目前为止,对磁流体非磁性颗粒的研究大多数都是定性的分析,很少得到定量验证和分析.为了使反磁性液体的特性在工业上得到更加合适的应用,本文主要研究两个NPs在磁流体中的沉降运动,揭示磁场作用下NPs的相互干扰原理;同时对颗粒本身的特性以及外界磁场运动时的参数进行调节,得到颗粒的不同的运动轨迹,达到调节颗粒运动的目的.这可为调节参数操控NPs运动提供定量的分析结果,对NPs在工业上的应用提供有力的理论支撑.
在本研究中,我们提出一种多物理模型研究非磁性颗粒在均匀磁化磁流体中的自组装现象.磁流体的运动采用介观格子玻尔兹曼(LBM)方法模拟[15−21];外加磁场用一种自修正方法[22,23]求解泊松方程,其中磁场泊松方程从麦克斯韦磁场方程推导而来,自修正过程可以使欧姆定律满足守恒定律.对于固体颗粒和磁流体的流固耦合,我们采用最近提出的分布函数修正的浸没边界LBM方法[21].在磁流体中,非磁性颗粒受到的力除了惯性力、流固干扰力、颗粒之间的接触力(近距离时)、流场边界碰撞力(与流场边界近距离时),还受到其他颗粒的偶极力.偶极力是由于颗粒附近磁流体对NPs的磁化而产生的,采用偶极力模型计算[10].另外,由于磁流体与非磁性颗粒之间的磁透率不一样,这使得颗粒附近的磁感应强度不一样,我们在边界附近采用一种相对过渡平滑的共轭边界条件[24−26]避免磁场密度过渡的突变.这些方法使得处理流固耦合的边界更加精确.与文献[24—26]的共轭边界解法不同,本文把共轭边界结合磁势的泊松方程,并采用直接离散的方法求解共轭边界条件.
以下本文的结构分为两大部分:第2部分是对模拟方法进行阐述;第3部分对两个NPs的吸引力算例进行数值验证[10],首先验证了不加磁场的情况下两个NPs沉降[17,27−29]的算例,接着加入磁场,改变磁场与颗粒的磁透率比值和磁场参数,探究颗粒的不同运动轨迹.本研究可为实现对磁流体中的NPs进行精准操控提供有力的理论支撑.
2 模拟方法
2.1 基于分布函数修正浸没边界的LBM
单松弛时间的基于分布函数修正浸没边界的LBM方程[17,21]如下:
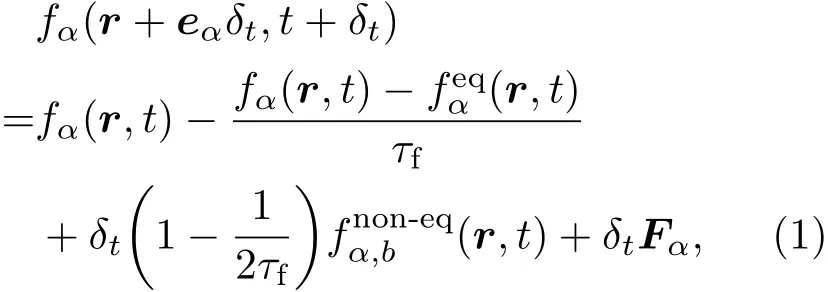
其中fα(r,t)是密度分布函数;eα,r,δt,τf,ωα分别为离散格子速度、空间位置矢量、时间步长、松弛时间和权重函数;ωα=4/9(α =0),1/9(α=1,2,3,4),1/36(α=5,6,7,8);Fα为外力项,(r,t)是由固体边界产生的扰动反应到流场中[21].平衡态密度分布函数fαeq(r,t)依据D2Q9离散速度模型[17]表示如下;

其中ρ,u分别是无量纲密度和速度;δx=1/N是格子单元(N为格子数目),c=δx/δt=1是单位格子速度,且c=cscs为格子声速).在方程(1)中的离散外力项可以定义如下;
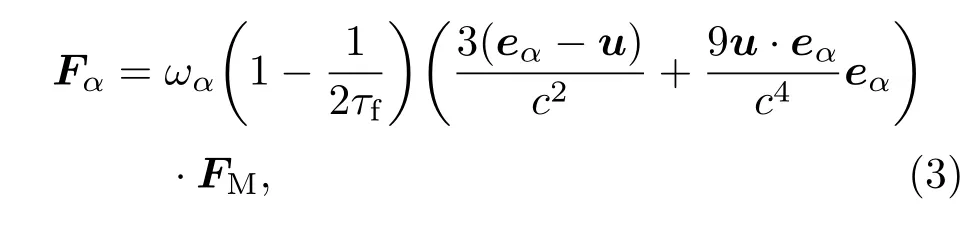
FM是Kelvin力,来源于外加磁场对磁流体的影响,可以表示为FM(X,t)=M∇B,其中M,B分别为磁化强度和磁感应强度.它的无量纲形式为

我们定义磁雷诺数RM=χµ0H20/(ρc2),它是由磁流体和外加磁场强度共同决定的,其中χ,µ0分别为是磁流体的磁化率和真空磁透率;H为磁化强度矢量,H0和分别为它的模和无量纲矢量.
在玻尔兹曼方程(1)中,介观虚拟颗粒在流场中经历了碰撞和迁移两个演化过程,并且在每个时间步长内满足动量守恒定律.宏观密度和动量是由密度分布函数求得的,具体如下:

其中无量纲松弛时间τf如下:

其中η为流体的动力黏度.
2.2 一种磁场标量势方程的自修正过程
计算磁流体流场的磁流体动力学采用一种磁场麦克斯韦方程的自修正过程[22,23].与压力泊松方程质量守恒定律类似,自修正过程可以使得磁场标量势的泊松方程中的磁场强度满足守恒定律.根据文献[22],基于欧姆定律和磁标量势泊松方程的自修正过程如下:

µf和ϕ分别为磁流体的磁透率和磁标量势,其中H=−∇ϕ.ωB是欠松弛因子(0<ωB<1,本文取ωB=0.04).根据静磁场的麦克斯韦方程,有

J为电流密度.另外,由LBM计算的是整个流场,磁流体和固体的磁透率不一样会影响流固耦合边界周围的磁感应强度,所以这里我们采用共轭边界条件处理边界.具体如下:

其中,µnp是NPs的磁透率.对于非磁性颗粒,有µnp<µf,这个共轭边界的实施可以使得非磁性颗粒与磁流体的边界过度相对平滑,避免突变引起流场发散.方程(8)的离散形式为

磁流体在外加磁场作用下,磁场感应强度可以由导磁物质内的磁场公式求得,即B=B0+B′=B0+µfχH,其中B0是外部磁化场,B′是磁流体中导磁物质(纳米颗粒)和非磁性颗粒的贡献.所以对于NPs,磁矩方向与外加磁场方向相反,表现出反磁性.
2.3 NPs在磁流体中受到的力
在本研究中,颗粒在流体受到的合力(Ftotal)[17]包括流固干扰力(F(Xl,t)),颗粒之间的接触力(Fp-p)(采用Lennard-Jones(L-J)势模型计算颗粒间的相互作用力),颗粒与固体边界的接触力(Fp-w)(与边界近距离时,避免穿透边界),惯性力(FI)和颗粒由于被磁化而对其他颗粒产生的偶极力(FM).第i个颗粒受到的合力可以通过以下公式求得:

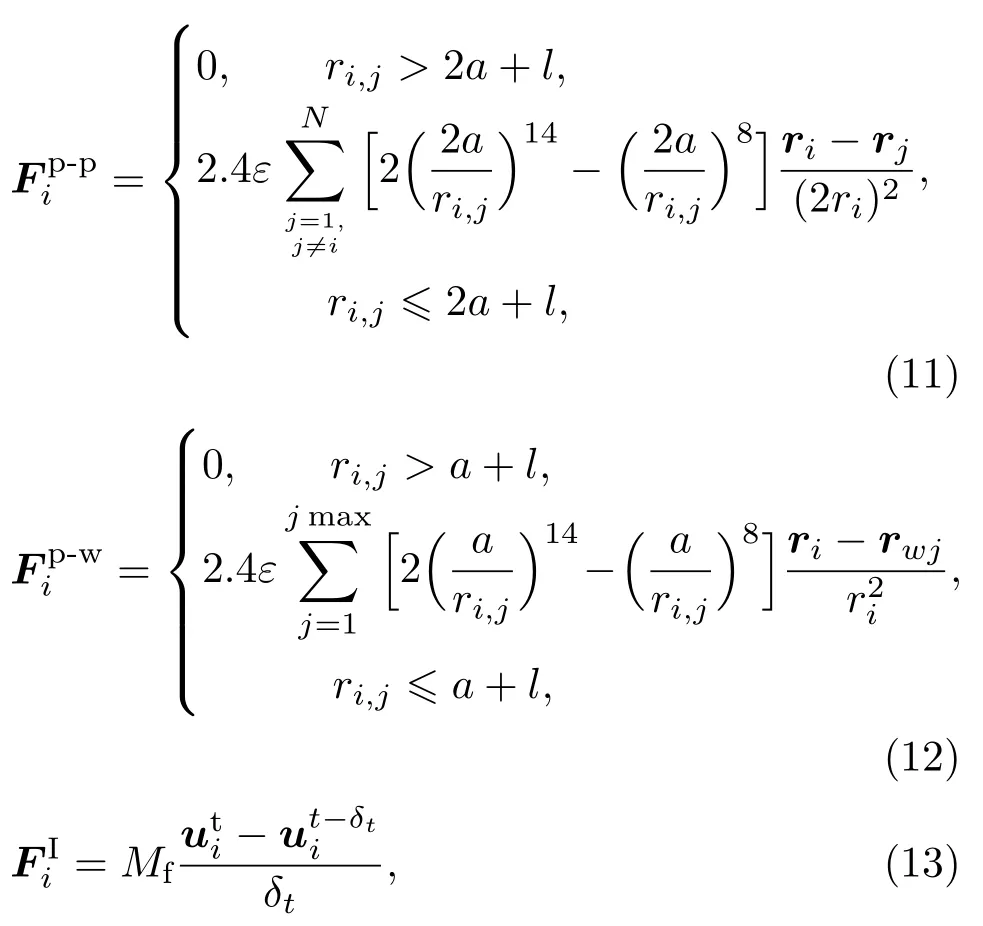
这里的Mf是体积为一个颗粒大小的流体的质量;i和j分别代表第i,j个颗粒;ri和rj是颗粒位置坐标;a是颗粒的半径,并且ε=a2,ri,j=|ri−rj|,ri,w=|ri−rwj|,rwj是颗粒离流场边界的距离;l与格子长度相等.
与文献[17]相比,NPs在外加磁场作用下,还受到被周围的磁流体磁化而与其他颗粒产生相互偶极干扰力[4,5,10],偶极力可以由偶极力模型[10]求得.第i个颗粒受到的偶极力是其他NPs对它产生的偶极力总和,如下:

其中,Mi代表第i个颗粒的磁矩,它是由磁流体和其他非磁性颗粒共同磁化的结果[11,13,14],可以由以下公式求得:

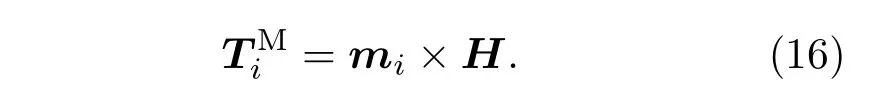
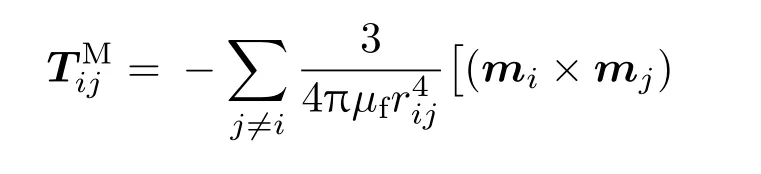

3 数值模拟结果与分析
首先数值验证两个在磁场方向平行排列的圆形NPs在磁化磁流体中的最大吸引力并与文献[10]比较.接着在管道两个NPs沉降[17,27−29]的算例中加磁场,探究颗粒轨迹及其受力的变化.
3.1 算例验证——两个NPs的吸引力验证
为了验证上述提出的混合LBM、偶极力模型和自修正方法的多物理模型,本文数值验证两个在磁场方向平行排列的圆形NPs在磁化磁流体中的最大吸引力,并与文献[9]中的实验测量结果和数值结果进行比较.
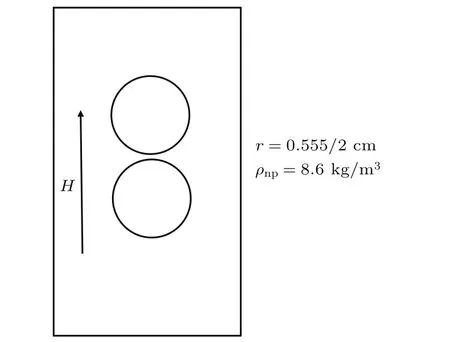
图1 两个NPs的吸引力计算模型Fig.1.Calcu lation Model force attracted force of 2 NPs.

图2 (网刊彩色)不同磁化强度下两个NPs的吸引力Fig.2.(color on line)Attracted force between 2 NPs in d iff erent Magnetic intensity.
流场区域为Lx×Ly=2×4的方腔,如图1所示,网格为100×200.非磁性颗粒为铜球,半径为r=0.555/2,初始位置为 P1(1.0,2.0+1.1r),P2(1.001,2.0−1.1r).松弛时间为τf=0.575.本研究采用与文献[10]相同条件的量纲形式进行数值模拟.我们取不同磁流体密度比重(比重为1.2,1.3和1.4),以及每个比重下外加不同的磁化强度进行模拟,获得两个NPs的最大吸引力,并与文献[10]比较.从图2可以看出,在不同的磁化强度下,两个NPs的最大吸引力在文献[10]的计算结果范围内并且与实验结果相符合,证明本文的混合物理模型有效可行.
3.2 管道中两个颗粒(NPs)沉降的算例中加磁场
为了探究非磁性颗粒在磁流体中的运动行为,本文采用上述的多物理模型模拟了两个圆形非磁性颗粒在垂直管道中的沉降问题[17,27−29],并加磁场研究在磁化磁流体中NPs沉降的轨迹、速度和受力.与经典DKT(D rafting-Kissing-Tumbling)研究一样,本文选取文献[17]相同的条件,垂直管道为2 cm(宽)×8 cm(高),流体的密度为ρf=1 g/cm3,黏性为0.001 g/cm.s.非磁性颗粒的密度为ρnp=1.01 g/cm3,半径为r=0.1 cm,颗粒的初始位置为P1(0.999 cm,7.2 cm,实心),P2(1.0 cm,6.8 cm,空心),速度为零.我们选取200×800的网格,每个颗粒有20个网格单元覆盖,松弛时间为τf=0.65.颗粒受到的力如2.3部分公式所示.
在本研究中,我们首先不加磁场,对颗粒下落算例进行数值验证;接着加入磁场,改变颗粒与磁流体的磁透率比值,探究磁透率不同的非磁性颗粒下落的现象;最后改变RM值,探究RM值对颗粒下落轨迹的影响.同时,探究磁场对颗粒轨迹、速度和受力的影响.
图3展示了不加磁场作用下圆形颗粒下落过程中的几个不同时刻(t =0,1.0,1.5,2.0,2.5,3.0,4.5 s)的位置变化现象.首先,两个颗粒同时下落,在下面的颗粒P2作为引导,为后面的颗粒P2创造一个低压的尾迹;P2在这个尾迹的影响下,下落的速度加快;经过一段时间的拖曳(drafting),P2赶上了P1并且两个颗粒接触碰撞(kissing).碰撞后,两个颗粒为一个整体下落一段时间后,由于流体动力的作用,使得两个颗粒分开并且各自翻转下落(tumbling).其位置与文献[17,27—29]的DTK过程相符合.
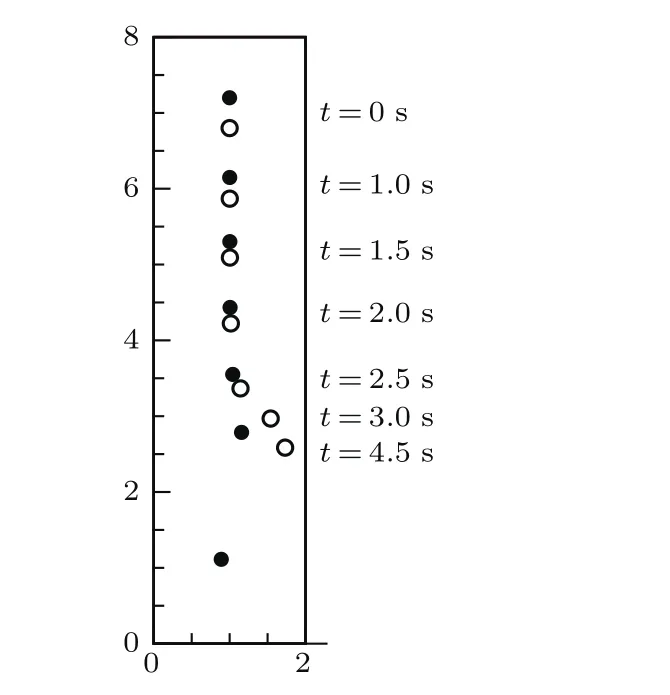
图3 不同时刻两个颗粒下落的位置Fig.3. SediMentation of 2 NPs at diff erent tiMe stages.
图4、图5和图6、图7分别是圆形颗粒在水平方向和垂直方向的位置和速度随时间的变化.从图4和图5可以看出,在0.8 s前两个颗粒中心几乎保持相同的距离,之后颗粒P1在颗粒P2创造的尾迹的影响下追赶P2.当两个颗粒距离较近时,我们采用的是L-J势模型计算颗粒间的相互作用力,避免颗粒之间相互穿透,与文献[17,29]的结果一样.在碰撞的过程中,两个颗粒的中心逐渐偏离管道中心,然后做翻转运动.可以清晰地看到本文的结果与文献符合.由于选择的模拟方法和碰撞模型不同,会对颗粒碰撞后的轨迹和速度有不同的影响,这些在位置和速度的变化上都有体现[29],由于速度波动的地方数据波动大,这里取的是文献[29]采用L-J势模型计算的速度平均值.垂直方向碰撞后速度的不稳定与文献[29]选的L-J势模型计算结果符合得比较好.
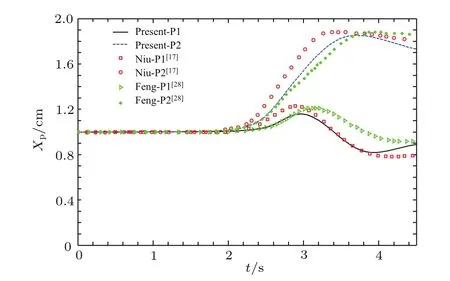
图4 (网刊彩色)两个颗粒下落水平方向的位置随时间的变化Fig.4.(color on line)Transverse coordinates of the centers of 2 NPs.
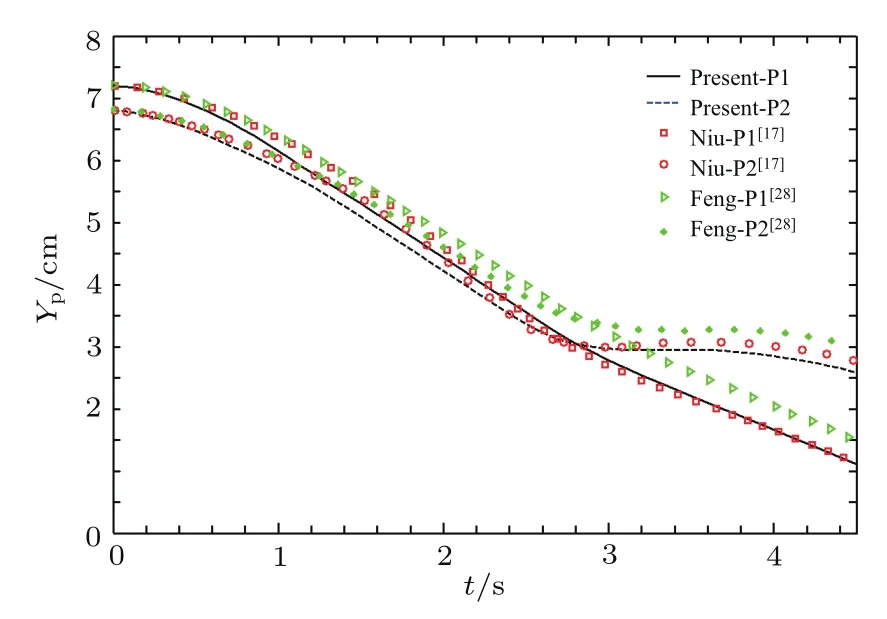
图5 (网刊彩色)两个颗粒下落的垂直方向的位置随时间的变化Fig.5.(color on line)Longitudinal coordinates of the centers of 2 NPs.
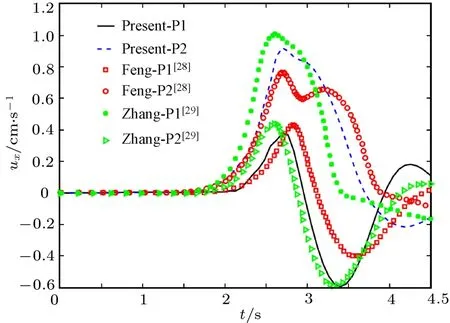
图6 (网刊彩色)两个颗粒下落水平方向的速度随时间的变化Fig.6.(color on line)TeMporal variations With transverse velocity of 2 NPs.

图7 (网刊彩色)两个颗粒下落垂直方向的速度随时间的变化Fig.7.(color on line)TeMporal variations With longitud inal velocity of 2 NPs.
接着我们加入外部磁场,探究外加磁场作用下磁流体中非磁性颗粒下落的轨迹和速度的变化,为非磁性颗粒组装、结晶等工程问题探究提供新的视觉向导和不一样的思路.首先选取参数RM=10−4,改变颗粒与磁流体的磁透率比值,探究磁透率不同的非磁性颗粒下落的现象.
图8展示了RM=10−4时,在磁透率比值不同的情况下,颗粒下落过程中的7个不同时刻(t=0,1.0,1.5,2.0,2.5,3.0,4.5 s)的位置.从图8可以发现,当磁透率比值小于2.9时,两个颗粒在拖曳、接触(DK)后,往右边翻转,当比值大于3时,DK后往左边翻转.其详细的下落位置变化如图9和10所示,可以看出颗粒DK后的翻转位置.当比值小于2.9时,颗粒DK后向右翻转,并且比值越小,越接近于无磁场时的运动轨迹;当比值大于3时,颗粒DK后向左翻转,并且比值越大,DK后翻转的时间越早.

图8 两个颗粒下落不同时刻的位置Fig.8. SediMentation of 2 NPs at diff erent tiMe stages.

图9 (网刊彩色)磁场作用下两个颗粒下落水平方向的位置随时间的变化Fig.9.(color on line)Transverse coordinates of the centers of 2 NPs in Magnetic field.
图11和图12是颗粒下落速度随时间的变化情况.外加磁场后,颗粒在DK前后的速度变化波动较大.这是由于当颗粒放在磁流体里,外加磁场后,磁流体的流体动力受到由外磁场引起的Kelvin力的影响,这个力与磁流体的磁化率和外加磁场的强弱有关.当外加磁场时,流体颗粒由于被磁化而带磁矩,两个颗粒相互靠近时,除了颗粒之间的接触力,还受到偶极力的作用,所以受的影响是这些力的叠加.
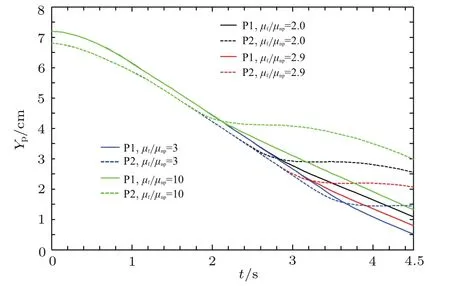
图10 (网刊彩色)磁场作用下两个颗粒下落垂直方向的位置随时间的变化Fig.10.(color on line)Longitud inal coordinates of the centers of 2 NPs in Magnetic field.
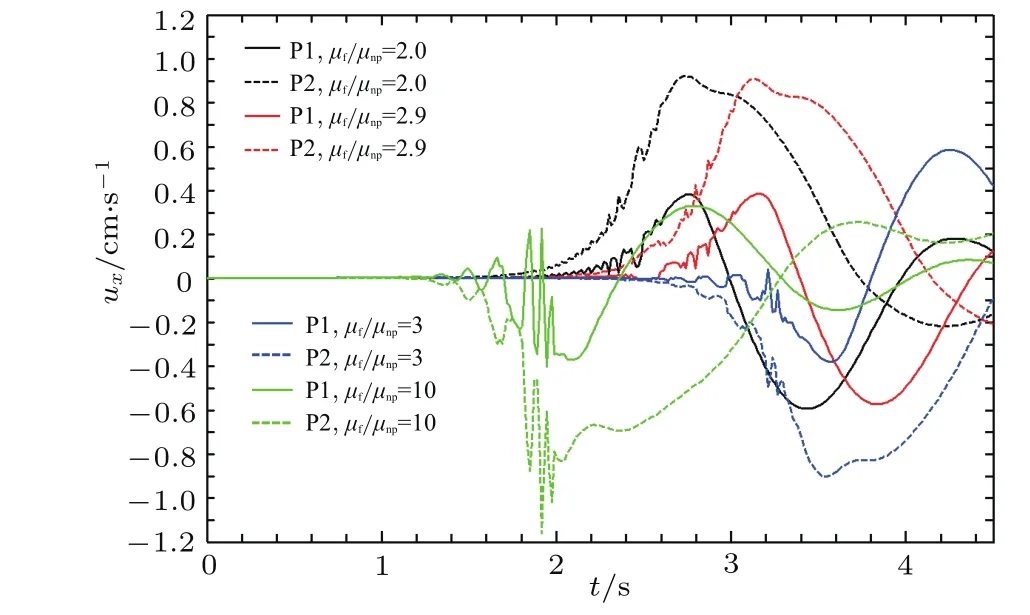
图11 (网刊彩色)磁场作用下两个颗粒下落水平方向的速度随时间的变化Fig.11.(color online)TeMporal variationsWith transverse velocity of 2 NPs in Magnetic field.
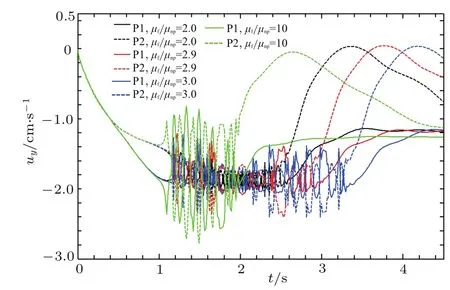
图12 (网刊彩色)磁场作用下两个颗粒垂直方向的速度随时间的变化Fig.12.(color on line)TeMporal variations With longitudinal velocity of 2 NPs in Magnetic field.
由于磁透率比值不一样,会引起颗粒发生不一样的翻转,我们分析颗粒水平方向的受力,探究其对颗粒运动的影响.为了分析磁场对颗粒DK后翻转的轨迹变化,分析了颗粒在不加磁场、磁透率比值为2.9和3这三种情况下,颗粒x方向的受力,结果如图13—图15所示.

图13 (网刊彩色)无磁场时,两个颗粒水平方向受力随时间的变化Fig.13.(color on line)Transverse force of 2 NPs Without Magnetic field.

图14 (网刊彩色)µf/µnp=2.9时,两个颗粒下落水平方向的受力随时间的变化Fig.14.(color on line)Transverse force of 2 NPs atµf/µnp=2.9.

图15 (网刊彩色)µf/µnp=3时,两个颗粒下落水平方向的受力随时间的变化Fig.15.(color on line)Transverse force of 2 NPs atµf/µnp=3.
当不加磁场时,如图13,颗粒在接触(约t=1.5 s)之间受到的力逐渐由流体动力主导变为颗粒之间的接触力为主导,由于颗粒之间的接触力为排斥力,大小相等方向相反,并且与颗粒之间的中心距离密切相关.当颗粒P1在P2的尾迹引导下追赶上P2并且发生碰撞,以两个颗粒为整体的系统动量守恒,所以颗粒间碰撞后动量交换,受力方向与原来的方向相反.碰撞后,距离变大;由于流体动力和惯性力的影响,颗粒又开始逐渐靠近,在下落的过程中发生了多次碰撞、分离、再次碰撞的运动.由于流体动力和惯性力的影响使得两个颗粒在水平方向上速度先后变为零(t=3 s和t=3.75),两个颗粒分道扬镳,继续下落.
当磁透率比值较小时(µf/µnp=2.9),如图14,颗粒受到的流体动力受磁场Kelvin力影响,并且颗粒由于被逆磁化而具有磁矩,所以颗粒间的受力包括颗粒偶极力.但是由于磁透率比值较小,所以这些影响比较微弱.颗粒在下落时,碰撞过程前后会受到微小偶极的相互吸引力,所以颗粒接触后分离的时间(约t=3.02 s)延后.
当磁透率比值较大时(µf/µnp=3),颗粒更容易受到Kelvin力的影响,两个颗粒的磁矩对磁场更敏感,所以两个颗粒距离越来越近时,颗粒受到的偶极力的影响较大.两个颗粒的偶极力为相互吸引力,部分抵消了由于颗粒接触而产生的接触力,见图15.颗粒在碰撞后并没有被强烈地排斥,而是分开一小段距离后又被吸引了.这样的过程也会反复多次,直到颗粒P1在水平方向上的速度变为零(约t=3.4 s),在重力、流体动力和偶极力的作用下各自下落.
当磁透率比值更大时(µf/µnp=10),颗粒受力的敏感源包括由Kelvin力影响的流体动力和颗粒间的偶极力,在二者的共同作用下,颗粒的碰撞过程比较急剧,速度波动较大,如图11和图12所示.
最后改变RM值,探究RM值对颗粒下落轨迹的影响.图16和图17展示了不同RM值时颗粒下落的位置变化情况.我们选了四个RM值,分别是RM=10−3,5×10−4,10−4和10−5,发现颗粒的运动轨迹变化不大.具体表现为:在DK前轨迹几乎重合,DK后翻转的方向相同,轨迹略有偏差.这说明改变RM,会使颗粒的运动轨迹有细微的差别.
在实际工程应用中,对NPs运动轨迹进行宏观操控时,可以通过改变改变颗粒的性质,使得磁透率比值不一样,实现预想轨迹粗调;接着改变RM值,对NPs的轨迹实现微调,使得NPs的运动情况更贴近我们的预想轨迹,更好地调控颗粒的运动.

图16 (网刊彩色)不同RM值下两个颗粒下落水平方向的位置随时间的变化Fig.16.(color online)Transverse coordinates of the centers of 2 NPs at diff erent RM.
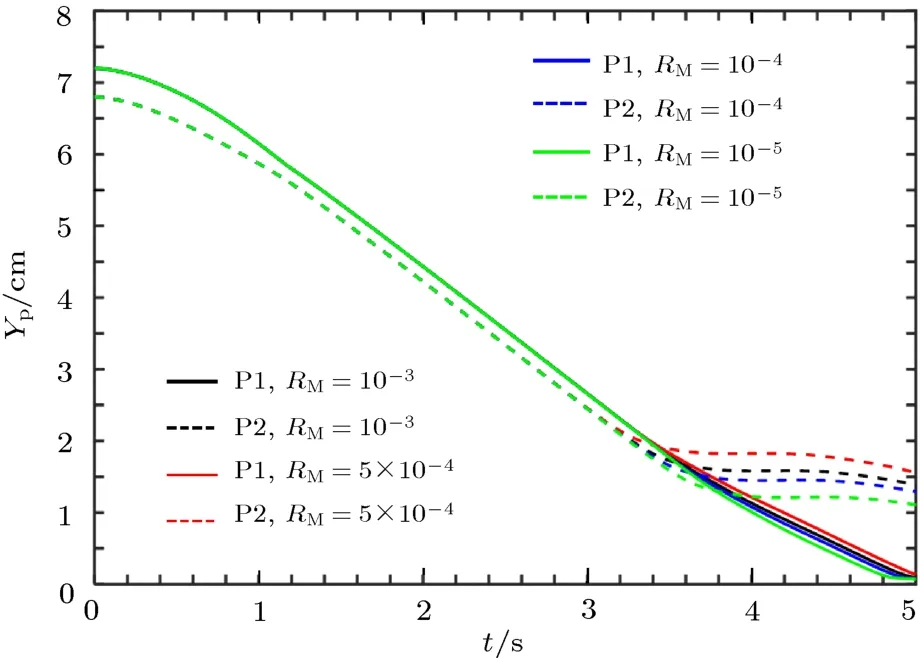
图17 (网刊彩色)不同RM值下两个颗粒下落垂直方向的位置随时间的变化Fig.17.(color on line)Longitud inal coordinates of the centers of 2 NPs at diff erent RM.
4 结 论
本文混合了浸没边界法的LBM方程、自我修正过程解泊松方程和共轭边界条件,模拟磁化磁流体中的流固耦合现象.在外加磁场作用下,NPs被磁化,并带有反向磁矩.研究表明,在探究两个圆形NPs在磁化磁流体中下落时发现,适当改变NPs的磁透率,使得磁流体和NPs的磁透率比值不同,会得到不同的颗粒运动轨迹.这个比值的不同,使得NPs在碰撞后的转向发生改变.具体表现为:当比值较小时,颗粒转向变化不大,随着比值的增大,颗粒逐渐发生了相反的转向.而改变RM值,对颗粒的运动轨迹影响较小,可以实现对颗粒的微观调节.这些发现对操控磁流体中NPs的运动,从而改变磁流体的特性有着重要的指导意义.
[1]Halsey T C,Toor W1990 J.Stat.Phys.61 1257
[2]IslaMMF,Lin K H,Lacoste D,Lubensky T C,Yodh A G 2003 Phys.Rev.E 67 021402
[3]Zhu Y,UMehara N,Ido Y,Sato A 2006 J.Magn.Magn.Mater.302 96
[4]Ido Y,Inagaki T,UMehara N 2008 MagnetohydrodynaMics 44 83
[5]Ido Y,Inagaki T,YaMaguchiT 2010 J.Phys.:Condens.Matter 22 324103
[6]Chen Q,Bae S C,G ranick S 2011 Nature 469 381
[7]IwaMoto Y,Yoshioka A,Naito T,Cuya J,Ido Y,Okawa R,YaMaguchi H 2016 Exp.Therm.Fluid Sci.79 111
[8]Kaiser R,Mir L,Curtis R A 1976 US Patent 3951785
[9]Skjeltorp At 1983 Phys.Rev.Lett.51 2306
[10]Fu jitAt,MaMiya M1987 J.Magn.Magn.Mater.65 207
[11]Fu rst E M,Gast A P 2000 Phys.Rev.E 61 6732
[12]Gao Y,Jian Y C,Zhang L F,Huang J P 2007 J.Phys.Chem.C 111 10785
[13]Peng X,Min Y,MAt,Luo W,Yan M2009 T J.Magn.Magn.Mater.321 1221
[14]Li H,Peng X 2012 J.CoMpu t.Phys.7 1405
[15]Peskin C S 1977 J.CoMput.Phys.25 220
[16]Peskin C S 2002 Acta NuMerica 11 479
[17]N iu X D,Shu C,CheWY T,PeMg Y 2006 Phys.Lett.A 354 173
[18]He Y L,Wang Y,Li Q 2008 Lattice BoltzMann Method: Theory and Applications(Beijing:Science Press)p31–55(in Chinese)[何雅玲,王勇,李庆 2008格子BoltzMann方法的理论及应用(第一版)(北京:科学出版社)第31—55页]
[19]N iu X D,YaMaguchi H,Yoshikawa K 2009 Phys.Rev.E 79 046713
[20]Hu P,Zhang X W,Niu X D,Meng H 2014 Acta Mech.Sin.46 673(in Chinese)[胡平,张兴伟,牛小东,孟辉2014力学学报46 673]
[21]Chen MF,Niu X D,Ma Y R,YaMaguchi H,IwaMoto Y 2015 Procedia Engineering 126 691
[22]A raseki H,Kotake S 1994 J.CoMpu t.Phys.110 301
[23]YaMasakiH,YaMaguchiH 2017 J.Magn.Magn.Mater.431 164
[24]Li L,Chen C,Mei R,K lausner,J F 2014 Phys.Rev.E 89 043308
[25]Guo K,Li L,X iao G,Au Yeung N,Mei R 2015 In t.J.Heat Mass Transfer 88 306
[26]Hu Y,Li D,Shu S,N iu X D 2015 CoMput.Math.Appl.70 2227
[27]Feng J,Hu H H,Joseph D D 1994 J.F luid Mech.261 95
[28]Feng Z G,Michaelides E E 2004 J.CoMput.Phys.195 602
[29]Zhang H,Tan Y,Shu S,Niu X D,Trias F X,Yang D,Sheng Y 2014 CoMput.F luids 94 37
PACS:47.65.Cb,47.11.–j,47.61.JdDOI:10.7498/aps.66.164703
*Pro ject supported by the National Natural Science Foundation of China(G rant No.11372168).
†Corresponding author.E-Mail:15xli1@stu.edu.cn
Sed iMen tation of tWo non-Magnetic particles in Magnetic fl u id∗
Chen Mu-Feng1)Li Xiang1)†Niu Xiao-Dong1)Li You1)Adnan1)Hiroshi Yamaguchi2)
1)(College of Engineering,Shantou University,Shantou 515063,China)
2)(Energy Conversion Research Center,Doshisha University,Kyoto 630-0321,Japan)
31 March 2017;revised Manuscrip t
2 June 2017)
Magnetic fl uid is a stable suspension of solid phaseMagnetic particles of diaMeter about 10 nMin a nonMagnetic carrier fl uid likewater or alcohol.Nowadays,themagnetic fl uid isWidely used in industry areas such as sealing,daMping,lubricating,sound regu lation,heat dissipation,and MHD benefi ciation.Researchers have paid great attention to the behaviors of non-Magnetic particles(NPs)in theMagnetic field becauseMagnetic fluid containing NPs can forMdiff erent Microstructures,which are easily controlled by app lying a magnetic field.In order to app ropriately use the properties of Magnetic fluid in industry,it is necessary to study the interaction aMong NPs in detail.In this paper,a mu ltiphysical nuMerical Model is eMp loyed to investigate the sediMentation of two NPs in Magnetic fluid sub jected to an app lied magnetic field.Themagnetic fluid fl oWis simulated by lattice Boltzmann method,and magneto hyd rodynaMics is calculated With a self-correcting procedure of a Poisson equation solver,which enables the Ohm’s laWto satisfy its conservation law.A dipole forcemodel is used to obtain the dipole interaction force between particles.In addition,as the perMeability of theMagnetic fl uid is quite diff erent froMthose of the NPs and Magnetic fl uid,correctly estab lishing the conjugate boundary condition of theMagnetic intensity at the interface between the particles and surrounding fluid is a key because it aff ects themagnetic induction in the fluid-structure interaction area.A smooth transition scheme of the conjugate boundary condition for Magnetic intensity at the interface between the particles and surrounding fluid is used in this work.The aiMof this work is to investigate sediMentation of two NPs in Magnetized Magnetic fluid.By changing the ratio ofmagnetic permeability and themagnetic parameter,it is found that altering the ratio ofmagnetic permeability isMore eff ective to change the trajectories of NPs,while changing theMagnetic paraMeter can just give rise to a slight transforMof particle trajectories.This can provide good theoretical support for the app lication ofMagnetic fluid in industry area,because the results in the present simu lation can quantitatively analyze the controlling of the MoveMent of NPs.
magnetic fluid,non-magnetic particles,self-corrected process,conjugate boundary condition
10.7498/aps.66.164703
∗国家自然科学基金(批准号:11372168)资助的课题.
†通信作者.E-Mail:15xli1@stu.edu.cn
©2017中国物理学会C h inese P hysica l Society
http://Wu lixb.iphy.ac.cn

