瑞利-泰勒不稳定问题的光滑粒子法模拟研究∗

杨秀峰 刘谋斌

1)(DepartMent of Mechanical Engineering,Iowa State University,AMes,IA 50011,USA)

2)(北京大学工学院,北京 100187)

瑞利-泰勒不稳定问题的光滑粒子法模拟研究∗

杨秀峰1)刘谋斌2)†

1)(DepartMent of Mechanical Engineering,Iowa State University,AMes,IA 50011,USA)

2)(北京大学工学院,北京 100187)

(2017年4月1日收到;2017年6月2日收到修改稿)

提出了一种适用于模拟多相流的光滑粒子法,该方法对密度方程在交界面处的离散格式进行了修正以适应多相流所涉及的大密度比问题,在不同相粒子之间施加了很小的排斥力以防止粒子穿透交界面,并采用了最新发展的双曲型光滑函数以消除应力不稳定问题.应用该多相流光滑粒子法模拟研究了单模态和多模态瑞利-泰勒不稳定问题.通过与文献中结果的对比研究表明:在模拟瑞利-泰勒不稳定问题时,本文方法的结果明显优于文献中的大部分光滑粒子法模拟结果,与Grenier等(2009 J.Comput.Phys.228 8380)的结果相当,但本文方法比Grenier等的方法简单方便.对于单模态瑞利-泰勒不稳定问题,研究了交界面的形态,涡结构的演化过程以及贯穿深度随时间的变化关系.对于多模态瑞利-泰勒不稳定问题,研究了交界面演化过程中小尺度结构合并成大尺度结构的过程,水平方向的平均密度随高度的变化关系,以及贯穿深度随时间的变化关系.

瑞利-泰勒不稳定性,光滑粒子法,多相流

1 引 言

瑞利-泰勒不稳定(Rayleigh-Taylor instability)问题是指当密度大的流体处于密度小的流体之上时,在重力的作用下产生的一种交界面不稳定现象.Rayleigh[1]最早从理论上分析了重力作用下密度不同的两种流体的稳定性,从理论上证明:当上层流体的密度小于下层流体的密度时,交界面是稳定的,扰动使交界面产生的振荡会逐渐衰减;相反,如果上层流体的密度大于下层流体的密度,则交界面是不稳定的,扰动导致的交界面振荡会被迅速放大.Taylor[2]从理论上分析了重力作用下上层流体密度大于下层流体密度时交界面的稳定性问题,指出交界面的初始扰动会随时间以指数关系增加,并给出了相应的变化公式.为了验证Taylor的理论结果,LeWis[3]做了一系列的实验,在圆柱形的装置中观测了不稳定交界面的演化过程.实验结果表明Taylor的结果适用于交界面演化的初始阶段.LeWis[3]的实验结果还表明交界面不稳定性的发展过程可分为三个阶段:首先是初始阶段,扰动幅度以指数增加;随后为过渡阶段,扰动幅度的增加速度逐渐增大到最大值;最后是匀速阶段,两种流体相互贯穿的速度不再增大,贯穿深度匀速增加.

瑞利-泰勒不稳定问题主要取决于两种流体的密度和重力加速度.重力加速度越大,不稳定性就越强.如果没有重力,则不会产生瑞利-泰勒不稳定现象.流体密度的影响一般用无量纲数——Atwood数(At)来表征:

其中ρH和ρL分别表示重的流体和轻的流体的密度.Atwood数的取值范围是0≤At≤1.当两种流体的密度相等时(At=0),不存在瑞利-泰勒不稳定问题.当两种流体密度差增大时,Atwood数也增大,交界面的不稳定性增强.当轻的流体不存在时(At=1),即上层流体置于真空之上,瑞利-泰勒不稳定问题就成了流体的自由下落问题.对于二维问题,当Atwood数较小时,相互贯穿的流体会形成两个反向旋转的涡.当Atwood数增大时,则涡的尺寸会减小.当Atwood数大到一定值时,上层密度大的流体穿过下层密度小的流体迅速下落,而密度小的流体则会迅速上浮[4].另外,流体的表面张力和黏性等因素也会影响瑞利-泰勒不稳定性,因为它们会对流体的相互贯穿起到一定程度的阻碍作用[5].

瑞利-泰勒不稳定问题不仅具有科学上的研究意义,而且具有应用上的研究价值[6−8].因此,在Rayleigh和Taylor之后,这一问题成了流体交界面稳定性研究的一个重要的基本问题.近几十年,研究者们发展了许多模型来预测瑞利-泰勒不稳定问题中两种流体相互贯穿的深度[9−13].然而,到目前为止,还没有一个模型能够与实验结果完全相符[10,14].对于交界面形状的演化过程,更是没有模型能够预测.随着计算流体力学的快速发展,数值模拟成了研究瑞利-泰勒不稳定问题的一个重要手段[15−19].

本文的目的是给出一种适用于模拟多相流的光滑粒子法(smoothed particle hydrodynaMics,SPH method),并应用该方法模拟研究单模态和多模态瑞利-泰勒不稳定流动的演化过程.

2 数值方法

光滑粒子法是一种无网格粒子类方法[20−24].在模拟流体问题时,光滑粒子法将连续的流体离散成可运动的粒子,粒子之间通过光滑函数进行关联,然后将流体的控制方程离散成相应的粒子方程进行数值求解.

在光滑粒子法中,任一函数f在粒子a上的值可以离散成如下求和形式:

其中脚标a和b表示粒子,r表示位置矢量,W表示光滑函数(也称为核函数),V表示粒子的体积.参数h表示光滑长度,用于控制光滑函数W的宽度,把上式中的求和范围限制在有限的区域内.本文使用的光滑函数为双曲型核函数[25,26]:

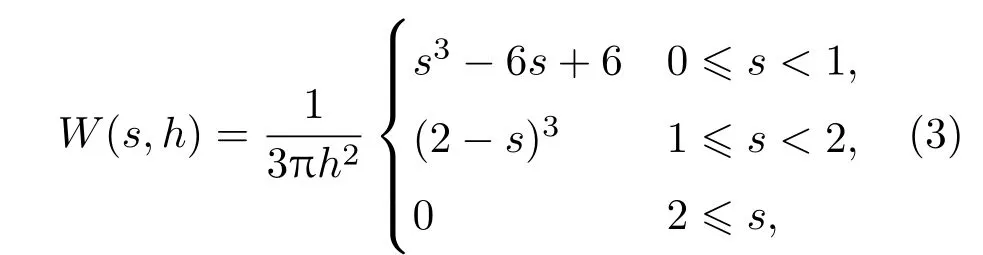
其中s=r/h,r表示两个粒子之间的距离.该光滑函数能够有效地消除光滑粒子法在模拟流体问题时潜在的应力不稳定问题[25,26].传统的光滑粒子法一般采用钟形光滑函数(如三次样条函数和高斯函数等).在粒子附近很小的一个区域内,当压强不变时,钟形光滑函数会导致粒子之间的排斥力随着粒子间距的减小而减小,从而导致粒子在这个区域内聚集,即应力不稳定现象.本文使用的双曲型光滑函数不存在这种问题,因为当压强不变时,排斥力会随着粒子间距的减小而增大,从而防止粒子聚集,消除应力不稳定问题.

本文使用纳维-斯托克斯方程作为流体的控制方程,其拉格朗日形式为:

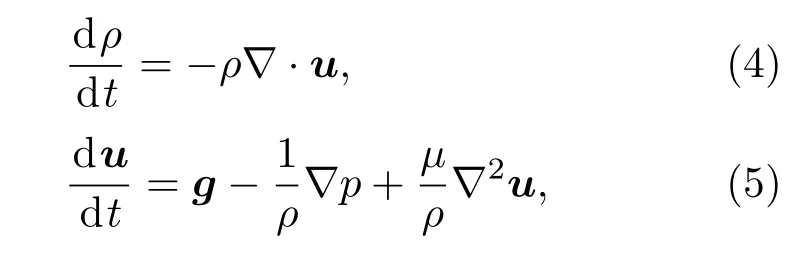
其中ρ,u,p,µ分别表示流体的密度、速度、压强和黏性系数;g表示重力加速度.

在光滑粒子法中,密度方程(4)可以离散成如下形式:

其中∇aWab表示以粒子a为中心的光滑函数在粒子b处的梯度.对于密度差较大的多相流,方程(6)会高估密度大的流体粒子对密度小的流体粒子的贡献.因此,在计算交界面处的大密度粒子对小密度粒子的作用时,采用如下形式的密度方程:

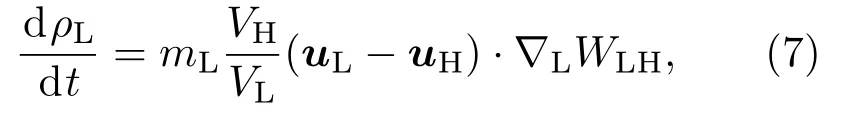
其中脚标H和L分别表示密度大的流体和密度小的流体.与方程(6)相比,上式可以有效地处理大密度比多相流的交界面,降低交界面处的计算误差,并有助于得到清晰光滑的交界面.需要注意的是,对于同相粒子之间的相互作用,以及小密度粒子对大密度粒子的作用,仍使用方程(6)计算.

动量方程(5)中的压力梯度项可离散成(9)式得到的黏性一般会比真实的物理黏性稍小,可以通过人工黏性进行补偿.本文采用如下形式的人工黏性[27]:

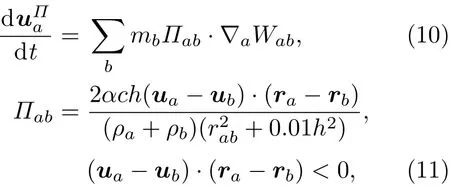
其中参数α用于控制人工黏性的大小,本文取值为α=0.02.人工黏性(11)仅在相邻粒子相互靠近时起作用.另外,人工黏性还能在一定程度上降低粒子的非物理振动[27].

为了防止交界面两侧的粒子相互穿透,并得到光滑清晰的交界面,当不同相的两个粒子相互作用时,在它们之间施加如下形式的排斥力[28−30]:

其中参数εR的取值范围为0—0.1,本文取值为0.02.该排斥力的形式实际上是由压强梯度项的离散形式(8)式演变而来,不同的是,该斥力的值远小于压强梯度,而且只在不同相的粒子之间起作用,即在交界面两侧的粒子之间施加排斥力,从而抑制粒子穿透交界面.另外,该排斥力在一定程度上也能起到表面张力的作用.

控制方程(4)和(5)不封闭,可通过如下状态方程来计算压强:

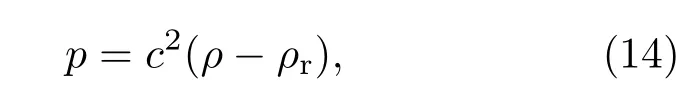
其中c表示数值声速,ρr表示参考密度.

在光滑粒子法中,压强通常会产生较大的非物理波动.为了降低压强波动,一般可以通过密度重置来实现.本文采用如下形式的密度重置方程[31],每20个时间步修正一次密度:

对于粒子的位置移动,采用XSPH运动方式[27]:

其中参数ε的取值范围为0—1,本文取值为0.5.(16)式的求和范围是同相的相邻粒子.另外,在求解密度方程时,也改用速度u′[32],其他方程中的速度仍采用原速度u.

3 单模态瑞利-泰勒不稳定问题

图1是单模态瑞利-泰勒不稳定问题的示意图,其中计算区域的高度为H=2,宽度为L=1,交界面初始形状为y=1−0.15 sin(2πx),上层流体密度为ρH=1.8,下层流体密度为ρL=1.0,重力加速度为g=1.两种流体的动力黏性系数相等:νH= νL=0.0025.Atwood数为At=2/7.所有边界都是刚性无滑移固体壁面条件.初始时刻,整个系统处于静止状态.然后,在重力的作用下,上层重的流体开始向下运动,而下层轻的流体则向上运动.

图1 单模态瑞利-泰勒不稳定问题的初始设置Fig.1.Initial set-up for single-Mode Ray leigh-Tay lor instability p rob lem.

为了验证本文提出的多相流光滑粒子法方法,图2对比了本文的模拟结果和文献中的几种结果.图2中本文模拟结果采用的空间分辨率为200×400,其他结果采用的空间分辨率分别是Levelset 312×624[29];Grenier等[29]300×600;Chen等[33]200×400,Monaghan和Rafiee[34]150×300;Hu和AdaMs[35]60×120.图2表明各种模拟结果中交界面的整体结构大致相似,但局部结构差别较大,例如Chen等[33]与Hu和Adams[35]的交界面不清晰,交界面附近不同种类的流体粒子相互穿透的现象非常明显,而且局部的复杂变化没能模拟出来.Monaghan和Rafiee[34]的交界面比较清晰,但局部的复杂变化也没能模拟出来.相对而言,本文的结果与Level-set和Grenier等[29]的结果不但交界面清晰,而且局部细节丰富.

图2 (网刊彩色)本文结果与文献中结果的对比(t=5)Fig.2.(color online)CoMparison of the resu lts of this paper and literature(t=5).

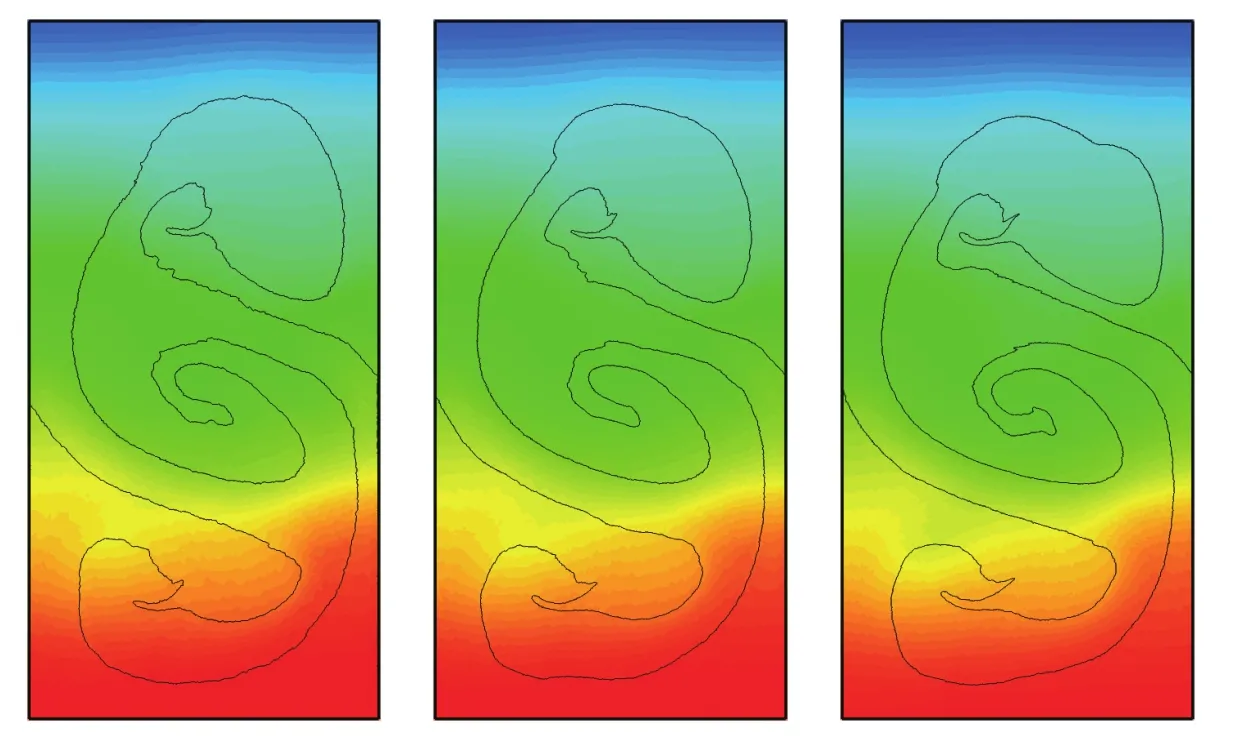
图3 (网刊彩色)三种空间分辨率的模拟结果对比:200×400(左),300×600(中),400×800(右)Fig.3.(color on line)CoMparison of siMu lating resu lts using three diff erent resolutions:200×400(left),300×600(Midd le),400×800(right).

需要指出的是,图2中各种模拟结果采用的空间分辨率虽然并不完全相同,但差别不大,只有Hu和AdaMs[35]的分辨率明显偏低.图3对比了本文方法采用三种分辨率模拟的结果.从图3可以看出,随着分辨率的增加,交界面变得更加光滑,而且细节增多,但是这种变化并不显著.因此,分辨率会影响模拟结果,但并不是导致图2中不同模拟结果的主要原因.图3中的颜色表示流体压强,可以看出,本文方法得到的压强分布不但整体上光滑,而且交界面和壁面附近的压强也是连续的,没有出现异常现象.本文模拟结果的交界面提取方法见文献[36],该方法先以粒子为顶点构建三角形网格,然后在网格上提取交界面.

图4给出了时间t=1,3,5和7时的交界面形态.图5给出了与图4相对应的几个时刻的整个流场中涡的结构.从图4可以看出,交界面从初始时刻的简单形状逐渐演化成非常复杂的形状.从图5可以看出,流场中的涡结构也随着交界面形态的变化而变得逐渐复杂,且涡的数量也随之增加.流体的运动产生涡,同时,涡也反过来影响流体的运动.初始阶段,上层流体从左侧向下运动,下层流体则从右侧向上运动,形成一个逆时针的大涡,并在左右壁面附近形成两个顺时针的小涡(见图5,t=1).这三个涡的中心几乎在同一条直线上.随着两种流体的相互贯穿,在三个涡的作用下,交界面形成了方向相反的两个“蘑菇”状结构(见图4和图5,t=3).三个涡都位于“蘑菇”结构的边沿处,并逐渐增大.同时,在右上角新形成一个顺时针的小涡.由于这个小涡与右中部的涡相互靠近,并且方向相同,最终被吞并,形成一个大涡.在右侧涡的挤压作用下,中间的大涡在左上方分裂出一个小涡.与此同时,左侧原有的涡向下运动,并逐渐增大,占据了下方的位置,而且也分裂出一个小涡(见图5,t=5).值得注意的是,尽管原先的三个涡都改变了位置,且经历了合并或分裂过程,但它们的中心位置依然保持在几乎同一条直线上.最后,到t=7时,因为两种流体在底部的剪切作用,导致了Kelvin-Helmholtz不稳定现象,在底部形成了三个逆时针旋转的小涡.

图4 (网刊彩色)单模态瑞利-泰勒不稳定交界面的演化过程(t=1,3,5,7)Fig.4.(color on line)Evolu tion of interface for single-Mode Ray leigh-Tay lor instability p rob lem(t=1,3,5,7).

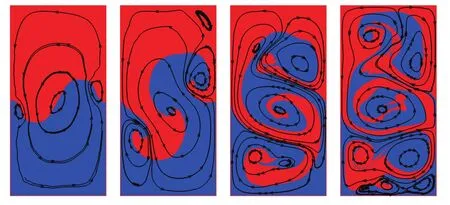
图5 (网刊彩色)与图4对应时刻的涡结构的演化过程(t=1,3,5,7)Fig.5.(color on line)Evolution of vortices at the saMe tiMe of Fig.4(t=1,3,5,7).

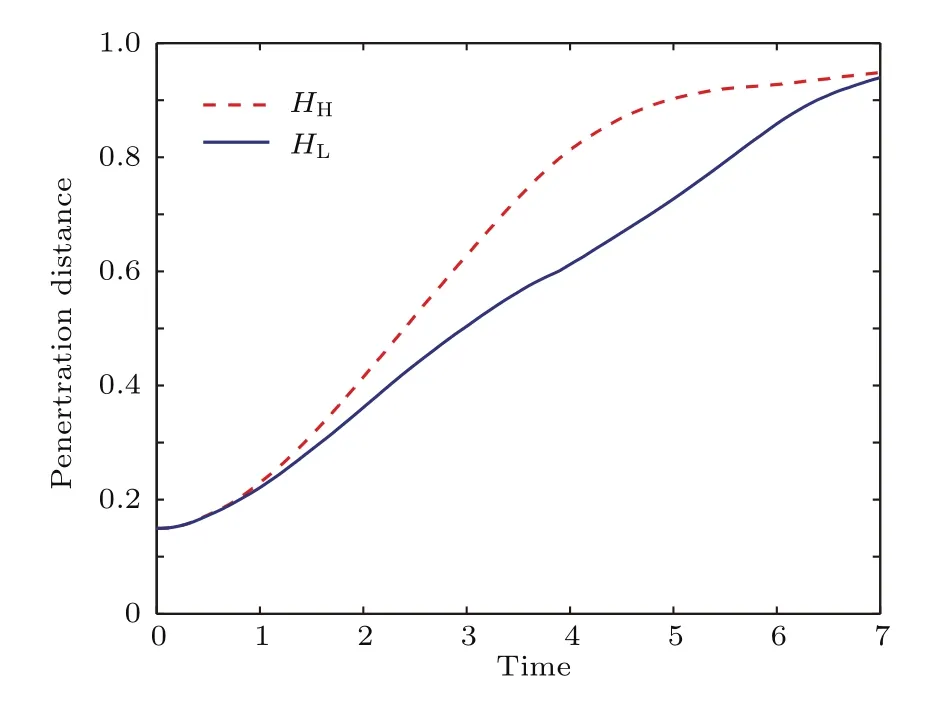
图6 单模态瑞利-泰勒不稳定交界面贯穿深度随时间的变化(HH表示上层重的流体向下进入轻的流体的贯穿深度;HL表示下层轻的流体向上进入重的流体的贯穿深度)Fig.6.Penetration distance as a function of tiMe for single-Mode Ray leigh-Tay lor instability interface(HHis the distance of the heavy fl uid penetrating into the light fl uid;HLis the distance of the light fl uid penetrating into the heavy fl uid).

图6给出了两种流体的贯穿深度随时间的变化过程.图6中纵坐标0表示高度方向的中点,而1则表示上下两端的壁面.从图6可以看出,初始阶段t＜1时,两种流体离开中点的距离几乎同步增加.在t=1之后,重的流体向下运动的速度明显快于轻的流体向上运动的速度.在t=4之后,重的流体已经比较接近底部壁面,因此运动速度迅速降低;而轻的流体因为运动速度较慢,一直到t=6之后才开始降低速度.在t=7时,两种流体已非常接近两端壁面.根据LeWis[3]的实验和Layzer[37]的理论结果,在不考虑壁面影响的情况下,瑞利-泰勒不稳定导致的贯穿深度在初始阶段随时间成指数增加,稳定后随时间成匀速增加关系.在图6中,贯穿深度小于0.3时,约为指数增加阶段,贯穿深度为0.3至0.8时,约为匀速增加阶段.因此,本文的数值结果与LeWis[3]的实验结论及Layzer[37]的理论结果相符.对于贯穿深度大于0.8时,因两端壁面的影响,变为减速阶段.

4 多模态瑞利-泰勒不稳定问题

多模态瑞利-泰勒不稳定问题的初始设置与单模态的设置图1相似,高度为H=2,宽度为L=1.不同的是,多模态问题的交界面形状为y=1−0.05sin(πx/5),上层流体密度为ρH=3,下层流体密度为ρL=1,重力加速度为g=1.两种流体的动力黏性系数相等:νH=νL=0.001.Atwood数为At=0.5.上下两端为刚性无滑移固体壁面条件,左右边界为周期边界条件.

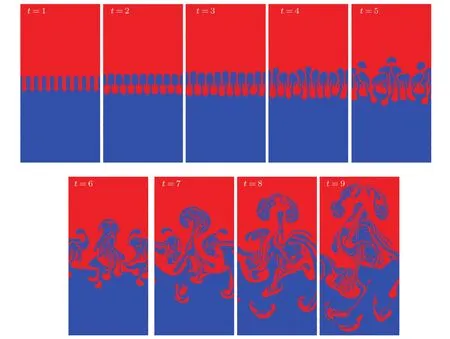
图7 (网刊彩色)多模态瑞利-泰勒不稳定交界面的演化过程Fig.7.(color on line)Evolution of interface forMulti-Mode Ray leigh-Tay lor instability p rob lem.

图8 平均密度随高度的变化(t=3,5,7)Fig.8.Average density as a function of height(t=3,5,7).

图7给出了多模态瑞利-泰勒不稳定交界面的演化过程.初始阶段,初始扰动的波形被逐渐拉长,相邻结构的影响很小 (见图7,t=1).随着贯穿深度的增加,相邻结构相互影响,形成蘑菇状结构(见图7,t=2和3).随着蘑菇状结构的增大,相邻结构的相互作用也加剧,交界面整体结构的对称性被打破,有的蘑菇状结构被拉长,有的蘑菇状结构被压扁(见图7,t=4).然后小尺度结构相互合并,形成不同尺度的大结构 (图7,t=5—9).交界面的形态也随之变得异常复杂.

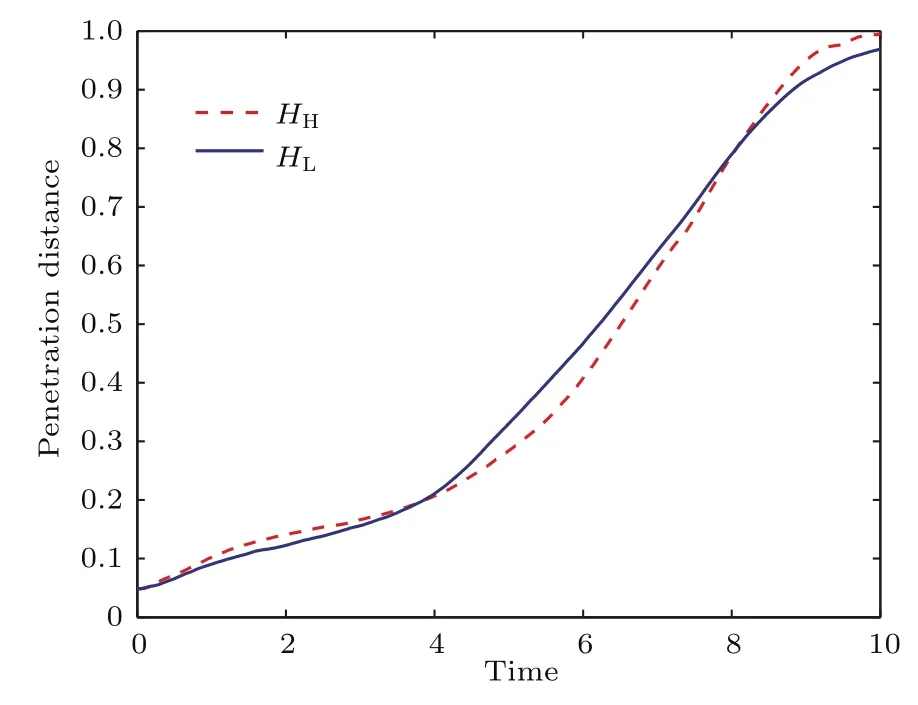
图9 多模态瑞利-泰勒不稳定交界面的贯穿深度随时间的变化(HH表示上层重的流体向下进入轻的流体的贯穿深度;HL表示下层轻的流体向上进入重的流体的贯穿深度)Fig.9.Penetration d istance as a function of tiMe for Mu lti-Mode Ray leigh-Tay lor instability interface(HHis the d istance of the heavy fl uid penetrating into the light fl uid;HLis the distance of the light fl uid penetrating into the heavy fl uid).

图8是水平方向的平均密度随高度的变化情况.在t=3时,流体的贯穿深度相对较小,交界面形状也比较规则,所以平均密度的变化比较规则.到t=5时,密度出现了不同尺度的变化,这是因为交界面的小结构已逐渐合并成不同尺度的大结构,而这种结构尺度的变化也体现在了平均密度的变化上.无规则的尺度变化逐渐加剧,到t=7时,已经完全看不出初始阶段的规则变化.

图9给出了两种流体相互贯穿的深度随时间的变化情况.从图9可以看出,两条线的形状相似.初始阶段,贯穿深度的增加稍快,而后缓慢增加.在t=4附近,穿透距离加速增加,而后几乎线性增加.这是因为,原先的小“泡”开始合并成大“泡”,而大“泡”的运动速度大于小“泡”.当贯穿深度到达0.9附近时,因为上下两端壁面的作用,贯穿深度趋于稳定,贯穿速度迅速降低.

5 结 论

本文在传统光滑粒子法的基础上发展了一种适用于模拟多相流的光滑粒子法,并应用该方法模拟研究了单模态和多模态瑞利-泰勒不稳定问题.该方法对密度方程在交界面处的离散格式进行了修正以适应多相流所涉及的大密度比情况,在不同相粒子之间施加了很小的排斥力以防止粒子穿透交界面,并采用了最新发展的双曲型光滑函数以消除应力不稳定问题.为了验证本文发展的多相流光滑粒子法,将本文与文献中的几种模拟结果进行了对比.结果表明,在模拟瑞利-泰勒不稳定问题时,本文方法的结果明显优于文献中的大部分光滑粒子法模拟结果,与文献[29]的结果相当,但本文方法比文献[29]的方法更简单方便.

对于单模态瑞利-泰勒不稳定问题,给出了交界面的形态及涡结构的演化过程,并研究了贯穿深度与时间的关系.贯穿深度随时间的变化过程与实验及理论结果相符.对于多模态瑞利-泰勒不稳定问题,研究了交界面演化过程中小尺度结构合并成大尺度结构的过程.在此过程中,水平方向的平均密度随高度的变化由初始时的规则分布逐渐演化成无规则分布.小尺度结构向大尺度结构的演化也导致了贯穿深度随时间的增加速度由线性改变成非线性.合并过程结束后,贯穿深度再次与时间成线性关系,但是增加速度明显大于合并前的增加速度.

[1]Ray leigh L 1883 Proc.Lond.Math.Soc.14 170

[2]Tay lor G 1950 Proc.Roy.Soc.A:Math.Phys.201 192

[3]LeWis D J 1950 Proc.Roy.Soc.A:Math.Phys.202 81

[4]Tryggvason G 1988 J.CoMput.Phys.75 253

[5]Banerjee R,K an jilal S 2015 J.Pure App l.Ind.Phys.5 73

[6]Sharp D H 1984 Physica D 12 3

[7]K ilkenny J,G lendinning S,Haan S,HamMel B,Lind l J,Mun ro D,ReMington B,Weber S,Knauer J,Verdon C 1994 Phys.P lasMas 1 1379

[8]Huang C S,Kelley M,Hysell D 1993 J.Geophys.Res.-Space Physics 98 15631

[9]A lon U,Hecht J,O fer D,Shvarts D 1995 Phys.Rev.Lett.74 534

[10]DiMonte G 2000 Phys.P lasMas 7 2255

[11]RaMshaWJ D 1998 Phys.Rev.E 58 5834

[12]G limMJ,Saltz D,Sharp D H 1998 Phys.Rev.Lett.80 712

[13]Cheng B,G limMJ,Sharp D 2002 Phys.Rev.E 66 036312

[14]Zhang Y S,He Z W,Gao F J,Li X L,T ian B L 2016 Phys.Rev.E 93 063102

[15]He X,Chen S,Zhang R 1999 J.CoMput.Phys.152 642

[16]Kadau K,Barber J L,GerMann T C,Holian B L,A lder B J 2010 Phil.Trans.R.Soc.A 368 1547

[17]RaMap rabhu P,K arkhanis V,Banerjee R,Varshochi H,K han M,LaWrie A 2016 Phys.Rev.E 93 013118

[18]Sagert I,Howell J,Staber A,Strother T,Colbry D,Bauer W2015 Phys.Rev.E 92 013009

[19]Liang H,Li Q,Shi B,Chai Z 2016 Phys.Rev.E 93 033113

[20]Lucy L B 1977 Astron.J.82 1013

[21]G ingold R A,Monaghan J J 1977 Mon.Not.R.Astron.Soc.181 375

[22]Yang X,Peng S,Liu M,Shao J 2012 In t.J.CoMp.Meth.-Sing 9 1240002

[23]Yang X F,Peng S L,Liu MB 2014 Appl.Math.Model 38 3822

[24]Yang X,Dai L,Kong SC 2017 Proc.CoMbust.Inst.36 2393

[25]Yang X F,Liu MB 2012 Acta Phys.Sin.61 224701(in Chinese)[杨秀峰,刘谋斌 2012物理学报 61 224701]

[26]Yang X F,Liu MB,Peng S 2014 CoMput.F luids 92 199

[27]Monaghan J J 1992 Ann.Rev.Astron.Astrophys.30 543

[28]Monaghan J J 2000 J.CoMput.Phys.159 290

[29]G renier N,Antuono M,Colagrossi A,Le TouzéD,A lessand rini B 2009 J.CoMput.Phys.228 8380

[30]Yang X,Liu M2013 Sci.China:Phys.Mech.Astron.56 315

[31]Bonet J,Lok T S 1999 CoMput.Methods App l.Mech.Engrg.180 97

[32]Colagrossi A,Land rini M2003 J.CoMput.Phys.191 448

[33]Chen Z,Zong Z,Liu M,Zou L,Li H,Shu C 2015 J.CoMpu t.Phys.283 169

[34]Monaghan J,Rafiee A 2013 In t.J.NuMerical Mech.F luids 71 537

[35]Hu X Y,AdaMs N A 2009 J.CoMput.Phys.228 2082

[36]Yang X F,Liu MB 2016 Chin.J.CoMput.Mech.33 594(in Chinese)[杨秀峰,刘谋斌 2016计算力学学报 33 594]

[37]Layzer D 1955 Astrophys.J.122 1

PACS:47.20.–k,47.11.–j,68.05.–nDOI:10.7498/aps.66.164701

*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.11302237,U 1530110).

†Corresponding author.E-Mail:mb liu@pku.edu.cn

N uMerical study of Ray leigh-Tay lor instab ility by using sMoothed particle hyd rodynaMics∗

Yang Xiu-Feng1)Liu Mou-Bin2)†

1)(DepartMent ofMechanical Engineering,Iowa State University,AMes,IA 50011,USA)
2)(BIC-ESAT,College of Engineering,Peking University,Beijing 100187,China)

1 Ap ril 2017;revised Manuscrip t

2 June 2017)

In this paper,we present a sMoothed particle hydrodynaMics(SPH)Method for Modeling multiphase floWs.The multiphase SPH method includes a corrective discretization scheme for density app roximation around the fl uid interface to treat large density ratio,a sMall repulsive force between particles froMdiff erent phases to p revent particles froMunphysically penetrating fluid interface,and a neWly-developed hyperbolic-shaped kernel function to remove possible stress instability.This mu ltiphase SPH Method is then used to study the single-and multi-Mode Rayleigh-Taylor instability p robleMs.A coMparison between our results With the resu lts froMexisting literature shoWs that our results are obviously better than most available results froMother SPH simulations.The present results are close to those by G renier et al.while the present multiphase SPH Method is siMp ler and easier to iMp leMent than that in the work by G renier et al.(G renier,et al.2009 J.CoMput.Phys.228 8380).For the single-Mode Rayleigh-Tay lor instability,the evolutions of the interface pattern and vortex structures,and the penetration depth each as a function of time are investigated.For themu lti-Mode Rayleigh-Tay lor instability,theMerging of sMall structures into a large structure during the evolution of the interface is studied.The horizontal average density and the penetration each as a function of height are also studied.

Rayleigh-Taylor instability,smoothed particle hydrodynaMics,multiphase flow

10.7498/aps.66.164701

∗国家自然科学基金(批准号:11302237,U 1530110)资助的课题.

†通信作者.E-Mail:Mb liu@pku.edu.cn

©2017中国物理学会C h inese P hysica l Society

http://Wu lixb.iphy.ac.cn