基于经验模态分解和径向基函数网络的汇率预测

文/邓生财 陈卓

基于经验模态分解和径向基函数网络的汇率预测

文/邓生财 陈卓

为提高非线性外汇交易的预测精度，本文提出了一种基于经验模态分解和径向基函数网络结合的预测方法，并通过绝对误差、均方误差和相关系数指标来评估提出模型的性能。首先对原始汇率数据进行经验模式分解，得到若干个平稳的本征模态函数和一个残差向量，然后用径向基函数网络分别对分解后的每个分量进行预测，最后对各分量预测进行求和，求和值作为预测结果。本论文以美元对人民币交易案例为研究对象，实验结果表明，与单一的径向基函数网络模型相比，基于经验模式分解和径向基函数网络结合的预测方法具有更高的预测精度。

外汇交易；汇率预测；经验模态分解；径向基函数网络

1.引言

汇率的波动会对国内的通货膨胀[1]和进出口[2]等产生一定的影响。而利用历史汇率数据，构造相应的预测模型来预测未来的汇率变化，可以防患于未然。传统的股票时间序列预测方法有指数平滑法[3]自回归滑动平均模型[4]等。这些模型对线性时间序列的预测可获得良好的效果，但在实际应用中，大多数的时间序列具有不稳定和非线性等特征。为此，基于非线性特征的支持向量机[5]和神经网络预测模型[6]被相继提出，并在股票预测方面取得了较好成果。由于股票受到各方面因素的影响，使序列变得复杂而难以预测，倘若单一地使用这些方法来进行股票时间序列的预测，会使训练陷入局部最优，而难以达到满意的效果，因此具有一定的局限性。为解决这个问题，本文提出了一种基于经验模态分（EMD）和径向基函数网络（RBF）结合的方法，来预测美元兑人民币的汇率。该方法具有以下几点优势：（1）因为时间序列具有不稳定和非线性等特点，首先利用EMD方法对原始汇率数据进行处理，可以使得原始信号更平稳，降低外界噪音对预测的影响；（2）RBF神经网络训练速度快，且具有全局最优的特点，克服了BP神经网络陷入局部最优的情况，从而获得更高精度的预测结果；（3）本文还对实验结果进行了最优参数的挖掘与分析，以获得最佳的预测结果。

本文的剩余部分组织如下：第2部分分别介绍了EMD和RBF网络的理论并建立了EMD-RBF预测模型；第3部分进行了案例分析与参数挖掘；第4部分得出了实验结论。

2.基于经验模式分解和径向基函数网络的预测模型

2.1 经验模态分解

经验模态分解方法[7]是黄锷等人在1998年提出的一种新型自适应信号时频处理方法，适用于非线性、非平稳信号的分析处理。经验模态分解方法是依据数据自身的时间尺度特征来进行信号分解。该方法能使复杂信号分解为若干个本征模函数和一个残差。所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号，残差从某种程度上代表着原始信号的趋势。分解出来的IMF必须满足以下两个条件：

（1）在全部时间序列观测点中，极值点的个数必须要与零交叉点的个数相等或者最多相差一个。

（2）在任意一点上，由局部极大值形成的上包络线和局部极小值形成的下包络线求得的均值为零。

通常，大多数要分析的时间序列并不是IMF，往往包含一个或多个震荡模式。因此，需要对数据进行EMD分解，以获得IMF。EMD分解必须满足以下三个条件：

（1）信号必须有两个极值，一个极大值和一个极小值。

（2）通过极值之间的跨度确定特征时间尺度。

（3）如果数据没有极值点但包含拐点，可以通过对它进行一次或多次微分来求得极值。

EMD分解原始信号，其实就是信号筛选的过程。原始信号通过EMD方法分解得到若干个IMF和一个残差向量。信号筛选步骤如下所示：

第一步：绘制上、下包络线。找到原始信号x（t）中的所有极大值点max和极小值点min，并利用三次样条插值方法分别绘制出上、下包络线。

第二步：计算上下包络线对应各点的均值m1。

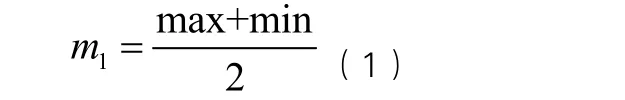
第三步：计算原始信号x（t）和均值m1的差值d1。

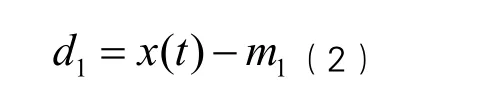
第四步：理论上d1应该是一个IMF，但大多数情况下d1不满足IMF的特性，因此用d1替代原始信号，重复步骤1，2和3进行s次筛选，以分解出第一个IMF，用c1表示。

第五步：设置筛选停止条件。用标准方差SD来控制，其计算公式如下所示：

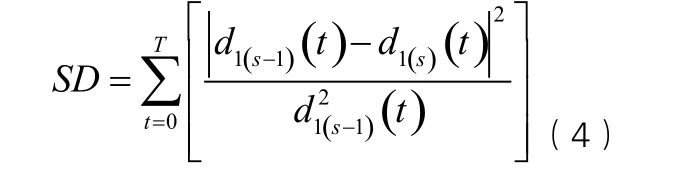
按照经验，SD一般取值在0.2到0.3之间。

第六步：计算剩余信号r1。

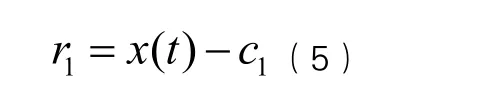
第七步：一般情况下，r1仍然还包含着多个内在的震荡模式，故把r1当成信号，继续上述分解筛选过程，直到不能分解为止，其结果可表示为：

第八步：当满足以下任意一个条件时，筛选过程会停止：

（1）当cn或rn小于预先设定的的值时，筛选过程停止。

（2）当余量rn是单调函数或者不能再提取出IMF时，筛选过程停止。

原始信号x（t）经过n次筛选，分解出来了n个IMF和一个残差，对原始信号重构有：

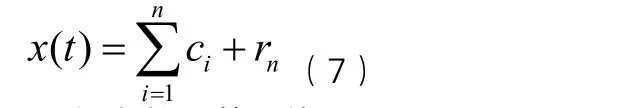
2.2 径向基函数网络

RBF是由Moondy等在20世纪80年代提出的一种具有单隐藏层的三层前馈网络。它能以任意精度逼近任意非线性函数，在一定程度上克服了BP神经网络学习速度慢，训练时间长，参数调节多等缺点。由于RBF网络具有能够逼近任意的非线性函数，处理系统内的难以解析的规律性和良好的泛化能力等特点，所以在模式识别、经济预测等领域被广泛应用。RBF网络的分布函数为：

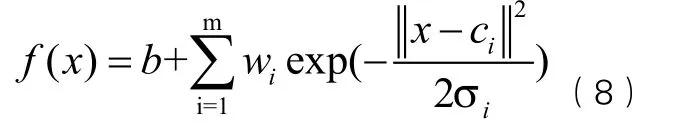
其中i表示输入数据，b表示偏置，m表示基函数个数，即为隐藏层神经元数目，w为连接权重，gi（.）为隐藏层第i个神经元的径向基函数，为欧几里得范数，σ为基函数的扩展常数，控制函数的径向作用范围。

2.3 EMD-RBF模型构建

构建的EMD-RBF模型，首先对原始汇率交易数据进行EMD变换，然后再使用RBF神经网络来训练预测模型。具体的实验步骤如下所示。

第一步：加载数据并对数据预处理，设数据长度为L。

第二步：对处理好的外汇数据进行EMD变换，分解出n个分量，分别是：（n-1）个IMF和1个残差向量。

第三步：分别对每个IMF和残差向量以时间窗口长度为k生成样本。如第一个样本为第1个数据到第k个数据作为输入，第（k+1）个数据作为目标输出；第二个样本为第2个数据到第（k+1）个数据作为输入，第（k+2）个数据作为目标输出；以此类推，故每个分量都可生成（L-k）个样本。

第四步：分别随机选取每个分量的q个样本作为训练样本来分别训练每个RBF网络，剩余的样本作为测试样本。

第五步：把测试样本输入对应训练好的RBF网络中，进行仿真预测，并对每个RBF网络输出的预测值求和，求和值作为最终预测值。

第六步：模型性能评价：为了验证模型的可靠性，本文选择平均绝对误差（MAE）、均方误差（MSE）作为模型性能的评价指标。它们的计算公式分别如下所示：

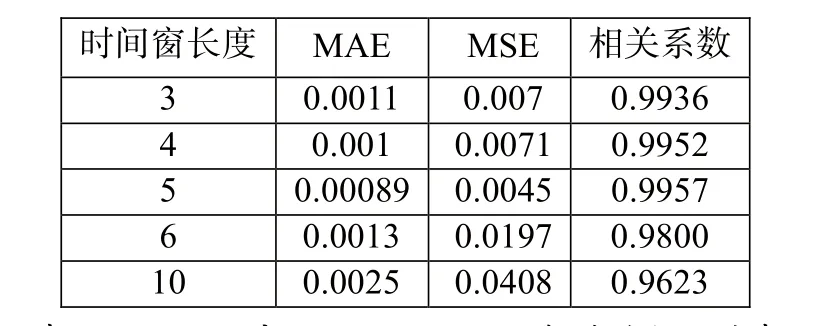
表1 不同时间窗的MAE、MSE和相关系数统计表

其中（i=1，2，3…51），n表示样本的数量，xi表示第i个样本真实输出值，表示样本真实值得均值，yi表示第i个的样本的网络预测输出值，表示预测值的均值。计算出的MAE和MSE的值越小，则表明预测结果越准确，预测模型就越可靠。

3.案例分析

在本小节，以美元兑换人民币为案例研究对象，对提出的模型进行性能评估。使用的数据为美元兑换人民币的日汇率值，时间从2013年1月2日到2016年6月1日，共855个该数据，其来源于http：//fx.sauder.ubc.ca/data.html。

首先对交易数据进行EMD分解，分解结果如图1所示，然后采用径向基函数网络来训练。

由于在适当范围内，不同样本长度（即输入神经元的个数）的选择会对实验结果产生重要的影响，并且径向基函数的密度常数越大，网络预测的性能也越好，因此选择出最优的参数组合就显得尤为重要。所以，本文通过多次实验来确定最合适的时间窗长度和最优的密度常数参数，并依据Eq.（9），Eq.（10），Eq.（11）来分析实验结果和验证模型的准确性与可靠性。

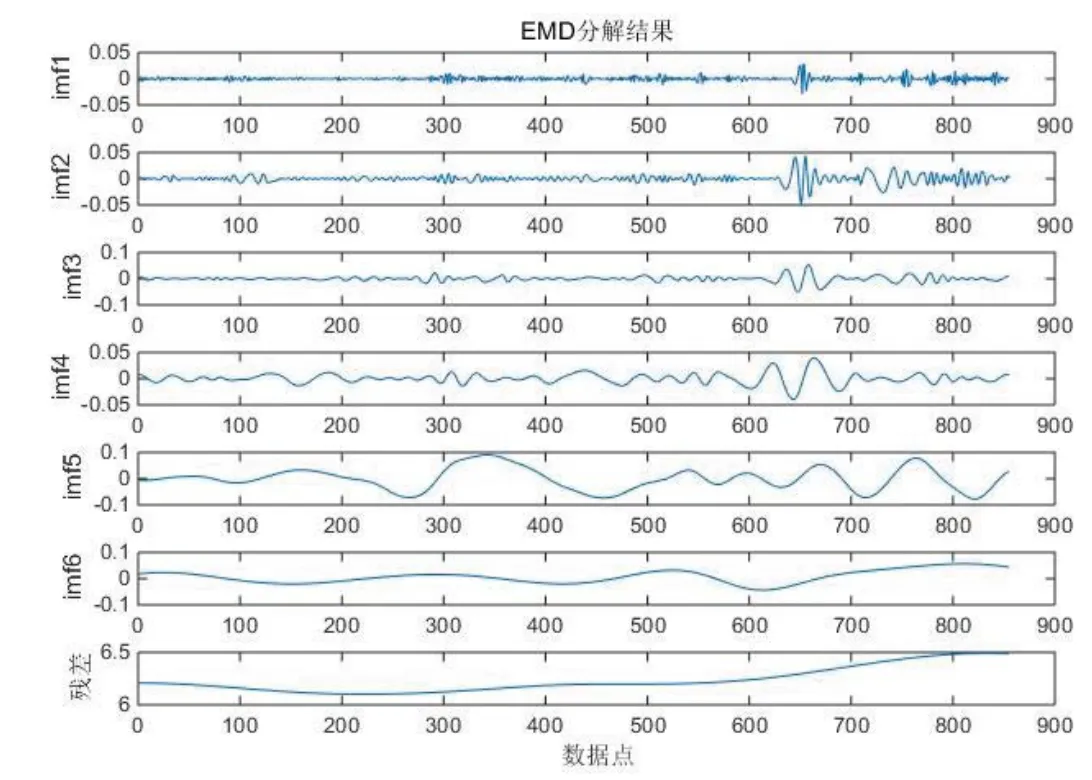
图1 EMD分解结果

3.1 最优时间窗长度

选择不同时间窗长度的数据来训练模型并预测下一次的汇率，会对预测模型的准确性产生重要的影响，这部分通过试探实验，分别设定时间窗口长度为3、4、5、6、10这五个参数，并分别计算它们的MAE、MSE和与原外汇序列的相关系数R，来确定最优的时间窗口长度。

由表1知，当时间窗长度由3、4到5时，实验所获得的MAE和MSE在减小，这说明预测模型具有更准确的预测能力；当时当时间窗长度由5、6到10时，实验所获的MAE和MSE在增大，这表明，预测模型的准确性在下降。也由表1知，时间窗长度由3增加到5时，预测所得序列与真实序列的相关性呈现正相关的关系；由时间窗长度5增加到10时，预测序列与真实序列的相关性呈负相关关系。这再一次验证了，当取时间窗长度为5时，可以获得最佳的实验效果。

3.2 最优密度常数

这部分是在时间窗长度为5的情况下，通过计算单一RBF网络预测模型和EMD-RBF预测模型这两种模型分别在密度常数参数为2、3、4和5这四组常数下的MAE、MSE这两个个指标来确定预测模型的最优密度常数。

表2 不同密度常数的MAE与MSE统计表

由表2知，在密度常数为5时，RBF网络预测所得的最小MAE为0.0072，最小MSE为0.0242。而EMD-RBF模型预测所得的最小MAE和最小MAE在密度常数为3时获得，它们分别为0.0029和0.0013。故表明，单一的RBF网络最优密度常数为5，EMD-RBF预测模型最优密度常数为3。

综上所述，由于在各预测模型最优参数设置下，EMD-RBF预测模型计算得到的MAE和MSE都是最小的，这表明，基于EMD-RBF的外汇汇率预测较单一的RBF网络预测具有更稳定和更可靠的特点。

4.结论

本文提出了基于EMD-RBF预测模型方法来预测美元兑换人民币的外汇时间序列，首先对数据进行EMD分解得到若6个IMF和1个残差向量，然后把IMF和残差分别输入RBF网络进行预测，最后对相应的每个预测结果求和作为预测值。通过美元兑人民币的案例研究，可得出如下结论：（1）通过EMD-RBF模型预测，所获得的最小MAE和MSE都小于单一使用RBF网络预测所获得的MAE和MSE；（2）基于EMD-RBF模型进行美元兑人民币外汇时间序列的预测比基于RBF径向基函数网络进行外汇时间序列预测更高的准确性和可靠性。因此该预测模型在实际应用中具有一定的参考价值。本文只是对汇率进行单步预测，在以后的研究中，将对外汇数据进行多步预测的建模和验证分析，以提高该预测模型的适用范围。

（作者单位：重庆工商大学电子商务与供应链系统重庆市重点实验室）

[1]王家玮，孙华妤，门明. 人民币汇率变动对通货膨胀的影响——基于进口非竞争型投入产出表的分析[J]. 国际金融研究，2011（10），30～39.

[2]谭小芬，王雅琦，卢冰. 汇率波动、金融市场化与出口[J].金融研究，2016（3）：15～30.

[3]徐建新，严勇，严复海. 指数平滑法在典型城市GDP预测中的应用[J]. 水利科技与经济，2008，14（17）：551～554.

[4]杨一文，杨朝军. 基于支持向量机的金融时间序列预测.系统管理学报，2005，14（2）：176～181.

[5]杨娟丽，徐梅，王福林等. 基于BP神经网络的时间序列预测问题研究. 数学的认识与实践. 2013，43（4）：158～164.

[6]梁强，范英，魏一鸣. 基于小波分析的石油价格长期趋势预测方法及其实证研究[J]. 中国管理科学，2005，13（1）：30～36.

[7]HUANG N E，SHEN Z. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Royal Society of London Proceedings Series A，1998（454）：903～995.