火电厂机组负荷优化分配的混沌粒子群算法分析

金洪吉

(四川信息职业技术学院电气工程系，四川广元628017)

火电厂机组负荷优化分配的混沌粒子群算法分析

金洪吉*

(四川信息职业技术学院电气工程系，四川广元628017)

火电厂根据每台机组煤耗性能进行最优负荷分配，能够直接降低全厂供电煤耗，有效适应企业竞争和节能减排的需求。基于此，研究验证其中起决定意义的算法分析，考虑阀点效应和实际机组的约束条件，建立了发电机组负荷优化分配的罚函数数学模型;将混沌优化算法和动态惯性权重法与粒子群算法相结合，形成更为科学有效的混沌粒子群算法;运用某电厂3台机组的历史数据进行验证分析，煤耗最大降低0.8 t/h，证明了算法的实际可行性。

火力发电厂;负荷优化分配;混沌粒子群算法;煤耗特性;动态惯性权重

在当前电力行业竞争愈来愈激烈的情况下，火电厂如何降低煤耗、提高经济效益、促进可持续发展具有重要的研究意义。负荷优化分配就是在保证电网安全的条件下，根据全厂主、辅机投运状况和各台机组运行效率及煤耗，研究运用实际可行的最佳算法分析，进行最优化的负荷分配［1］，实现全厂的最大收益。

Kennedy和Eberhart［2-4］等于1995年提出的粒子群优化PSO(Particle Swarm Optimization)算法对目标函数没有限制条件，简单易实现，求解效率高，缺点是易陷入局部最优点、进化后期收敛速度慢。Jiao等提出的动态惯性权重的粒子群算法，能够解决粒子群算法进化后期速度慢的问题;作为一种新型的混沌优化算法，则能解决粒子群算法容易陷入局部最优解的问题［5］。

本文在研究火电厂机组负荷优化分配中，将混沌优化算法和动态惯性权重法与粒子群算法相结合，理论推理与实践验证相结合，推演精准新算法，实现效益最大化。

1 数学模型的建立

火电厂厂级负荷分配给定全厂负荷指令后，各发电机组在出力限制的允许范围内，根据煤耗特性，科学合理分配负荷，使全厂煤耗达到最低。

设一座火力发电厂N台机组投入并联运行，担负的总负荷为D。各发电机组的负荷Pi(1，2，…，N)作为变量，fi(Pi)为第i台机组的标准煤耗量和功率的特性方程。式中，ai、bi、ci为第i组机组的煤耗特性参数;Pi为第i台机组输出功率。

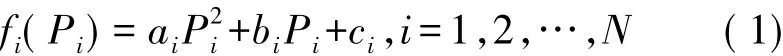
发电机组煤耗特性曲线通过热力实验所获得，以标准供电煤耗作为经济性指标进行研究。电厂中各机组实际运行时，对应能耗特性曲线上会出现波浪起伏状，称为阀点效应。原因就是各个大型的汽轮机发电机组中控制蒸汽供应量的调节阀，打开瞬间，蒸汽量会有所损失。因此，要想获得所需输出，必须在调节阀打开前增加更多蒸汽。

因而，考虑阀点效应后的能耗特性与原先所不同，具体表达式如下所示:

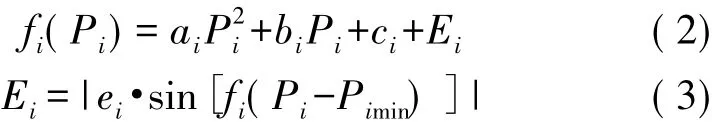
式中，Ei为阀点效应引起的煤耗量特性变化;ei、fi为煤耗特性参数;Pimin为第i台机组输出功率的下限。

全厂总煤耗量F(Pi)作为目标函数，得到方程是:

i=1

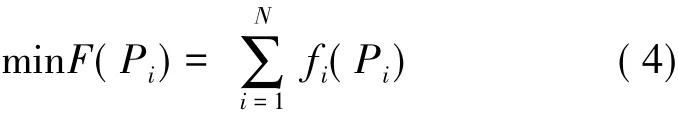
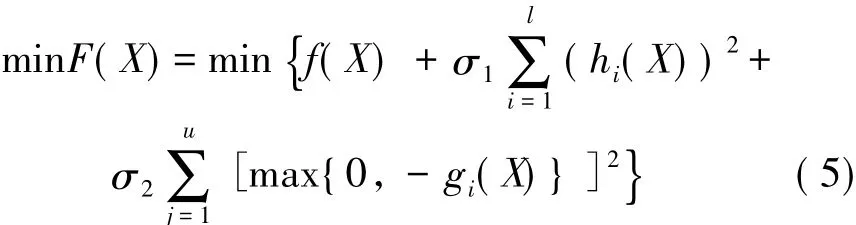
采用构造外点罚函数法，将负荷平衡约束条件计入目标函数中。表达式为:式中，hi(X)=0，i=1，2，…，l;gi(X)≥0，j=1，2，…，u; X=(x1，x2，…，xn)T为待优化向量;l，u分别为原问题等式和不等式约束的个数;σ1，σ2为对应于等式和不等式约束的罚系数。

考虑到系统负荷平衡的约束条件，本文所建立的数学模型如下所示:

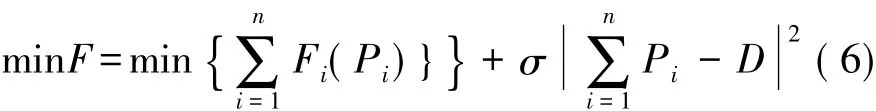
式中，σ为罚系数;n为全厂总机组的个数。

2 火电厂负荷优化分配

2.1 基于混沌粒子群优化算法的机组负荷优化分配流程

首先就电厂厂级负荷优化分配流程描述如下所示，具体流程如图1所示。

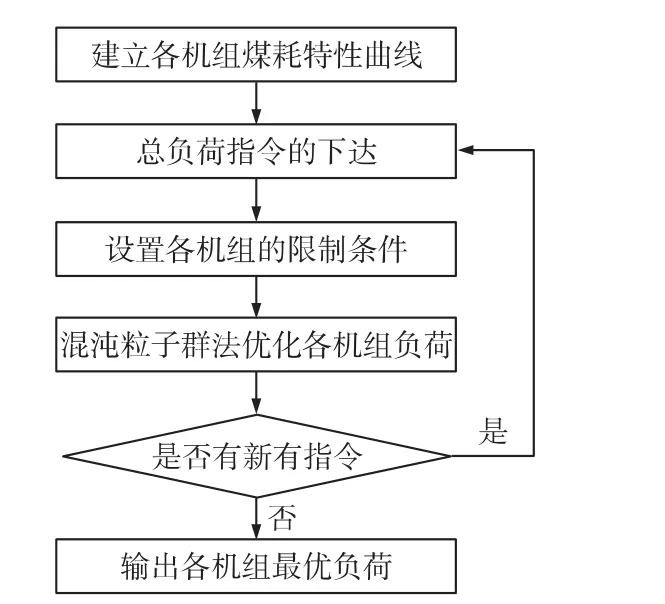
图1 电厂机组负荷优化分配流程图

根据流程图，首先分析各单元机组发电功率的历史数据，通过热力学试验建立各个单元机组发电功率与标准供电煤耗量的函数关系;设置各单元机组发电功率的上限和下限;根据电网调度指令确定全厂机组总负荷指令;采取混沌粒子群法优化各单元机组的负荷，得出最优分配负荷;判断是否有新的调度指令，如有，则继续根据电网调度指令确定全厂机组总负荷指令，否则机组负荷优化分配终止。

2.2 混沌映射及混沌粒子群优化算法

针对2.1节中的混沌粒子群优化算法算法具体论述如下:

Logistic一维映射形式简单，具有复杂的动力学行为，并为保密通信领域广泛应用，数学表达式如下:

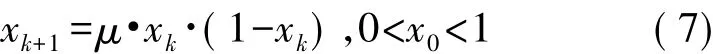
式中，μ为控制参量，取μ为4;且当x0∉{0，0.25，0.5，0.75}时，Logistic完全处于混沌状态。

起初Kennedy和Eberhart提出的粒子群算法是模拟鸟群觅食过程中迁徙和群集行为的演化算法。该算法基于随机搜索理论，对目标函数没有限制条件，通过粒子之间的相互协作来搜寻最优解，每个粒子在迭代过程中通过不断更新粒子的速度和位置来寻找自身和群体的最优值，即极值负荷和最值负荷，其更新公式为:

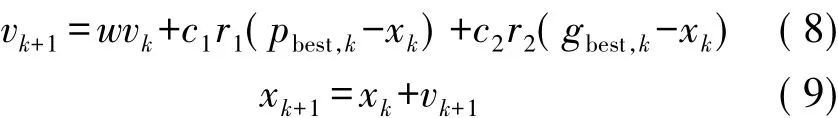
式中，vk为粒子速度;w为惯性权值;c1、c2为学习因子，设为2;r1，r2为介于［0，1］之间的随机数;xk为当前粒子的位置;pbest，k为粒子最优解即机组的极值负荷;gbest，k为种群最优解即机组的最值负荷。

实际应用中，粒子群算法存在局部最优点、收敛速度较慢等缺点。为此，Eberhart和Shi Y［5］对粒子群算法进行改进，引入了动态惯性权重的概念。惯性权重随着迭代次数的增加而逐渐降低，在初始搜索阶段具有较强的全局搜索能力，而在后期较小的惯性权重则收敛于最优解，解决了粒子群算法在进化后期速度慢的问题。将固定的惯性权重改为函数形式w(t)，通过w(t)函数的变化来动态调整粒子群优化算法搜索能力［7-8］。动态惯性权重表达式如式(12)所示:

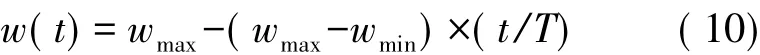
式中，wmax、wmin分别是w的最大和最小值;t、T分别为当前迭代和最大迭代次数，则算法的速度和位置更新公式将变成:

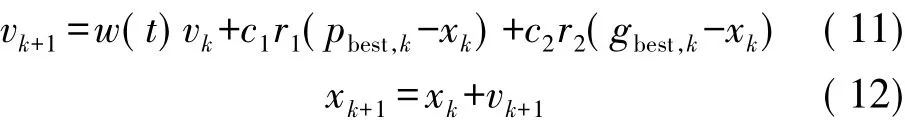
在此基础上，引入混沌优化算法来提高粒子群算法全局搜索的能力［9］，即利用混沌系统特有的随机性和遍历性，帮助粒子逃离局部最优值，并快速收敛于最优解［10-12］。具体方法为，对所有全局最优粒子中随机抽取一维变量进行Logistic映射。

基于混沌粒子群优化算法的步骤如下:

Step 1设置粒子群的初始值，同时调整各机组煤耗特性参数，在限制条件内随机分配各机组负荷;

Step 2利用算法计算各机组负荷的煤耗值，同时做出相应的记录;

Step 3把各负荷的煤耗值与极值负荷的煤耗值做比较，煤耗值较小的，保留其对应负荷，并将该负荷设为极值负荷;

Step 4把各负荷的煤耗值与最优负荷的煤耗值做比较，煤耗值较小的，保留其对应负荷，并将该负荷设为最值负荷;

Step 5由式(10)～式(12)更新种群的负荷值。

Step 6对gbest=(gbest1，gbest2，…，gbestD)全局最优负荷进行混沌优化。

Step 6.1将gbesti(i=1，2，…，D)映射到Logistic方程式即式(9)的定义域(0，1)中，映射方法如式(15)所示:

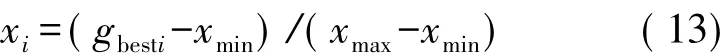
Step 6.2通过Logistic方程即式(14)进行迭代，产生混沌变量变量序列(m=1，2，…)。

Step 6.3把产生的混沌变量序列通过映射后返回到原解空间，映射公式如式(14)所示:

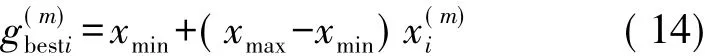
Step 8若满足迭代条件，则停止搜索并输出最优负荷，否则转至Step 2;

3 实验验证及对比分析

利用MATLAB软件平台，编写算法程序，实例验算混沌粒子群算法的可行性。

以某电厂3台发电机组的历史数据为依据，拟合出各台发电机组的性能参数、负荷上下限，详细数据如表1所示;对不同总负荷用混沌粒子群优化算法进行验证计算，并与粒子群算法和平均分配的结果进行比较，优化结果如表2和表3所示;种群规模为190，迭代次数设为610代。

表1 机组煤耗特性方程系数

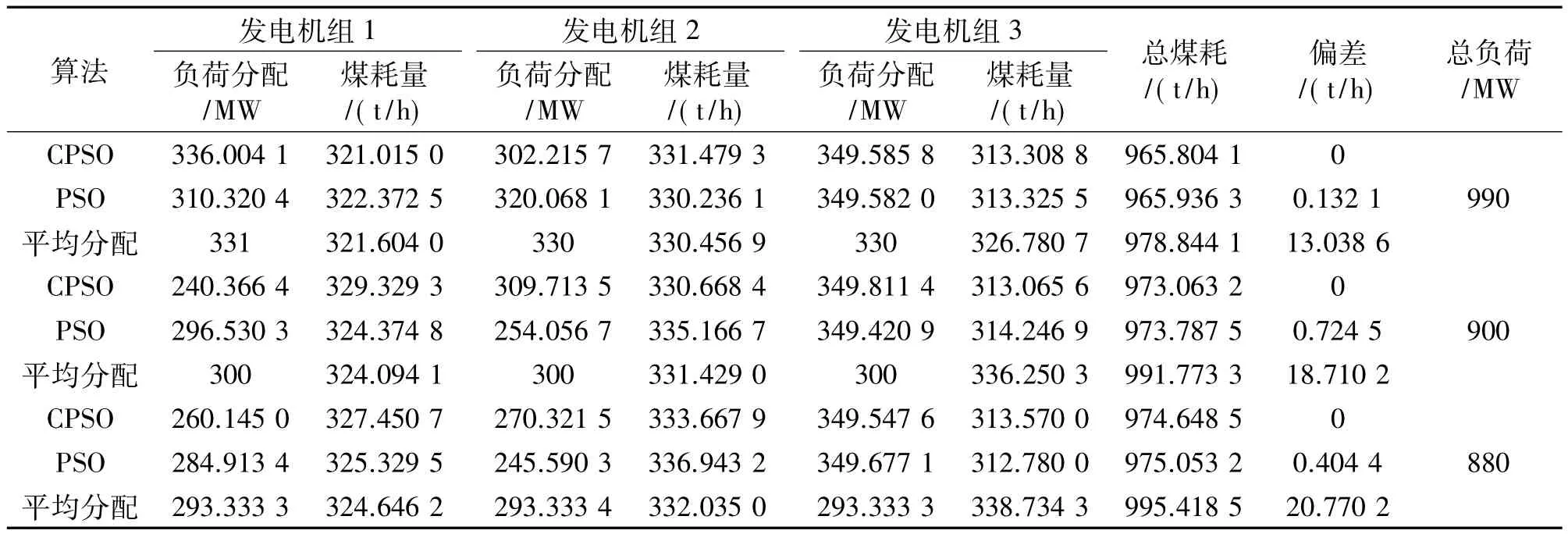
表2 不同总负荷时优化结果(880～990)

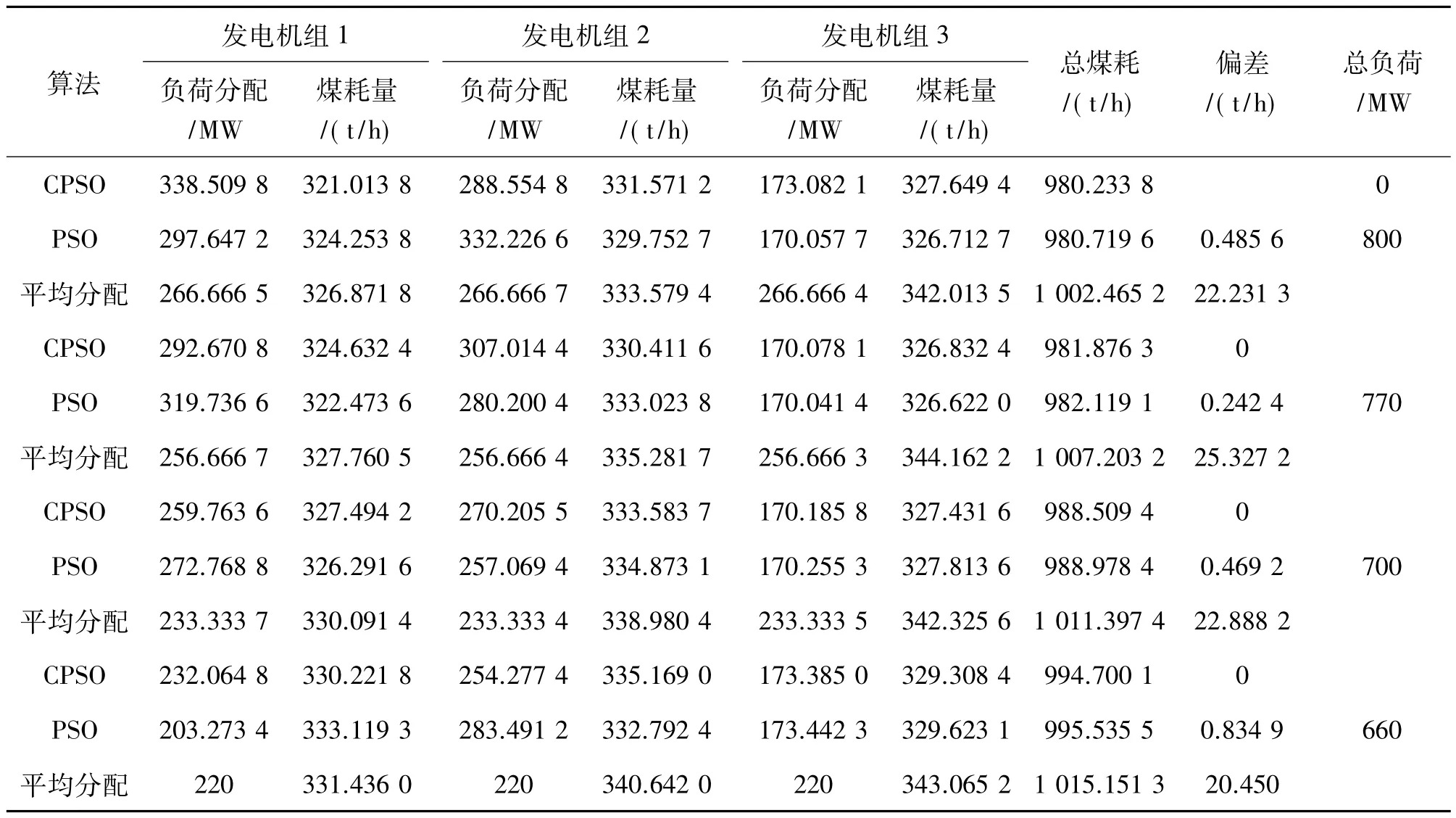
表3 不同总负荷时优化结果(660～800)

表2是在负荷分别为990 MW、900 MW、880 MW时，不同算法的最优负荷分配的结果;表3是在负荷分别为800 MW、770 MW、700 MW和660 MW时，不同算法的最优负荷分配的结果。负荷分配的数据是经算法优化的负荷值，煤耗量的数据是对应负荷所耗的供电煤耗，偏差指的是以混沌粒子群优化所为基准的总煤耗偏差值。

根据表2和表3中的偏差值可发现，虽然混沌现象是一种存在于自然界的非线性现象，但却隐含着规律性，并能在一定范围内按其自身规律重复遍历所有状态。因此，进入搜索后期，粒子陷入局部最优时，CPSO算法能够通过更换粒子或重新调整算法参数引导粒子逃离局部最优区，而PSO算法仍然停留在局部最优解的区域内。分别就D=990 MW、D=880MW、D=770MW和D=660MW进行比较分析，CPSO可以向全局最优解收敛，特别是在全负荷770 MW，算法迭代20次左右收敛，而粒子群算法在112次收敛性，收敛速度前者优于后者。

4 结论

按照混沌粒子群优化算法求解火电厂机组负荷优化分配，得出以下结论:

(1)考虑电厂的实际阀点效应和负荷平衡约束条件，采取罚函数数学建模法，既可将实际的电厂负荷优化分配问题转化为数学问题，又可将实际约束问题转化为非约束问题，最终求得各机组最优负荷的分配情况。

(2)在经典的等微增率法不能适用对象复杂、能耗方程不满足连续递增为凸函数的情况时，粒子群算法从理论与实践证明切实可行，并凸显了搜索最优解的优势。

(3)相比PSO算法，新的CPSO算法更能跳出局部最优解，收敛于全局最优解。特别在迭代次数相同、总负荷不同时的收敛情况，混沌粒子群收敛于全局最优解的速度更快，较好地弥补了PSO算法容易陷入局部最优点、进化后期收敛速度慢的缺点。

［1］王友，马晓茜，刘翱.自动发电控制下的火电厂厂级负荷优化分配［J］.中国电机工程学报，2008，28(14):103-107.

［2］Huang B，Sun Y，Sun YM，et al.A Hybrid Heuristic Search Algorithm for Scheduling FMSBased on Petri Net Method［J］.International Journal of Advanced Manufacturing System，2010，48(9-12):925-933.

［3］Abido M A.Multiobjective Evolutionary Algorithms for Electric Power Dispatch Problem［J］.IEEE Transactions on Evolutionary Computation，2006，10(3):315-329.

［4］沈鑫，曹敏，高文胜，等.基于半马尔科夫过程的变压器故障率预测及研究［J］.电子器件，2015，38(6):1421-1427.

［5］Kennedy J，Eberhart R C.Particle Swarm Optimization［C］//Proceeding of 1995 IEEE International Conference on Neural Networks，New York，NY，USA，1995:1942-1948.

［6］Behnamian J，Zandieh M，Ghomi SM T F.Due Window Scheduling With Sequence-Dependent Setup on Parallel Machines Using Three Hybrid Metaheuristic Algorithms［J］.International Journal of Ad-vanced Manufacturing Technology，2009，44(7-8):795-808.

［7］Eberhart R C，Shi Y.Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization［C］//Proc 2000 Conf Evolutionary Computation.San Diego，2000:84-88.

［8］Kashan A H，Karimi B，Jenabi M.A Hybrid Genetic Heuristic for Scheduling Parallel Batch Processing Machines With Arbitrary Job Sizes［J］.Computers and Operations Research，2008，35(4):1084-1098.

［9］Wang Lin，Yang Bo，Chen Yuehui.Improving Particle Swarm Optimization Using Multi-Layer Searching Strategy［J］.Information Sciences，2014.

［10］Xiong H H，Zhou M C.Scheduling of Semiconductor Test Facility Via Petri Nets and Hybrid Heuristic Search［J］.IEEE Transaction on Semiconductor Manufacturing，1998，11(3):384-393.

［11］Storn R，Price K.Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces［J］.Journal of Global Optimization，1997，11(4):341-359.

［12］司风琪，顾慧，叶亚兰，等.基于混沌粒子群算法的火电厂厂级负荷在线优化分配［J］.中国电机工程学报，2011，26(31): 103-109.

金洪吉(1982-)，女，汉族，四川广元人，工学学士，讲师，研究方向为电气自动化，chayinr@163.com。

Analysis of Chaotic Particle Swarm Optim ization Algorithm of Optimal Load Distribution in Thermal Power Plant

JIN Hongji*

(Department of Electrical Engineering，Sichuan Vocational College of Information Technology，Guangyuan Sichuan 628017，China)

Thermal power plant，according to the performance of the per unit consumption of optimal load distribution，can directly reduce the plant power consumption，effectively meet the needs of enterprise competition and energy-saving emission reduction.Based on this，the verification of the decision algorithm analysis，considering the constraints of the valve point effect and the actual unit，the generating unit load optimization distribution of penalty function mathematicalmodel is established;combining the chaos optimization algorithm and dynamic inertia weight method and particle swarm optimization algorithm，form amore scientific and effective chaotic particle swarm optimization algorithm;using a power plant 3 units of historical data analysis，coal consumption is the biggest decrease of

0.8 t/h，proved the feasibility of the algorithm.

thermal power plant;optimal load distribution;chaotic-particle swarm optimization;coal consumption characteristics;dynamic weight

C:8230

10.3969/j.issn.1005－9490.2017.01.040

TP273

:A

:1005－9490(2017)01－0212－05

2016-01-13修改日期:2016-03-03