基于斯托克斯数的弯管冲蚀数值模拟
周三平(西安石油大学,西安 710065)
基于斯托克斯数的弯管冲蚀数值模拟
周三平
(西安石油大学,西安 710065)
利用计算流体力学数值模拟软件Fluent,采用DPM模型中的稳态方法和随机轨道模型,进行颗粒的运动轨迹追踪。考虑到离散相对连续相的影响,采用相间耦合方法,基于斯托克斯数(St)进行了一系列颗粒对弯管管壁的冲蚀数值模拟。结果表明:弯管入口直管段,冲蚀速率很小且均匀;在随后的弯管段,颗粒聚集较多,该处冲蚀速率较大;出口直管段,当St<1时,冲蚀情况由弯管外侧沿着管壁逐渐均匀过渡到整个管壁四周,管壁最大冲蚀速率随St的增大而略有增大,但增幅很小。当St>1时,颗粒在内外管壁之间变性跃移,管壁冲蚀呈现不连续的点状冲蚀,管壁最大冲蚀速率随St的增大而略有增大,增幅很小,但明显大于St<1时的最大冲蚀速率。
弯管;冲蚀;数值模拟;斯托克斯数(St);液-固两相流
管道运输具有运输量大、连续平稳、经济快速、安全可靠以及占地少等诸多优点,被广泛用在石油石化等各个生产领域,弯管作为管道运输过程中的一个变向管件,发挥着重要的作用。但是流体中难免会携带固体颗粒,这些颗粒将会冲击和摩擦管道内壁使其产生冲蚀,导致管壁局部变薄甚至泄漏,对管道的正常运行产生潜在的威胁。冲蚀是产生工业部件磨损失效的主要原因[1],在管道运输中弯管的冲蚀尤其严重,有研究表明,弯管处的冲蚀磨损比直管部分的大约严重50倍[2]。因此对弯管处冲蚀进行研究具有重要的意义。
针对弯管的冲蚀问题,国内外众多学者的研究主要集中在以下两个方面:一是通过理论解析和试验研究[3-6]的方法对弯管冲蚀的机理进行研究,多数主要是通过数值模拟[7-20]方法对流体的流速、黏度、粒径和弯管弯曲角度、颗粒冲击角度等参数对冲蚀的影响进行研究;二是通过数值模拟的方法对弯管冲蚀进行研究并改进工艺[21]。
冲蚀主要取决于颗粒与管壁的撞击情况,由颗粒的运动轨迹决定。由于颗粒运动轨迹的影响因素众多,包括流体的黏度、流速、流体特征尺寸、密度、粒径等,研究单个因素对冲蚀的影响,不仅工作量巨大,而且由于因素之间的交互影响,使得研究结果难有说服力,也会造成结果众多,难于应用。为此,本工作引进表征颗粒跟随流体运动能力的准数-斯托克斯数来分析颗粒的运动和冲蚀行为。斯托克斯数是由上述众多影响因素组成的无因次数群,它表示颗粒的动量响应时间和流体的特征时间之比,描述了悬浮在流体中的颗粒行为。利用斯托克斯数不仅能够较好地模拟颗粒在流体中运动情况和冲蚀情况,而且能够极大地减少未知数的个数,减少研究工作量,而且使得研究结果更加简单,使用更加方便。
本工作利用计算流体力学数值模拟软件Fluent,研究了在不同斯托克斯数下颗粒在流体中的运动规律以及颗粒对管壁的冲蚀情况。
1 弯管的几何模型及网格划分
弯管的几何模型如图1所示,直径20 mm,弯曲角度90°,曲率半径30 mm。为了克服入口效应的影响,入口段直管长度取为管径的5倍,即100 mm。考虑到弯管后,颗粒的流动情况比较复杂,出口段直管长度取管径的10倍,即200 mm。

图1 弯管几何模型Fig. 1 Geometrical model of the elbow
采用Workbench中meshing模块,用扫略方法对弯管结构进行完全结构化网格划分,以提高网格的划分质量。为了考虑边界层对模拟结果的影响,在管壁附近进行了网格加密。划分后的总体网格数为156 300个,为了节省篇幅,此处仅示出了部分弯管部分网格,见图2。
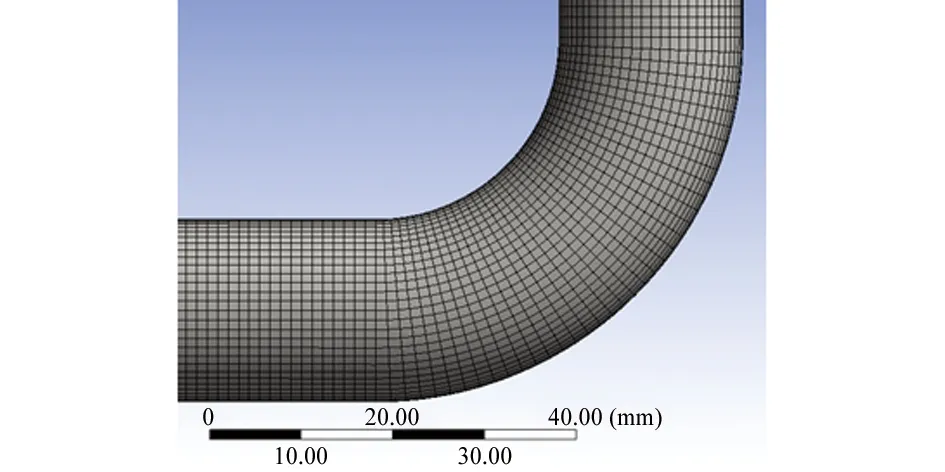
图2 弯管网格划分Fig. 2 Mesh of the elbow
2 弯管冲蚀采用的数学模型
2.1 流体流动数学模型
式中:Sm为流量,ρ为流体密度,p是静压,τij是应力张量,ρgi和Fi分别为i方向上的重力体积力和外部体积力(这里是颗粒相互作用产生的升力)。在此,不考虑重力和外部体积力的影响。
2.2 颗粒相模型
流体中颗粒的体积分率为10%,颗粒相非常稀薄,可以不考虑颗粒与颗粒之间的相互作用、颗粒体积率对连续相的影响等,且这里的入口与出口边界条件确定,在此选用稳态离散项模型(DPM),该模型能够较为清楚地追踪颗粒的运动细节。颗粒的轨道计算采用随机轨道模型,采用相间耦合方法(考虑了离散相对连续相的影响)考察颗粒的分布。
2.3 冲蚀模型
Fluent中冲蚀速率定义如式(3)所示。
式中:mp为颗粒的质量流;C(dp)为颗粒直径的函数C(dp)=1-e-17.387(dp/200-0.025);dp为颗粒直径,在此颗粒尺寸均匀,μm;α为颗粒对壁面的冲击角;f(α)为冲击角的函数;v是颗粒相对于壁面的速率;b(v)是相对速率的函数;Aface为颗粒在壁面的投影面积。
2.4 初始条件和边界条件
在此,连续相流体为水,密度1 000 kg/m3。入口采用速率入口,入口速率为1 m/s,出口采用outflow,壁面施加无滑移固壁的边壁条件。对离散相,颗粒流初始位置在入口面,采用面射流源surface,颗粒的喷入速率等于流体的入口速率(1 m/s)。壁面采用弹射性壁面条件,入口和出口采用逃逸边界条件,颗粒为石英沙,简化为球状颗粒,颗粒密度为2 800 kg/m3,颗粒入口体积分率10%。数值模拟中,连续相湍流模型选用RNG k-ε湍流模型,流体控制方程组采用Quick差分格式,压力速率藕合选择SIMPLE算法。先求解连续相流场,收敛后,创建离散相喷射源,再进行耦合流动求解。
1.3 统计学处理 采用EpiData 3.0建立数据库,实行双人核对数据录入。应用SPSS 24.0软件进行统计分析。呈正态分布或近似正态分布的计量资料以表示,组间比较采用t检验;呈非正态分布的计量资料以M (P25, P75)表示,组间比较采用秩和检验。计数资料以n(%)表示,组间比较采用χ2检验。样本量<40时或频数<1时,采用Fisher确切概率法。检验水准(α)为0.05。
在数值模拟中,通过改变流体黏度和颗粒直径,根据式(4)算得一系列的斯托克斯数St,通过数值模拟得到一系列不同St条件下的冲蚀模拟结果。
式中:u为水的流速;ρp,ρ分别为颗粒与流体的密度;μ为流体的黏度;D为管径。
3 管道内冲蚀数值模拟结果与分析
3.1 湍流模型验证
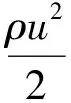
式中:ζ为弯管的局部阻力系数;D为管径,此处D=20 mm;r为管轴线弯曲半径,此处r=30 mm;θ为弯角,此处θ=90°。
3.2 斯托克斯数对弯管管壁冲蚀的影响
为了分析不同的斯托克斯数St对管壁冲蚀的影响,模拟了St=0.012 5、0.025、0.125、0.25、0.5、1、1.25、2、2.5、3、3.5、4、4.5时,90°弯管的冲蚀过程。管壁的冲蚀取决于颗粒的分布情况,限于篇幅,在此只示出了St=0.5、1.25、4时弯管轴截面上的颗粒浓度分布情况(如图3所示)、管壁的颗粒浓度分布情况(如图4所示)以及管壁冲蚀情况(如图5所示)。由图3可见,不同的斯托克斯数条件下,颗粒在弯管入口段内的分布差异较小,由于管中心区域的流速较大,颗粒较均匀地分布在管中心区域偏上的位置,管壁处的速率较小,颗粒的数量相对较少。
与此相对应,体现在冲蚀上就是入口段管壁的冲蚀较小且均匀,如图5所示。差异体现在弯管之后的出口管段。由图3、4可以看出,由于颗粒惯性较大,经过弯管之后,颗粒较多地聚集在弯管外侧管壁。在此之后的出口管段,由图3可见,管中心区域颗粒较少,颗粒沿着管壁由外壁反弹到内壁。但是不同的斯托克斯数,反弹到另一侧的方式不同。根据斯托克斯数的含义,颗粒的斯托克斯数是颗粒的动量响应时间和流体特征时间之比,代表了颗粒惯性力与曳力的相对大小,是表征颗粒运动特性的一个重要无量纲数群。当St<1时,表示颗粒的响应时间很短,颗粒有足够的时间响应周围流体的速率变化,因此颗粒的跟随性较好。由图3(a)、4(a)可见,颗粒由弯管外侧沿着管壁逐渐地均匀过渡到整个管壁四周。在管壁上表现为弯管处外侧管壁颗粒浓度较多,内侧较少,逐渐过渡到到出口处内外基本一致。而当St>1时,颗粒没有足够的时间来响应流体流速的变化,颗粒的惯性力较大,曳力较小,颗粒的运动受流速的变化影响相对较小,颗粒的跟随性较差,在惯性力的作用下,颗粒在内外管壁之间变性跃移,如图3(b)(c)、4(b)(c)所示。图5为相对应斯托克斯数下的管壁冲蚀情况,由图5可见,管壁的冲蚀情况与颗粒的在管壁浓度分布情况吻合,颗粒浓度分布多的地方,冲蚀严重,反之亦然。需要说明的是,这里虽然只示出了St=0.5、1.25、4时的三幅云图,但是St<1的管壁浓度分布情况和冲蚀特征与图3(a)和图4(a)的比较类似,不同的是管壁处颗粒浓度和冲蚀的最大值略有差异,但是差异不大,最大值位置也差不多。这主要是由于St<1时,St差异较小所致。而St>1时,St越大,颗粒的跟随性越差,管壁处颗粒浓度和冲蚀的不太均匀,呈现出不连续的点状冲蚀,最大值位置也随机性较大,位置不固定。
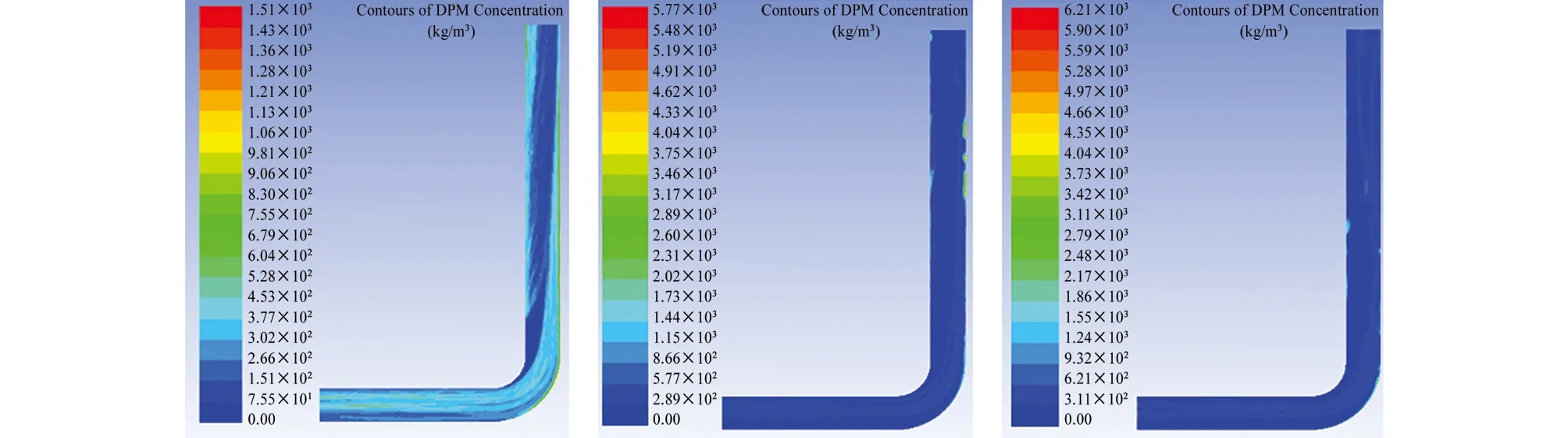
(a) St=0.5 (b) St=1.25 (c) St=4图3 不同斯托克斯数下轴截面的颗粒浓度分布云图Fig. 3 Contours of particle concentration in the axial section with different Stokes numbers

(a) St=0.5 (b) St=1.25 (c) St=4图4 不同斯托克斯数下管壁的颗粒浓度分布云图Fig. 4 Contours of particle concentration of pipe wall with different Stokes numbers

(a) St=0.5 (b) St=1.25 (c) St=4图5 不同斯托克斯数下管壁的冲蚀云图Fig. 5 Contours of erosion of pipe wall with different Stokes numbers
将不同斯托克斯数条件下管壁的最大冲蚀速率绘制成曲线图,如图6所示。由图6可见:当St<1时,管壁最大冲蚀速率随斯托克斯数的增大而略有增大,但是增幅很小,基本稳定。在St=1附近,管壁的冲蚀速率急剧增加。当St>1,管壁最大冲蚀速率随斯托克斯数的变化规律与St<1时的变化规律相同。
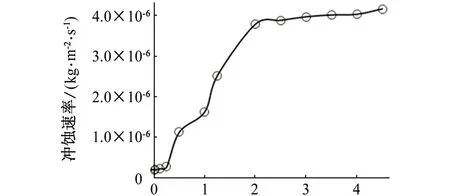
图6 不同斯托克斯数时St最大冲蚀速率Fig. 6 The maximum erosion rates of pipe wall with different stpkes numbers
4 结论
(1) 斯托克斯数不同时,颗粒在弯管入口段内的分布差异较小,颗粒较均匀地分布在管中心区域偏上的位置,管壁处颗粒的数量相对较少。与此相对应,入口段管壁的冲蚀速率较小且均匀。
(2) 弯管稍后,在惯性力的作用下,颗粒较多地聚集在弯管外侧管壁处。该处冲蚀速率较大。
(3) 在弯管之后的出口管段,St<1,颗粒由弯管外侧沿着管壁逐渐地均匀过渡到整个管壁四周。管壁的冲蚀情况与颗粒在管壁的浓度分布情况吻合,颗粒浓度分布多的地方,冲蚀严重,反之亦然。St>1,颗粒独立于流体流动,在惯性力的作用下,颗粒在内外管壁之间变性跃移,管壁呈现不连续的点状冲蚀。
(4)St<1,管壁最大冲蚀速率随斯托克斯数的增大而略有增大,但是增幅很小。在St=1附近,管壁的冲蚀速率急剧增加。当St>1,管壁最大冲蚀速率随斯托克斯数的变化规律与St<1时的情况一样,随St略有增大,但增幅很小。
[1] ALLENCE B. A review of the performance of engineering materials under prevalent tribological and wear situations in south african industries[J]. Tnbology Interational,1996,40(29):105-116.
[2] 陈冠国,褚秀萍,张宏亮,等. 关于冲蚀磨损问题[J]. 河北理工学院学报,1997,4(19):27-31.
[3] 李伟,程建华. 油气线钢弯头腐蚀失效分析[J]. 理化检验-物理分册,2006,42(4):205-209.
[4] 张瑛,申龙涉,王军. 炉管弯头冲蚀失效行为分析[J]. 腐蚀与防护,2009,30(6):132-135.
[5] 梁天霖. 焦化装置加热炉炉管弯头冲刷腐蚀失效分析[J]. 广东化工,2014,41(13):242-243.
[6] 史建强,王印培. 管道弯头穿孔失效分析[J]. 理化检验-物理分册,2007,43(12):633-635.
[7] 王凯,李秀峰,王跃社,等. 液固两相流中固体颗粒对弯管冲蚀破坏的位置预测[J]. 工程热物理学报,2014,35(4):691-694.
[8] 张继信,樊建春,汪彤,等. 压裂液对高压弯管冲蚀作用的数值分析[J]. 润滑与密封,2013,38(4):27-31.
[9] 易卫国,杨谦,李群松. 稀薄颗粒流体对弯管冲蚀的数值模拟[J]. 湖南师范大学自然科学学报,2012,35(5):56-59.
[10] 偶国富,许根富,朱祖超,等. 弯管冲蚀失效流固耦合机理及数值模拟[J]. 机械工程学报,2009,45(11):119-124.
[11] 金浩哲,偶国富,李鹏轩. 基于相似理论的REAC出口弯管冲蚀瞬态特性[J]. 化工学报,2011,62(S2):124-130.
[12] 毛靖儒,柳成文,俞茂铮. 弯管内气动防磨方法的数值检验及其应用[J]. 西安交通大学学报,2000,34(3):17-20.
[13] 李亮,申龙涉,范开峰,等. 弯管中多相流冲刷腐蚀数值模拟[J]. 辽宁石油化工大学学报,2014,34(3):48-52.
[14] 张继军,曹会敏,张少峰. 弯管中液固两相流固粒对壁面磨损的数值模拟[J]. 石油和化工设备,2008,11(1):4-8.
[15] 张少峰,曹会敏,刘燕,等. 弯管中液固两相流及壁面碰撞磨损的数值模拟[J]. 河北工业大学学报,2008,37(3):48-54.
[16] 章本照,沈欣荣,方建农. 矩形截面弯管内气固两相流及对管壁磨损的数值分析[J]. 空气动力学报,1995,13(4):435-441.
[17] 于飞,刘明,王汀,等. 弯头内气-固相流动与管壁磨损特性研究[J]. 工程热物理学报,2015,36(4):796-800.
[18] 刘勇峰,吴明,赵玲,等. 凝析气田集输管道弯管冲刷腐蚀数值计算[J]. 腐蚀与防护,2012,33(2):132-135.
[19] SAMARTH T. Erosion-corrosion failure of a carbon steel pipe elbow-a case study[J]. Corrosion,2009,71(8):852-858.
[20] 梁光川,聂畅,刘奇,等. 基于的输油管道弯头冲蚀分析[J]. 腐蚀与防护,2013,34(9):821-824.
[21] 林建忠,吴法理,余钊圣. 一种减轻固粒对壁面冲蚀磨损的新方法[J]. 摩擦学学报,2003,23(3):231-235.
[22] 高学平. 水力学[M]. 北京:中国建筑工业出版社,2006:143-144.
[23] 李大美,杨小亭. 水力学[M]. 武汉:武汉大学出版社,2004:118-120.
[24] 杨永全,汝树勋,张道成,等. 工程水力学[M]. 北京:中国环境科学出版社,2003:170-171.
欢迎投稿 欢迎订阅 欢迎刊登广告
Numerical Simulation of Erosion of Elbow Based on Stokes Number
ZHOU Sanping
(Xi′an Shiyou University, Xi′an 710065, China)
Using the steady state method in DPM model and the stochastic model of computational fluid dynamics numerical simulation software Fluent, the particle trajectory was tracked. In view of the influence of discrete phase on continuous phase at a series of Stokes number (St), the interphase coupling method was adopted to carry out the numerical simulation of particle erosion-corrosion on the elbow wall. The results show that the erosion rate in the entrance straight section of the elbow is low and uniform and that in the later section just behind the bend of the elbow is relatively large, where the particles are collected. At the exit section of the elbow, whenStis less than 1, the erosion gradually transits from the outside along the pipe wall to the whole wall and the maximum wall erosion rate increases slightly with the increase ofSt, whereas the increment is very small. WhenStis more than 1, particles leap between the inner and outer pipe wall and on the pipe wall discontinuous punctate erosion occurs; the maximum wall erosion rate increases slightly with the increase ofSt, and the increment is very small but significantly larger than that whenStis less than 1.
elbow; erosion; numerical simulation; Stokes number (St); liquid-solid two phase flow
2015-12-08
周三平(1966-),教授,硕士,主要从事化工设备与机械的教学与科研工作,029-88382609,spzhou@xsyu.edu.cn
10.11973/fsyfh-201707016
TG172
B
1005-748X(2017)07-0557-05

