传递系数法在某库岸边坡稳定性研究中的应用
顾明如
(江苏省水利建设工程有限公司,江苏 扬州 225000)
工程勘察
传递系数法在某库岸边坡稳定性研究中的应用
顾明如
(江苏省水利建设工程有限公司,江苏 扬州 225000)
通过对宜宾市金沙江沿岸边坡的工程地质情况进行考察,发现岸坡稳定受金沙江水位升降影响很大。为了研究金沙江下游库岸边坡在各荷载组合工况下的稳定性,以金沙江干流下游左岸两个典型边坡断面为例,采用传递系数法计算了6种不同工况下库岸边坡的稳定系数。结果表明:A-A′断面在6种工况下均处于稳定状态;B-B′断面在工况1~工况4时均处于稳定状态,在工况5时处于基本稳定状态,而在工况6时稳定系数仅有1.008,处于欠稳定状态。计算成果可为后期有关部门设计合理的边坡治理措施提供参考。
金沙江;边坡;传递系数法;稳定系数
1 研究背景
宜宾市安边镇金沙江干流下游的左岸边坡,距上游的向家坝水电站坝址3.50km。由于地理位置的特殊,金沙江安边镇河段均为天然岸坡,根据现场地质调查,库岸边坡不良地质现象较为突出。主要表现为江水位变动及地下水作用造成了该地区岸坡坍塌后退进而产生岸坡再造。岸坡因水位消落和江水冲刷淘蚀容易造成局部滑坡,主要分布于松散堆积物的岸坡。坡脚基岩岩体在江水冲刷淘蚀作用下形成的冲刷槽,如图1。
汛期1次洪峰后的江水位骤降,这种由特大暴雨和洪水造成的水位大幅度消落,在岸坡土体内动水压力作用下,不但容易引发部分稳定性较差的边坡滑体产生塌滑,同时也将加剧岸坡线的局部调整。另外,由于金沙江河流坡降较大,水流流速较大,更加剧了对岸坡的冲刷淘蚀作用,尤其河流拐弯的凹岸段,岸坡迎流顶冲对松散堆积物岸坡的破坏非常突出。由于汛期水位变幅较大,水位抬升较快,对岸坡的水文环境仍带来较为复杂的变化。当水位上升以后,岸坡地下水位逐渐抬升,岸坡岩、土体处于饱水状态,岩土体原有结构及其内聚力减弱,抗剪强度降低,造成岸坡岩土体极易产生塌滑变形破坏。当江水位消落时,岩土体受地下水动水压力增加,岸坡稳定性明显降低,易产生滑移破坏[1,2]。

图1 坡脚基岩冲刷槽
因此,有必要对此区域内的不稳定边坡进行评估,以便后期有关部门采取合理的滑坡治理措施。
2 传递系数法
目前,常用的边坡稳定性计算主要有极限平衡法和有限元强度折减法[3-5]。有限元强度折减法是指通过不断降低边坡的安全系数F,折减后的抗剪参数(黏聚力和内摩擦角)不断代入模型进行重复计算,直到模型达到极限并发生贯通破坏,此时边坡发生破坏前的折减值就是边坡的安全系数F。但此法进行折减计算时是将坡体的黏聚力和内摩擦角按同样的系数进行折减,而这与实际情况不符,故在边坡稳定性计算时,强度折减法存在一定理论缺陷,目前大部分岩土有限元软件仍采用此法计算边坡的安全系数。
传统极限平衡法是根据作用于岩土体中潜在破坏面上块体沿破坏面的抗剪力与该块体沿破坏面的剪切力之比,求该块体的稳定性系数,此法理论推导严格,国内相关边坡也采用极限平衡法计算边坡安全系数。传统的极限平衡法包括瑞典法 (亦称作Fellenious法)、简化Janbu法、Bishop简化法、严格Janbu法等。
2.1 传递系数法基本概念
随着极限平衡法的逐步发展,我国工程技术人员创造了一种实用滑坡稳定分析方法——传递系数法[6-8],亦称为不平衡推力传递法。该法具有计算简单的优点,相比传统的圆弧法,传递系数法适应性更强,计算结果也更加准确,并且能够为滑坡治理提供设计推力。因此在水利部门、铁路部门得到了广泛应用,在国家规范和行业规范中都将其列为推荐的计算方法[9-11]。当滑动面为折线形时,滑坡稳定性分析可采用折线滑动法,而不仅限于圆弧滑动。
2.2 传递系数法的基本假设
(1)将滑坡稳定性问题视为二维平面应变问题。(2)边坡滑动力以平行于滑动面的剪应力τ和垂直于滑动面的正应力σ集中作用于滑动面上。
(3)整个加荷过程中,视滑坡体为理想刚体材料,认为其不会发生任何变形,一旦沿滑动面剪应力达到其剪切强度,则滑坡体即开始沿滑动面产生剪切变形。
(4)滑动面破坏服从摩尔-库伦准则。
(5)条块间的作用力合力(剩余下滑力)方向与滑动面倾角一致,剩余下滑力为负值时,则传递的剩余下滑力为零。
(6)沿整个滑动面满足静力的平衡条件,但不满足力矩平衡条件。
2.3 传递系数法计算
计算简图如图2。
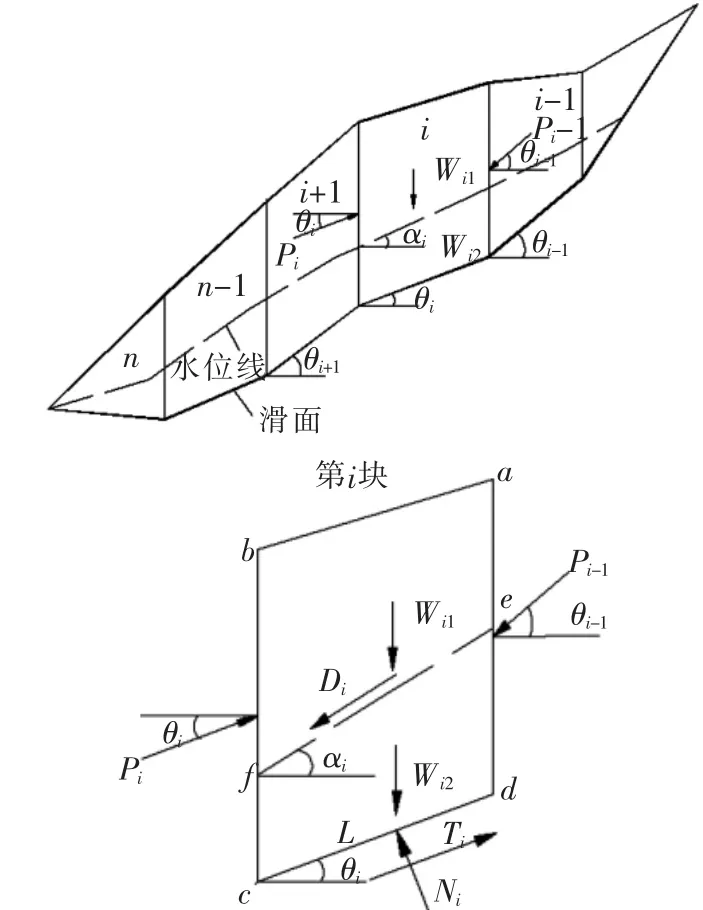
图2 传递系数法计算简图
2.3.1 第i条块的下滑力
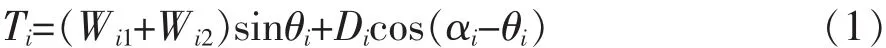
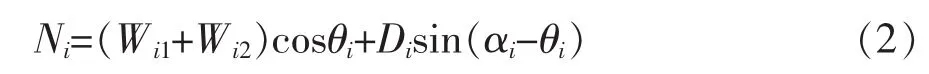
式中 Wi1为第i条块水位线以上天然重量(kN/m);Wi2为第i条块水位线以下的浮重度(kN/m);θi为第i计算条块地面倾角(°),反倾时取负值;Di为渗透压力;αi为第i计算条块地下水流线平均倾角,一般情况下取侵润线倾角与滑面倾角平均值(°),反倾时取负值。
2.3.2 第i块的抗滑力
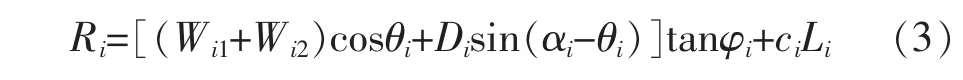
式中 φi为第i计算条块滑带i土的内摩擦角标准值(°);ci为第i计算条块滑动面上岩土体的黏结强度标准值(kPa);Li为第i计算条块滑动面长度 (m);其他符号含义同上式。
其中,条块的天然重量、浮重量分别为:
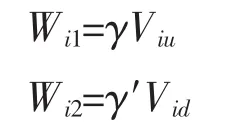
式中 γ为岩土体的天然容重 (kN/m3);γ′为岩土体的浮容重(kN/m3);Viu为第i计算条块单位宽度岩土体的水位线以上的体积(m3/m);Vid为第i计算条块单位宽度岩土体的水位线以下的体积(m3/m)。
渗透压力Di的几何意义:土条中饱浸水面积与水的重度及水力坡降i≈sinαi的乘积,其方向与水流方向一致,与水平向的夹角为αi。计算如式(4):
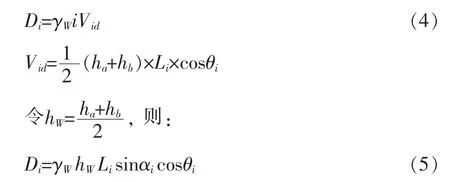
式中 γW为水的容重(kN/m3);hW为第i条块在水位面以下、库水位面以上范围内的高度(m);其他符号含义同上式。
当滑块在水下时,不考虑渗透压力,条块的重量采用浮容重,如图3。
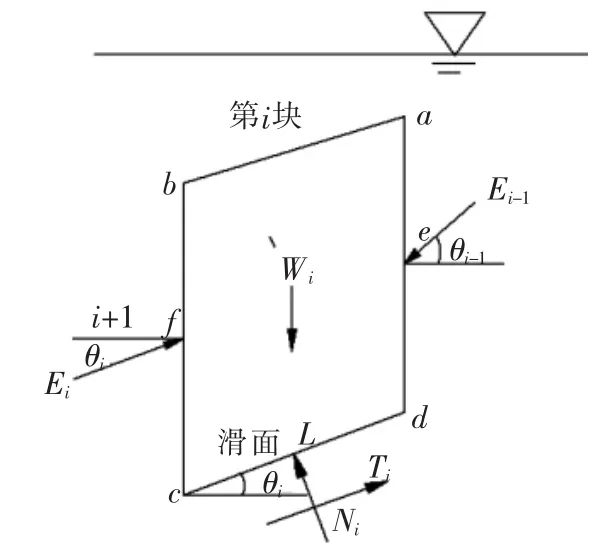
图3 水下条块水压力
第1条块 P1=KT1-R1
第2条块 P2=(KT2-R2)+(KT1-R1)ψ1
第3条块 P3=(KT3-R3)+(KT2-R2)ψ2+(KT1-R1)ψ1ψ2
第4条块 P4=(KT4-R4)+(KT3-R3)ψ1+(KT2-R2)ψ2ψ3+(KT1-R1)ψ1ψ2ψ3
…… ……
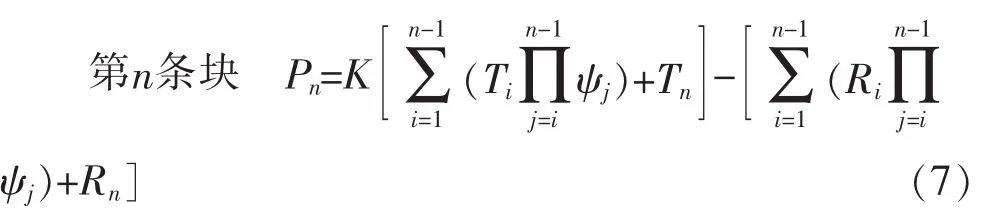
式中 K为防治工程的最小安全系数,对不同级别的防治工程,依据不同的荷载组合确定防治工程的最小安全系数。
当最后条块的滑坡推力Pn=0,K即为滑坡稳定性系数,用Fs表示:
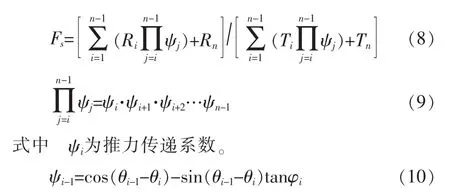
3 计算及分析过程
3.1 计算工况及荷载组合
本工程岸坡后缘有内昆铁路经过,但对滑体基本无影响,且无人类工程活动等其他动荷载,故只考虑土体本身的静止荷载。考虑到岸坡所处的地质结构及金沙江水、暴雨对岸坡的影响,选取勘察期水位(即枯期水位)262.35m、历史洪水位270.0m及设计20年一遇洪水位284.6m为控制水位;选取20年一遇暴雨条件,并且滑动面选取饱和参数计算。
根据国家地震局GB18306—2015《中国地震动参数区划图》,工程区位于Ⅶ度区,地震动峰值加速度值0.1g,稳定性计算时应考虑地震荷载。根据上述条件选取6种典型工况进行稳定性计算,典型工况荷载组合如表1。

表1 典型工况荷载组合

续表1
3.2 计算参数获取
根据三峡库区地灾治理勘察成果资料及同类工程岩土体经验,综合确定滑体稳定性计算参数。确定滑面抗剪强度参数值时,一般以滑体稳定性的宏观地质判断为前提。首先根据地质勘查成果,进行地质判断潜在滑带位置、形态、土质、可能滑面;根据滑坡现状进行反演得出的c,φ值验证;并参考类似工程的经验数据等多方面对比,充分考虑滑坡目前所处的环境、状态及地下水等诱发因素的影响。
因此,根据本工程特点,结合现场钻孔岩芯(孔深5.0~13.3m)取样和试验,提出滑动面的抗剪强度指标及滑体的重度等计算参数,如表2。

表2 岸坡稳定性计算参数
3.3 岸坡稳定性计算结果
由于工程区处于金沙江左岸岸坡,江水位的涨落是直接影响岸坡再造的主要因素,受上游向家坝水电站运行调度影响,江水位涨落频繁,但一般变幅不大,枯水期该江段最低江水位一般高程262.0m,向家坝水电站发电时,水位上涨一般小于1.0m;汛期该段水位上涨较明显,通过对该段岸坡往年洪痕调查,一般汛期高水位高程在270.0m左右。故本次按枯期低水位和汛期高水位作为控制水位进行库岸边坡稳定预测。
库岸边坡计算剖面选取典型且稳定性较差的断面A-A′和B-B′进行分析,断面A-A′坡角22°,断面BB′坡角27°。稳定计算如图4,图5,各工况下库岸边坡的稳定系数计算结果如表3。
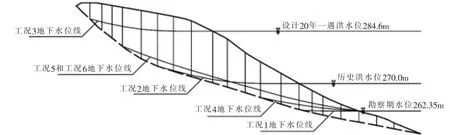
图4 A-A′断面稳定计算
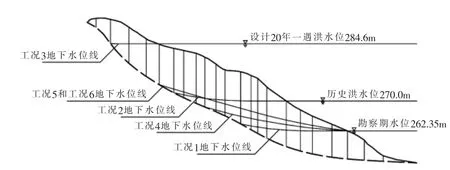
图5 B-B′断面稳定计算
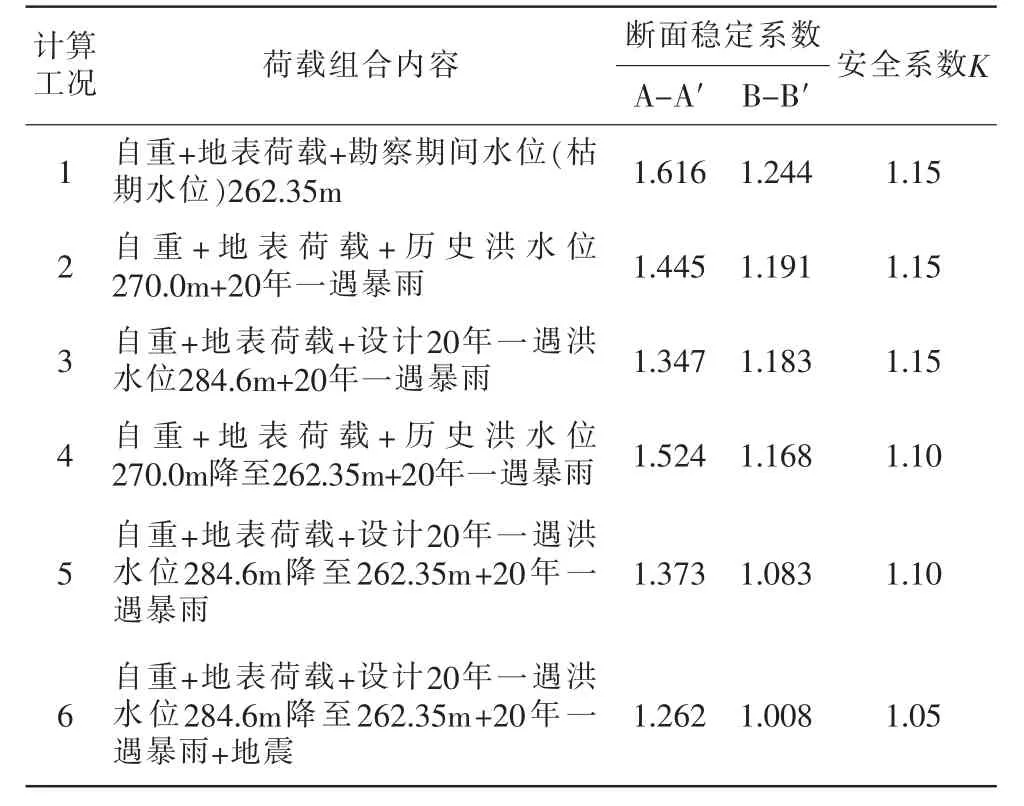
表3 各工况稳定系数计算结果
根据表3计算结果,结合《三峡库区三期地质灾害防治工程地质勘察技术要求》,岸坡稳定性状态按稳定系数分为4级(如表4)。

表4 岸坡稳定状态分级
稳定性计算结果表明:
(1)岸坡A-A′断面在工况1枯期水位时稳定性最好,稳定系数达1.616,在考虑地震和暴雨洪水的工况6时,边坡稳定性最差,但稳定系数为1.262。各种工况下均处于稳定状态;
(2)B-B′断面工况1~工况4均处于稳定状态,工况5处于基本稳定状态,工况6则处于欠稳定状态。故岸坡产生整体滑移性破坏的可能性小,但在进行防洪护岸治理设计时,应结合设计方案复核岸坡的稳定并选择合适的治理方案。
总的来看,本区域内岸坡产生滑移型滑坡的可能性较小。
4 结语
以金沙江干流下游左岸边坡A-A′和B-B′断面为例,采用传递系数法计算了在6种不同荷载组合工况下该库岸边坡的稳定系数,结合《三峡库区三期地质灾害防治工程地质勘察技术要求》,对6种工况下两个边坡断面的稳定性进行分级,最终确定:A-A′断面在6种工况下均处于稳定状态;B-B′断面在工况1~工况4时均处于稳定状态,在工况5时处于基本稳定状态,而在工况6时处于欠稳定状态。综合分析,本研究区域内的岸坡发生整体滑移型滑坡的可能性较小。
[1]郑颖人,陈祖煜,王恭先,等.边坡与滑坡工程治理[M].北京:人民交通出版社,2007.
[2]徐邦栋.滑坡分析与防治[M].北京:中国铁道出版社,2001.
[3]皱丽春,王国进,汤献良,等.复杂高边坡整治理论与工程实践[M].北京:中国水利水电出版社,2006.
[4]时卫民,郑颖人,唐伯明.滑坡稳定性评价方法的探讨[J].岩土力学,2003,24(4):545-548.
[5]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-62.
[6]周海清,刘东升,陈正汉,等.基于传递系数法的滑面指标反算方法的研究[J].地下空间与工程学报,2010,6(6):1161-1167.
[7]沈尧亮,侯殿英.传递系数法的原型与衍生[J].工程勘察,2010,1(S1):477-486.
[8]袁兴平,李珂,张顺斌.差别定义下边坡传递系数法计算差异分析[J].地下空间与工程学报,2014,10(2):347-350.
[9]SL274—2001,碾压式土石坝设计规范[S].
[10]GB50021—2001,岩土工程勘察规范[S].
[11]GB50330—2002,建筑边坡工程技术规范[S].
(责任编辑:尹健婷)
App lication of transfer coefficientmethod on stability research of a bank slope
GU Ming-ru
(Jiangsu Water Conservancy Construction Engineering Co.Ltd.,Yangzhou 225000,China)
Through the investigation of engineering geology of Yibin city Jinsha River along the slope.The slope stability found thathas great influenced by Jinsha Riverwater level fluctuation.In order to study the stability of the lower reaches of the Jinsha River bank slope in the load combination,taking two typical slope section of Jinsha river downstream on the left bank as example,transfer coefficientmethod was used to calculate six different operating conditions of the bank slope stability coefficient.The results show that the A-A′section is in stable state of the six conditions;the B-B′section in no.1~ no.4 working conditions is in stable state,and in stable state at no.5 case,but in no.6 condition with stability coefficient is only 1.008,which is in less stable state.The results can provide a reference for the relevant departments in the design of reasonable slope treatmentmeasures.
Jinsha River;slope;transfer coefficientmethod;stability coefficient
TU457
:A
:1672-9900(2017)04-0012-05
2017-05-15
顾明如(1975-),男(汉族),江苏扬州人,高级工程师,主要从事水利工程施工工作,(Tel)15852990000。

