立方抛物线形断面收缩水深的牛顿迭代公式
陈 诚,金 城,赵程程,王 洁,颜士开
(1.扬州大学 水利与能源动力工程学院,江苏 扬州225009;2.盐城响水船闸管理所,江苏 响水224600;3.常熟市水利工程建设管理处,江苏 常熟 215500)
科研与管理
立方抛物线形断面收缩水深的牛顿迭代公式
陈 诚1,金 城2,赵程程3,王 洁1,颜士开1
(1.扬州大学 水利与能源动力工程学院,江苏 扬州225009;2.盐城响水船闸管理所,江苏 响水224600;3.常熟市水利工程建设管理处,江苏 常熟 215500)
建立立方抛物线形断面收缩水深计算的牛顿迭代公式,误差分析结果表明,其工程适用范围内的最大相对误差绝对值小于6.07×10-5%,平均相对误差绝对值仅小于1.11×10-5%。该迭代公式收敛速度快,且形式较为简捷,大大提高了计算效率,为工程设计及水工设计手册的编制提供参考。
立方抛物线;收缩水深;牛顿迭代;误差分析
随着大型衬砌机的出现和使用,曲线型渠道断面的施工变得越来越容易。由于曲线型渠道断面的拐点较少或没有拐点,因应力集中点导致的裂缝少,故相较于常见的梯型、矩型等断面渠道,其渗漏量较少,同时由于其优良的水力学特性和结构稳定性,近年来得到越来越多的应用[1]。通过计算证明当抛物线断面方程指数n=3.35时,对应的最优水力断面为抛物线类渠道的最优断面型式[2-3],因而立方抛物线形断面是工程中常用的抛物线形断面中水力性能最优的。
泄水建筑物下游的收缩断面水深(contracted water depth)是进行下游水流衔接状态分析、消能工程设计的一个重要水力要素,在工程中应用十分频繁且有较高的计算精度要求。立方抛物线形断面收缩水深计算的实质为一元高次方程的求解,数学上无解析解。现有研究所运用的迭代公式收敛速度慢,计算精度提高不明显[4-6]。本文拟引入牛顿迭代算法,得到一套高速收敛的牛顿迭代公式,且形式较为简捷,可大幅提高计算效率,便于工程设计人员应用。
1 牛顿迭代公式建立
如图1所示,立方抛物线形断面的曲线方程为:

根据水力学原理,由能量守恒方程推得的收缩水深基本方程为:

式中 E0为以收缩断面底部为基准面的过水建筑物上游总水头(m);hc为收缩断面处的水深(m);Q为过水流量(m3/s);g为重力加速度,通常取9.81m/s2;φ为流速系数,一般取0.80~1.00;Ac为收缩断面处的过水断面面积(m2)。

引入无量纲收缩水深x和无量纲参数k:
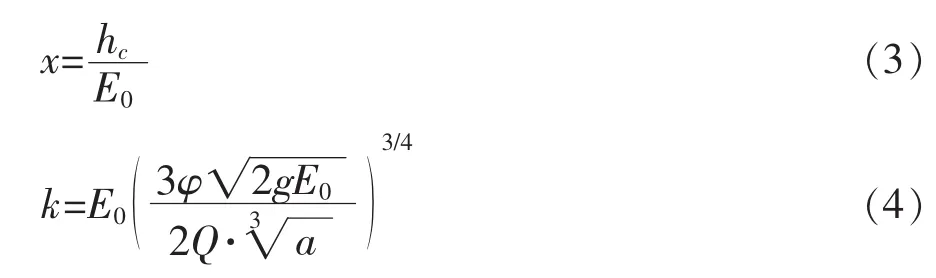
由式(2),式(3),式(4),可推得立方抛物线形断面无量纲收缩水深x的基本方程[4]:

根据式(6),令f(x)=x(1-x)3/8-1/k,则f(x)的一阶导数为:

将f(x),f′(x)代入式(7)并整理,得关于无量纲收缩水深x的牛顿迭代公式:

2 误差分析与精度评价
目前有关水利专家学者共计提出4套基于迭代法的立方抛物线形断面收缩水深计算公式[4-6],均通过引入无量纲参数来计算收缩水深,其中赵延风等[5]公式和滕凯[6]公式是抛物线类断面收缩水深计算的通用公式,将n=3代入得到针对立方抛物线形断面收缩水深计算的公式形式。
各类计算公式如表1。其中λ,ψ,k′为计算过程中引入的中间变量,其他符号意义同前文所述。本文以陈诚等[7]公式作为迭代初值计算公式,在此基础上引入牛顿迭代公式进行计算。为验证牛顿迭代公式的精确性,在[0.01,0.50]区间内以一定步长选取不同的xi,以此作为无量纲收缩水深的精确值x*,将其代入式(4)算得与之相对应的k值,将k作为已知参数代入近似公式,算得无量纲收缩水深的近似值,并根据式(9)计算相对误差δ(保留至小数点后第六位数字),计算结果如图2和表2。

表2 各类公式相对误差

图2 各类公式相对误差分布图(迭代1次)

根据图2和表2,在工程适用范围内,陈诚等[7]公式的最大相对误差绝对值为0.117592%,经过1次迭代之后,最大相对误差绝对值仅小于6.07×10-5%,精度提高近2000倍;以0.0001为步长,计算其在〔0.01,0.50〕区间内的4901个点的相对误差,分别取绝对值之后计算平均值,得平均相对误差绝对值小于1.11×10-5%,精度提高5000倍以上。
运用本文推得的牛顿迭代公式计算立方抛物线形断面的收缩水深,收敛速度和精度远远高于其他各类迭代公式,可大幅提高计算效率。
3 结语
(1)从立方抛物线形断面无量纲收缩水深的基本方程出发,基于牛顿迭代算法建立新的迭代公式,迭代1次之后的相对误差绝对值小于6.07×10-5%,精度较迭代初值计算公式提高103以上,平均相对误差绝对值仅小于1.11×10-5%。相比现有的通过对基本方程进行恒等变形建立的迭代公式,该迭代公式收敛速度快,计算精度高,大幅提高了计算效率,且形式较为简洁。
(2)由于半立方、平方、二分之五次方[8]和立方抛物线形断面的收缩水深基本方程形式类似,该迭代方法均可适用,本文引入的牛顿迭代算法在抛物线类断面收缩水深的计算中具有较好的实用推广价值。
[1]Easa SM.Improved channel cross section with two-segment parabolic sides and horizontal bottom[J].Journal of Irrigation and Drainage Engineering,2009,135(3):357-365.
[2]张丽伟,滕凯.抛物线形断面最优水力参数及方程指数计算方法[J].水利水电科技进展,2014,34(5):65-68.
[3]范子龙,赵明登.幂律形水力最佳断面设计与正常水深计算方法[J].中国农村水利水电,2015(9):157-159.
[4]冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-31,35.
[5]赵延风,王正中,刘计良.抛物线类渠道断面收缩水深的计算通式[J].水力发电学报,2013,32(1):126-131.
[6]代述兵,刘韩生,卞晓卫,等.三种抛物线形断面收缩水深的直接计算公式[J].长江科学院院报,2015,32(9):90-93.
[7]陈诚,龚懿,王洁,等.立方抛物线形断面收缩水深的直接计算研究[J].中国农村水利水电,2017(2):173-175,181.
[8]韩延成,徐征和,高学平,等.二分之五次方抛物线形明渠设计及提高水力特性效果[J].农业工程学报,2017,33(4):131-136.
(责任编辑:尹健婷)
New ton’s iterative formula for contracted water depth in cubic parabolic cross-sections
CHEN Cheng1,JIN Cheng2,ZHAO Cheng-cheng3,WANG Jie1,YAN Shi-kai1
(1.College of Hydraulic,Energy and Power Engineering,Yangzhou University,Yangzhou 225009,China;2.Xiangshui Ship Lock Control Station of Yancheng,Xiangshui224600,China;3.Water Conservancy Project Construction Management Office of Changshu,Changshu 215500,China)
Newton’s iteration formula was established for the calculation of contracted water depth in cubic parabolic crosssections.Results of error analysis indicated that themaximum absolute relative error in practical range was less than 6.07× 10-5%and the average absolute relative error was less than only 1.11×10-5%.The proposed iterative formula has fast convergence rate and brief form,thus perfectly improving the calculating efficiency,which would be used for engineering design practice and for the compilation of hydraulic structure design handbooks.
cubic parabolic;contracted water depth;Newton’s iteration;error analysis
TV131.4
:A
:1672-9900(2017)04-0001-03
2017-04-28
江苏省普通高校研究生科研创新计划项目(KYLX16_1397)
陈 诚(1993-),男(汉族),江苏扬州人,硕士,主要从事农业水资源管理与环境保护研究,(Tel)18168650812。

