莫尔吸量管热水喷泉现象的研究

付伟娟，聂云汉，房振全,马 佳,张嘉俊

(沈阳航空航天大学 a.能源与环境学院;b.理学院，辽宁 沈阳 110136)

莫尔吸量管热水喷泉现象的研究

付伟娟a，聂云汉a，房振全a,马 佳b,张嘉俊b

(沈阳航空航天大学 a.能源与环境学院;b.理学院，辽宁 沈阳 110136)

建立了薄壁大孔口流线型管嘴出流模型，并推导了莫尔吸量管中吸入部分热水后产生喷泉的最大喷射高度表达式. 讨论了吸水体积、热水温度和吸量管直径对最大喷射高度的影响，并分析了影响最大喷射高度的因素. 实验结果表明：热水温度愈高，吸量管直径愈大，喷泉高度愈大. 在影响莫尔吸量管喷泉高度的因素中：流体流动状态对其影响最大，流体在管中与壁面发生碰撞对其的影响程度次之，其次是流体传热对喷射高度的影响，流体本身物性、空气阻力对喷射高度的影响最弱.

热水喷泉；莫尔吸量管；最大喷射高度

1 研究源起

莫尔吸量管热水喷泉问题起源于2016年国际青年物理学家锦标赛(IYPT)赛题中的第7题，原文如下：

Hot water fountain

Partially fill a Mohr pipette with hot water. Cover the top of the pipette with your thumb. Turn the tip upwards and observe the fountain exiting the tip. Investigate the parameters describing the height of the fountain,and optimize them to get the mavimum height.

中文翻译：热水喷泉

用热水部分装填莫尔吸量管. 用大拇指盖住其上端并倒置，可观察到从尖部喷出的水喷泉. 请研究决定水喷泉高度的参量，并改变它们以获得喷泉最大的高度.

2 研究过程

2.1 实验探究

在实验条件方面，基于生活中常见的现象进行合理假设与推演得到热水喷泉现象的系统理论解释. 受实验条件限制，实验过程中采用的是恒温水箱加热并保温水的方法，采用人工实验操作. 为尽量避免或减少人为因素对实验结果的干扰，采取了同一组实验相同实验条件多次测量取其平均值的方法.

实验装置如图1所示，实验主要用到的器材包括：卷尺、恒温水箱、背景布(蓝色)、莫尔吸量管、操作台等. 实验采用视频录制后期分析的方法记录实验数据，并将所得的数据制成表格.

图1 实验装置图

2.2 理论探究

根据对题目的理解与分析，建立如下模型：薄壁孔口出流模型、管嘴出流模型和流线型管嘴出流模型.

建立以上模型的原因：液体在压强差的作用下经过薄壁孔口出流时，由于流线不能突然折转，会形成出口流速，由此建立薄壁孔口出流模型. 而不论薄壁、厚壁，也不论大孔、小孔，孔口出流的公式都可以写成同样的形式，关键在于它们的出流系数各自不同. 而出流系数可由管嘴出流系数查表得到，所以建立管嘴出流模型.

工程上常用的孔口与管嘴[1]有：薄壁孔口、厚壁孔口或外伸管嘴、内伸管嘴、收缩管嘴、扩张管嘴和流线型管嘴. 根据所使用的莫尔吸量管的形状特征，选择建立流线形管嘴模型.

为更好地简化问题建立模型，作如下假设：

1)假设管内被封住的气体为理想气体，进入管内流体为理想流体，且与管壁之间无摩擦；

2)假设热水与管内密封空气传热很快，空气的温度迅速达到与热水相同的温度；

3)假设空气被瞬间加热的同时体积不变；

4)尖嘴距管路开始变化的高度很小，其位能变化对于整体能量变化影响很小，可以忽略.

图2 薄壁孔口出流

对图2中1-1,c-c间流体应用实际流体伯努利方程[2-5]，令α=1，则

(1)

根据连续性方程[1]有

(2)

由此可得

(3)

进而得到吸量管出口流速为

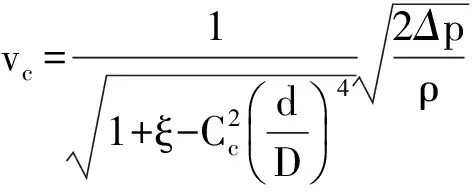
(4)

以50 mL的莫尔吸量管为例，吸量管尖嘴内径d=0.2 cm，吸量管的内径D=1.48 cm，所以此时d并非远小于D，则管道侧壁与孔口外圆周靠近，其收缩程度大为减轻，或者说，莫尔吸量管所属的大孔口的收缩系数较大. 大孔口收缩系数取决于孔口直径与管道直径之比，经验公式为

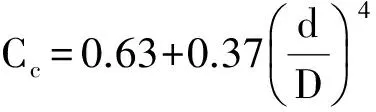
(5)

其中，大孔口的流速系数为

(6)

其中ξ为阻力系数，Cc为收缩系数.

根据假设(1)～(3)，由工程热力学中的理想气体状态方程pV=nRT[6]可知，

(7)

所以有

微生物产生的壳聚糖酶具有多种生物学活性，壳聚糖降解微生物广泛分布于自然界中，微生物通过分泌壳聚糖酶降解壳聚糖以达到需求。壳聚糖酶常常和几丁质酶、几丁质脱乙酰酶和氨基葡萄糖酶等酶的共同使用，来降解回收甲壳类动物的贝壳。壳聚糖是接合真菌细胞壁中主要的结构成分，壳聚糖酶在其细胞壁降解和形态中起着重要作用。

(8)

由(5)和(6)式可知，管嘴出口流速为

(9)

理论推导中所涉及到的流线型管嘴的出流系数等参量可通过查表[1]得到.

(10)

结合(5)和(6)式可求得最大高度为

(11)

2.3 对热水喷泉现象相关影响因素的探究

事先做了几组预实验，大致确认热水温度在40 ℃以上，温度梯度在5 ℃左右，喷泉效果最好. 实验中共有3个变量:热水温度t、吸量管直径D和喷泉高度H. 采用控制变量法：首先控制吸量管直径D不变，探讨热水温度t对于喷泉高度H的影响；再控制热水温度t不变，讨论吸量管直径D对于喷泉高度H的影响.

1)热水温度与喷泉最大高度的关系

表1 喷泉最大喷射高度随热水温度变化实验数据

图3 喷泉最大高度随热水温度的变化

热水温度60 ℃，当吸量管直径D=1.48 cm，吸水体积V水=24 mL时，uH=0.18 cm;当D=0.91 cm,吸水体积V水=6 mL时，uH=0.15 cm;当D=0.71时，吸水体积V水=2 mL时，uH=0.10 cm.

取吸量管直径D=1.48 cm，作出实验高度拟合曲线与理论高度的对比如图4所示.

图4 D=1.48 cm时，实验高度与理论高度对比

通过分析图3与图4可知，喷泉最大喷射高度与热水温度成线性关系，温度越高，喷泉的最大喷射高度越大. 通过传热学[7]相关知识可知，随着温度的升高，莫尔吸量管管内的空气与热水的传热速度加快，传热效率提高，在相同时间内，被加热到可以喷射出吸量管的热水量增多，喷泉到达吸量管管嘴处的初速度变大，即喷射初速度变大，因此，根据能量守恒定律，在忽略空气阻力的情况下，喷泉所能达到的最大喷射高度也就随之增大；而另一方面，水的温度升高使得对气体压强增大，被加热的空气对水做功增加. 因此，水的温度是影响喷泉最大喷射高度的重要因素之一.

2)吸量管直径与喷泉最大高度的关系

测量数据如表2所示，根据表2作图见图5.

表2 喷泉最大喷射高度随吸量管直径变化实验数据

图5 喷泉最大喷射高度随吸量管直径变化

通过图5分析可知，吸量管直径越大，喷泉所能达到的最大喷射高度越大. 吸量管直径不变的情况下，温度升高，最大喷射高度随之升高. 在温度条件相同的情况下，增大吸量管直径可以提高最大喷射高度，但随着直径的再增大，最大喷射高度会趋于稳定.

对此可进行简单的定性解释：在尖嘴直径保持不变的情况下，吸量管直径愈大，尖嘴直径与吸量管直径之间的比值变小，管路的收缩程度增大，莫尔吸量管所属的大孔口的收缩系数增大，进而大孔口的出流速度增大，在忽略空气阻力的情况下，喷泉的喷射高度增大.

2.4 影响因素分析与讨论

1) 流体流动情况的影响

在理论公式推导中，假设液体在吸量管中的流动为层流，但实际流动中可能是湍流，这会影响流体的热量传递效率. 若实际流动中为湍流，则在管壁处形成的速度梯度会比层流大，温度梯度也大，因而在液体流动过程中所造成的热量损失大，影响流体与空气之间的热量传递效率，造成液体传递给空气的动能减少，流体在管嘴处的出口流速变小，所以导致水柱高度会比理论值要小.

2) 流体在管中与壁面发生碰撞的影响

在实际操作中，当温度相对较低时(低于50 ℃)，流体在吸量管倒置过程中，与壁面发生的碰撞十分剧烈，而在此过程中，会造成流体动量的损失，进而造成流体在管嘴处的动能减少，喷出的水柱高度降低.

3) 流体传热对象的影响

在莫尔吸量管喷泉实验中，存在着2部分传热对象：一是流体与管壁之间的传热；一是流体与空气之间的传热. 正因为流体与管壁之间传热的存在，产生了热量损失，导致了整个系统的热量传递效率下降，进而引起了喷出水柱高度的下降.

4) 流体本身物性的影响

在理论公式的推导中，假设流体为理想流体，没有黏度，与壁面之间不存在摩擦. 而在现实情况中，这一假设不成立. 流体与壁面之间存在摩擦，因而流体在流动过程中要消耗一部分能量克服摩擦力做功；流体内部存在黏度，在流动过程中也会对流体的速度产生影响.

5) 空气阻力的影响

在理论公式推导中，忽略流体喷出喷嘴后的空气阻力，利用能量守恒定律可直接求得喷泉高度. 但在实际过程中，喷泉喷出后要受到空气阻力的阻碍作用，这会降低流体的动能，从而影响喷泉高度.

综上分析可得，在影响莫尔吸量管喷泉高度的因素中：流体流动状态对其影响最大，流体在管中与壁面发生碰撞对其的影响程度次之，其次是流体传热对象对喷射高度的影响，流体本身物性、空气阻力对喷射高度的影响最弱.

2.5 后期改进与设想

由于未考虑流体流动情况对于喷泉高度的影响，而只是将问题进行简化，简化为层流；而在实际情况中，湍流的传热效率要比层流高得多，因而通免散失掉的热量也更多，从而对喷泉高度产生的影响更大. 为了更加清楚地研究这一问题，可考虑在吸量管内部装传感器，使之能清楚准确地反映流体的流动情况，进而为问题解决提供思路.

3 结 论

在误差合理的范围内，莫尔吸量管喷泉实验所得到的喷泉高度与热水温度、吸量管直径、尖嘴直径有关. 热水温度愈高，吸量管直径愈大，喷泉高度愈大. 讨论了吸水体积、热水温度、吸量管直径对喷泉最大喷射高度的影响，并得到了喷泉高度与热水温度、吸量管直径之间的理论公式. 利用薄壁大孔口流线型管嘴出流模型与能量守恒定律、对流传热的结合，考虑了流体流动状态、传热对象、与壁面碰撞程度、流体本身物性对于实验结果的影响，实验结果与理论计算基本符合.

[1] 张也影. 流体力学[M]. 2版. 北京：高等教育出版社，1986：239-347.

[2] 赵近芳,王登龙. 大学物理简明教程[M]. 2版. 北京:北京邮电大学出版,2013:67-76.

[3] 李海宝,姜洪喜,张琳,等. 一例关于伯努利方程知识点的教学案例[J]. 物理与工程,2015,25(1):61-64.

[4] 李复. 可压缩流体的伯努利方程[J]. 大学物理,2008,27(8):15-18.

[5] 严导淦. 流体力学中的总流伯努利方程[J]. 物理与工程,2014,24(4):47-53.

[6] 沈维道,童钧耕. 工程热力学[M]. 4版. 北京：高等教育出版社，2015：61-90.

[7] 杨世铭,陶文铨. 传热学[M]. 4版. 北京：高等教育出版社，2015：197-227.

[8] 刘建晓,郑永春,史宫会，等. 热水喷泉现象的理论研究[J]. 物理实验，2016，36(4)：23-26.

[责任编辑：任德香]

Research on the hot water fountain phenomenon of Mohr pipettes

FU Wei-juana, NIE Yun-hana, FANG Zhen-quana, MA Jiab, ZHANG Jia-junb

(a. School of Energy and Environment; b. School of Science,Shenyang Aerospace University, Shenyang 110136, China)

The thin-walled large orifice streamline nozzle outflow model was set up, and the formula of the maximum jet height of hot water fountain of Mohr pipettes was derived. The effect of the water volume, the temperature of the hot water and the diameter of the pipette on the maximum jet height was discussed. Influencing factors on the maximum jet height were analyzed by comparing with the experimental data. The experimental results showed that the higher the hot water temperature and the larger the diameter of the pipette, the greater the height of the fountain. In factors affecting the maximum jet height, the first was fluid flow state, the second was the collision of the fluid with pipette wall, the third was the heat transfer, the influence of the physical properties of the fluid and the air resistance was the weakest.

hot water fountain； Mohr pipette; maximum jet height

2016-11-09；修改日期：2017-01-03

付伟娟(1995-)，女，山东青岛人，沈阳航空航天大学能源与环境学院2014级本科生.

指导教师：马 佳(1984-)，女，辽宁沈阳人，沈阳航空航天大学理学院讲师，博士，研究方向为计算原子分子物理.

O35

A

1005-4642(2017)06-0038-05