一类jerk混沌电路的仿真与设计

王心华，江浩雨，冯娟娟，盛英卓

(兰州大学 a.物理科学与技术学院；b.核科学与技术学院，甘肃 兰州 730000)

一类jerk混沌电路的仿真与设计

王心华a，江浩雨b，冯娟娟a，盛英卓a

(兰州大学 a.物理科学与技术学院；b.核科学与技术学院，甘肃 兰州 730000)

基于jerk系统的基本形式，给出了一类由未确定参量构成的非线性方程，构建了相应的数学模型并进行数值模拟，分析了该系统相图、分岔图及平衡点的性质. 对此系统进行硬件电路实现，得到了与理论计算相符合的混沌吸引子. 研究了电路中电阻变化与系统混沌状态的关系，与分岔图的计算结果基本一致.

混沌；jerk系统；非线性方程；数值模拟

混沌是现代非线性科学的重要分支，其涉及面广，应用前景广阔. 如何利用混沌为人类服务，如何在混沌系统复杂的动力学行为中寻找有序与确定的特性，是当下人们研究的重点[1-2]. 混沌电路是指一类能够产生混沌现象的非线性电路，从混沌的理论分析到实际应用，该类电路起到了至关重要的作用[3-5]. 经过几十年的迅猛发展，混沌电路的研究已获得突破性进展. 因为混沌信号可以作为保密通讯中的加密信号使用，混沌电路已经在保密通信、图像加密等领域得到了广泛的应用[6-9].

通过选取合适的电路元件，构造相应的传递函数，可以有效地产生混沌信号与混沌吸引子[10]. 但是电路的系统方程如何构造，元件如何选取，其与混沌信号的关系如何，则需要进一步探究. 本文基于jerk系统的方程形式，给出了一类由未确定参量构成的非线性方程组，分析了该系统的基本动力学行为，并设计了能够满足该状态方程的模拟电路，进行了硬件实验探究.

1 理论模型

jerk系统是Sprott基于计算机穷举法所提出的三阶自治系统[11-12]，基本形式为

x‴+Ax″+x′=G(x),

(1)

其中G(x)为非线性项，A为常数系数，混沌信号的产生与两者直接相关.

文献[11]中给出了非线性项的几种不同的形式，如绝对值函数、三角函数、阶跃函数、多项式函数等，其中多项式函数在电路中最易实现，所以本文以此为研究对象. 以不含常数项的二次函数为非线性项，故系统方程可改写为

x‴=-a1x″-x′-a2x2-a3x.

(2)

方程(2)中含有3个未定常数系数，如何选取合适的值使之产生混沌状态是需要研究的内容. 对此，以分岔图来研究不同参量所对应的系统状态. 分岔是指非线性微分方程某一参量发生变化时，其解发生突变的临界点行为，通过分析分岔图可以很好地得到系统如何进入混沌[13]. 采用Matlab制作分岔图，具体的算法是首先给定某个参量的取值范围和步长，然后对每次取值时的系统方程进行数值计算，得到相应轨迹，再作一平面x=y截断轨线，平面上点的分布即构成Poincare截面，通过分析截面上散点的分布规律，即可得到系统的运动状态.

首先，令a2=1，a3=1，探究a1对混沌状态的影响，可得分岔图如图1所示. 可见，随着a1从1.0到0.5的改变，系统首先做不动点运动，然后演化为单周期、二周期，最后逐渐由倍周期分岔走向混沌.

同理，a1=0.5，a3=1，以a2为未定参量，可得分岔图如图2所示.

最后，令a1=0.5，a2=1，以a3为未定参量，可得分岔图如图3所示. 从图3中可以看出系统并未出现分岔行为，因此图3已经不能称为严格意义上的分岔图了. 在所选取的a3的取值范围中(a3=0除外)，体系的相空间轨迹与Poincare截面一直都有多个交点，因此系统极有可能处于混沌状态下，其是否处于混沌有待下文的Lyapunov指数求解.

图1 a1为未定参量的分岔图

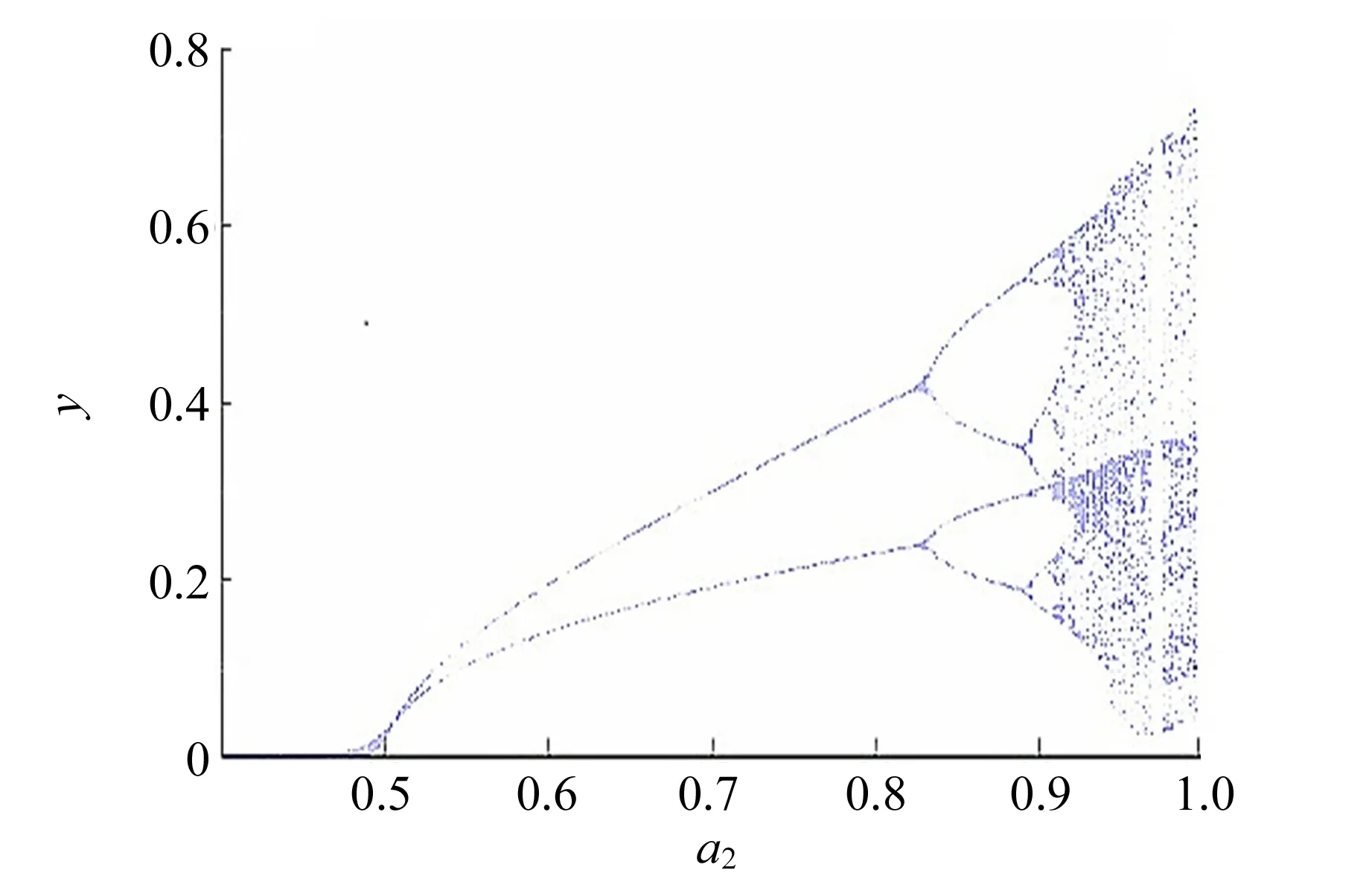
图2 a2为未定参量的分岔图

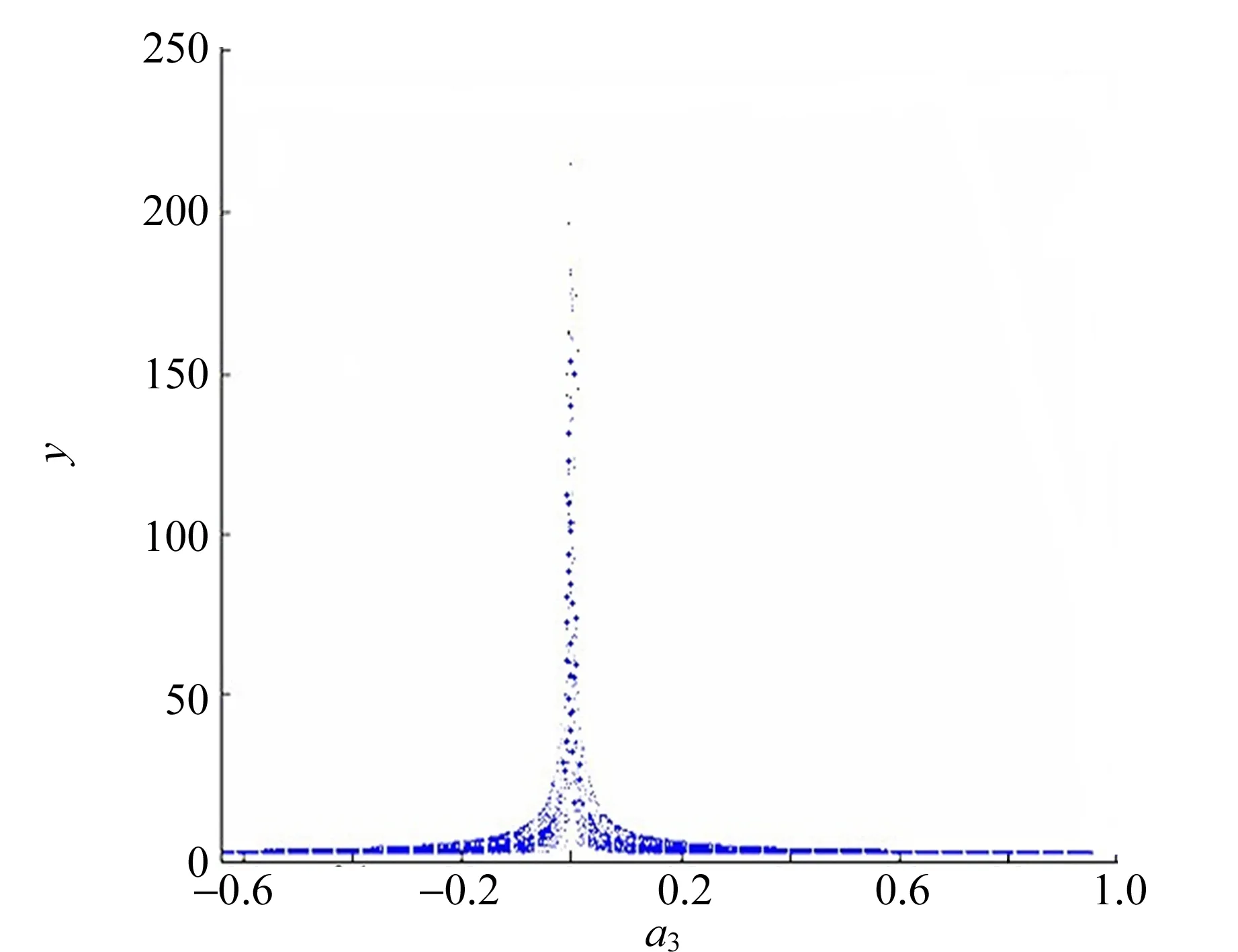
图3 a3为未定参量的分岔图

通过分岔图可以看出，当a1=0.5，a2=1，a3=1时，系统的相空间轨迹与Poincare截面有多个交点，很可能产生混沌. 求解此时系统的3个Lyapunov指数，得到其值分别为：λ1=0.094，λ2=0，λ3=-0.595，满足产生混沌的条件[10]. 并且，在这些参量取值的附近，该方程都处于混沌状态之中. 在实际的硬件操作中，由于电子元件精度等误差的影响，造成实验中模拟的参量不可能与理论值完全一致，如果将未定参量选取为以上的值时，电路系统即使有一定的偏差，只要偏差不是太大，依旧能够产生混沌信号.

对系统的鞍焦平衡点的状态进行分析. 通过变量代换，令：

x=x1,x2=x1′,x3=x2′,

(3)

可得系统的方程

(4)

系统的Jacobin行列式即为

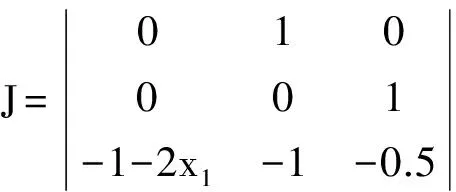
(5)

平衡点P1(0,0,0)对应的特征值为

λ11=r11=-0.803 8，

λ12,13=σ11+iω11=0.151 9±1.105 0i,

指标为2.

平衡点P2(-0.5,0,0)对应的特征值为

λ21=r21=-0.601 5，

λ22,23=σ21+iω21=-0.550 7±1.165 9i,

指标为1.

对于大多数混沌系统来说，指标为1的鞍焦平衡点是连接涡旋之间键带形成的基础，指标为2的鞍点是涡旋运动产生的基础[10,14]. 因此，该系统的相轨迹在平衡点P1(0,0,0)处会形成向外扩展的螺旋状结构.

现在，通过实际的计算来求解方程组. 由于该系统是非线性系统，所以很难求得该方程的解析解，故通过Matlab自带的基于四阶-五阶Runge-Kutta算法的ODE45算法对该方程进行数值求解，得到相应的图像如图4所示. 从相图可以看出，该系统具有1个混沌吸引子，呈单涡旋状结构，与理论分析相符.

(a)x1-t波形图 (b)x2-t波形图 (c)x3-t波形图

(d)x1-x2相图 (e)x1-x3相图 (f)x2-x3相图图4 各参量波形图和相图

2 实 验

为了实现对系统方程的模拟，构造了如图5所示的电路. 电路由3个反向积分器、1个乘法器、3个反向加法器构成，通过回路中电压的变化可实现对方程中参量的模拟，电路中不同部分所对应的参量已在图中标出. 考虑到电路实现的难易程度和成本，积分器、加法器和反相器都采用由集成运算放大器构成的单元电路来实现. 其中，集成运算放大器选用TL084CN，而乘法器可以选择集成乘法器AD633JN四象限集成模拟乘法器，电阻的精度皆为0.1%. 对于积分器来说，其时间常量可以通过控制电阻和电容的大小来改变，而且时间常量仅仅只改变电路中电压变化的整体速率，对于最终所需要得到的相图整体特性并无影响.

图5 电路图

该电路结构简单，非线性器件较少，且没有电感等器件所引入的误差. 通过对x1-(-x2)，x1-x3，(-x2)-x3节点相空间轨迹的测量，可以得到如图6所示的图案. 可见，系统产生奇异吸引子，图像与理论预测相符，即出现了混沌现象.

将R6更换成50 kΩ的电位器，探究电路阻值的改变对混沌状态所造成的影响.R6阻值的改变对应方程(2)中a1参量的改变. 通过实验，得到了如图7所示的图像. 当该R6=10.34 kΩ时，系统由不动点运动进入单周期运动，而由分岔图得到的理论值为10.26 kΩ；当R6=15.43 kΩ时，系统进入二周期运动，理论值为15.79 kΩ；当R6=17.34 kΩ时，系统进入四周期运动，理论值为17.27 kΩ；此后随R6阻值的增大，系统逐渐由多周期运动转变为混沌运动；当R6=25.54 kΩ时，系统进入失真状态，理论值为25.45 kΩ.R6的理论值与实际值之间的微小偏差主要是由于电阻本身0.1%的精度误差造成的.

(a)x1-(-x2) (b)x1-x3 (c)(-x2)-x3

(a)单周期 (b)二周期 (c)四周期

(d)八周期 (e)多周期 (f)混沌

此外，若要观察改变方程(2)中其他参量对整体电路行为造成的影响，可通过改变电路中相应电阻的阻值来实现. 因为对于某个反向加法电路而言，通过调节其电路中电阻的阻值，可以改变输入电压和输出电压的比例. 例如，通过改变R12的阻值，能够调节a3的值；通过改变R9的阻值，能够改变a2的值；等等.

在本文的工作中，只观察到了单涡旋状的混沌吸引子,其是否能够通过调节参量从而得到多涡旋状的复杂行为有待以后验证. 但是需要注意的是，本文中所采用的非线性项为二次函数的jerk方程只是众多jerk方程的一种， jerk方程的非线性部分可以采用多种形式，如绝对值函数、三角函数、阶跃函数、多项式函数等，通过采用不同的函数，能够得到更加复杂的吸引子结构，如双涡漩吸引子[12]，这也是以后有待探究的内容.

3 结束语

设计了基于jerk系统的三阶常系数非线性微分方程的混沌电路，分析了系统的状态与系数取值之间的关系，绘制出了系统的分岔图，清晰直观地体现出系统是如何进入混沌状态的. 分析了系统的鞍点，得出了系统在平衡点附近轨线的变化规律. 构建了对应的硬件实验平台，得到了理论预测的图像，且分析了电阻阻值变化对混沌状态的影响，验证了理论分析的正确性. 本文分析了一类由非确定参量构成的非线性方程系统，该系统拓扑结构简单，电路实现简便，却具有复杂的动力学行为，在保密通信、电子测量等方面具有潜在的应用价值.

[1] 吴文娟. 复杂混沌系统的存在性及动力学特性分析[D]. 天津：南开大学，2010.

[2] 韩伟，徐松源，陈丽红. 工程中混沌现象及混沌应用的研究现状与展望[J]. 电机与控制学报,2001,5(4):251-255.

[3] 周小燕，冯婕. Colpitts混沌振荡电路及其功耗[J]. 物理实验，2016,36(8)：4-7.

[4] 陈菊芳，华影，于东莹. 文氏桥混沌电路的设计与实验[J]. 物理实验，2016,36(8)：8-12.

[5] 陈菊芳，陆静，姜凤怡. 延迟混沌系统投影同步与状态切换的电路实验[J]. 物理实验，2014,34(11)：6-9.

[6] 颜森林. 量子阱激光器混沌相位控制同步以及编码研究[J]. 物理学报，2005,54(3):1098-1104.

[7] 代慧，朱洪雷. 混沌与混沌电路设计方法的可行性研究[J]. 企业技术开发,2010,29(19):24-26.

[8] 阮炯,赵维锐，刘荣颂. 瞬时混沌神经网络的混沌动力学[J]. 应用数学和力学,2003,24(8):874-880.

[9] 刘宇然. 基于光纤信道的双向混沌保密通信的研究[D]. 重庆：西南大学，2012.

[10] 禹思敏，丘水生，林清华. 多涡卷混沌吸引子研究的新结果[J]. 中国科学：技术科学,2003,33(4)：365-374.

[11] Sprott J C. A new class of chaotic circuit [J]. Physics Letters A, 2000,266(1):19-23.

[12] Sprott J C. Simple chaotic systems and circuits [J]. American Journal of Physics, 2000,68(8):758-763.

[13] 郝柏林. 从抛物线谈起[C]//1980年全国非平衡统计物理会议论文集. 大连，1980:43-48.

[14] 张洁. 混沌电路的实验及同步研究[D]. 兰州：西北师范大学,2009.

[责任编辑：任德香]

Simulation and design of a chaotic jerk circuit

WANG Xin-huaa, JIANG Hao-yub, FENG Juan-juana, SHENG Ying-zhuoa

(a. School of Physical Science and Technology; b. School of Nuclear Science and Technology,Lanzhou University, Lanzhou 730000, China)

A family of nonlinear equations based on the jerk circuit was selected and numerically simulated. The phase and bifurcation diagrams of chosen parameters were analyzed, and the properties of the even point were also discussed. An electrical circuit was built to estimate the attractor, and the obtained value agreed remarkably with that of the simulation. Finally, the effect of the resistance of the circuit on the chaotic state was investigated, and the calculation of the bifurcation graph was basically the same.

chaotic state; jerk circuit; nonlinear equation; numerical simulation

2016-08-22；修改日期：2016-12-12

兰州大学“中央高校基本科研业务费专项资金”资助(No.lzujbky-2016-117)

王心华(1979-),男，青海海东人，兰州大学物理科学与技术学院实验师，博士，从事大学物理实验教学及磁性纳米材料研究.

O415.5

A

1005-4642(2017)06-0001-05